Google Code Jam Archive — Farewell Round A problems
Overview
Gardel used to sing in the famous "Volver" tango song that 20 years is nothing. It certainly does not feel that way for Coding Competitions. With these farewell rounds, a marvelous maze reaches the exit. Hopefully it was as entertaining and educational for you to solve it as it was for us to put it together.
For today's rounds we went with a Code Jam-finals setup for everyone: 4 hours, 5 problems, lots of problems with the same score. In this way, each contestant can trace their own path, as you have done throughout our history before.
Round A had all problems at newcomer level with all test sets visible, to align with a Coding Practice With Kick Start round. Round B was also fully visible, but had increasingly harder problems and required some techniques, like a Kick Start round. Rounds C and D had hidden test sets, ad-hoc ideas, some more advanced algorithms and data structures, and included an interactive problem, to cover the full spectrum of the Coding Competitions experience.
We also had appearances from Cody-Jamal, pancakes, names of famous computer scientists, a multi-part problem, I/O problem names, faux references to computer-world terms, and quite a few throwbacks to old problems.
Problems from these rounds will be up for practice until June 1st so you can get a chance at all of them before sign-in is disabled on the site.
Thanks to those of you who could join us today, and to everyone who was around in our long history. It has been amazing. Last words are always hard, so we can borrow from Gardel the ending of "Volver" that does fit the moment: "I save hidden a humble hope, which is all the fortune of my heart."
8 6245 876543 374300 350000 378385 21342 46727 112358
1 2 NA D
1 2 6 *Oo*.d *cNCE*
Cast
Colliding Encoding: Written by Shashwat Badoni. Prepared by Jared Gillespie and Pablo Heiber.
Rainbow Sort: Written by Dmitry Brizhinev. Prepared by Shubham Avasthi.
Illumination Optimization: Written by Melisa Halsband. Prepared by Shaohui Qian.
Untie: Written and prepared by Pablo Heiber.
ASCII Art: Written by Bartosz Kostka. Prepared by Anveshi Shukla.
Collecting Pancakes: Written by Anurag Singh. Prepared by Pranav Gavvaji.
Spacious Sets: Written by Bartosz Kostka. Prepared by Deepanshu Aggarwal.
Intruder Outsmarting: Written by Muskan Garg. Prepared by Pablo Heiber and Saki Okubo.
Railroad Maintenance: Written by Emerson Lucena. Prepared by Mahmoud Ezzat.
Railroad Management: Written by Bintao Sun. Prepared by Yu-Che Cheng.
Game Sort: Part 1: Written by Luis Santiago Re and Pablo Heiber. Prepared by Isaac Arvestad and Luis Santiago Re.
Immunization Operation: Written by Chu-ling Ko. Prepared by Shaohui Qian.
Evolutionary Algorithms: Written by Anurag Singh. Prepared by Vinay Khilwani.
The Decades of Coding Competitions: Written by Ashish Gupta. Prepared by Bakuri Tsutskhashvili.
Game Sort: Part 2: Written by Luis Santiago Re. Prepared by Agustín Gutiérrez and Luis Santiago Re.
Indispensable Overpass: Written by Hsin-Yi Wang. Prepared by Shaohui Qian.
Ring-Preserving Networks: Written by Han-sheng Liu. Prepared by Pablo Heiber.
Hey Google, Drive!: Written by Archie Pusaka. Prepared by Chun-nien Chan.
Old Gold: Written and prepared by Ikumi Hide.
Genetic Sequences: Written and prepared by Max Ward.
Solutions and other problem preparation and review by Abhay Pratap Singh, Abhilash Tayade, Abhishek Saini, Aditya Mishra, Advitiya Brijesh, Agustín Gutiérrez, Akshay Mohan, Alan Lou, Alekh Gupta, Alice Kim, Alicja Kluczek, Alikhan Okas, Aman Singh, Andrey Kuznetsov, Anthony, Antonio Mendez, Anuj Asher, Anveshi Shukla, Arghya Pal, Arjun Sanjeev, Arooshi Verma, Artem Iglikov, Ashutosh Bang, Bakuri Tsutskhashvili, Balganym Tulebayeva, Bartosz Kostka, Chu-ling Ko, Chun-nien Chan, Cristhian Bonilha, Deeksha Kaurav, Deepanshu Aggarwal, Dennis Kormalev, Diksha Saxena, Dragos-Paul Vecerdea, Ekanshi Agrawal, Emerson Lucena, Erick Wong, Gagan Kumar, Han-sheng Liu, Harshada Kumbhare, Harshit Agarwala, Hsin-Yi Wang, Ikumi Hide, Indrajit Sinha, Isaac Arvestad, Jared Gillespie, Jasmine Yan, Jayant Sharma, Ji-Gui Zhang, Jin Gyu Lee, John Dethridge, João Medeiros, Junyang Jiang, Katharine Daly, Kevin Tran, Kuilin Wang, Kushagra Srivastava, Lauren Minchin, Lucas Maciel, Luis Santiago Re, Marina Vasilenko, Mary Yang, Max Ward, Mayank Aharwar, Md Mahbubul Hasan, Mo Luo, Mohamed Yosri Ahmed, Mohammad Abu-Amara, Murilo de Lima, Muskan Garg, Nafis Sadique, Nitish Rai, Nurdaulet Akhanov, Olya Kalitova, Ophelia Doan, Osama Fathy, Pablo Heiber, Pawel Zuczek, Raghul Rajasekar, Rahul Goswami, Raymond Kang, Ritesh Kumar, Rohan Garg, Ruiqing Xiang, Sadia Atique, Sakshi Mittal, Salik Mohammad, Samiksha Gupta, Samriddhi Srivastava, Sanyam Garg, Sara Biavaschi, Sarah Young, Sasha Fedorova, Shadman Protik, Shantam Agarwal, Sharmin Mahzabin, Sharvari Gaikwad, Shashwat Badoni, Shu Wang, Shubham Garg, Surya Upadrasta, Swapnil Gupta, Swapnil Mahajan, Tanveer Muttaqueen, Tarun Khullar, Thomas Tan, Timothy Buzzelli, Tushar Jape, Udbhav Chugh, Ulises Mendez Martinez, Umang Goel, Viktoriia Kovalova, Vinay Khilwani, Vishal Som, William Di Luigi, Yang Xiao, Yang Zheng, Yu-Che Cheng, and Zongxin Wu.
Analysis authors:
- Colliding Encoding: Surya Upadrasta.
- Rainbow Sort: Rakesh Theegala.
- Illumination Optimization: Sarah Young.
- Untie: Pablo Heiber.
- ASCII Art: Raghul Rajasekar.
- Collecting Pancakes: Raghul Rajasekar.
- Spacious Sets: Rakesh Theegala.
- Intruder Outsmarting: Ekanshi Agrawal.
- Railroad Maintenance: Cristhian Bonilha.
- Railroad Management: Emerson Lucena.
- Game Sort: Part 1: Mohamed Yosri Ahmed.
- Immunization Operation: Sadia Atique.
- Evolutionary Algorithms: Krists Boitmanis.
- The Decades of Coding Competitions: Chun-nien Chan.
- Game Sort: Part 2: Agustín Gutiérrez.
- Indispensable Overpass: Arooshi Verma.
- Ring-Preserving Networks: Han-sheng Liu.
- Hey Google, Drive!: Chu-ling Ko.
- Old Gold: Evan Dorundo.
- Genetic Sequences: Max Ward.
A. Colliding Encoding
Problem
Alan just had his first cryptography class in school today. He decided to apply what he
learned and come up with his own cipher. He will map each English letter
from A to Z to a decimal digit $$$0$$$ through $$$9$$$.
He will then try to encode each word to a string consisting of decimal digits by replacing
each letter in the word with its mapped digit.
In his excitement, Alan failed to notice that there are $$$26$$$ letters in the English alphabet and only $$$10$$$ decimal digits. As a result, there might be collisions, that is, pairs of different words whose encoding is the same.
Given a list of $$$\mathbf{N}$$$ words that Alan wants to encode and the mapping that he uses, can you find out if there would be any collisions between words on the list?
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow.
The first line of each test case contains $$$26$$$ decimal digits (integers between
$$$0$$$ and $$$9$$$, inclusve) $$$\mathbf{D_A}, \mathbf{D_B}, \dots, \mathbf{D_Z}$$$, representing the mapping
that Alan uses. A letter $$$\alpha$$$ is mapped to digit $$$\mathbf{D_\alpha}$$$.
The second line of each test case contains $$$\mathbf{N}$$$, the number of words Alan will encode.
The $$$i$$$-th of the last $$$\mathbf{N}$$$ lines contains a string $$$\mathbf{S_i}$$$, representing the
$$$i$$$-th word Alan will encode.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$,
where $$$x$$$ is the test case number (starting from 1) and $$$y$$$ is either YES,
if there is at least one pair of different words from the list whose encoding coincides, and
NO otherwise.
Limits
Time limit: 20 seconds.
Memory limit: 2 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$0 \le \mathbf{D_\alpha} \le 9$$$, for all $$$\alpha$$$.
$$$1 \le $$$ the length of $$$ \mathbf{S_i} \le 10$$$, for all $$$i$$$.
Each character of $$$\mathbf{S_i}$$$ is an uppercase English letter A through Z,
for all $$$i$$$.
$$$\mathbf{S_i} \ne \mathbf{S_j}$$$, for all $$$i \ne j$$$.
Test Set 1 (Visible Verdict)
$$$1 \le \mathbf{N} \le 100$$$.
Test Set 2 (Visible Verdict)
$$$1 \le \mathbf{N} \le 6 \times 10^4$$$.
Sample
2 0 1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 ABC BC BCD CDE 0 1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 CDE DEF EFG
Case #1: NO Case #2: YES
In Sample Case #1, the mapping for A is $$$0$$$, for B is $$$1$$$,
for C is $$$2$$$, for D is $$$3$$$, and for E is $$$3$$$.
With this mapping, ABC is encoded as $$$012$$$, BC is encoded
as $$$12$$$, BCD as $$$123$$$,
and CDE as $$$233$$$. Since all of these encodings are distinct, there
are no collisions.
In Sample Case #2, the mapping for C is $$$2$$$, for D is $$$3$$$,
for E is $$$3$$$, for F is $$$3$$$, and for G is $$$3$$$.
With this mapping, CDE is encoded as $$$233$$$, DEF as $$$333$$$,
and EFG as $$$333$$$.
Since the encoding for DEF and EFG is
the same, there is a collision.
B. Illumination Optimization
Problem
Onyaomale is leading a project to exchange the lightbulbs from street lights along a freeway from incandescent ones to LED lightbulbs that are both more energy-efficient and powerful. She started by taking all the old incandescent lightbulbs out, and is now focused on installing the new LED ones. Because the new lightbulbs are more powerful, Onyaomale thinks it is possible that some street lights are not necessary and she can save even more energy by not using them.
We model the freeway as a straight line measuring $$$\mathbf{M}$$$ meters that goes from west to east. The $$$x$$$-th meter is a point that is $$$x$$$ meters to the east of the western end of the freeway. If a street light is located at the $$$x$$$-th meter, and a lightbulb with an illumination radius of $$$\mathbf{R}$$$ meters is installed on it, then the street light illuminates the segment of freeway starting at the $$$\max(0, x - \mathbf{R})$$$-th meter and ending at the $$$\min(\mathbf{M}, x + \mathbf{R})$$$-th meter, inclusive. Onyaomale needs to install lightbulbs in such a way that every point of the freeway is illuminated by at least one of them. Notice that this includes illuminating points that are not an integer number of meters away from the freeway endpoints. Street lights that are left without a lightbulb do not illuminate anything.
Given the length of the freeway in meters $$$\mathbf{M}$$$, the illumination radius of the new lightbulbs $$$\mathbf{R}$$$ and the locations of all street lights, find the minimum number of lightbulbs Onyaomale needs to install to illuminate the whole freeway, or report that it is impossible to do so.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow. Each test case consists of two lines. The first line contains three integers $$$\mathbf{M}$$$, $$$\mathbf{R}$$$, and $$$\mathbf{N}$$$: the length, in meters, of the freeway, the illumination radius, in meters, of the lightbulbs and the number of street lights, respectively. The second line of a test case contains $$$\mathbf{N}$$$ sorted integers $$$\mathbf{X_1}, \mathbf{X_2}, \dots, \mathbf{X_N}$$$ representing the meters of the freeway where street lights are located.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$,
where $$$x$$$ is the test case number (starting from 1) and $$$y$$$ is the minimum number
of lightbulbs Onyaomale needs to install to illuminate the whole freeway, if it is possible.
If there is no way to illuminate the entire freeway using the current street lights, $$$y$$$
should be IMPOSSIBLE instead.
Limits
Time limit: 10 seconds.
Memory limit: 2 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$1 \le \mathbf{M} \le 10^9$$$.
$$$1 \le \mathbf{R} \le 10^9$$$.
$$$0 \le \mathbf{X_1}$$$.
$$$\mathbf{X_i} \lt \mathbf{X_{i+1}}$$$, for all $$$i$$$.
$$$\mathbf{X_N} \le \mathbf{M}$$$.
Test Set 1 (Visible Verdict)
$$$1 \le \mathbf{N} \le 10$$$.
Test Set 2 (Visible Verdict)
$$$1 \le \mathbf{N} \le 10^5$$$.
Sample
3 10 3 3 2 7 9 10 2 3 2 7 9 10 2 4 2 3 7 9
Case #1: 2 Case #2: IMPOSSIBLE Case #3: 4
In Sample Case #1, Onyaomale can illuminate the entire freeway by placing bulbs in the western-most and middle street lights only, leaving the eastern-most one unused. With these two lights covering $$$[0, 5]$$$ and $$$[4, 10]$$$, the entire freeway ($$$[0, 10]$$$) is illuminated.
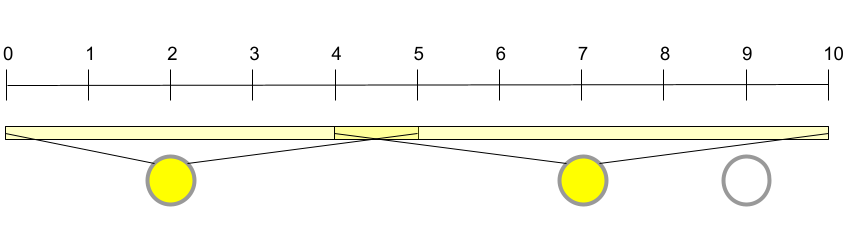
In Sample Case #2, Onyaomale has the same configuration as in Sample Case #1, but with weaker lightbulbs. In this case, there is no way for her to illuminate the entire freeway. In particular, even if all the street lights are lit, the middle point between the $$$4$$$-th and $$$5$$$-th meters would still not be illuminated.
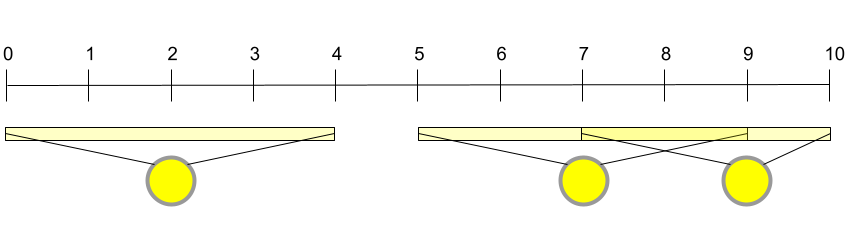
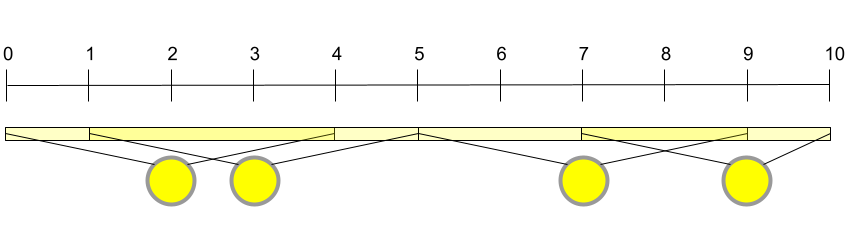
For Sample Case #3 Onyaomale has an additional street light at the $$$3$$$-th meter, compared to Sample Case #2, while all other conditions are the same. In this case, installing a lightbulb in every street light is the only way to have the entire freeway illuminated.
C. Rainbow Sort
Problem
Your friend Charles gives you a challenge. He puts $$$\mathbf{N}$$$ cards on a table and arranges them in a line in an order that he chooses. Each card has a single color, and each color can be on one or more cards.
Charles then asks you to write a positive integer on each card without altering his chosen order such that:
- The integers you write appear in non-decreasing order when cards are read from left to right.
- Cards of the same color have the same integer written on them.
- Cards of different colors have different integers written on them.
Finally, Charles wants you to order the colors in increasing order of written integer. For example, if blue cards have a $$$2$$$, red cards have a $$$5$$$, and green cards have a $$$3$$$, the color order would be blue, green, red.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow.
Each test case begins with a line containing the integer $$$\mathbf{N}$$$. The next line contains $$$\mathbf{N}$$$ integers, $$$\mathbf{S_1}$$$, $$$\mathbf{S_2}$$$, $$$\dots$$$, $$$\mathbf{S_N}$$$, where $$$\mathbf{S_i}$$$ represents the color of the $$$i$$$-th card from the left.
Output
For each test case, output one line containing
Case #$$$x$$$: $$$y$$$, where $$$x$$$ is the test case number
(starting from 1) and $$$y$$$ is the set of colors, once each, listed in the requested order.
If it is impossible to write integers in the given cards while adhering to all
the rules, $$$y$$$ must be IMPOSSIBLE instead.
Limits
Time limit: 20 seconds.
Memory limit: 2 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$1 \le \mathbf{S_i} \le 10^5$$$, for all $$$i$$$.
Test Set 1 (Visible Verdict)
$$$1 \le \mathbf{N} \le 10$$$.
Test Set 2 (Visible Verdict)
$$$1 \le \mathbf{N} \le 10^5$$$.
Sample
2 4 3 8 8 2 5 3 8 2 2 8
Case #1: 3 8 2 Case #2: IMPOSSIBLE
In Sample Case #1, there are $$$3$$$ different colors on $$$4$$$ cards. One possible solution is to write the following integers, in order: $$$1$$$, $$$2$$$, $$$2$$$, and $$$3$$$. Notice that the same integer ($$$2$$$) is written on both cards of color $$$8$$$. Then, the order of the colors is $$$3$$$, $$$8$$$, $$$2$$$.
In Sample Case #2, let $$$c_8$$$ and $$$c_2$$$ be the integers written in cards of color $$$8$$$ and $$$2$$$, respectively. If $$$c_2 \gt c_8$$$ then the rightmost two cards would not have their integers in non-decreasing order. If $$$c_2 \lt c_8$$$ that would happen to the second and third card from the left. Finally, $$$c_8 = c_2$$$ is forbidden by one of the rules. Therefore, there is no valid way of writing the integers in this case.
D. ASCII Art
Problem
Cody-Jamal has heard about generative artificial intelligence producing art. He is excited about the new art opportunities, but also worried about human-created art being displaced. He thought a good compromise would be to use computers to create art that humans simply cannot.
Since Cody-Jamal is just beginning at computer-generated art, he started simple. He wants to create an immense string that shows the English alphabet in a doubly-repeated way, to represent its ubiquity and permanence.
Cody-Jamal wrote the following program:
for i = 1 to 1e100:
for letter = A to Z:
print letter i times
Here 1e100 represents the integer $$$10^{100}$$$. For example:
- When $$$i=1$$$, the program prints
ABCD....XYZ. - When $$$i=2$$$, the program prints
AABBCC...XXYYZZ. - When $$$i=3$$$, the program prints
AAABBBCCC...XXXYYYZZZ.
Of course, Cody-Jamal's program takes a long time to finish. Can you help him know what the $$$\mathbf{N}$$$-th printed letter will be without waiting for it to be printed?
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test
cases follow.
Each test case consists of a single line with an integer $$$\mathbf{N}$$$.
Output
For each test case, output one line containing
Case #$$$x$$$: $$$y$$$, where $$$x$$$ is the test case number
(starting from 1) and $$$y$$$ is the $$$\mathbf{N}$$$-th character printed by Cody-Jamal's
program.
Limits
Time limit: 20 seconds.
Memory limit: 2 GB.
$$$1 \le \mathbf{T} \le 100$$$.
Test Set 1 (Visible Verdict)
$$$1 \le \mathbf{N} \le 10^6$$$.
Test Set 2 (Visible Verdict)
$$$1 \le \mathbf{N} \le 10^{12}$$$.
Sample
2 5 31
Case #1: E Case #2: C
The first $$$35$$$ letters printed by Cody-Jamal's program are
ABCDEFGHIJKLMNOPQRSTUVWXYZAABBCCDDE.... Therefore, the $$$5$$$th
printed character is E and the $$$31$$$st is C.
E. Untie
Problem
A group of people are sitting in a circle, playing a special version of rock, paper, scissors. In this game, each person chooses rock, paper, or scissors in secret and then everyone reveals their choice to everyone else. Each person then compares their selection to their two neighbors, and can win, lose, or tie against each of them independently. The only way to tie is when both people make the same choice.
You want to make it so that no game is a tie. For each player, you can let them keep their choice, or you can ask them to change to any of the other two options (you choose to which one). What is the minimum number of people you need to request a change from to ensure that there are no ties between neighbors after those changes are made?
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ lines follow.
Each line represents a test case and contains a string $$$\mathbf{C}$$$. The $$$i$$$-th character of $$$\mathbf{C}$$$
represents the original choice of the $$$i$$$-th person in clockwise order using
an uppercase R to mean rock, an uppercase P to mean paper,
and an uppercase S to mean scissors.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$,
where $$$x$$$ is the test case number (starting from 1) and $$$y$$$ is the minimum number
of changes that are required such that no two neighbors end up with the same choice.
Limits
Time limit: 10 seconds.
Memory limit: 2 GB.
$$$1 \le \mathbf{T} \le 100$$$.
Each character of $$$\mathbf{C}$$$ is either an uppercase R, an uppercase P, or
an uppercase S.
Test Set 1 (Visible Verdict)
$$$3 \le$$$ the length of $$$\mathbf{C} \le 10$$$.
Test Set 2 (Visible Verdict)
$$$3 \le$$$ the length of $$$\mathbf{C} \le 1000$$$.
Sample
3 PRSSP RRRRRRR RSPRPSPRS
Case #1: 2 Case #2: 4 Case #3: 0
In Sample Case #1, there is a pair of neighbors that both chose paper (the first
and last character of the input) and another pair that
both chose scissors. Therefore, we need at least two changes. One way of doing it with two
changes is to change the leftmost paper to scissors and the rightmost scissors to rock, to
obtain SRSRP.
In Sample Case #2, all $$$7$$$ participants chose rock. If we change at most $$$3$$$ selections,
there will be at least $$$4$$$ remaining rocks, and at least two of them will be neighbors.
Therefore, the minimum number of changes is at least $$$4$$$. One way to achieve exactly $$$4$$$
is to get PRSRPRS.
In Sample Case #3, no pair of neighbors tied, so no changes are needed.
Analysis — A. Colliding Encoding
Test set 1
For the small test set, we compare each word encoding with the other words encodings. If
any of the two encodings are equal then the answer is YES. Otherwise, the answer is
NO. The time complexity for encoding all the words is $$$O(L)$$$ where $$$L$$$ is
the sum of the lengths of the given $$$\mathbf{N}$$$ words. Since the length of a word is at most $$$10$$$,
$$$O(L)$$$ can be written as $$$O(\mathbf{N})$$$. Therefore overall time complexity for this solution
is $$$O(\mathbf{N}^2)$$$ which is sufficient for the small test set.
Test set 2
The above solution is not suitable for the large test set. Instead of comparing each pair of encoded words, we can calculate encoding for each word and then use hashing or sorting algorithms to check if any two encodings are equal.
Method 1
Hashing: We use a hash table to store the encodings. Before inserting an
encoding of a word, we check if it already exists there. If it already exists then the answer is
YES. If we had to insert all the words encodings then all are unique and the answer
is NO. The time complexity for encoding all the words is $$$O(\mathbf{N})$$$. The time
complexity for checking all the words in the hash table is also $$$O(\mathbf{N})$$$. The overall time
complexity of this solution is $$$O(\mathbf{N})$$$ which is sufficient for the large test set.
Sample Code(C++)
string anyCollisions(vector<string> words, vector<int> encoding) {
unordered_set<string> encoded_words;
for(int i = 0; i < words.size(); i++) {
string encoded_word;
// Calculate the encoding for the word and store in encoded_word.
if (encoded_words.contains(encoded_word)) {
return "YES";
}
encoded_words.insert(encoded_word);
}
// If we reach here then there are no collisions.
return "NO";
}
Method 2
Sorting: We store the encoding for each word in an array and sort them. If any two adjacent
encodings are equal then the answer is YES. Otherwise, the answer is NO.
The time complexity for encoding all the words is $$$O(\mathbf{N})$$$ and for sorting it is
$$$O(\mathbf{N}\log\mathbf{N})$$$. The overall time complexity of this solution is $$$O(\mathbf{N}\log\mathbf{N})$$$ which is
sufficient for the large test set.
Sample Code(C++)
string anyCollisions(vector<string> words, vector<int> encoding) {
vector<string> encoded_words;
for(int i = 0; i < words.size(); i++) {
string encoded_word;
// Calculate the encoding for the word and store in encoded_word.
encoded_words.add(encoded_word);
}
encoded_words.sort();
for(int i = 0; i < encoded_words.size() - 1; i++) {
if (encoded_words[i] == encoded_words[i+1]) {
return "YES";
}
}
// If we reach here then there are no collisions.
return "NO";
}
Analysis — B. Illumination Optimization
Test Set 1
For Test Set 1, we can use brute force and check all possible combinations of street light locations. For each combination, we need to check if it covers the entire freeway, and if it does, we add it to the list of candidates. We then return the combination which uses the least number of street lights. This will take $$$O(\mathbf{N} \times 2^\mathbf{N})$$$.
Test Set 2
For the Test Set 2, there are two observations we can make:
Since the radius is the same, this ensures that if the left point of a street light starts before the left point of another street light, it must also end before that street light. Since the light locations are given in sorted order, we will be able to iterate through them from left to right without skipping any street lights. Our ultimate goal is to find the minimum number of street lights where the freeway is lit up. Thus we can iterate through the given street light locations from left to right, and when deciding which street light to use, we take the rightmost light that also is able to cover all area (on the left) that has not been covered yet. This greedy strategy is always an optimal one, because it always leaves the rest of the uncovered areas of the street to be as small as possible.
To do this, we can keep a counter of how many street lights we used, as well as a variable to keep track of what area has been covered so far. We can do this by saving a variable $$$curr\_rightmost\_covered$$$ for what is covered so far. Specifically, the range $$$[0, curr\_rightmost\_covered]$$$ denotes what is already covered. Everytime we see a new street light at $$$\mathbf{X_i}$$$, we check that it does not leave a gap in the uncovered area by checking if $$$\mathbf{X_i} - \mathbf{R} \le curr\_rightmost\_covered$$$. If it does leave a gap, then it means that no street light can cover that gap, so the answer is impossible. Otherwise, we check the next street light after it, $$$\mathbf{X_{i+1}}$$$, to see whether that one also leaves no gap. If so, then we would prefer to use $$$\mathbf{X_{i+1}}$$$ instead of $$$\mathbf{X_{i}}$$$ and so forth. We will need to keep checking the next street light until we see one that leaves a gap $$$\mathbf{X_{k+1}}$$$. If the next street light $$$\mathbf{X_{k+1}}$$$ does leave a gap, that means we must take $$$\mathbf{X_{k}}$$$. In that case, we update $$$curr\_rightmost\_covered$$$ to $$$\mathbf{X_{k}} + \mathbf{R}$$$ where $$$\mathbf{X_k}$$$ is the rightmost street light that leaves no gap.
When the entire freeway is covered, we can stop and return the count of how many streets lights we used. The time complexity of this solution is $$$O(\mathbf{N})$$$ for each test case.
Analysis — C. Rainbow Sort
Test Set 1
In this test set, since $$$\mathbf{N}$$$ is very small, we can try all possible orderings
of unique values of colours and use their indices in these orderings to build candidate A arrays and
find one non-decreasing A from them.
Find all the unique values of $$$\mathbf{S}$$$ using a hash set in $$$O(\mathbf{N})$$$ time. Let
$$$M$$$ be the array holding the unique values.
Find all the permutations of $$$M$$$. For each permutation $$$P$$$ of $$$M$$$,
follow the below logic to create A.
Initialize a hash map $$$X$$$. For each $$$P_i$$$, assign $$$X[P_i] = i$$$. Iterate
through $$$\mathbf{S}$$$ and for each $$$\mathbf{S_i}$$$, assign A$$$[i] =
X[\mathbf{S_i}]$$$. Once A is constructed, we can easily check whether
A is non-decreasing by iterating through the array.
Return IMPOSSIBLE if none of the A arrays is
non-decreasing, else return one of them as the answer. For each permutation,
we take $$$O(\mathbf{N})$$$ time to check whether the array A is non-
decreasing. Since there are $$$O(\mathbf{N}!)$$$ such permutations, the overall
complexity of this solution is $$$O(\mathbf{N}! \times \mathbf{N})$$$.
Test Set 2
The previous algorithm would be too slow for Test Set 2, so we must find a more efficient solution.
For cards to have a possible valid A array, we can conjecture that
cards with the same value should be consecutive to each other, i.e., not
separated by another card of a different value.
By way of contradiction, let us suppose our above conjecture is incorrect i.e., at least one card is present with
a different number between two cards with same value.
Let $$$\mathbf{S_i}$$$, $$$\mathbf{S}_j$$$, $$$\mathbf{S}_k$$$ be three values in S such that $$$ i
\lt j \lt k$$$ and $$$\mathbf{S_i} = \mathbf{S}_k \ne \mathbf{S}_j $$$. Hence
A$$$[i] = $$$A$$$[k]
\ne$$$A$$$[j]$$$.
Since $$$\mathbf{S_i} \ne \mathbf{S}_j$$$, A$$$[i] \lt
$$$A$$$[j]$$$.
Similarly, since $$$\mathbf{S}_j \ne \mathbf{S}_k$$$,
A$$$[j] \lt $$$A$$$[k]$$$.
Hence, A$$$[i] \lt $$$A$$$[k]$$$ which is
contradictory.
So cards with the same values should be consecutive to each other.
It follows from the above observation that we only need to consider unique
values of $$$\mathbf{S}$$$. For simplicity, let $$$K$$$ be the array after removing
consecutive duplicates while keeping one instance of one unique value in $$$\mathbf{S}$$$ and
also keeping the order of unique elements same. Let $$$L$$$ be the array such
that $$$L_i$$$ is the index position of $$$\mathbf{S_i}$$$ in $$$K$$$. We can easily
see that $$$L$$$ is a non-decreasing array and the mapping between $$$\mathbf{S}$$$ and
$$$L$$$ is one to one.
Initialize an A array and an empty hash set to store elements
of $$$\mathbf{S}$$$ seen while iterating. Iterate through $$$\mathbf{S}$$$ from left to right and for
each $$$\mathbf{S_i}$$$, find if the element appeared before in the list i.e., if the
element is present in the hash set.
If the element is not present, then insert the element into the hash set and
A array and continue iterating.
If the element is present in the hash set and it is equal to the previous element in
$$$\mathbf{S}$$$ then continue iterating else return the answer as
IMPOSSIBLE.
If we are able to successfully iterate all the way through $$$\mathbf{S}$$$, then return the A array built while iterating. Since we are iterating through $$$\mathbf{S}$$$ only once and using the hash set, the overall time complexity of this solution is $$$O(\mathbf{N})$$$.
Analysis — D. ASCII Art
Test Set 1
For relatively small values of $$$\mathbf{N}$$$, it suffices to simulate the program in the problem statement to generate characters accordingly and output whichever character gets generated at the $$$\mathbf{N}$$$-th position. Since each character is generated in order and no additional calculation needs to be done, the time complexity of this solution is $$$O(\mathbf{N})$$$, which suffices for Test Set 1.
Test Set 2
The solution described for Test Set 1 would fail for Test Set 2 as $$$\mathbf{N}$$$ is significantly larger here. We would need to utilize the pattern of the characters to improve on it.
One observation we can make is that if we know which iteration of Cody-Jamal's program printed out the $$$\mathbf{N}$$$-th character (let us say it is the $$$i$$$-th iteration) and how many characters were already printed before that (let us say $$$M$$$ characters were already printed before the $$$i$$$-th iteration), we can easily figure out which character is the $$$\mathbf{N}$$$-th character.
Since we know $$$M$$$, we can say that our answer is the $$$(\mathbf{N} - M)$$$-th character printed in
the $$$i$$$-th iteration. Let's define $$$k = \mathbf{N} - M$$$. Clearly, if $$$k \le i$$$,
the character is A, if $$$i \lt k \leq 2i$$$, the character is B
and so on. Simply put, the $$$\mathbf{N}$$$-th character printed is the $$$\lceil \frac{k}{i}
\rceil$$$-th letter of the alphabet, i.e. the $$$\lceil \frac{\mathbf{N} - M}{i} \rceil $$$-th
letter of the alphabet. Also note that if we know $$$i$$$ alone, we can compute $$$M$$$ as
$$$26 \times \sum_{j=1}^{i - 1} j$$$. All that remains is to determine $$$i$$$, which can be done
in the following ways:
Linear Search
We essentially need to find the largest $$$i$$$ such that $$$M = 26 \times \sum_{j=1}^{i - 1} j \lt \mathbf{N}$$$. We can simply compute this sum in order until the point where $$$26 \times \sum_{j=1}^{i - 1} j = 13 \times i \times (i - 1) \geq \mathbf{N}$$$. The time complexity for this approach is $$$O(\sqrt{\mathbf{N}})$$$ since $$$13 \times i \times (i - 1)$$$ increases quadratically.
Binary Search
The previous approach can be sped up by utilizing the fact that $$$13 \times i \times (i - 1)$$$ monotonically increases, which allows us to binary search for $$$i$$$ instead. The bounds for $$$i$$$ to binary search on can be roughly set as 1 and $$$\mathbf{N}$$$. The time complexity in this case is $$$O(\log \mathbf{N})$$$.
Directly Calculating $$$i$$$
As mentioned earlier, we want to find the largest $$$i$$$ such that $$$13 \times i \times (i - 1) \lt \mathbf{N}$$$. Let $$$z$$$ be the positive root of the quadratic equation $$$13 \times i \times (i - 1) - \mathbf{N} = 0$$$. For $$$0 \le i \lt z$$$, the value of $$$13 \times i \times (i - 1) - \mathbf{N}$$$ is negative, after which it becomes positive. Thus, our problem reduces to finding the largest integer $$$i \lt z$$$, which is simply $$$\lceil z - 1 \rceil$$$. $$$z$$$ can be calculated using the quadratic formula as $$$\frac{13 + \sqrt{169 + 52\mathbf{N}}}{26} = \frac{1 + \sqrt{1 + \frac{4\mathbf{N}}{13}}}{2}$$$.
Analysis — E. Untie
Test Set 1
In Test Set 1, the limits are small enough that we can try every possible string made entirely
of Rs, Ps, and Ss as the destination (there are only
$$$3^{10} = 59049$$$ of them). For each one, we can check pairs of adjacent letters to make sure
it is valid. For the valid destinations, we can see how many changes they require, and keep
a running minimum of it.
This solution could be sped up by either generating the strings in a smarter way that does not generate lots of invalid cases only to filter them out later, or by precalculating all valid strings for each length only once, and then using that list directly for each test case. However, none of this is required to pass Test Set 1.
Test Set 2
For Test Set 2 we need a completely different approach, as there are way too many strings to try. We can observe that if we choose any one person, we can always make a choice for them that is different than their neighbors (because there are $$$2$$$ neighbors and $$$3$$$ possible choices). Therefore, any time we have two adjacent equal letters with their other neighbors different, we can always fix it with a single change, and we need at least one. Generalizing that, if we have exactly $$$k$$$ consecutive letters that are equal, surrounded by different ones on both sides, we need at least $$$\lfloor k / 2 \rfloor$$$ changes, and we can do it with exactly that many by changing alternating letters. Therefore, we can add that quantity for each run of consecutive letters (remembering to consider a prefix and a suffix that are made of the same letter as a single run) to the total.
There is one case that we need to solve differently, though. Notice that our precondition above is that a run of consecutive letters is surrounded by other letters. However, if all letters in the input are the same, there is no such run! This case is simple, though, as the answer is, as hinted by Sample Case #2, $$$\lceil$$$the length of $$$\mathbf{C} / 2 \rceil$$$.