Google Kick Start Archive — Round E 2022 problems
Overview
Thank you for participating in Kick Start 2022 Round E!
Cast
Coloring Game: Written by Anurag Singh and prepared by Bryan (Seunghyun) Jo.
Students and Mentors: Written by Carlos Martinez Romero and prepared by Shadman Protik.
Matching palindrome: Written by Bartosz Kostka and prepared by Shadman Protik.
Pizza Delivery: Written by Swante Scholz and prepared by Chun-nien Chan.
Solutions, other problem preparation, reviews and contest monitoring by Abhilash Tayade, Adilet Zhaxybay, Advitiya Brijesh, Alan Lou, Anurag Singh, Bartosz Kostka, Bohdan Pryshchenko, Bryan (Seunghyun) Jo, Carlos Martinez Romero, Chinmay Sagade, Chu-ling Ko, Chun-nien Chan, Cristhian Bonilha, Darpan Shah, Deeksha Kaurav, Diksha Saxena, Duong Hoang, Eunice Hameyie, Hana Joo, Hung-Wei Hung, Jakub Kuczkowiak, Jimmy Dang, Joseph Kottapurath, Kashish Bansal, Krists Boitmanis, Laksh Nachiappan, Lizzie Sapiro Santor, Lucas Maciel, Mantek Singh, Piyush, Pratibha Jagnere, Priyam Khandelwal, Raghul Rajasekar, Rahul Goswami, Rohan Garg, Ruoyu Zhang, Sanyam Garg, Sara Biavaschi, Shadman Protik, Shipra Choudhary, Surya Upadrasta, Swante Scholz, Swapnil Gupta, Swapnil Mahajan, Tanya Chauhan, Teja Vardhan Reddy Dasannagari, Tushar Jape, Umang Goel, Vinay Khilwani, Vishal Som, Yash Ranka.
Analysis authors:
- Coloring Game: Deeksha Kaurav
- Students and Mentors: Adilet Zhaxybay
- Matching palindrome: Krists Boitmanis
- Pizza Delivery: Krists Boitmanis
A. Coloring Game
Problem
John loves to play computer games. He recently discovered an interesting game. In the game there are $$$\mathbf{N}$$$ cells, which are aligned in a row from left to right and are numbered with consecutive integers starting from $$$1$$$. Initially, all cells are coloured white. A cell is valid if it has white color and it does not have any adjacent red colored cell. On each turn, a player paints any valid cell with the red color. The game ends when no valid cells are present. The score of the player is equal to the number of cells they paint.
To master the game, John is practicing against a bot. The bot is poorly trained and it always paints the first valid cell from the left. John on the other hand is playing the game very carefully and he can choose any valid cell. The bot makes the first move and the players take turns alternately.
Find the maximum achievable score by the bot, assuming that John is playing optimally to minimize the score of his opponent.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test
cases follow.
The only line of each test case contains an integer $$$\mathbf{N}$$$ representing the
number of cells in the game.
Output
For each test case, output one line containing
Case #$$$x$$$: $$$y$$$, where $$$x$$$ is the test case number
(starting from 1) and $$$y$$$ is the maximum achievable score by the
bot given that John is playing optimally.
Limits
Time limit: 20 seconds.
Memory limit: 1 GB.
Test Set 1
$$$1 \le \mathbf{T} \le 6$$$.
$$$1 \le \mathbf{N} \le 6$$$.
Test Set 2
$$$1 \le \mathbf{T} \le 100$$$.
$$$1 \le \mathbf{N} \le 10^6$$$.
Sample
3 1 3 6
Case #1: 1 Case #2: 1 Case #3: 2
In Sample Case #1, there is $$$\mathbf{N} = 1$$$ cell. The maximum achievable score by the bot is $$$1$$$.
- First move: The bot paints the first cell with red color.
Since there are no more possible moves, so the game ends. Thus, the answer is $$$1$$$.
In Sample Case #2, there are $$$\mathbf{N} = 3$$$ cells. The maximum achievable score by the bot is $$$1$$$.
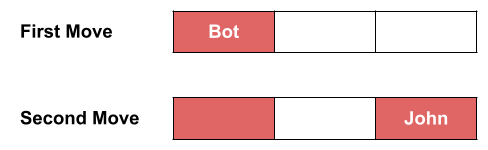
- First move: The bot paints the first cell with red color.
- Second move: John paints the third cell with red color.
Since there are no more possible moves, so the game ends. Thus, the answer is $$$1$$$.
In Sample Case #3, there are $$$\mathbf{N} = 6$$$ cells. The maximum achievable score by the bot is $$$2$$$. In this sample, there exist multiple solutions, one of them would be:
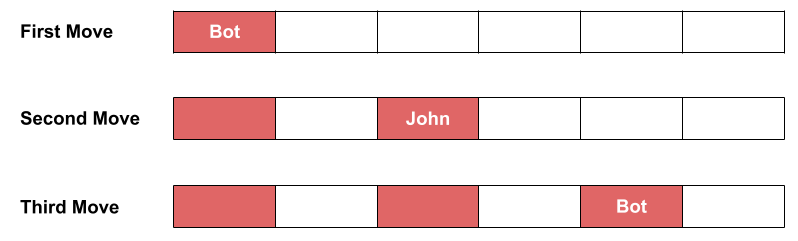
- First move: The bot paints the first cell with red color.
- Second move: John paints the third cell with red color.
- Third move: The bot paints the fifth cell with red color.
Since there are no more possible moves, so the game ends. Thus, the answer is $$$2$$$.
B. Students and Mentors
Problem
A group of $$$\mathbf{N}$$$ students prepares together for upcoming programming competitions such as Kick Start and Code Jam by Google. To help each other prepare, it was decided that each student will pick a mentor among other students. A mentor will help their mentee to solve problems, learn algorithms, track their progress, and will generally support them throughout preparation.
Each student will have exactly one mentor among all other students, and a person can be a mentor to multiple people. For every student $$$i$$$ we know their rating $$$\mathbf{R_i}$$$ which approximates how good that student is at programming competitions. Because it is believed that a mentor should not be much stronger than their mentee, a student $$$j$$$ can be a mentor of student $$$i$$$ only if $$$\mathbf{R_j} \le 2 \times \mathbf{R_i}$$$. Note that a mentor can even have a rating that is lower or equal to their mentee's rating.
Unsurprisingly, each student wants to have the strongest possible mentor. For each student, can you help to figure out what is the highest possible rating of a mentor they can pick?
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow. Each test case consists of two lines.
The first line of each test case contains an integer $$$\mathbf{N}$$$, representing the number of students in a group.
The second line of each test case contains $$$\mathbf{N}$$$ integers $$$\mathbf{R_1} \ \mathbf{R_2} \ \mathbf{R_3} \ \dots \ \mathbf{R_N}$$$ where $$$\mathbf{R_i}$$$ is a rating of the $$$i$$$-th student.
Output
For each test case, output one line containing
Case #$$$x$$$: $$$M_1 \ M_2 \ M_3 \ \dots \ M_N$$$ where $$$x$$$
is the test case number (starting from 1), and $$$M_i$$$ is the maximum
possible rating of the $$$i$$$-th student's mentor or $$$-1$$$ if there
are no suitable mentors for that student.
Limits
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$1 \le \mathbf{R_i} \le 10^6$$$, for all $$$i$$$.
Test Set 1
Time limit: 20 seconds.
$$$2 \le \mathbf{N} \le 1000$$$.
Test Set 2
Time limit: 40 seconds.
$$$2 \le \mathbf{N} \le 10^5$$$.
Sample
3 3 2000 1500 1900 5 1000 600 1000 2300 1800 2 2500 1200
Case #1: 1900 2000 2000 Case #2: 1800 1000 1800 1800 2300 Case #3: 1200 -1
In the Sample Case #1, there are three students with ratings $$$2000$$$, $$$1500$$$, and $$$1900$$$. All students can pick any other student as their mentor, so they all pick a mentor with the highest possible rating. As a result, they pick mentors with ratings $$$1900$$$, $$$2000$$$, and $$$2000$$$, respectively. Note that in this case a student with the rating $$$2000$$$ will be a mentor of two other students.
In the Sample Case #2, there are five students with ratings $$$1000$$$, $$$600$$$, $$$1000$$$, $$$2300$$$, and $$$1800$$$ (note that some students may have equal ratings). For both students with ratings $$$1000$$$, the highest rated possible mentor for them has rating $$$1800$$$. They cannot pick a mentor with rating $$$2300$$$ as $$$2300 > 2 \times 1000$$$. Student with rating $$$600$$$ cannot pick mentors with ratings $$$1800$$$ or $$$2300$$$, so they pick a mentor with rating $$$1000$$$ (either of two students with rating $$$1000$$$ works). Student with rating $$$2300$$$ can pick any other student as their mentor, so they pick a mentor with rating $$$1800$$$ — the highest possible. Finally, student with rating $$$1800$$$ can pick any other student as their mentor too, so they pick a mentor with the highest possible rating of $$$2300$$$. So in the end, the students pick the mentors with the ratings $$$1800$$$, $$$1000$$$, $$$1800$$$, $$$1800$$$, and $$$2300$$$, respectively.
In the Sample Case #3, there are two students with ratings $$$2500$$$ and $$$1200$$$. For a student with rating $$$2500$$$, another student with rating $$$1200$$$ can be a mentor, and there are no other options. For a student with rating $$$1200$$$, we cannot assign a mentor with rating $$$2500$$$, as $$$2500 > 2 \times 1200$$$, and therefore this student has no suitable mentor. In the end, we output $$$1200$$$ and $$$-1$$$ as a result for this test case.
C. Matching Palindrome
Problem
You are given a palindrome string $$$\mathbf{P}$$$ of length $$$\mathbf{N}$$$ consisting of only lowercase letters of the English alphabet. Find the shortest non-empty palindrome string $$$Q$$$ such that $$$\mathbf{P}$$$ concatenated with $$$Q$$$ forms a palindrome. Formally, the string $$$\mathbf{P}Q$$$ forms a palindrome.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow. Each test case consists of two lines. The first line of each test case contains an integer $$$\mathbf{N}$$$ denoting the length of the string $$$\mathbf{P}$$$. The second line of each test case contains a palindrome string $$$\mathbf{P}$$$ of length $$$\mathbf{N}$$$.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$,
where $$$x$$$ is the test case number (starting from 1) and $$$y$$$ is the non-empty palindrome
string $$$Q$$$ as described above.
Limits
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
String $$$\mathbf{P}$$$ is a palindrome consisting of only lowercase letters of the English alphabet.
Test Set 1
Time limit: 20 seconds.
$$$1 \le \mathbf{N} \le 10^3$$$.
Test Set 2
Time limit: 40 seconds.
$$$1 \le \mathbf{N} \le 10^5$$$.
Sample
3 4 abba 4 cccc 6 cdccdc
Case #1: abba Case #2: c Case #3: cdc
In Case 1, the shortest palindrome string $$$Q$$$ is abba such that the concatenation
$$$\mathbf{P}Q$$$ is abbaabba which is a palindrome.
In Case 2, the shortest palindrome string $$$Q$$$ is c such that the concatenation
$$$\mathbf{P}Q$$$ is ccccc which is a palindrome.
In Case 3, the shortest palindrome string $$$Q$$$ is cdc such that the concatenation
$$$\mathbf{P}Q$$$ is cdccdccdc which is a palindrome.
D. Pizza Delivery
Problem
Ada delivers pizzas in a city consisting of a grid of $$$\mathbf{N}$$$ horizontal and $$$\mathbf{N}$$$ vertical streets, heading from North to South and from West to East, respectively, and numbered from $$$1$$$ to $$$\mathbf{N}$$$. The top left street crossing of the grid is $$$(1,1)$$$.
Today, Ada has to deliver $$$\mathbf{P}$$$ pizzas, one for each of $$$\mathbf{P}$$$ customers. Each customer lives at a different street crossing; the $$$k$$$-th customer lives at street crossing $$$(\mathbf{X_k}, \mathbf{Y_k})$$$ and will pay Ada $$$\mathbf{C_k}$$$ coins after the pizza is delivered to their location.
Ada starts at her pizza restaurant at $$$(\mathbf{A_r}, \mathbf{A_c})$$$ with $$$0$$$ coins and carrying $$$\mathbf{P}$$$ pizzas. Her goal is to deliver all of the pizzas within $$$\mathbf{M}$$$ minutes. She is free to take any path she likes around the city and finish deliveries anywhere, as long as she manages to drop off all $$$\mathbf{P}$$$ pizzas to their respective customers within $$$\mathbf{M}$$$ minutes. It takes one minute to walk between two adjacent street crossings, and takes no additional time to drop off a pizza at a customer's location. There are some additional rules and constraints to note:
- Ada is not allowed to go outside the grid.
- No customer lives at the same street crossing as the pizza restaurant Ada starts her trip.
- At any point in time Ada can choose to stay in her current location and not move.
- Ada can also choose not to deliver a pizza when at a customer's location.
Formally, if Ada is currently at street crossing $$$(i,j)$$$, where $$$i$$$ is $$$i$$$-th row from the top, and $$$j$$$ is $$$j$$$-th column from the left, she can decide to do any of the following as long as she does not go outside the grid:
- Go north, she reaches street crossing $$$(i-1, j)$$$.
- Go east, she reaches street crossing $$$(i, j+1)$$$.
- Go west, she reaches street crossing $$$(i, j-1)$$$.
- Go south, she reaches street crossing $$$(i+1, j)$$$.
- Stay at street crossing $$$(i, j)$$$.
The city has a unique toll system in place for using the streets. There is a toll for using each street and the toll depends on Ada's current number of coins and the direction in which she is travelling to. The toll function is defined for every cardinal direction (North, East, West, South) separately. The toll function $$$F_d$$$ for $$$d \in \{ North, East, West, South \}$$$ returns the amount of coins Ada will have after moving in the direction $$$d$$$ and is defined as follows:
$$$F_d$$$ = $$$c$$$ $$$\mathbf{OP_d}$$$ $$$\mathbf{K_d}$$$
where $$$c$$$ is the current number of coins that Ada has and $$$\mathbf{OP_d}$$$ is an operator and $$$\mathbf{K_d}$$$ is a fixed positive integer. The allowed operators are:
+(addition),-(subtraction),*(multiplication),/(integer division).
For example, we can have $$$F_{North}$$$ = $$$c$$$ + $$$3$$$,
$$$F_{East}$$$ = $$$c$$$ * $$$4$$$, $$$F_{West}$$$ = $$$c$$$ - $$$4$$$, $$$F_{South}$$$ = $$$c$$$ / $$$2$$$. That means that if Ada
moves North one street then she will have $$$3$$$ more coins; if Ada
moves East then Ada's coins will quadruple; if Ada moves West then she loses
$$$4$$$ coins; and if Ada moves South then her coins are halved.
All divisions are integer divisions and are computed by using floor function. For example, $$$\frac{-1}{4} = \lfloor\frac{-1}{4}\rfloor = -1$$$. Notice that Ada is allowed to have a negative number of coins. Note that the tolls might actually give Ada coins.
Find out if Ada can deliver all the $$$\mathbf{P}$$$ pizzas in $$$\mathbf{M}$$$ minutes and, if so, the maximum number of coins Ada could have after $$$\mathbf{M}$$$ minutes.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow.
The first line of each test case contains $$$\mathbf{N}$$$, $$$\mathbf{P}$$$, $$$\mathbf{M}$$$, $$$\mathbf{A_r}$$$, $$$\mathbf{A_c}$$$ denoting the grid size, the number of pizzas to deliver, the minutes in which all pizzas should be delivered, and the coordinates of the street crossing at which Ada starts respectively.
The next four lines denote the toll functions for North, East, West, South respectively.
Each of these lines contains $$$\mathbf{OP_d}$$$, denoting the operator (one of +,
-, *, /), and $$$\mathbf{K_d}$$$, the positive integer used in toll
function.
The following $$$\mathbf{P}$$$ lines describe the customers. Each of these lines consists of three integers $$$\mathbf{X_k}$$$, $$$\mathbf{Y_k}$$$, $$$\mathbf{C_k}$$$ denoting the row number of the $$$k$$$-th customer from the top of the grid, the column number of the $$$k$$$-th customer from the left of the grid, and the amount of coins they pay on delivery, respectively.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$,
where $$$x$$$ is the test case number (starting from 1) and $$$y$$$ is IMPOSSIBLE
if all pizzas cannot be delivered within $$$\mathbf{M}$$$ minutes; otherwise, the output should be the
maximum number of coins Ada can have after $$$\mathbf{M}$$$ minutes (which could be negative).
Limits
Time limit: 20 seconds.
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$1 \le \mathbf{N} \le 10$$$.
$$$1 \le \mathbf{M} \le 20$$$.
$$$1 \le \mathbf{A_r}, \mathbf{A_c} \le \mathbf{N}$$$.
$$$1 \le \mathbf{X_k}, \mathbf{Y_k} \le \mathbf{N}$$$, for all $$$k$$$.
$$$1 \le \mathbf{C_k} \le 4$$$, for all $$$k$$$.
$$$1 \le \mathbf{K_d} \le 4$$$, for all $$$d$$$.
$$$\mathbf{OP_d}$$$ is one of (+, -, *, /), for all $$$d$$$.
It is guaranteed that no customer lives at the same street crossing
as the pizza restaurant Ada starts her trip, i.e. $$$(\mathbf{X_k}, \mathbf{Y_k}) \neq (\mathbf{A_r}, \mathbf{A_c})$$$, for all $$$1 \le k \le \mathbf{P}$$$.
It is guaranteed that every customer lives at a different street crossing, i.e. $$$(`X_k, \mathbf{Y_k}) \neq (\mathbf{X_l}, \mathbf{Y_l})$$$, for all $$$1 \le k, l \le \mathbf{P}$$$ and $$$k \neq l$$$.
Test Set 1
$$$\mathbf{P} = 0$$$.
Test Set 2
$$$0 \le \mathbf{P} \le 10$$$.
Sample
Note: there are additional samples that are not run on submissions down below.2 3 0 1 1 2 + 1 - 2 + 3 / 4 3 0 1 2 3 - 2 - 2 - 2 - 2
Case #1: 3 Case #2: 0
In Sample Case #1, Ada does not deliver any pizzas. Ada is located at street crossing
$$$(1,2)$$$. In $$$1$$$ minute she can decide to move west and go to $$$(1,1)$$$, so that the toll at $$$(1,2)$$$
calculates Ada's coins using the toll function F_{West} = $$$c$$$ + $$$3$$$, which results in $$$3$$$
coins. Therefore Ada can have maximum of $$$3$$$ coins with her after $$$1$$$ minute.
In Sample Case #2, Ada does not deliver any pizzas. Ada is located at street crossing
$$$(2, 3)$$$. All directions have a similar toll function, $$$F_d$$$ = $$$c$$$ - $$$2$$$ for all $$$d$$$. If she decides
to go in any direction, she will end up with $$$-2$$$ coins. It is optimal for Ada to stay at the same location
and have $$$0$$$ coins at the end.
Additional Sample - Test Set 2
The following additional sample fits the limits of Test Set 2. It will not be run against your submitted solutions.3 3 1 3 1 3 + 4 - 2 * 1 / 4 1 2 4 2 2 1 1 2 + 2 + 3 * 2 * 1 1 1 4 2 2 1 3 1 2 1 3 + 1 * 1 - 3 / 4 2 2 2
Case #1: 8 Case #2: IMPOSSIBLE Case #3: 1
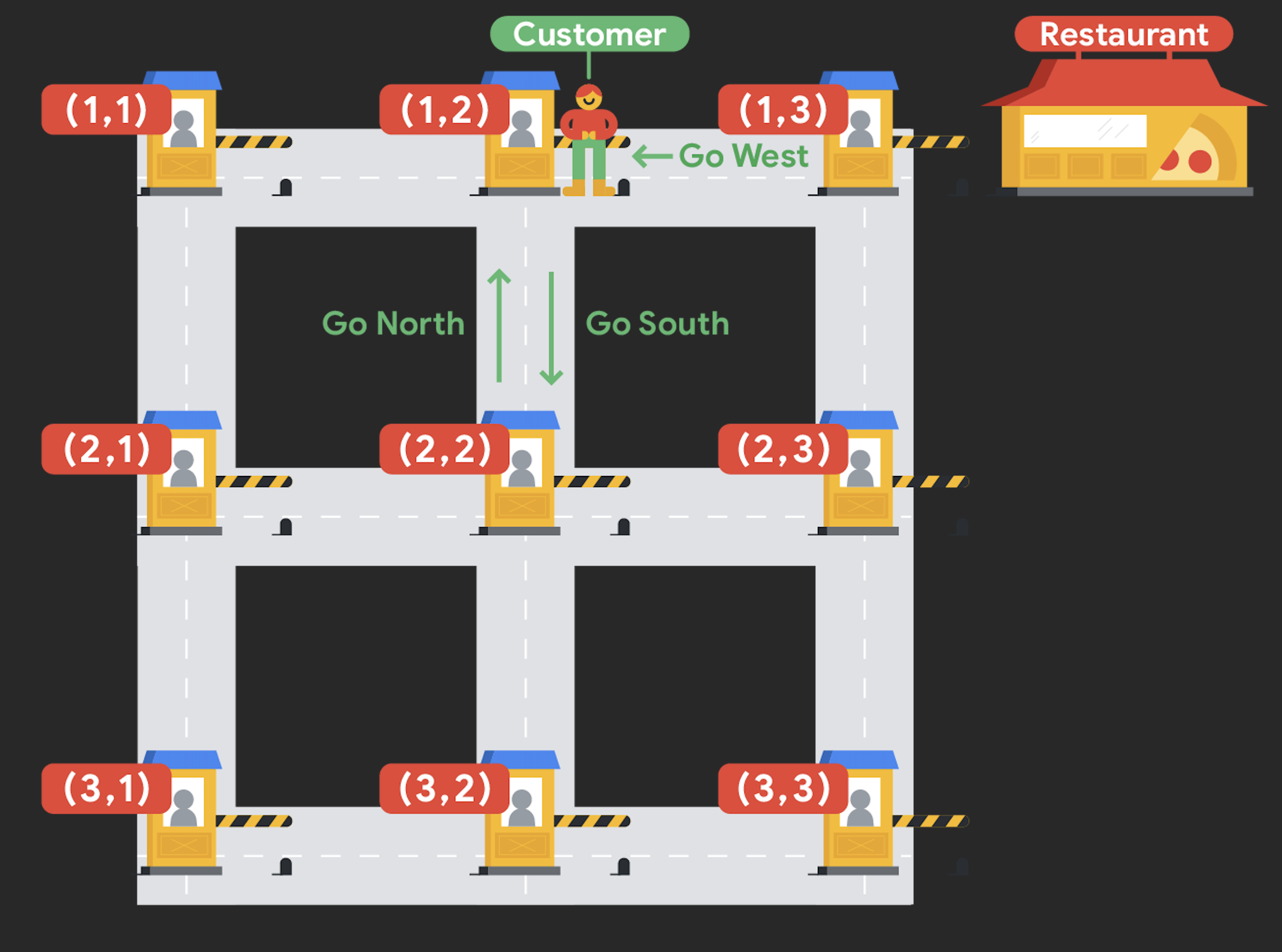
-
Go west to $$$(1,2)$$$. Using the toll function for moving west
$$$F_{west}$$$ = $$$c$$$ * $$$1$$$, Ada now has $$$0 * 1 = 0$$$ coins. -
Do not deliver the pizza at $$$(1,2)$$$ yet, and go south to $$$(2,2)$$$. Using the toll function for moving south
$$$F_{South}$$$ = $$$c$$$ / $$$4$$$, Ada now has $$$0 / 4 = 0$$$ coins. -
Go north to $$$(1,2)$$$. Using the toll function for moving north
$$$F_{North}$$$ = $$$c$$$ + $$$4$$$, Ada now has $$$0 + 4 = 4$$$ coins. - Deliver the pizza at $$$(1,2)$$$. Ada receives $$$4$$$ additional coins for delivering the pizza. Ada has a total of $$$8$$$ coins in the end.
In Additional Sample Case #2, Ada cannot deliver two pizzas in one minute, so the output is
IMPOSSIBLE.
In Additional Sample Case #3, Ada started at street crossing $$$(1,3)$$$ with $$$0$$$ coins. Ada can receive maximum coins by following the steps below:
-
Go west to $$$(1,2)$$$. Using the toll function for moving west
$$$F_{West}$$$ = $$$c$$$ - $$$3$$$, Ada now has $$$0 - 3 = -3$$$ coins. -
Go south to $$$(2,2)$$$. Using the toll function for moving south
$$$F_{South}$$$ = $$$c$$$ / $$$4$$$, Ada now has $$$-3 / 4 = \lfloor\frac{-3}{4}\rfloor = -1$$$ coins. - Deliver the pizza at $$$(2,2)$$$. Ada receives $$$2$$$ additional coins for delivering the pizza. Ada has a total of $$$1$$$ coins in the end.
Analysis — A. Coloring Game
Let us use the following notation for the analysis:
- Cells painted by the bot are marked as $$$B$$$.
- Cells painted by John are marked as $$$J$$$.
- Valid cells are marked as $$$V$$$.
- Invalid cells are marked as $$$X$$$.
Let us first look at the case with $$$\mathbf{N}=5$$$. All cells are valid in the beginning.
Initial state: $$$[V, V, V, V, V]$$$.
The cell numbered with integer $$$i$$$ is represented as $$$C_i$$$. As the bot makes the first move, it colors the leftmost valid cell, which is $$$C_1$$$. This move makes the cells $$$C_1$$$ and $$$C_2$$$ invalid and reduces the number of valid cells by $$$2$$$.
State after first move: $$$[B, X, V, V, V]$$$.
As John plays optimally to minimize the bot's score, he colors a cell which makes as many invalid cells as possible. Coloring the cell $$$C_3$$$, which is adjacent to an invalid cell, makes the cells $$$C_3$$$ and $$$C_4$$$ invalid, while coloring the cell $$$C_4$$$ makes the cells $$$C_3$$$, $$$C_4$$$ and $$$C_5$$$ invalid. Thus, John colors the cell $$$C_4$$$, reducing the number of valid cells by $$$3$$$ and leaving no more cells for the bot to color in the next turn.
State after John's move: $$$[B, X, X, J, X]$$$
Test Set 1
For $$$\mathbf{N} \le 5$$$, the bot can color at most 1 cell in its first move and John can make the remaining cells invalid. Thus, maximum achievable score by the bot for $$$\mathbf{N} \le 5$$$ is $$$1$$$.
For $$$\mathbf{N} = 6$$$, the bot can color another cell in the second move. Thus, maximum achievable score by the bot for $$$\mathbf{N} = 6$$$ is $$$2$$$.
Test Set 2
Since the bot always paints the first valid cell from the left, we can show that after each move by the bot, the number of valid cells reduces by at most $$$2$$$. Also, after each move by John, the number of valid cells reduces by at most $$$3$$$. We can show that this is achievable if John always paints the second valid cell from the left unless there is only one valid cell remaining. This results in reduction of the number of valid cells by at most $$$5$$$ between successive turns of the bot.
In other words, the bot paints $$$1$$$ cell for every $$$5$$$ cells. Thus, the total number of cells the bot can paint is at least $$$\lceil\mathbf{N}/5\rceil$$$.
Time and Space Complexity: The answer for both the test sets can be found in $$$O(1)$$$ time and no extra space is required for calculating the answer.
Analysis — B. Students and Mentors
Test Set 1
In Test Set 1, you can simply try all possible options. For each student, check all the other students as a potential mentor, and choose the highest rated possible one. The time complexity of this solution will be $$$O(N^2)$$$, which is enough for this test set.
Test Set 2
In Test Set 2, we have $$$\mathbf{N} \le 10^5$$$, and $$$O(N^2)$$$ will take too much time, so a smarter, more efficient solution is needed. Below are two of the possible approaches.
Binary Search
If we sort an array of student ratings, then for each $$$R_i$$$ we can find the maximum $$$R_j $$$ such that $$$R_j \le 2 \times R_i$$$ using binary search. The only caveat is that an extra care is required to prevent picking yourself as the highest rated possible mentor. We can prevent this from happening as follows. Make sure the binary search chooses the rightmost one of the several equal ratings in an array. Then if the rating of the mentor for a student $$$i$$$ found with binary search is equal to $$$R_i$$$, we take rating to the left of it as an answer, or output $$$-1$$$ if it is the first element of an array.
The time complexity of this solution will be $$$O(\mathbf{N}\log \mathbf{N})$$$ because of sorting and performing binary search $$$\mathbf{N}$$$ times.
Two Pointers
If we have a sorted array of student ratings, we could also use the two pointer approach to solve the problem. Let us consider students one by one, from the lowest rated ones to the highest rated ones, and try to find the ratings of the mentors for them. As we do this, we will maintain a "pointer" to the index of the highest possible rating of a mentor for the current student. Initially the pointer will be at the start of the array. Notice that as your consider the student with the higher rating and try to find the mentor for them, pointer to the highest possible mentor rating can move only to the right in the sorted array of ratings. As such, we can simply try to move the pointer to the right as far as we can for each student, and it will move no more than $$$\mathbf{N}$$$ times in total. An additional care is required to prevent picking yourself as a mentor, similarly to the binary search solution.
The time complexity of this solution will also be $$$O(\mathbf{N}\log \mathbf{N})$$$ because you need to sort the array first. As a fun variation, it is also possible to trade time for space, and use the fact that $$$\max(R_i) \le 10^6$$$. We can then sort the array of ratings using an array of size $$$10^6$$$ and a variation of counting sort, and later execute two pointer part of the solution in $$$O(N)$$$. Total time complexity of the solution will be $$$O(\max(N, \max(R_i)))$$$, or $$$O(N)$$$ as $$$\max(R_i) \approx 10 \times N$$$, although in practice it might be not much faster than $$$O(\mathbf{N}\log \mathbf{N})$$$ solution.
Analysis — C. Matching Palindrome
We should not consider any string $$$Q$$$ longer than $$$\mathbf{P}$$$ itself because $$$\mathbf{P}\mathbf{P}$$$ is a palindrome and we can always use $$$Q=\mathbf{P}$$$ if there is no shorter valid string $$$Q$$$. Hence, in what follows, we assume that $$$|Q| \le |\mathbf{P}|$$$.
Since $$$\mathbf{P}Q$$$ is a palindrome, $$$\mathbf{P}$$$ must start with the reverse of $$$Q$$$, which is $$$Q$$$ itself since $$$Q$$$ is a palindrome. Thus $$$\mathbf{P}=QX$$$ for some suffix $$$X$$$.
Test Set 1
We can check every prefix $$$Q$$$ of $$$\mathbf{P}$$$ and verify if $$$Q$$$ and $$$\mathbf{P}Q$$$ are both palindromes. The shortest of such valid prefixes $$$Q$$$ is our answer. Any given prefix $$$Q$$$ can be verified in linear time, and the overall time complexity of this brute-force algorithm is therefore $$$O(\mathbf{N}^2)$$$.
Test Set 2
The time complexity of the naive algorithm above can be improved to $$$O(\mathbf{N})$$$ using string hashing, which is a widely applicable technique for various string matching problems. In this section, though, we discuss two other approaches.
Manacher's Algorithm
So we are looking for the shortest palindromic prefix $$$Q$$$ such that $$$\mathbf{P}=QX$$$ and $$$QXQ$$$ is also a palindrome. It follows that the suffix $$$X$$$ must be palindromic as well. Our task is then to split the string $$$\mathbf{P}$$$ into two palindromes $$$Q$$$ and $$$X$$$ such that $$$Q$$$ is as short as possible. Finding such a split would be a trivial task if we knew in advance if any particular prefix or suffix of $$$\mathbf{P}$$$ is a palindrome.
This is where the linear time Manacher's algorithm can help. Its main purpose is to find the longest palindromic substring in a given string, however, the algorithm does more than that. Assuming $$$\mathbf{P}=p_1p_2p_3 \ldots p_\mathbf{N}$$$, Manacher's algorithm finds the longest palindromic substring of odd length centered at any particular letter $$$p_i$$$ and similarly the longest palindromic substring of even length centered at any particular pair of letters $$$p_ip_{i+1}$$$. Now, how do we know if a certain prefix $$$\mathbf{P}=p_1p_2p_3 \ldots p_k$$$ of, say, odd length is a palindrome? It is a palindrome precisely when the length of the longest palindromic substring centered at $$$p_\frac{k+1}{2}$$$ is $$$k$$$. In a similar vein, we can test if a prefix of even length or any suffix is palindromic.
The overall time complexity of this solution is $$$O(\mathbf{N})$$$.
Optimized Brute-Force Algorithm
There is a much simpler algorithm if you trust your intuition that for the shortest prefix $$$Q$$$, the string $$$\mathbf{P}$$$ must be of the form $$$\mathbf{P}=Q^k$$$ for some $$$k \ge 1$$$. If this assumption holds true, then we can use a modification of the same brute-force algorithm above, where we test a prefix $$$Q$$$ only if $$$|Q|$$$ divides $$$\mathbf{N}$$$. There are only $$$128$$$ divisors of $$$\mathbf{N}$$$ in the worst case given the constraints of the problem, and that is a small enough constant.
The time complexity of this modified algorithm is $$$O(\mathbf{N}\sqrt{\mathbf{N}})$$$ or better depending on the function we use for approximating the number of divisors of $$$\mathbf{N}$$$.
It remains to show that our assumption indeed holds.
Claim: If $$$X$$$, $$$Y$$$, and $$$S=XY$$$ are all palindromic strings, then $$$X=Z^k$$$ and $$$Y=Z^l$$$ for some palindrome $$$Z$$$ and some integers $$$k \ge 1$$$ and $$$l \ge 1$$$.
Proof: We will prove the claim using mathematical induction on $$$|S|$$$. Without loss of generality, let us assume that $$$|X| \le |Y|$$$. Since $$$S$$$ is a palindrome with the prefix $$$X$$$, $$$S$$$ must also end in $$$X$$$ (and so must $$$Y$$$). Now, since $$$Y$$$ is a palindrome with the suffix $$$X$$$, $$$Y$$$ must also start with $$$X$$$, and consequently $$$S$$$ has a prefix $$$XX$$$. And again, since $$$S$$$ is a palindrome, $$$XX$$$ must be a suffix of both $$$S$$$ and $$$Y$$$. And continuing this back and forth process, we may conclude that $$$S=X^tWX^t$$$, where $$$W$$$ is a palindromic substring in the middle of $$$S$$$ and $$$|W| \lt 2|X|$$$. We consider four possible cases:
- $$$|W|=\emptyset$$$: This is a base case of our inductive proof. The entire string $$$S$$$ is a power of $$$X$$$, hence we can choose $$$Z=X$$$.
- $$$|W|=|X|$$$: Another base case. Since the palindrome $$$Y$$$ equals $$$X^{t-1}WX^t$$$, $$$W$$$ must be $$$X$$$, and again, $$$S$$$ is a power of $$$X$$$.
- $$$0 \lt |W| \lt |X|$$$: Since $$$Y=X^{t-1}WX^t$$$ is a palindrome, the substring $$$WX$$$ in the middle must be palindromic as well. Recall that both $$$W$$$ and $$$X$$$ are palindromes and $$$|WX| \lt |S|$$$, hence, by inductive hypothesis, $$$W$$$ and $$$X$$$ must be powers of some palindrome $$$Z$$$, and so is $$$S$$$.
- $$$|X| \lt |W| \lt 2|X|$$$: Again, $$$Y=X^{t-1}WX^t$$$ is a palindrome, so $$$W$$$ must be of the form $$$XR$$$, where $$$R$$$ is palindromic. Since $$$|W| \lt |S|$$$, the palindromes $$$X$$$ and $$$R$$$ are powers of some palindrome $$$Z$$$ by inductive hypothesis.
That concludes the proof of our claim.
To connect the dots, let us see how this claim validates our optimization of the brute-force algorithm. Suppose we split $$$\mathbf{P}$$$ into two palindromes $$$Q$$$ and $$$Y$$$ and $$$|Q|$$$ does not divide $$$\mathbf{N}$$$. Then, by the claim, both $$$Q$$$ and $$$Y$$$ are powers of a shorter palindrome $$$Z$$$, and $$$Q$$$ can be disregarded in favour of $$$Z$$$.
Analysis — D. Pizza Delivery
Test Set 1
Since Ada does not have to deliver any pizzas in this test set, our task is simply to find the most profitable path of $$$\mathbf{M}$$$ steps starting from the location $$$(\mathbf{A_r},\mathbf{A_c})$$$. It is important to note that the functions $$$F_i(c)$$$ are increasing given that $$$\mathbf{K_i} \ge 1$$$. In other words, to maximize the outcome of the functions, we should try maximizing the current number of coins $$$c$$$. Therefore, to find the profit of an optimal path of length $$$\mathbf{M}$$$ from $$$(\mathbf{A_r},\mathbf{A_c})$$$ to a specific location $$$(i,j)$$$, we must find optimal paths of length $$$\mathbf{M}-1$$$ to all of its neighbouring locations first, apply the respective toll functions $$$F$$$, and take the maximum outcome. And whenever we can reduce a problem to the same but smaller sub-problems, dynamic programming can help most of the time.
Formally, let $$$DP_{i,j,t}$$$ be the maximum profit of a path of length $$$t$$$ from $$$(\mathbf{A_r},\mathbf{A_c})$$$ to the location $$$(i,j)$$$ and let $$$L_{i,j}$$$ be the neighbouring locations of $$$(i,j)$$$ ($$$|L_{i,j}| \le 4$$$). Then
$$$DP_{i,j,0}=\left\{ \begin{matrix} 0 & \textrm{if } (i,j)=(\mathbf{A_r},\mathbf{A_c}) \\ -\infty & \textrm{otherwise} \end{matrix}\right.$$$
and
$$$DP_{i,j,t+1}=\max(DP_{i,j,t}, \max_{(i',j') \in L_{i,j}} DP_{i',j',t} \mathbf{OP_*} \mathbf{K_*})$$$.
For brevity, $$$\mathbf{OP_*} \mathbf{K_*}$$$ refers to the appropriate function $$$F$$$ when going from location $$$(i',j')$$$ to location $$$(i,j)$$$. Note that Ada can choose to not move at all, hence the term $$$DP_{i,j,t}$$$ in the recurrence above.
The final answer is $$$\max_{1 \le i,j \le \mathbf{N}} DP_{i,j,\mathbf{M}}$$$. The time complexity for computing the entire $$$DP$$$ table is $$$O(\mathbf{N}^2\mathbf{M})$$$.
Test Set 2
In the case Ada actually has to deliver some pizzas, the problem can be solved in much the same way, except that we need to keep track of the pizzas that have been delivered already. So instead of asking, what is the best way to reach the location $$$(i,j)$$$ in $$$t$$$ steps, we are wondering, what is the best way to deliver a subset $$$S \subseteq \{1,2,\ldots,\mathbf{P}\}$$$ of pizzas in $$$t$$$ steps and end up in the location $$$(i,j)$$$. All we have to do is extend our $$$DP$$$ table by another dimension, namely, all the possible subsets $$$S$$$ of pizzas.
Formally, let $$$DP_{i,j,S,t}$$$ be the maximum profit of delivering the subset of pizzas $$$S$$$ in $$$t$$$ steps and ending up at the location $$$(i,j)$$$. Then
$$$DP_{i,j,S,0}=\left\{ \begin{matrix} 0 & \textrm{if } (i,j)=(\mathbf{A_r},\mathbf{A_c}) \textrm{ and } S=\emptyset \\ -\infty & \textrm{otherwise} \end{matrix}\right.$$$.
As for the recurrence relation, we must account for Ada's choice to deliver pizzas after each step. If none of the customers in $$$S$$$ lives at the location $$$(i,j)$$$, then delivering a pizza after the next step is not an option, and our recurrence relation remains the same:
$$$DP_{i,j,S,t+1}=\max(DP_{i,j,S,t}, \max_{(i',j') \in L_{i,j}} DP_{i',j',S,t} \mathbf{OP_*} \mathbf{K_*})$$$.
However, if, say, customer $$$x$$$ lives at the location $$$(i,j)$$$ and $$$x \in S$$$, then Ada can choose to deliver their pizza after making the next step, therefore, our recurrence relation becomes
$$$DP_{i,j,S,t+1}=\max(DP_{i,j,S,t}, DP_{i,j,S-\{x\},t}+\mathbf{C_x}, \max_{(i',j') \in L_{i,j}} DP_{i',j',S,t} \mathbf{OP_*} \mathbf{K_*}, \max_{(i',j') \in L_{i,j}} DP_{i',j',S-\{x\},t} \mathbf{OP_*} \mathbf{K_*} + \mathbf{C_x})$$$.
The final answer is $$$\max_{1 \le i,j \le \mathbf{N}} DP_{i,j,\{1,2,\ldots,\mathbf{P}\}, \mathbf{M}}$$$ and the time complexity of the algorithm is now $$$O(\mathbf{N}^2 2^\mathbf{P} \mathbf{M})$$$.