Google Kick Start Archive — Round D 2022 problems
Overview
Thank you for participating in Kick Start 2022 Round D!
Cast
Image Labeler: Written by Venkat and prepared by Bryan (Seunghyun) Jo.
Maximum Gain: Written by Anuj Singh and prepared by Bryan (Seunghyun) Jo.
Touchbar Typing: Written by Jiahui Feng and prepared by Jared Gillespie.
Suspects and Witnesses: Written by Kai Hsien Boo and prepared by Adilet Zhaxybay.
Solutions, other problem preparation, reviews and contest monitoring by Abhilash Tayade, Adilet Zhaxybay, Advitiya Brijesh, Alejandro Rivera, Anuj Singh, Bartosz Kostka, Bohdan Pryshchenko, Brijesh Panara, Bryan (Seunghyun) Jo, Chinmaya Kar, Chu-ling Ko, Chun-nien Chan, Cristhian Bonilha, Daksh Varshney, Duong Hoang, Ekanshi Agrawal, Jared Gillespie, Jiahui Feng, Jimmy Dang, Kai Hsien Boo, Kunal Verma, Kushagra Srivastava, Laksh Nachiappan, Liam Healy, Lucas Maciel, Luis Santiago Re, Madhurima Maji, Matt Kenison, Nga Tran, Nomaan Shaikh, Piyush, Pratibha Jagnere, Priyam Khandelwal, Rahul Goswami, Rakesh Theegala, Rayan Dasoriya, Ruiqing Xiang, Sachin Yadav, Sadia Atique, Samah Abu Shamma, Sanyam Garg, Saptarshi Mukherjee, Satish Karri, Shipra Choudhary, Shivam Dubey, Surya Upadrasta, Suryansh Gupta, Swapnil Gupta, Tarun Khullar, Teja Vardhan Reddy Dasannagari, Tushar Jape, Uday Patel, Umang Goel, Venkat, Vijay Krishan Pandey, Vinay Khilwani, Vishal Som, Yash Ranka, Zongxin Wu.
Analysis authors:
- Image Labeler: Matt Kenison
- Maximum Gain: Chun-nien Chan
- Touchbar Typing: Sadia Atique
- Suspects and Witnesses: Uday Patel
A. Image Labeler
Problem
Crowdsource is organizing a campaign for Image Labeler task with participants across $$$\mathbf{N}$$$ regions. The number of participants from each of these regions are represented by $$$\mathbf{A_1}, \mathbf{A_2}, \dots, \mathbf{A_N}$$$.
In the Image Labeler task, there are $$$\mathbf{M}$$$ categories. Crowdsource assigns participants to these categories in such a way that all participants from a region are assigned to the same category, and each category has at least one region assigned to it. The success metric of the campaign is measured by the sum of medians of the number of participants in each category. (Let us remind you here that the median of a list of integers is the "middle" number when those numbers are sorted from smallest to largest. When the number of integers in a list is even, we have two "middle" numbers, therefore the median is defined as the arithmetic mean (average) of the two middle values.)
For example, imagine that we have $$$\mathbf{N}=3$$$ regions with $$$\mathbf{A_1}=5$$$, $$$\mathbf{A_2}=8$$$, and $$$\mathbf{A_3}=9$$$ participants respectively and we want to assign them to $$$\mathbf{M}=2$$$ categories. If we assign regions $$$2$$$ and $$$3$$$ to category $$$1$$$ and region $$$1$$$ to category $$$2$$$, then the success metric would be median of $$$\{A_2=8, A_3=9\}\ + $$$ median of $$$\{A_1=5\} = \frac{8 + 9}{2} + 5 = 8.5 + 5 = 13.5$$$. We can also assign regions $$$1$$$ and $$$2$$$ to category $$$1$$$ and region $$$3$$$ to category $$$2$$$. Then the success metric would be equal to the sum of the median of $$$\{A_1=5, A_2=8\}$$$ and the median of $$$\{A_3=9\}$$$, which is $$$\frac{5+8}{2} + 9 = 6.5 + 9 = 15.5$$$.
Your task is to find the maximum possible value of the success metric that can be obtained by assigning participants in regions to the categories.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test
cases follow.
The first line of each test case contains two integers $$$\mathbf{N}$$$ and $$$\mathbf{M}$$$: the number
of regions, and the number of categories respectively.
The next line contains $$$\mathbf{N}$$$ integers $$$\mathbf{A_1}, \mathbf{A_2}, \dots, \mathbf{A_N}$$$.
Output
For each test case, output one line containing
Case #$$$x$$$: $$$y$$$, where $$$x$$$ is the test case number
(starting from 1) and $$$y$$$ is the maximum possible value of the success
metric.
$$$y$$$ will be considered correct if it is within an
absolute or relative error of $$$10^{-6}$$$ of the correct answer. See the
FAQ
for an explanation of what that means, and what formats of real numbers
we accept.
Limits
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$1 \le \mathbf{N} \le 10^4$$$.
$$$1 \le \mathbf{M} \le 10^4$$$.
$$$1 \le \mathbf{M} \le \mathbf{N}$$$.
$$$1 \le \mathbf{A_i} \le 10^5$$$, for all $$$i$$$.
Test Set 1
Time limit: 20 seconds.
$$$0 \le \mathbf{N} - \mathbf{M} \le 1$$$.
Test Set 2
Time limit: 40 seconds.
No additional constraints.
Sample
Note: there are additional samples that are not run on submissions down below.1 3 2 11 24 10
Case #1: 34.5
- Assign $$$\{11, 24\}$$$ to category $$$1$$$ and $$$\{10\}$$$ to category $$$2$$$, in which case the success metric is $$$\frac{11 + 24}{2} + 10 = 17.5 + 10 = 27.5$$$.
- Assign $$$\{24, 10\}$$$ to category $$$1$$$ and $$$\{11\}$$$ to category $$$2$$$, in which case the success metric is $$$\frac{24 + 10}{2} + 11 = 17 + 11 = 28$$$.
- Assign $$$\{11, 10\}$$$ to category $$$1$$$ and $$$\{24\}$$$ to category $$$2$$$, in which case the success metric is $$$\frac{11 + 10}{2} + 24 = 10.5 + 24 = 34.5$$$.
- $$$3$$$ other ways, where assignments to category $$$1$$$ and $$$2$$$ are swapped, which does not alter the value of success metric.
Additional Sample - Test Set 2
The following additional sample fits the limits of Test Set 2. It will not be run against your submitted solutions.1 5 1 6 2 5 1 9
Case #1: 5.0
In this test, there is only one category, so participants in all regions will be assigned to it. The only possible value of the success metric is the median of $$$\{6, 2, 5, 1, 9\}$$$ which is $$$5$$$.
B. Maximum Gain
Problem
Charles is participating in an event of Crowdsource tasks and he is most enthusiastic to gain the maximum points from there! There are two Crowdsource tasks: Audio Validation Task and Image Labeler Task. Each task consists of a list of questions. Charles is given two arrays ($$$\mathbf{A}$$$ and $$$\mathbf{B}$$$) representing the two tasks. Each element of an array indicates the number of points that Charles will gain by answering the corresponding question.
Charles is allowed to answer $$$\mathbf{K}$$$ questions in total, from both tasks, one at a time. At each step, he is allowed to choose a task (that is, choose one of the two arrays) that has remaining unanswered questions. He is then allowed to answer either the first or the last question, from the list of remaining questions of this task. Once he answers the question, he gets the corresponding points and the answered question is removed from the task.
Can you help Charles choose the questions that will give him the maximum possible points?
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test
cases follow.
The first line of each test case contains an integer $$$\mathbf{N}$$$, which denotes the number of elements in
the first array.
The second line of each test case contains $$$\mathbf{N}$$$ integers $$$\mathbf{A_1}, \mathbf{A_2}, \dots, \mathbf{A_N}$$$.
$$$\mathbf{A_i}$$$ denotes the points gained for answering the $$$i$$$-th question of Audio
Validation Task.
The third line of each test case contains an integer $$$\mathbf{M}$$$, which denotes the number of elements in
the second array.
The fourth line of each test case contains $$$\mathbf{M}$$$ integers $$$\mathbf{B_1}, \mathbf{B_2}, \dots, \mathbf{B_M}$$$.
$$$\mathbf{B_i}$$$ denotes the points gained for answering the $$$i$$$-th question of Image
Labeler Task.
The fifth line of each test case contains an integer $$$\mathbf{K}$$$, which denotes the number of elements to
be selected in total, from both arrays, using the process described above.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$, where $$$x$$$
is the test case number (starting from 1) and $$$y$$$ is the maximum number of points that
Charles can gain in this test case.
Limits
Time limit: 30 seconds.
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$1 \le \mathbf{N} \le 6000$$$.
$$$1 \le \mathbf{M} \le 6000$$$.
$$$1 \le \mathbf{A_i}, \mathbf{B_i} \le 10^9$$$, for all $$$i$$$.
$$$1 \le \mathbf{K} \le \mathbf{N}+\mathbf{M}$$$.
Test Set 1
$$$1 \le \mathbf{K} \le 30$$$.
Test Set 2
$$$1 \le \mathbf{K} \le 3000$$$.
Sample
2 3 3 1 2 4 2 8 1 9 5 4 1 100 4 3 6 15 10 12 5 1 10 6
Case #1: 24 Case #2: 148
In Sample Case #1, Charles can answer $$$5$$$ questions. If he chooses the first and last questions from the first array, he gets $$$(3+2)$$$ points. If he chooses the first two questions and the last question from the second array, he gets $$$(2+8+9)$$$ points. Thus, by answering these $$$5$$$ questions, Charles gets $$$((3+2)+(2+8+9)) = 24$$$ points. This happens to be the maximum possible number of points that Charles can obtain in this test case. A non-optimal selection could be to choose the last two elements from the first array, the first element from the second array, and last two elements from the second array. This would have yielded $$$((1+2)+(2+1+9)) = 15$$$ points.
In Sample Case #2, Charles can answer $$$6$$$ questions. If he chooses the first two from the first array, he gets $$$(1+100)$$$ points. If he chooses the first three questions and the last question from the second array, he gets $$$(15+10+12+10)$$$ points. Thus, selecting these $$$6$$$ questions, Charles gets $$$((1+100)+(15+10+12+10)) = 148$$$ points, which happens to be the maximum value for this case.
C. Touchbar Typing
Problem
Glide Typing task in Crowdsource app uses a new Google keyboard to type a word by sliding a finger across keys without lifting the finger, as shown in the animation below.
To make the Glide Typing task more challenging, instead of a normal keyboard, we have a special linear keyboard $$$\mathbf{K}$$$ that has all the keys in one row.
Imagine that you want to type a word $$$\mathbf{S}$$$ that is $$$\mathbf{N}$$$ characters long. The linear keyboard $$$\mathbf{K}$$$ has $$$\mathbf{M}$$$ keys. It is guaranteed that the keys cover all characters in $$$\mathbf{S}$$$. However, some of the keys may be duplicates. In other words, for each character in $$$\mathbf{S}$$$, there is one or more keys in $$$\mathbf{K}$$$ mapped to the character. Note that, all characters and keys are represented as integers.
You may start with your finger on any key. It takes $$$1$$$ second to move your finger from a key to an adjacent key. Due to Glide Typing, there is no pressing a key. If the finger is currently at the key $$$i$$$ which has character $$$\mathbf{K_i}$$$, and we want to type the character $$$\mathbf{K_j}$$$ at index $$$j$$$, we will glide the finger from the key $$$i$$$ to the key $$$j$$$, which takes $$$\lvert j-i \rvert$$$ seconds. If your finger is at key $$$x$$$, you can type character $$$\mathbf{K_x}$$$ any number of times instantly. You need to type string $$$\mathbf{S}$$$ character by character. Formally, you need to type $$$\mathbf{S_i}$$$ before $$$\mathbf{S_{i+1}}$$$ for each $$$ 1 \le i \le \mathbf{N}-1 $$$.
For example, suppose the word $$$\mathbf{S}$$$ has characters: 1, 2, 2,
3, 4. You can start by keeping your finger
on key with character 1 on the keyboard which is at index $$$i$$$. Then you glide
your finger to key which has character 2
which is at index $$$j$$$. It would take $$$\lvert j-i \rvert$$$ seconds. In order
to type character 2 two times in string $$$\mathbf{S}$$$, you can do that in no additional time
as $$$\lvert j-j \rvert = 0$$$ seconds. Then you can continue to glide your finger to type the other characters
in the word $$$\mathbf{S}$$$ sequentially.
Can you calculate the minimal time needed to type the word?
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow.
The first line of each test case contains one integer $$$\mathbf{N}$$$: the length of the
word $$$\mathbf{S}$$$.
The second line of each test case contains $$$\mathbf{N}$$$ integers: each $$$\mathbf{S_i}$$$ is the
character at the $$$i$$$-th index.
The third line of each test case contains one integer $$$\mathbf{M}$$$: the length of the
keyboard $$$\mathbf{K}$$$.
The fourth line of each test case contains $$$\mathbf{M}$$$ integers: each $$$\mathbf{K_i}$$$ is the
character at the $$$i$$$-th key.
Output
For each test case, output one line containing the minimal time needed to type the
word.
Case #$$$x$$$: $$$y$$$, where $$$x$$$ is the test case number
(starting from 1) and $$$y$$$ is the minimal time needed to type $$$\mathbf{S}$$$ on the keyboard
$$$\mathbf{K}$$$.
Limits
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
All characters in $$$\mathbf{S}$$$ appears at least once in $$$\mathbf{K}$$$.
$$$1 \le \mathbf{K_i} \le 2500$$$.
$$$1 \le \mathbf{S_i} \le 2500$$$.
Test Set 1
Time limit: 20 seconds.
$$$1 \le \mathbf{N} \le 100$$$.
$$$1 \le \mathbf{M} \le 100$$$.
It is guaranteed that there are no duplicated keys in keyboard $$$\mathbf{K}$$$.
Test Set 2
Time limit: 20 seconds.
$$$1 \le \mathbf{N} \le 100$$$.
$$$1 \le \mathbf{M} \le 100$$$.
Test Set 3
Time limit: 40 seconds.
$$$1 \le \mathbf{N} \le 2500$$$.
$$$1 \le \mathbf{M} \le 2500$$$.
Sample
Note: there are additional samples that are not run on submissions down below.2 5 1 2 3 2 1 3 1 2 3 3 1 1 1 2 2 1
Case #1: 4 Case #2: 0
In Sample Case #1, we can take the following steps to type string $$$\mathbf{S}$$$ in minimum time.
-
Start by keeping your finger on key $$$\mathbf{K_1}$$$ which has character
1. We have now typed the first character of the string $$$\mathbf{S}$$$. -
In order to type the second character
2of the string $$$\mathbf{S}$$$, glide your finger to key $$$\mathbf{K_2}$$$. it takes $$$\lvert 2 - 1 \rvert = 1$$$ additional second to glide the finger from index $$$1$$$ to index $$$2$$$. -
In order to type the third character
3of the string $$$\mathbf{S}$$$, glide your finger to key $$$\mathbf{K_3}$$$. it takes $$$\lvert 3 - 2 \rvert = 1$$$ additional second to glide the finger from index $$$2$$$ to index $$$3$$$. -
In order to type the fourth character
2of the string $$$\mathbf{S}$$$, glide your finger to key $$$\mathbf{K_2}$$$. it takes $$$\lvert 2 - 3 \rvert = 1$$$ additional second to glide the finger from index $$$3$$$ to index $$$2$$$. -
In order to type the fifth character
1of the string $$$\mathbf{S}$$$, glide your finger to key $$$\mathbf{K_1}$$$. it takes $$$\lvert 1 - 2 \rvert = 1$$$ additional second to glide the finger from index $$$2$$$ to index $$$1$$$. - We have typed all characters of the string $$$\mathbf{S}$$$ in a total of $$$4$$$ seconds.
In Sample Case #2, we can take the following steps to type string $$$\mathbf{S}$$$ in minimum time.
-
Start by keeping your finger on key $$$\mathbf{K_2}$$$ which has character
1. We have now typed the first character of the string $$$\mathbf{S}$$$. -
As our finger is on key $$$\mathbf{K_2}$$$, we can type the character
1any number of times, without any additional time. Hence, we can type the second and third characters of the string $$$\mathbf{S}$$$. - We have typed all characters of the string $$$\mathbf{S}$$$ in a total of $$$0$$$ seconds.
Additional Sample - Test Set 2
The following additional sample fits the limits of Test Set 2. It will not be run against your submitted solutions.2 4 2 1 4 1 8 4 1 5 2 1 3 5 4 3 1 2 3 8 2 3 5 1 4 6 7 2
Case #1: 4 Case #2: 4
In Additional Sample Case #1, we can take the following steps to type string $$$\mathbf{S}$$$ in minimum time.
-
Start by keeping your finger on key $$$\mathbf{K_4}$$$ which has character
2. We have now typed the first character of the string $$$\mathbf{S}$$$. -
In order to type the second character
1of the string $$$\mathbf{S}$$$, glide your finger to key $$$\mathbf{K_2}$$$. it takes $$$\lvert 2 - 4 \rvert = 2$$$ additional seconds to glide the finger from index $$$4$$$ to index $$$2$$$. -
In order to type the third character
4of the string $$$\mathbf{S}$$$, glide your finger to key $$$\mathbf{K_1}$$$. it takes $$$\lvert 1 - 2 \rvert = 1$$$ additional second to glide the finger from index $$$2$$$ to index $$$1$$$. -
In order to type the fourth character
1of the string $$$\mathbf{S}$$$, glide your finger to key $$$\mathbf{K_2}$$$. it takes $$$\lvert 2 - 1 \rvert = 1$$$ additional second to glide the finger from index $$$1$$$ to index $$$2$$$. - We have typed all characters of the string $$$\mathbf{S}$$$ in a total of $$$4$$$ seconds.
In Additional Sample Case #2, we can take the following steps to type string $$$\mathbf{S}$$$ in minimum time.
-
Start by keeping your finger on key $$$\mathbf{K_4}$$$ which has character
1. We have now typed the first character of the string $$$\mathbf{S}$$$. -
In order to type the second character
2of the string $$$\mathbf{S}$$$, glide your finger to key $$$\mathbf{K_1}$$$. it takes $$$\lvert 1 - 4 \rvert = 3$$$ additional seconds to glide the finger from index $$$4$$$ to index $$$1$$$. -
In order to type the third character
3of the string $$$\mathbf{S}$$$, glide your finger to key $$$\mathbf{K_2}$$$. it takes $$$\lvert 2 - 1 \rvert = 1$$$ additional second to glide the finger from index $$$1$$$ to index $$$2$$$. - We have typed all characters of the string $$$\mathbf{S}$$$ in a total of $$$4$$$ seconds.
D. Suspects and Witnesses
Problem
Ada baked some cookies for her birthday party where she invited $$$\mathbf{N}$$$ guests, labeled $$$1$$$ to $$$\mathbf{N}$$$. When all the guests have arrived and the party is about to start, something terrible has happened — someone stole the cookies!
Ada puts on her detective hat and starts questioning her guests. She gathered $$$\mathbf{M}$$$ witness statements of the form: Guest x: "Guest y did not steal the cookies."
Ada knows that, if a guest is innocent (did not steal a cookie), then all their witness statements must be true. Note that Ada does not know whether any statement made by a cookie stealer is correct.
Lastly, Ada has an informant who told her there can be at most $$$\mathbf{K}$$$ cookie stealers. With this information, can you help Ada find out the number of guests who can be proved to be innocent?
Note that it is possible that no guest actually stole the cookies, and Ada simply forgot how many cookies she baked.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test
cases follow.
The first line of each test case contains three integers $$$\mathbf{N}$$$, $$$\mathbf{M}$$$, and $$$\mathbf{K}$$$:
the number of guests, the number of witness statements, and the maximum number
of cookie stealers, respectively.
The next $$$\mathbf{M}$$$ lines describe the witness statements. The $$$i$$$-th line
contains two integers $$$\mathbf{A_i}$$$ and $$$\mathbf{B_i}$$$, which means the witness statement
Guest $$$\mathbf{A_i}$$$: "Guest $$$\mathbf{B_i}$$$ did not steal the cookies."
Output
For each test case, output one line containing
Case #$$$x$$$: $$$y$$$, where $$$x$$$ is the test case number
(starting from 1) and $$$y$$$ is the number of guests that can be proved to be
innocent.
Limits
Time limit: 40 seconds.
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$2 \le \mathbf{N} \le 10^5$$$.
$$$1 \le \mathbf{M} \le 10^5$$$.
$$$1 \le \mathbf{A_i} \le \mathbf{N}$$$, for all $$$i$$$.
$$$1 \le \mathbf{B_i} \le \mathbf{N}$$$, for all $$$i$$$.
$$$\mathbf{A_i} \neq \mathbf{B_i}$$$, for all $$$i$$$.
$$$(\mathbf{A_i}, \mathbf{B_i}) \neq (\mathbf{A_j}, \mathbf{B_j})$$$, for all $$$i \neq j$$$.
Test Set 1
$$$\mathbf{K} = 1$$$.
Test Set 2
$$$1 \le \mathbf{K} \le 20$$$.
Sample
Note: there are additional samples that are not run on submissions down below.2 3 2 1 1 2 2 3 3 3 1 1 2 2 3 3 1
Case #1: 2 Case #2: 3
In Sample Case #1, there are $$$\mathbf{N}=3$$$ guests, $$$\mathbf{M}=2$$$ witness
statements and at most $$$\mathbf{K}=1$$$ cookie stealer.
The witness statements are:
- Guest $$$1$$$: Guest $$$2$$$ did not steal the cookies.
- Guest $$$2$$$: Guest $$$3$$$ did not steal the cookies.
Now we consider all possible arrangements on whether each guest is a cookie stealer.
| Guest 1 | Guest 2 | Guest 3 | Possible? | |
|---|---|---|---|---|
| Scenario #1 | Innocent | Innocent | Innocent | YES |
| Scenario #2 | CS | Innocent | Innocent | YES |
| Scenario #3 | Innocent | CS | Innocent | NO |
| Scenario #4 | Innocent | Innocent | CS | NO |
These are all the scenarios where there is at most $$$\mathbf{K}=1$$$ cookie stealer (CS). Scenario #3 is impossible because Guest 1 is innocent and states that Guest 2 is innocent, but Guest 2 turns out to be the cookie stealer. Same reasoning for scenario #4.
For the remaining scenarios, we see that Guest 2 and 3 are always innocent, so the answer is $$$2$$$.
Additional Sample - Test Set 2
The following additional sample fits the limits of Test Set 2. It will not be run against your submitted solutions.2 3 2 2 1 2 2 3 3 3 2 1 2 2 3 3 2
Case #1: 1 Case #2: 2
Analysis — A. Image Labeler
First, we need to understand how to obtain the median of a set. A median is the value separating the higher and lower halves of a set, so a set of length $$$k$$$ will have its median at element $$$k/2$$$. For sets with an even number of elements, the median is the average of the two middle elements.
A brute force approach to this problem is described in the example case, where we try each possible combination of assigning regions to categories, and taking the combination with the largest sum of medians.
Time complexity: $$$O(2^\mathbf{M})$$$ since we need to test each combination of either assigning a region or not to each category. We can reduce the time complexity even further through dynamic programming to avoid recalculating assignmented categories, but there is an even better approach.
A more efficient approach is to maximize the sum by ensuring that the largest regions each form their separate category. One way to do this is with a greedy approach, where we remove the single largest region (say $$$\mathbf{A_k}$$$) and assign it to a new category. Then the median of this category is equal to the size of that region. Note that this is the largest median that we can obtain, because all other regions $$$\mathbf{A_1},\cdots,\mathbf{A_N} \le \mathbf{A_k}$$$. If we continue this process for the next $$$\mathbf{N}-1$$$ categories, we will have the largest possible medians for all $$$\mathbf{N}$$$ regions. The largest regions can be identified by sorting $$$\mathbf{A}$$$ in descending order.
The problem is that we may run out of categories. Precisely, we still have $$$\mathbf{N}-\mathbf{M}$$$ regions that we need to assign to some categories. Since we know that for each of these remaining regions that they are smaller or equal to the ones already assigned to categories, then assigning a new region to an existing category may reduce the median of that category. We can decide to decrease the median of only one category — the one that already has the smallest median. Our result (the sum of medians) is then the sum of the largest $$$\mathbf{M}-1$$$ regions plus the median of all other regions.
Time complexity: $$$O(\mathbf{N} \log \mathbf{N}+\mathbf{M})$$$ since we need to sort $$$\mathbf{N}$$$ regions and sum up the top $$$\mathbf{M}-1$$$. Calculating the median of the final category is only $$$O(1)$$$ because the regions are already in sorted order. We can even solve this problem in linear time, but it was not required for this problem. We only need to find top $$$\mathbf{M}$$$-1 regions (and we can do it in $$$O(\mathbf{N} + \mathbf{M})$$$ time), and then we can find the median of the remaining regions in linear time as well.
Proof
We can formally prove that the greedy algorithm produces an optimal result.
We will prove that given any two arbitrary categories, the sum of medians does not decrease if we reassign the regions within these categories so that the largest region forms one category, and all the other regions forms the other category. Let $$$\{O_1, O_2\}$$$ denote these two arbitrary categories. Let $$$S$$$ denotes the number of participants in the region with the largest number of participants within these categories and $$$T = O_1 \cup O_2 \setminus \{S\}$$$ ($$${S}$$$ and $$$T$$$ are two categories produced by the greedy algorithm). We want to show that $$$median(O_1) + median(O_2) \leq S + median(T)$$$. Without loss of generality, let us assume that $$$median(O_1) \leq median(O_2)$$$. In the pictures below, let us assume that the regions within a category are sorted in the non-decreasing order.
In $$$T$$$, there are at least $$$\left\lceil\frac{|O_1|}{2}\right\rceil + \left\lceil\frac{|O_2|}{2}\right\rceil - 1$$$ regions larger than or equal to $$$median(O_1)$$$ — the regions larger than or equal to the medians of $$$O_1$$$ and $$$O_2$$$, but we need to remove $$$S$$$ (hence $$$-1$$$). Now we have to consider two cases:
- Either in $$$T$$$ there are at least $$$\left\lceil\frac{|O_1|}{2}\right\rceil + \left\lceil\frac{|O_2|}{2}\right\rceil$$$ regions larger than or equal to $$$median(O_1)$$$, which implies $$$median(T) \geq median(O_1)$$$, so we can say that $$$median(O_1) + median(O_2) \leq S + median(T)$$$, what we wanted to prove.
- There are exactly $$$\left\lceil\frac{|O_1|}{2}\right\rceil + \left\lceil\frac{|O_2|}{2}\right\rceil - 1$$$
regions larger than or equal to $$$median(O_1)$$$. Now we will once
again consider various cases depending on the parity of $$$|O_1|$$$ and $$$|O_2|$$$:
- $$$|O_1|$$$ and $$$|O_2|$$$ are even. Let us denote $$$L_1$$$ and $$$R_1$$$ as two "middle" regions of $$$O_1$$$ and
$$$L_2$$$ and $$$R_2$$$ as two "middle" regions of $$$O_2$$$.
- $$$|O_1|$$$ and $$$|O_2|$$$ are odd. Then we can see that there are $$$\left\lceil\frac{|O_1|}{2}\right\rceil + \left\lceil\frac{|O_2|}{2}\right\rceil$$$ regions with more participants than $$$median(O_1)$$$, which is the case that we already described above.
- One of $$$|O_1|$$$ and $$$|O_2|$$$ is even and the other one is odd. The argument here is similar to the arguments above, so we will leave it as an exercise to a reader.
- $$$|O_1|$$$ and $$$|O_2|$$$ are even. Let us denote $$$L_1$$$ and $$$R_1$$$ as two "middle" regions of $$$O_1$$$ and
$$$L_2$$$ and $$$R_2$$$ as two "middle" regions of $$$O_2$$$.
If you would like to explore more tasks like Image Label Verification on the Crowdsource app and directly train Google’s artificial intelligence systems to make Google products work equally well for everyone, everywhere, you can download it here.
Analysis — B. Maximum Gain
Test Set 1
One straightforward way to solve this problem is to simulate the process with a recursive brute force method. Let us define the following variables:
- $$$Ai$$$: The pointer to the start of array $$$\mathbf{A}$$$. The pointer moves one step ahead after answering the first question from $$$\mathbf{A}$$$, i.e. $$$Ai$$$ becomes $$$Ai+1$$$.
- $$$Aj$$$: The pointer to the end of array $$$\mathbf{A}$$$. The pointer moves one step back after answering the last question from $$$\mathbf{A}$$$, i.e. $$$Aj$$$ becomes $$$Aj-1$$$.
- $$$Bi$$$: The pointer to the start of array $$$\mathbf{B}$$$.
- $$$Bj$$$: The pointer to the end of array $$$\mathbf{B}$$$.
- $$$k$$$: The remaining number of questions to answer.
With these variables, we can write down the recursive equation as follows:
The maximum points we can get by answering $$$\mathbf{K}$$$ questions from arrays $$$\mathbf{A}$$$ and $$$\mathbf{B}$$$ would be the return value of $$$f(1, \mathbf{N}, 1, \mathbf{M}, \mathbf{K})$$$. Be careful that indexes $$$Ai$$$, $$$Aj$$$, $$$Bi$$$, and $$$Bj$$$ may go out of bounds of arrays $$$\mathbf{A}$$$ and $$$\mathbf{B}$$$. The out-of-bounds values are defined to be zeros in the equations above.
However, the time complexity of the recursion above is $$$O(4^\mathbf{K})$$$. To improve the performance, we can use dynamic programming: keep the return values in a 4-dimensional array to avoid repeated computation. Notice that the memoization array does not need to keep parameter $$$k$$$ since it can be derived from the other four parameters with $$$k=\mathbf{K}-(Ai -1)-(\mathbf{N}-Aj)-(Bi-1)-(\mathbf{M}-Bj)$$$. With memoization, the time complexity of this method is $$$O(\mathbf{K}^4)$$$, and space complexity is $$$O(\mathbf{K}^4)$$$.
Test Set 2
Notice that the order of questions to answer does not affect the points we get from them. Therefore, we can always answer questions in the first array $$$\mathbf{A}$$$ first, and then in the second array $$$\mathbf{B}$$$. This observation allows us to divide the problem into two sub-problems: find the maximum points $$$P_A$$$ we can get by answering $$$K_A$$$ questions in the first array $$$\mathbf{A}$$$, and the maximum points $$$P_B$$$ by answering $$$K_B$$$ questions in the second array $$$\mathbf{B}$$$. Enumerating all possible combinations of $$$(K_A, K_B)$$$ where $$$K_A + K_B = \mathbf{K}$$$, the total maximum points we can get by answering $$$\mathbf{K}$$$ questions would be the maximum value of all $$$P_A + P_B$$$.
Now we want to find a way to get the maximum points $$$P_A$$$ by answering $$$K_A$$$ questions in the first array $$$\mathbf{A}$$$. Since the order of questions to answer does not matter, we can answer $$$K_{AStart}$$$ questions from the start of the array first, and then $$$K_{AEnd}$$$ questions from the end of the array, such that $$$K_{AStart} + K_{AEnd} = K_A$$$. The points we get would be:
Therefore, we can find the maximum points $$$P_A$$$ by enumerating all combinations of $$$(K_{AStart}, K_{AEnd})$$$ where $$$K_{AStart} + K_{AEnd} = \min(K_A, \mathbf{N})$$$, and find the maximum values of all $$$P'_A$$$ with the equation aforementioned. With the prebuilt prefix sum and suffix sum arrays, we can get $$$P'_A$$$ in $$$O(1)$$$ time, and the maximum points $$$P_A$$$ in $$$O(K_A)$$$ time.
We can apply the same algorithm to find the maximum points $$$P_B$$$ by answering $$$K_B$$$ questions in the second array $$$\mathbf{B}$$$. The time complexity for this method would be:
- $$$O(\mathbf{N} + \mathbf{M})$$$ to prebuild the prefix and suffix arrays for $$$\mathbf{A}$$$ and $$$\mathbf{B}$$$.
-
$$$O(\mathbf{K}^2)$$$ to get the total maximum points.
- $$$O(1)$$$ to get the points with a pair $$$(K_{AStart}, K_{AEnd})$$$ or $$$(K_{BStart}, K_{BEnd})$$$.
- $$$O(\mathbf{K})$$$ to enumerate all $$$(K_{AStart}, K_{AEnd})$$$ pairs and get $$$P_A$$$ — maximum points by answering questions from array $$$\mathbf{A}$$$. Same for array $$$\mathbf{B}$$$.
- $$$O(\mathbf{K}^2)$$$ to enumerate all $$$(K_A, K_B)$$$ pairs and get the total maximum points.
- Overall: $$$O(\mathbf{K}^2 + \mathbf{N} + \mathbf{M})$$$.
If you would like to explore more tasks like Audio Validation and Image Labeler Tasks on the Crowdsource app and directly train Google's artificial intelligence systems to make Google products work equally well for everyone, everywhere, you can download it here.
Analysis — C. Touchbar Typing
Test Set 1
When there is no duplicate key in the keyboard, there is only one way to type any given string. It would suffice to simulate typing the given string and count the cost, for test set 1.
We can build a mapping from each character in the keyboard to its position in the keyboard. Let us denote the position of $$$i$$$-th character of $$$\mathbf{S}$$$ on the keyboard as $$$p_i$$$.
Let us denote the current position of the finger on the keyboard with $$$y$$$. We should start with the finger on the keyboard on $$$p_1$$$ position.
Then in each step, we need to add $$$\lvert y - p_i \lvert$$$ to the answer, and update the current keyboard position to $$$p_i$$$.
The time complexity of creating the mapping from each character to a position on the keyboard is $$$O(\mathbf{M})$$$ . With help of the mapping previously mentioned, the time complexity of calculating the answer is $$$O(\mathbf{N})$$$. The total time complexity of this approach is $$$O(\mathbf{N}+\mathbf{M})$$$, which is sufficient for test set 1.
Test Set 2
In test set 2, keys on the keyboard are not unique. At each step of typing, there might be multiple possible positions on the keyboards to move to next, and making optimal choice at every step will lead to the minimum number of moves.
Let us denote the set of positions of $$$i$$$-th character of $$$\mathbf{S}$$$ on the keyboard as $$$P_i$$$.
We can consider a dynamic programming approach, where for each position $$$x$$$ on the given string,
and each position $$$y$$$ on the keyboard, we need to find the optimal solution based on
possible options for that instance. Then we have the recurrent function $$$F$$$,
$$$F(x, y) = min(F(x-1, j) + \lvert(y-j)\lvert), j \in P_{x-1}$$$.
This approach gives us a time complexity of $$$O(\mathbf{N}\times\mathbf{M}\times\mathbf{M})$$$, as there are total $$$\mathbf{N}\times\mathbf{M}$$$ possible states, and on each state, there are at most $$$\mathbf{M}$$$ options in the worst case. This is sufficient for test set 2.
Test Set 3
For test set 3, $$$O(\mathbf{N}\times\mathbf{M}\times\mathbf{M})$$$ is not sufficient. We need to make the choices more carefully to reduce the complexity. Try to think a little on how to optimise this step before looking into the solution :)
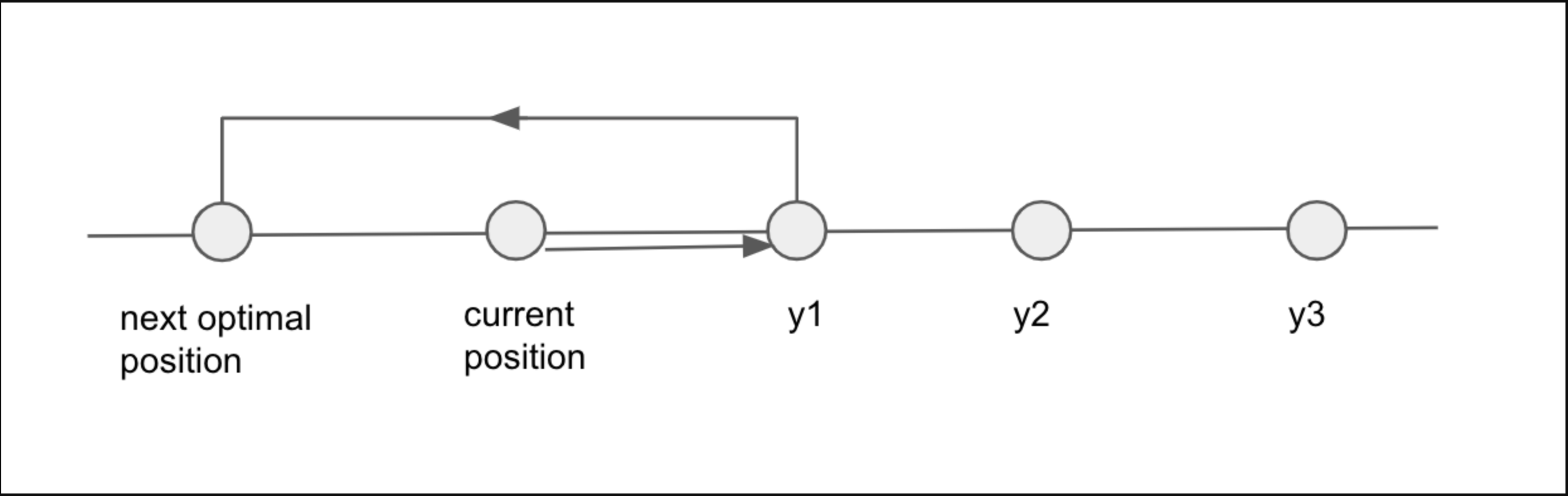
One interesting observation is that every time when there are multiple possible keyboard positions to jump to type the next character, it is always optimal to pick either the one with the minimal distance on the left direction, or the one with the minimal distance on the right direction. Let us consider the current position on the keyboard is $$$x$$$, and there are multiple possibilities on the right, denoted by $$$y_1$$$, $$$y_2$$$, $$$y_3$$$ and so on, sorted by in the order of increasing distance from $$$x$$$. Now, jumping to $$$y_2$$$ or $$$y_3$$$ cannot be a better choice than jumping to $$$y_1$$$. Let us consider two cases,
- The next optimal move lies in the opposite direction, aka left. Then it is better to jump
to the closest option $$$y_1$$$, to minimise the total distance.
- The next optimal move lies in the same direction, aka right. Then jumping to $$$y_1$$$ is at
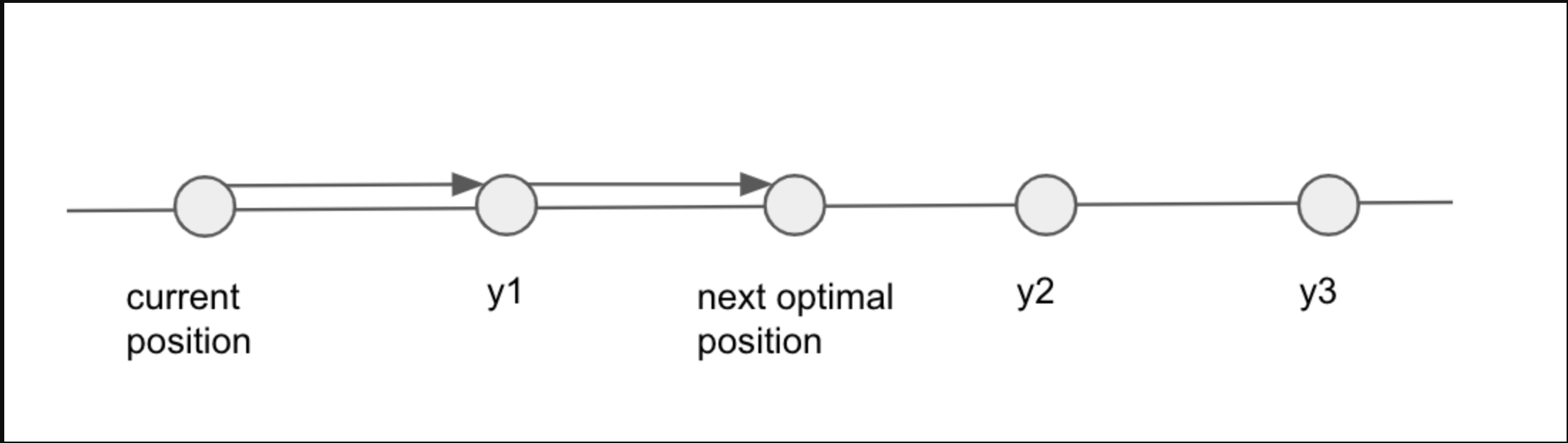
least not worse than jumping to $$$y_2$$$, $$$y_3$$$. It can even be a better option,
if the next optimal position lies between $$$y_1$$$ and $$$y_2$$$.
The same reasoning is
applicable in case of making a move to the left. Then it basically boils down to making a choice
of whether to move right, or left on the keyboard from any current position. The recurrent function
then changes to $$$F$$$,
$$$F(x, y) = min((F(x-1, j_{left}) + \lvert y-j_{left} \lvert), (F(x-1, j_{right}) + \lvert y-j_{right} \lvert))$$$
where $$${j_{left}, j_{right}} \in P_{x-1}$$$ and $$$j_{left}$$$ and $$$j_{right}$$$ are the closest two positions from $$$x$$$
on the left and the right respectively.
This makes the number of choices $$$O(1)$$$, giving us a total time complexity of $$$O(\mathbf{N}\times\mathbf{M})$$$, which is sufficient for test set 3.
If you would like to explore more tasks like Glide Type on the Crowdsource app and directly train Google’s artificial intelligence systems to make Google products work equally well for everyone, everywhere, you can download it here.
Analysis — D. Suspects and Witnesses
Let each suspect be a node in a graph $$$G$$$. If $$$A$$$ is a witness to $$$B$$$, then form a directed edge from $$$A$$$ to $$$B$$$.
It can be proven that a strongly connected component (SCC) $$$C$$$ in $$$G$$$ has the property that either:
- Everyone is innocent.
- Or everyone is a cookie stealer.
As a proof, if an arbitrary node $$$u$$$ is innocent, then, for every edge $$$e$$$ that goes from $$$u$$$ to $$$v$$$, node $$$v$$$ is also innocent. By induction, every node in $$$C$$$ is innocent. Similarly, if an arbitrary node $$$u$$$ is a cookie stealer, then every node $$$v$$$, where $$$(u,v)$$$ is an edge in $$$G$$$, is also a cookie stealer. By induction, every node in $$$C$$$ is a cookie stealer.
Given our graph $$$G$$$, we find all the SCC in $$$G$$$ and form a new graph $$$G'$$$ where:
- Each SCC in $$$G$$$ corresponds to a node in $$$G'$$$.
- Each node in $$$G'$$$ has a value $$$w$$$ which corresponds to the size of the SCC.
- If there exists an edge $$$(u,v)$$$ in $$$G$$$ and the two nodes do not share a SCC, there is an edge $$$(u', v')$$$ in $$$G'$$$ where $$$u'$$$ is the corresponding node for $$$u$$$ and $$$v'$$$ is the corresponding node for $$$v$$$.
You can form $$$G'$$$ in $$$O(|V| + |E|)$$$ using Tarjan's strongly connected components algorithm .
If there are at least $$$\mathbf{K}$$$ suspects that can reach node $$$u$$$ in $$$G$$$, then $$$u$$$ must be innocent.
To prove this, we use contradiction. If $$$u$$$ is a cookie stealer, then every node that can reach $$$u$$$ is a cookie stealer. Since there are at least $$$\mathbf{K}$$$ of them, this implies at least $$$\mathbf{K}+1$$$ cookie stealers which is a contradiction.
Hence, if a node $$$u$$$ in $$$G$$$ belongs to a SCC ($$$C_1$$$) of size larger than $$$\mathbf{K}$$$, that node must be an innocent person. Therefore, we can iterate over all nodes and check this. However, since a node can belong to a different component ($$$C_2$$$) from which $$$C_1$$$ is reachable, then we have to check the reachability of each node to other nodes.
We can go through all the nodes of $$$G'$$$ in topologically sorted order. We can go through all the neighbour nodes, i.e., nodes $$$v$$$ that have a directed edge from the current node $$$u$$$ to $$$v$$$ and, since $$$u$$$ is reachable to $$$v$$$, we can add $$$u$$$ to the set that belongs to $$$v$$$. Whenever a set reaches the size of $$$\mathbf{K}+1$$$, we can stop adding items to it. We will continue this process according to the topologically sorted order. Since we are going through all nodes (topologically), checking every edge at most once at the worst case and performing at most $$$\mathbf{K}+1$$$ insertions into the set, the overall time complexity for the method would be $$$O((\mathbf{N} + \mathbf{M})\mathbf{K}\log\mathbf{K})$$$. Once all nodes have been visited, we can go through all the nodes and count the number of nodes that have a reachability set of size is more than $$$\mathbf{K}$$$ which should take $$$O(\mathbf{N})$$$.
Therefore, the overall time complexity of this solution would be $$$O((\mathbf{N} + \mathbf{M})\mathbf{K}\log\mathbf{K})$$$. In terms of space complexity, we would require $$$O(\mathbf{N})$$$ for SCC construction and SCC graph construction. The space complexity of finding reachability sets will be $$$O(\mathbf{NK})$$$ since for every node we can have at most $$$\mathbf{K}+1$$$ nodes that we store. Therefore, the overall space complexity should be $$$O(\mathbf{NK})$$$.