Google Kick Start Archive — Round C 2022 problems

Test Set 1

For this test set, the old password only satisfies requirements $$$1$$$ and $$$4$$$. To satisfy other requirements, append a lowercase and an uppercase English alphabet letter and any special character at the end of the old password. These operations can be performed in any order. We can prove that this is the new password with minimum length satisfying all the requirements. The overall complexity of this solution is $$$O(N)$$$.

Sample Code (C++)

string createNewPassword(string oldPassword) {
    string newPassword = oldPassword;
    newPassword.append("a"); // Append any lowercase English alphabet letter.
    newPassword.append("B"); // Append any uppercase English alphabet letter.
    newPassword.append("&"); // Append any special character.

    return newPassword;
}

Test Set 2

To solve this test set, we can loop through the old password and check which of the given requirements are unsatisfied. For each unsatisfied requirements between $$$2$$$ and $$$5$$$ (both inclusive), we can just insert respective character and make it satisfied. After performing these operations, if the length of the new password is less than $$$7$$$, then we can append digits, letters, or special characters until the new password's length becomes $$$7$$$. We can prove that this is the new password with minimum length satisfing all the requirements. The time complexity of this solution is $$$O(N)$$$.

Sample Code (C++)

string createNewPassword(string oldPassword) {
    bool condition2 = false;
    bool condition3 = false;
    bool condition4 = false;
    bool condition5 = false;
    string newPassword = oldPassword;
    for (int i = 0; i < oldPassword.size(); i++) {
        if (oldPassword[i] >= 'A' && oldPassword[i] <= 'Z')
          condition2 = true;
        else if (oldPassword[i] >= 'a' && oldPassword[i] <= 'z')
          condition3 = true;
        else if (oldPassword[i] >= '0' && oldPassword[i] <= '9')
          condition4 = true;
        else if (oldPassword[i] == '@' || oldPassword[i] == '#' || oldPassword[i] == '&' || oldPassword[i] == '*')
          condition5 = true;
    }

    if (!condition2) newPassword.append("A"); // Append any uppercase English alphabet letter.
    if (!condition3) newPassword.append("a"); // Append any lowercase English alphabet letter.
    if (!condition4) newPassword.append("1"); // Append any digit.
    if (!condition5) newPassword.append("#"); // Append any special character.

    // Append any digit, letter, or a special character.
    while (newPassword.size() < 7) newPassword.append("1");

    return newPassword;
}

Let us simplify the problem statement. The problem is to partition '$$$\mathbf{N}$$$', the set of first $$$\mathbf{N}$$$ positive integers ($$$1, 2, \dots, \mathbf{N}$$$) into two subsets, $$$S_{Alan}$$$ and $$$S_{Barbara}$$$ (for Alan and Barbara), with $$$A$$$ and $$$B$$$ as their sums respectively, such that $$$\frac{A}{B}=\frac{\mathbf{X}}{\mathbf{Y}}$$$ and $$$A+B=\frac{\mathbf{N}(\mathbf{N}+1)}{2}$$$ (where $$$\frac{\mathbf{N}(\mathbf{N}+1)}{2}$$$ is the sum of first $$$\mathbf{N}$$$ positive integers , let us call it $$$Sum_N$$$).

Test Set 1

We can check all the possible partitions of '$$$\mathbf{N}$$$' into two subsets $$$S_{Alan}$$$ and $$$S_{Barbara}$$$ (where $$$S_{Alan}$$$ is non-empty), to see if we encounter a partition where $$$\frac{A}{B}=\frac{\mathbf{X}}{\mathbf{Y}}$$$. If we encounter such a partition, we can conclude that it is POSSSIBLE to partition '$$$\mathbf{N}$$$' as it is asked in the problem statement, and return this partition as the answer. If no such partition is encountered, we can conclude that the answer is IMPOSSIBLE.

Since there are $$$2^\mathbf{N}-1$$$ ways we can partition '$$$\mathbf{N}$$$' this way, and each partition takes $$$O(N)$$$ time to check for the conditions mentioned in the problem statement. The time complexity of this solution is $$$O(2^\mathbf{N} \times N)$$$.

Test Set 2

Since $$$A=Sum_N \times (\frac{\mathbf{X}}{\mathbf{X}+\mathbf{Y}})$$$ and $$$B=Sum_N \times (\frac{\mathbf{Y}}{\mathbf{X}+\mathbf{Y}})$$$. For $$$A$$$ and $$$B$$$ to be integers, $$$Sum_N\pmod{(\mathbf{X}+\mathbf{Y})}\equiv\mathbf{0}$$$. If $$$Sum_N\pmod{(\mathbf{X}+\mathbf{Y})}\not\equiv\mathbf{0}$$$ then it is IMPOSSIBLE to partition '$$$\mathbf{N}$$$' into $$$S_{Alan}$$$ and $$$S_{Barbara}$$$.

In what follows we will use a Greedy algorithm to form $$$S_{Alan}$$$. The proof that such a partition is always POSSIBLE if $$$Sum_N\pmod{(\mathbf{X}+\mathbf{Y})}\equiv\mathbf{0}$$$, can be given by mathematical induction.

Algorithm

Let us define a function def partition(N, PartitionSum) which returns a partition from the set of first $$$\mathbf{N}$$$ positive integers which sums up to the PartitionSum.

  def partition(N, PartitionSum):
    assert(N >= 0 and PartitionSum >= 0)
    if (PartitionSum == 0 or N == 0):
      return []
    // Greedily pick that largest available number to form the PartitionSum.
    if(N > PartitionSum):
      return partition(N-1, PartitionSum)
    else
      return [N] + partition(N-1, PartitionSum-N)

Proof by Induction

Base case

Given '$$$\mathbf{N}$$$', the set of first $$$\mathbf{N}$$$ positive integers. For $$$\mathbf{N}=1$$$, the possible values of $$$PartitionSum = [0,1]$$$. We can see that the algorithm works correctly, as it returns an empty set for $$$PartitionSum=0$$$, and greedily chooses $$$[1]$$$ from the set for $$$PartitionSum=1$$$.

Inductive Step

We want to show that if partitions can be formed greedily for $$$\mathbf{N}=K-1$$$ and $$$PartitionSum=[0,1,2,\dots,Sum_{K-1}]$$$ using the algorithm mentioned above, then the partitions can also be formed in the same way for $$$\mathbf{N}=K$$$ and $$$PartitionSum=[0,1,2,\dots,Sum_K]$$$.

Assume the induction hypothesis that we can form partitions greedily for $$$\mathbf{N}=K-1$$$ and $$$PartitionSum=[0,1,2,\dots,Sum_{K-1}]$$$ using the above algorithm, and a partition is denoted by partition(K-1,PartitionSum).

For $$$\mathbf{N}=K$$$, possible values of $$$PartitionSum$$$ are $$$PartitionSum=[0,1,2,\dots,Sum_K]$$$.

Now say, for the case when $$$K \le PartitionSum \le Sum_K$$$, to form the partition, we can greedily select $$$[K]$$$ and merge it with partition(K-1,PartitionSum-K). This is possible because $$$PartitionSum - K \le Sum_{K-1}$$$, so we know partition(K-1,PartitionSum-K) exists (our assumption from the inductive step).

Now for the other case when, $$$0 \le PartitionSum \lt K$$$, we can choose partition(K-1,PartitionSum) to form this partition as $$$K-1 \le Sum_{K-1}$$$, hence partition(K-1,PartitionSum) exists (our assumption from the inductive step).

Since, both the Base case and Inductive Step have been proven as true, by mathematical induction the greedy algorithm mentioned above works for every $$$\mathbf{N}$$$ and $$$PartitionSum=[0,1,2,\dots,Sum_N]$$$.

We can use the above algorithm to form $$$S_{Alan}$$$ by calling partition(N, A), what remains after picking elements for $$$S_{Alan}$$$, would be $$$S_{Barbara}$$$, as $$$A+B=Sum_N$$$. The time complexity of this algorithm is $$$O(N)$$$.

Background

The original "Ants on a Stick" is a well-known math question. The insight is that two identical ants bouncing off each other can be thought simply as the ants passing through each other.

Test Set 1

Limits are small in Test Set 1 so we can perform a simulation. First, we create an array of length $$$2\mathbf{L}$$$ as the stick - each unit is 0.5 cm. The reason we split into 0.5 cm instead of 1 cm is to simplify collision that happens on half a cm. Also note that one position may have 2 ants when the collision happens, so take that into account for your array data structure.

Then, place the ants on their respective starting positions. Now, we start to simulate with each iteration being half a second.

Look at each position starting from the left, if there exists some ants, there are 3 cases to handle.

1. If the ant is going to fall off (facing left on leftmost position or facing right on rightmost position), note down its ID and current time (iteration count), then remove it.
2. If there is only one ant in that position, move it one unit according to its direction.
3. If there are two ants in that position, reverse their direction and move it one unit according to its new direction.

Implementation tip: Use a new array to simulate the next iteration instead of modifying in-place. This makes it easier to understand and debug.

When there are no ants left on the stick, we sort the ants first by the time they fall, and then their ID.

The time complexity for this solution is $$$O(\mathbf{L}^2)$$$, as we need $$$O(\mathbf{L})$$$ time for each iteration and there are at most $$$O(\mathbf{L})$$$ iterations.

The space complexity for this solution is also $$$O(\mathbf{L}^2)$$$ if you use a new array for each iteration, but can reduce to $$$O(\mathbf{L})$$$ by reusing the arrays. We keep just two arrays - $$$A_{current}$$$ for the current iteration and $$$A_{next}$$$ for the next iteration. Once an iteration is completed, we copy $$$A_{next}$$$ into $$$A_{current}$$$ and clear the content of $$$A_{next}$$$.

Test Set 2

For Test Set 2, $$$\mathbf{L}$$$ gets too large so our previous solution will not work. We will now make use of the "pass-through" property discussed in the background section. Think of each ant initially having their own ID card. Instead of bouncing off and changing direction, they actually just exchange ID cards and politely pass through each other. With this observation, the problem becomes finding the order of ants falling and reporting the ID card they possess at that time.

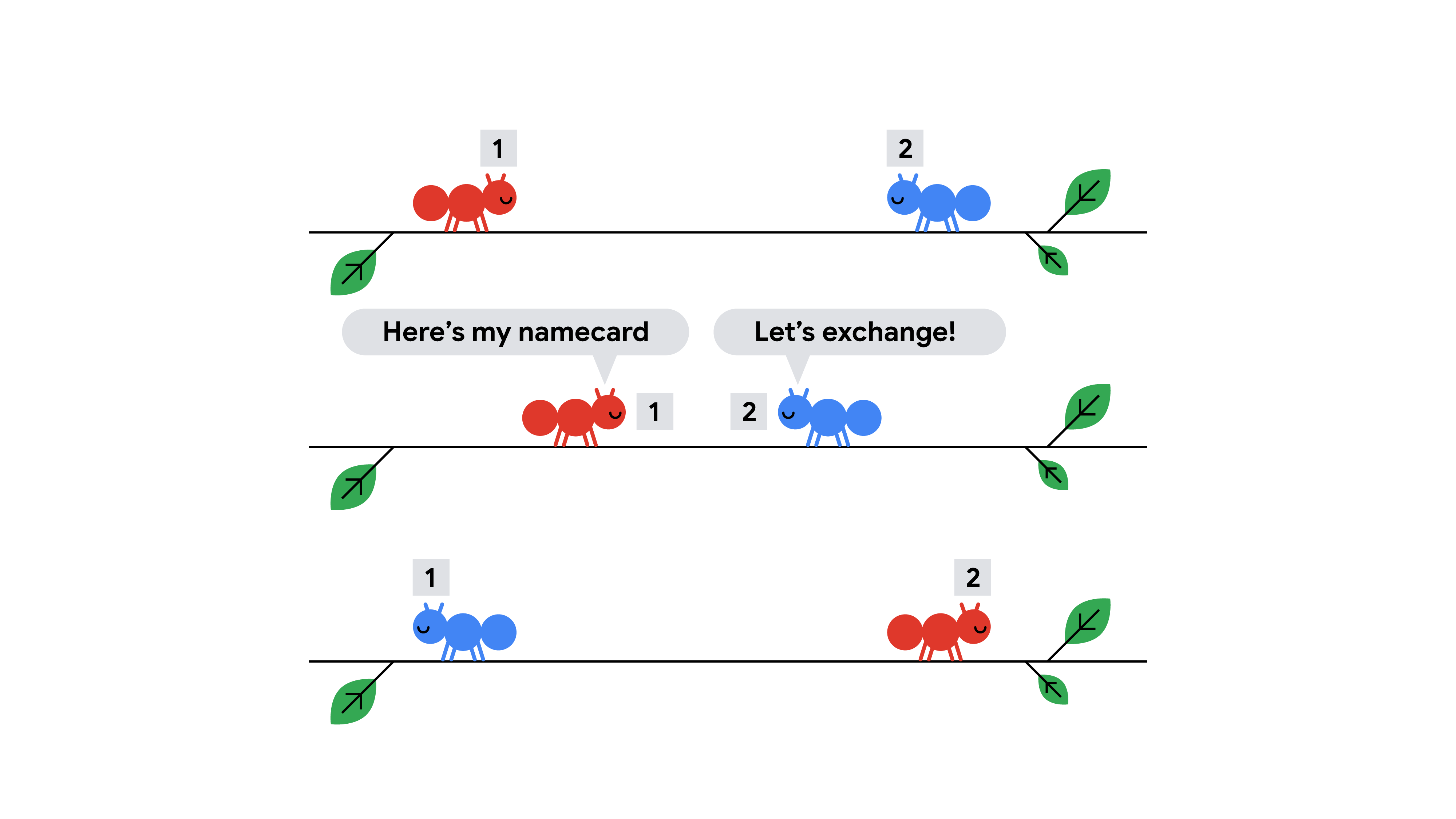
Now we want to find all events of exchanging ID cards. An event is defined by $$$(x_1, x_2, t)$$$, meaning $$$x_1$$$ and $$$x_2$$$ exchange ID cards at time $$$t$$$. For an ant $$$x$$$ facing right, the ants which $$$x$$$ will exchange ID cards with are all those on the right of $$$x$$$ and are facing left.

Once we have all the events of exchanging ID cards, we will sort them according to the time it happens. Suppose there are 2 ants that will exchange ID cards - $$$x_1$$$ with starting position $$$\mathbf{P_1}$$$ facing right, and $$$x_2$$$ with starting position $$$\mathbf{P_2}$$$ facing left. The time of the exchange is $$$(\mathbf{P_2}-\mathbf{P_1}) / 2$$$ seconds. Once we have the order of events, we will process each of them, by using an appropriate data structure (hash map or array with index as key) to keep track of the ID card possessed by each ant. Finally, we will have the ID cards of each ant of the time they fall off the stick.

Our last piece is to figure out the order of ants falling. This is relatively straightforward. For an ant facing left with starting position $$$\mathbf{P_1}$$$, the time of falling is $$$\mathbf{P_1}$$$. For an ant facing right with position $$$\mathbf{P_2}$$$, the time of falling is $$$\mathbf{L}-\mathbf{P_2}$$$. Finally, print out the ID cards of the ants in this order.

The time complexity for this solution is $$$O(\mathbf{N}^2\log \mathbf{N})$$$ to find all the events of exchanging cards and sorting them.

Test Set 3

For Test Set 3, the additional observation is that just by the fact that there is an ant falling off the left end of the stick, we know it must be the current leftmost ant that is still on the stick. No exchanges of ID cards.

For each ant, using the pass-through property, find the time it falls off the stick and in which direction. In the end we should have an array of length $$$\mathbf{N}$$$ of $$$(t,d)$$$, meaning the time and the direction an ant falls off.

Finally, sort the ants by their starting position, and the fall off events by their time. For each fall off event, if it is on the left end, we print the ID of the leftmost ant and remove it, and vice versa for fall off event on the right end.

The time complexity for this solution is $$$O(\mathbf{N}\log \mathbf{N})$$$.

The expected value of a discrete random variable is defined as the weighted average over all possible values of the variable. That is, for a discrete random variable $$$X$$$ with probability function $$$P(X)$$$, its expected value $$$E[X] = $$$ the sum of $$$X \times P(X)$$$ over all possible values of $$$X$$$.

Keeping the above definition in mind, we can define a random variable $$$X$$$ as the number of palindromes encountered in a particular game of Palindromic Deletions on a string of length $$$\mathbf{N}$$$, with $$$P(X)$$$ being the probability function. We can write $$$P(X) = \frac{A(X)}{B}$$$, where $$$A(X)$$$ is the number of distinct games which generate $$$X$$$ palindromes and $$$B$$$ is the total number of distinct games. Notice that the number of distinct games can be defined as the total number of orders of picking indexes $$$1$$$ to $$$\mathbf{N}$$$, which is equivalent to to the number of permutations of an array of size $$$\mathbf{N}$$$. Therefore, $$$B = \mathbf{N}!$$$.

With the above simplification, we can write the expected value $$$E[X] = $$$ the sum of $$$\frac{X \times A(X)}{\mathbf{N}!}$$$ over all possible integer values of $$$X$$$ between $$$1$$$ and $$$\mathbf{N}$$$. Note that the game counts an empty string as a palindrome, hence it is not possible for $$$X$$$ to be $$$0$$$. The problem translates into calculating the sum of $$$X \times A(X)$$$ over all $$$X$$$ under modulo $$$10^{9} + 7$$$ (let us call this value $$$Y$$$). We can then multiply $$$Y$$$ by the modular inverse of $$$\mathbf{N}!$$$ under modulo $$$10^{9} + 7$$$ to get $$$E[X]$$$. Note that we are able to simply multiply by the modular inverse of $$$\mathbf{N}!$$$ modulo $$$10^{9} + 7$$$ without reducing the fraction to an irreducible form since $$$10^{9} + 7$$$ is prime and $$$\mathbf{N} \le 400$$$, which gives us $$$\gcd (\mathbf{N}!, 10^{9} + 7) = 1$$$ (as the denominator will not contain any prime factors $$$ \gt 400 $$$).

Test Set 1

For $$$\mathbf{N} \le 8$$$, we can simply recursively generate all possible games to calculate $$$Y$$$. One way to do this is by starting with the input string and a count of palindromes encountered $$$cnt = 0$$$. In each recursion level, we delete a character from the string and check if the new string is a palindrome. If the new string is a palindrome, we increase $$$cnt$$$ by $$$1$$$. We recursively do this operation again with the new string and $$$cnt$$$. This is done for each character in the string at a particular recursion level. We return when we reach an empty string, at which point we add $$$cnt$$$ to an outer $$$sum$$$ variable. After the top level recursive function returns, $$$sum$$$ will store the value $$$Y$$$. All operations are done under modulo $$$10^9 + 7$$$.

For example, let us visualize this with the sample string $$$aba$$$.

1. "aba", $$$0 \rightarrow $$$ "ba", $$$0 \rightarrow $$$ "a", $$$1 \rightarrow $$$ "", $$$2$$$
2. "aba", $$$0 \rightarrow $$$ "ba", $$$0 \rightarrow $$$ "b", $$$1 \rightarrow $$$ "", $$$2$$$
3. "aba", $$$0 \rightarrow $$$ "aa", $$$1 \rightarrow $$$ "a", $$$2 \rightarrow $$$ "", $$$3$$$
4. "aba", $$$0 \rightarrow $$$ "aa", $$$1 \rightarrow $$$ "a", $$$2 \rightarrow $$$ "", $$$3$$$
5. "aba", $$$0 \rightarrow $$$ "ab", $$$0 \rightarrow $$$ "b", $$$1 \rightarrow $$$ "", $$$2$$$
6. "aba", $$$0 \rightarrow $$$ "ab", $$$0 \rightarrow $$$ "a", $$$1 \rightarrow $$$ "", $$$2$$$

Adding all $$$cnt$$$ at the end of each simulation, we get $$$sum = 2 + 2 + 3 + 3 + 2 + 2 = 14$$$. Hence, we get an expected value of $$$\frac{14}{3!} = \frac{14}{6}$$$. Dividing 14 and 6 by their GCD (greatest common divisor) i.e. $$$2$$$, we get the irreducible fraction $$$\frac{7}{3}$$$.

The number of orders generated is $$$\mathbf{N}!$$$, while it takes $$$O(\mathbf{N})$$$ to check if a string is a palindrome. The time and space complexity comes out to be $$$O(\mathbf{N} \times \mathbf{N}!)$$$, which is approximately $$$3 \times 10^5$$$ operations.

Test Set 2

Instead of thinking about $$$Y$$$ as the sum of $$$X \times A(X)$$$, where $$$A(X)$$$ is the number of games that generate $$$X$$$ palindromes, we can conversely think about it as the sum of $$$Q(K)$$$ over all $$$K = 0$$$ to $$$\mathbf{N} - 1$$$, where $$$Q(K)$$$ is the number of games in which a palindrome of length $$$K$$$ is encountered.

Another observation to make here is that any palindrome that we encounter in a game will be a subsequence of the input string $$$\mathbf{S}$$$. Consider a palindrome of length $$$K$$$ that exists as a subsequence of the input string $$$\mathbf{S}$$$. The number of games in which we will encounter this palindrome is $$$K! \times (\mathbf{N} - K)!$$$. This is because to encounter a particular palindrome of length $$$K$$$ in a game, we must first remove the $$$\mathbf{N} - K$$$ characters that are not part of the palindrome in any order, then remove the remaining $$$K$$$ characters in any order. With this, we get $$$Q(K) = K! \times (\mathbf{N} - K)! \times F(K)$$$, where $$$F(K)$$$ is the number of palindromes of length $$$K$$$ that occur as a subsequence of $$$\mathbf{S}$$$.

All that remains is to find the number of palindromes of length $$$K$$$ that occur as a subsequence of $$$\mathbf{S}$$$. We can use dynamic programming to do this. We define our state as $$$(L, R, len)$$$, where the value of this state $$$DP(L, R, len)$$$ equals the number of palindromes of length $$$len$$$ that can be found as a subsequence of the substring $$$\mathbf{S}[L, R]$$$ (indices $$$L$$$ and $$$R$$$ inclusive). We have three base cases:

Now to calculate $$$DP(L, R, len)$$$, notice that if $$$\mathbf{S}[L] = \mathbf{S}[R]$$$, then we have $$$DP(L + 1, R - 1, len - 2)$$$ palindromes that have $$$\mathbf{S}[L]$$$ and $$$\mathbf{S}[R]$$$ as the first and last character respectively (or $$$DP(L + 1, R - 1, len - 1)$$$ palindromes if $$$L = R$$$). All remaining palindromes can be found as a union of the palindromes of length $$$len$$$ found in substrings $$$\mathbf{S}[L, R - 1]$$$ and $$$\mathbf{S}[L + 1, R]$$$. By the inclusion-exclusion principle, the value of this union comes out to be $$$DP(L, R - 1, len) + DP(L + 1, R, len) - DP(L + 1, R - 1, len)$$$. We subtract the palindromes found in $$$DP(L + 1, R - 1, len)$$$ as we would be double counting them in $$$DP(L, R - 1, len)$$$ and $$$DP(L + 1, R, len)$$$. The figure below helps visualize $$$DP(1, 4, 2)$$$ for string $$$abccbd$$$. Strings are zero indexed.

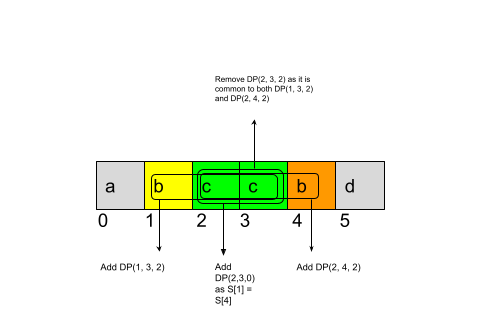
With the above defined state and DP calculation in mind, we get $$$F(K) = DP(0, \mathbf{N} - 1, K)$$$ and $$$Q(K) = DP(0, \mathbf{N} - 1, K) \times K! \times (\mathbf{N} - K)!$$$. Finally, we get $$$Y$$$ by summing all $$$Q(K)$$$ for $$$K = 0$$$ to $$$\mathbf{N} - 1$$$.

We can precompute factorials upto $$$400$$$ linearly, then subsequently retrieve the precomputed factorial values in constant time. The time to compute all states of the DP is $$$O(\mathbf{N}^3)$$$. Similarly, we have $$$\mathbf{N}^3$$$ integer DP states, giving us an overall time and space complexity of $$$O(\mathbf{N}^3)$$$.

Bonus Solution

While the above approach is good enough to pass the constraints if the DP array uses 32-bit integers, we can further optimize on space by optimizing the calculation for $$$F(K)$$$ for each $$$K$$$. Instead of creating an $$$\mathbf{N} \times \mathbf{N} \times \mathbf{N}$$$ DP array, we can create three $$$\mathbf{N} \times \mathbf{N}$$$ DP arrays, where the first corresponds to some palindrome length $$$len$$$, the second corresponds to length $$$len - 1$$$ and the third corresponds to length $$$len - 2$$$. As the transitions described in the previous approach for the DP values of a given length $$$len$$$ just need DP values from $$$len - 1$$$ and $$$len - 2$$$, we can construct the DP array for $$$len$$$ using DP values of $$$len - 1$$$ and $$$len - 2$$$, then construct the DP array for $$$len + 1$$$ using values from $$$len$$$ and $$$len - 1$$$, then for $$$len + 2$$$ using values from $$$len + 1$$$ and $$$len$$$, and so on. In this way, we can start with DP arrays for $$$len = 0$$$ and $$$1$$$ as base cases and iteratively construct for each $$$len = 2$$$ to $$$\mathbf{N} - 1$$$. The rest of the idea is similar to the previous solution. With this approach, even though the time complexity is still $$$O(\mathbf{N}^3)$$$, the space complexity comes down to $$$O(\mathbf{N}^2)$$$.