Google Kick Start Archive — Round A 2022 problems

For better understanding, let us define some variables:
$$$N$$$: Length of string $$$\mathbf{I}$$$
$$$M$$$: Length of string $$$\mathbf{P}$$$

Test Set 1

All the characters in String $$$\mathbf{I}$$$ are the same, let us say that character is $$$C$$$. This means that $$$\mathbf{I}$$$ is made up entirely of character $$$C$$$ occurring $$$N$$$ times.
We need to check if $$$\mathbf{P}$$$ contains $$$C$$$ at least $$$N$$$ number of times (recall that $$$N$$$ denotes the length of string $$$\mathbf{I}$$$). This can be done by simply maintaining a count of $$$C$$$ in $$$\mathbf{P}$$$. If this count is greater than or equal to $$$N$$$, then the number of characters to be removed would be $$$(M - N)$$$, which is the number of extra characters in $$$\mathbf{P}$$$. Else, the answer is IMPOSSIBLE.

Time and Space Complexity: All operations including counting the appearances of $$$C$$$ in $$$\mathbf{P}$$$ can be done in $$$O(M)$$$ time, which is the overall time complexity of this solution. Extra space required would be of the order of $$$O(1)$$$.

Test Set 2

Observe that we are trying to condense $$$\mathbf{P}$$$ to $$$\mathbf{I}$$$ by deleting some characters from $$$\mathbf{P}$$$ without disturbing their order. This directly leads us to the definition of a subsequence:
A subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements.

• If $$$\mathbf{I}$$$ is not a subsequence of $$$\mathbf{P}$$$, the answer is IMPOSSIBLE. This can take place when:

  • Case 1: $$$\mathbf{P}$$$ is shorter than $$$\mathbf{I}$$$

  • Case 2: A character in $$$\mathbf{I}$$$ is not present in $$$\mathbf{P}$$$

  • Case 3: A character in $$$\mathbf{I}$$$ is present in $$$\mathbf{P}$$$, but not at the right place

• If $$$\mathbf{I}$$$ is a subsequence of $$$\mathbf{P}$$$, then $$$\mathbf{P}$$$ contains all characters of $$$\mathbf{I}$$$ in the same order along with some extra characters (possibly $$$0$$$). Barbara will have to hit backspace on these extra characters to correct the string. The answer would be $$$(M - N)$$$.

Time and Space Complexity: Subsequence check can be done in $$$O(M)$$$ time using a two-pointer approach. The overall time complexity of this solution comes out to be $$$O(M)$$$ as well. Extra space required would be of the order of $$$O(1)$$$.

Pseudocode for Subsequence Check:

FUNCTION checkSubSequence(String I, String P) RETURNS BOOLEAN

    // Assign lengths of I and P to variables N and M
    N <- Length of I
    M <- Length of P

    // Declare pointers ptrI and ptrP to the current position in I and P respectively
    // and assign them to position 0
    ptrI <- 0
    ptrP <- 0

    // Traverse both strings, and compare current character of P with first unmatched char of I
    // While making sure the pointers do not go out of bounds of their respective strings
    WHILE ptrI is less than N AND ptrP is less than M

        // If characters at current positions match, then move ahead in both I and P
        IF I[ptrI] equals P[ptrP]
          ptrI <- ptrI + 1
          ptrP <- ptrP + 1

        // If the characters at current the positions do not match, then move ahead only in P
        ELSE
          ptrP <- ptrP + 1

        ENDIF

    ENDWHILE


    // If we reach past the end of I, we have successfully matched all the characters of I
    // to some characters of P
    // If not, some characters in I remain unmatched and it is not a subsequence of P
    IF ptrI equals N
      RETURN True;

    ELSE
      RETURN False;

    ENDIF

ENDFUNCTION

For simplicity, let us use $$$L$$$ to represent the number of digits in $$$\mathbf{N}$$$, note the scale of $$$L$$$ is actually $$$O(log_{10}\mathbf{N})$$$. And let us use $$$\{a_{L-1}, a_{L-2}, \dots , a_1, a_0\}$$$ to represent the digits of $$$\mathbf{N}$$$, where $$$a_{L-1}$$$ is the most significant digit and $$$a_0$$$ is the least significant digit ($$$0 \le a_i \le 9$$$ for all $$$i \lt L-1$$$, and $$$1 \le a_{L-1} \le 9$$$). We can read $$$\mathbf{N}$$$ as a string, where the characters in the string $$$\{s[0], s[1], \dots, s[L-2], s[L-1]\}$$$ represent $$$\{a_{L-1}, a_{L-2}, \dots , a_1, a_0\}$$$. Or, we can read $$$\mathbf{N}$$$ as an integer, whose value equals $$$a_{L-1} \times 10^{L-1}+ a_{L-2} \times 10^{L-2} + \cdots +a_1 \times 10 + a_0$$$. Inserting a new digit $$$d$$$ in the $$$k-$$$th position in $$$\mathbf{N}$$$ means inserting it after the first $$$L-k$$$ digits (on the left side) and before the last $$$k$$$ digits (on the right side) of $$$\mathbf{N}$$$. If $$$\mathbf{N}$$$ is string type, then the new number can be built by slicing and concatenating the string as $$$s[0 \dots L-k] + string(d) + s[L-k \dots L]$$$ in linear time, where $$$s[i \dots j]$$$ means characters of string $$$s$$$ from index $$$i$$$ to index $$$j$$$. On the other hand, if $$$\mathbf{N}$$$ is integer type, then the new number can be calculated as $$$(\mathbf{N}-\mathbf{N} \% 10^k)\times 10 + d\times 10^k + (\mathbf{N} \% 10^k)$$$ in constant time.

Test Set 1

Since $$$\mathbf{N} \le 10^5$$$, the number of digits of $$$\mathbf{N}$$$ is at most $$$6$$$, which means there are at most $$$7$$$ positions to insert a new digit. As for the new digit, there are at most $$$10$$$ options (0 $$$\dots$$$ 9), therefore the total number of results is at most $$$70$$$. We can enumerate all these $$$70$$$ results, eliminate those ones which are not multiples of $$$9$$$ or have leading zeros, then find the smallest one from them.

In this solution, there are $$$O(L)$$$ positions to insert a new digit, and a constant number of choices for the new digit (0 $$$\dots$$$ 9). If $$$\mathbf{N}$$$ is read as an integer, then we need constant time to insert a new digit, decide if the inserted result is a multiple of $$$9$$$ and compare the candidates, so the time complexity of this solution is $$$O(L)$$$. If $$$\mathbf{N}$$$ is read as a string, then every operation such as the insertion of a new digit or value comparison among candidates will take $$$O(L)$$$ time, so the time complexity will be $$$O(L^2)$$$.

Test Set 2

Now that $$$\mathbf{N}$$$ is at most $$$10^{123456}$$$, we cannot read $$$\mathbf{N}$$$ as 32-bit/64-bit integer. Instead, we should read $$$\mathbf{N}$$$ as string where each character represents a digit of $$$\mathbf{N}$$$. Since $$$L$$$ is at most $$$123456+1$$$, the brute force enumeration method with time complexity $$$O(L^2)$$$ is unacceptable. We need a more efficient algorithm.

First, let us decide which digit to insert. In fact, a number is a multiple of $$$9$$$ if and only if the sum of its all digits is a multiple of $$$9$$$. Therefore, we can add up all the $$$L$$$ digits of the given $$$\mathbf{N}$$$, and use $$$9-(sum \enspace mod \enspace 9)$$$ to get the new digit we want. Wherever we insert it, the sum of all digits of the new number and the new number itself will be a multiple of $$$9$$$. Note that when $$$sum \enspace mod \enspace 9=0$$$, adding either a new $$$0$$$ or a new $$$9$$$ can make the result be a multiple of $$$9$$$, but $$$0$$$ is always more preferable than $$$9$$$ because we are looking for the smallest answer.

Secondly, let us decide where to insert the new digit. Let us use $$$d$$$ to represent the new digit we are going to insert. We can start from the most significant digit $$$a_{L-1}$$$, then $$$a_{L-2}$$$, and then use this order to visit all the digits in $$$\mathbf{N}$$$, to find the first digit in $$$\mathbf{N}$$$ that is larger than $$$d$$$. Then we should insert $$$d$$$ right before this digit. In other words, say $$$a_k$$$ is the first digit in $$$\mathbf{N}$$$ that is larger than $$$d$$$ (i.e. $$$a_i \le d$$$ for all $$$k+1 \le i \le L-1$$$), then the new number we are going to make is $$$\{a_{L-1}, a_{L-2}, \dots, a_{k+1}, d, a_k, \dots, a_0\}$$$, whose value equals to $$$N_g = a_{L-1} \times 10^{L}+ a_{L-2} \times 10^{L-1} + \cdots + a_{k+1} \times 10^{k+2} + d \times 10^{k+1} + a_k \times 10^k + \cdots +a_0$$$.

Is this always the best choice? Yes, let us prove it. If we insert $$$d$$$ to a more significant position, i.e. between $$$a_{q+1}$$$ and $$$a_q$$$ where $$$q>k$$$, then the new number we are going to make is $$$\{a_{L-1}, a_{L-2}, \dots, a_{q+1}, d, a_q, \dots, a_k, \dots, a_0\}$$$ with value $$$N_o = a_{L-1} \times 10^{L}+ a_{L-2} \times 10^{L-1}+ \cdots +a_{q+1} \times 10^{q+2} + d \times 10^{q+1} + a_q \times 10^q + \cdots a_k \times 10^k + \cdots +a_0$$$. The difference between this solution and the solution we claimed is $$$N_o-N_g=d \times 10^{q+1}-9\times(a_q\times 10^q+a_{q-1}\times 10^{q-1}+ \cdots +a_{k+2}\times 10^{k+2}+a_{k+1}\times 10^{k+1})-d\times 10^{k+1}$$$. Since we have that $$$a_q$$$ is always no greater than $$$d$$$, we can make sure that $$$9\times(a_q\times 10^q+a_{q-1}\times 10^{q-1}+ \cdots +a_{k+2}\times 10^{k+2}+a_{k+1}\times 10^{k+1})+d\times 10^{k+1}$$$ is always no greater than $$$d \times 10^{q+1}$$$. Therefore, no matter what other position $$$q$$$ we choose to insert $$$d$$$, the result is always no less than inserting at $$$k$$$.

On the other hand, if we insert $$$d$$$ to a less significant position, i.e. between $$$a_{p+1}$$$ and $$$a_p$$$ where $$$p\lt k$$$, then the new number we are going to make is $$$\{a_{L-1}, a_{L-2}, \dots, a_k, \dots, a_{p+1}, d, a_p, \dots, a_0\}$$$ with value $$$N_o = a_{L-1} \times 10^{L}+ a_{L-2} \times 10^{L-1} + \cdots + a_k \times 10^{k+1}+ \cdots +a_{p+1} \times 10^{p+2} + d \times 10^{p+1} + a_p \times 10^p + \cdots +a_0$$$. The difference between this solution and the solution we claimed is $$$N_o-N_g=-d\times 10^{k+1}+9\times(a_k\times 10^k+ \cdots +a_{p+1}\times 10^{p+1})+d\times 10^{p+1}$$$. Since we have that $$$a_k>d$$$, we can make sure that $$$9\times(a_k\times 10^k+ \cdots +a_{p+1}\times 10^{p+1})+d\times 10^{p+1}$$$ is always greater than $$$d\times 10^{k+1}$$$. Therefore, no matter what other position $$$p$$$ we choose to insert $$$d$$$, the result is always greater than inserting at $$$k$$$.

Note that there are some edge cases. For example, all digits in $$$\mathbf{N}$$$ are less than $$$d$$$. In this case, we should append $$$d$$$ to the end of $$$\mathbf{N}$$$. And if $$$d$$$ is $$$0$$$, we will find that the first digit in $$$\mathbf{N}$$$ that is larger than $$$d$$$ is the leading digit. Be careful that we should not put $$$d$$$ before it because the result cannot have leading zeros. In this case, we should put $$$0$$$ right after the leading digit of $$$\mathbf{N}$$$ to get the smallest result.

The time complexity for finding out which $$$d$$$ to insert is $$$O(L)$$$ because we need to add up all digits of $$$\mathbf{N}$$$ to get the remainder of $$$\mathbf{N}$$$ divided by $$$9$$$. Then to find where to insert $$$d$$$, we also need $$$O(L)$$$ time to visit all the digits to find the first digit that is larger than $$$d$$$ (or find out all the digits are no larger than $$$d$$$). Therefore, the total time complexity of this solution is $$$O(L+L)=O(L)$$$.

Test Set 1

Since $$$\mathbf{N}$$$ is small in this test set, we can enumerate all different ways to fill in the question marks recursively, which produces at most $$$2^\mathbf{N}$$$ candidate strings. Then, we check for each string if it contains a palindromic substring of $$$5$$$ or more characters. If it does not, we have found a solution.

Checking for the presence of palindromic substrings can be done naively, by checking every possible substring, which takes $$$O(\mathbf{N}^3)$$$ time ($$$O(\mathbf{N}^2)$$$ substrings times $$$O(\mathbf{N})$$$ to check if a substring is palindromic). It is possible to achieve a lower complexity by searching for the longest palindromic substring in $$$O(\mathbf{N}^2)$$$ or $$$O(\mathbf{N})$$$ time.

The overall time complexity will be between $$$O(2^\mathbf{N} \times \mathbf{N})$$$ and $$$O(2^\mathbf{N} \times \mathbf{N}^3)$$$ but with the given constraints, even the slowest solution should pass.

Test Set 2

If $$$\mathbf{N} \lt 5$$$ the answer is trivially POSSIBLE, so without loss of generality, we will assume $$$\mathbf{N} \ge 5$$$ in the following discussion.

Observation 1: If a string contains a palindromic substring $$$P$$$ of length $$$|P| \gt 6$$$, then it must also contain a palindromic substring of length $$$5$$$ or $$$6$$$. For example, we can take the middle $$$6$$$ characters of $$$P$$$ if $$$|P|$$$ is even, and the middle $$$5$$$ characters otherwise. Consequently, as we fill in the question marks in $$$\mathbf{S}$$$, our only concern is to avoid introducing palindromes of length $$$5$$$ or $$$6$$$.

If at any point in the recursive solution described above, the last $$$5$$$ or $$$6$$$ characters of the prefix generated so far form a palindrome, we can backtrack immediately, thus pruning the search space. If we manage to generate the entire binary string of length $$$\mathbf{N}$$$ without forming a palindrome of length $$$5$$$ or $$$6$$$, the answer is POSSIBLE. Otherwise, we have exhausted the search space with no success, and the answer is IMPOSSIBLE.

This reduces the upper bound to $$$O(2^\mathbf{N})$$$, which is an improvement over the solution for Test Set 1, but it is still prohibitively slow for Test Set 2. It turns out that the complexity is much lower in practice.

Consider again that if we have a valid solution prefix, only its last five characters determine whether it is possible to append a 0 or 1 without introducing a palindrome. That means that all valid strings can be generated by a finite state machine with exactly $$$24$$$ states ($$$32$$$ five-character strings, minus $$$8$$$ palindromes). A transition from abcde to bcdef is possible if and only if neither abcde nor bcdef is a $$$5$$$-character palindrome and abcdef is not a $$$6$$$-character palindrome. All state transitions are shown in the directed graph below:

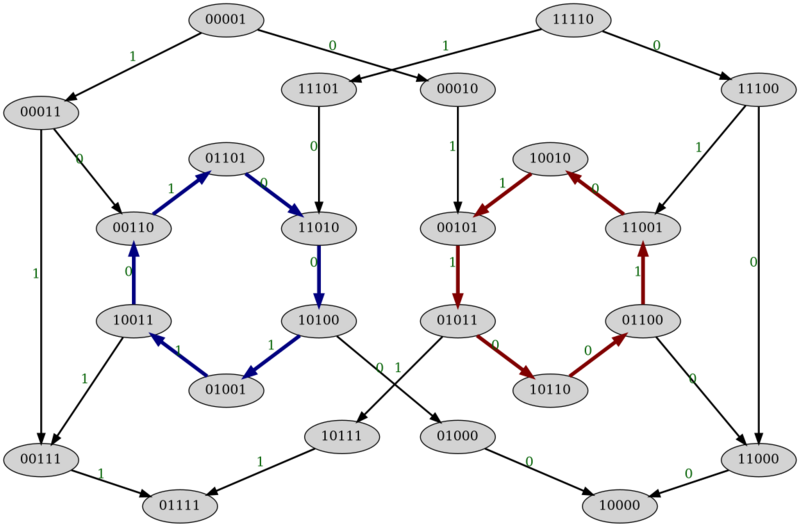
The graph shows, for example, that if the last five characters were 11101 then we can add 0 to obtain 11010, but we cannot add 1, which would create the palindrome 11011. Any valid string can be formed by starting from some vertex (corresponding with the first $$$5$$$ characters of the string) and then following edges of the graph, appending the labels on the edges to the string.

Observation 2: The graph contains only two cycles, which do not overlap and neither is reachable from the other. That means that the only way to form long strings is by repeating the pattern 001101 (going through the left cycle, colored blue) or 110010 (going through the right cycle, colored red). Since we can start and end at any vertex of the graph, there are a few variations possible at both ends of the string, but since the longest path before entering a cycle has length $$$2$$$, and the longest path after exiting from a cycle has length $$$2$$$, all characters in the string except for the first and last two must consist of repetitions of one of the two $$$6$$$-character patterns mentioned before. This gives an upper bound of $$$4 \times 12 \times 4 = 192$$$ palindrome-free strings of any fixed length, though this is an overestimation and it can be shown that the real maximum is only $$$36$$$.

The resursive solution will generate each possible prefix once. Therefore, it takes $$$O(M)$$$ time, where $$$M$$$ is the number of palindrome-free prefixes of the solution. We have shown above that $$$M \le 36\mathbf{N}$$$, which makes the overall runtime $$$O(\mathbf{N})$$$ and allows it to pass without any additional memory.

Dynamic programming solutions

It seems unlikely that contestants would take the time to draw the state graph before attempting to solve the problem, so they might have missed the second observation. Fortunately, it is also possible to solve the problem with only the first observation, by using dynamic programming.

The simplest way to reduce the runtime of the backtracking solution is to add memoization. If the solution is implemented as a function $$$f(p)$$$ where $$$p$$$ is a partial solution string, we can replace this with a function $$$f'(p', i)$$$ where $$$p'$$$ is the $$$5$$$-character suffix of $$$p$$$ and $$$i = |p|$$$ (the length of the prefix, or, equivalently, the position in the input). Observation 1 tells us that these representations are equivalent. We can simply cache the results of $$$f'$$$ for each pair of arguments which requires $$$O(2^5 \times \mathbf{N})$$$ = $$$O(\mathbf{N})$$$ time and space.

A second approach is bottom-up dynamic programming. We process the characters in the input from left to right, while maintaining a set of possible prefixes truncated to the last five characters. To process an input character, we calculate a new set by extending the prefixes from the old set. For example, if the set contains 10100 and the next input character is 1 then we can add 01001 to the next set. If the input character were ? instead, then we could also add 01000. If it becomes empty at any point, the answer is IMPOSSIBLE. If it is nonempty when we reach the end of the input, then the answer is POSSIBLE.

The second approach effectively executes a nondeterministic finite state automaton corresponding with the graph shown above. It is nondeterministic because whenever the input contains a question mark, the transitions labeled with 0 and 1 are both possible, hence the need to track a set of states rather than a single current state only. This approach takes $$$O(2^5 \times \mathbf{N})$$$ = $$$O(\mathbf{N})$$$ time too, but since we only maintain a single set of possible states, the space requirement is reduced to $$$O(2^5) = O(1)$$$.

For simplicity, let us use $$$L_N$$$ to represent the number of digits in an integer $$$N$$$. Note that $$$L_N$$$ is actually equal to $$$\lceil \log_{10}(N + 1) \rceil$$$.

Test Set 1

For the small test set, we can simply enumerate all integers in the range from $$$\mathbf{A}$$$ to $$$\mathbf{B}$$$ and check if each integer is an interesting integer individually. Determining if an integer is interesting or not takes $$$O(L_\mathbf{B})$$$ time (to calculate the sum and product of the digits), where $$$L_\mathbf{B}$$$ is the maximum number of digits in all integers in the range.

The overall time complexity is $$$O((\mathbf{B}-\mathbf{A}) \times L_\mathbf{B})$$$ or just $$$O(\mathbf{B}\log_{10}\mathbf{B})$$$.

Test Set 2

If we have a function $$$CountInterestingIntegers(N)$$$ to get the number of interesting integers between $$$1$$$ and $$$N$$$, then the number of interesting integers between two positive integers $$$\mathbf{A}$$$ and $$$\mathbf{B}$$$ inclusively can be computed by $$$CountInterestingIntegers(\mathbf{B})-CountInterestingIntegers(\mathbf{A}-1)$$$. If $$$N \lt 1$$$, $$$CountInterestingIntegers(N)$$$ is trivially equal to $$$0$$$.

The following are two different methods to compute the value of $$$CountInterestingIntegers(N)$$$.

Method 1

To compute the return value of $$$CountInterestingIntegers(N)$$$, first of all let us define a function $$$f_1(L, P, S)$$$ which returns the number of combinations of arbitrary $$$L$$$ digits $$$d_1,d_2,\dots,d_L$$$ which satisfy the condition that $$$P \times \prod_{i=1}^{L}{d_i}$$$ is divisible by $$$S + \sum_{i=1}^{L}{d_i}$$$, which can be written as $$$(P \times \prod_{i=1}^{L}{d_i}) \% (S + \sum_{i=1}^{L}{d_i}) = 0$$$.

Based on the definition above, for $$$L=0$$$, the return value of $$$f_1(L, P, S)$$$ is $$$1$$$ if $$$P \% S = 0$$$, and $$$0$$$ otherwise. For $$$L \gt 0$$$, the return value of $$$f_1(L, P, S)$$$ is $$$\sum_{digit=0}^{9}{f_1(L-1, P\times digit, S + digit)}$$$. In the implementation, we can use top-down dynamic programming to memoize the return values of $$$f_1$$$ with different parameter sets in a hash table to speed up the function calls.

Afterward, we can compute the value of $$$CountInterestingIntegers(N)$$$ by recursively visiting each digit of $$$N$$$ from left (0, the most significant digit) to right ($$$L_N - 1$$$, the least significant digit) to construct integers smaller than $$$N$$$ and check the number of interesting integers with function $$$f_1$$$. The following is the pseudo code for $$$CountInterestingIntegers$$$:

def CountInterestingIntegers(N):
  if N == 0:
    return 0
  count = 0
  for L in (1 to (CountDigits(N) - 1)):
    count += CountInterestingIntegersWithNumberOfDigits(L)

  count += CountInterestingIntegersWithPrefixOfN(N, P=1, S=0, digit_index=0, is_first_digit=True)
  return count

def CountInterestingIntegersWithNumberOfDigits(L):
  count = 0
  for digit in (1 to 9):
    count += f1(L - 1, P=digit, S=digit)
  return count

def CountInterestingIntegersWithPrefixOfN(N, P, S, digit_index, is_first_digit):
  if digit_index == CountDigits(N):
    return 1 if S > 0 and P % S == 0 else 0

  if is_first_digit:
    digit_start = 1
  else:
    digit_start = 0

  count = 0
  for digit in (digit_start to (GetIthDigit(N, digit_index) - 1)):
    count += f1(CountDigits(N) - digit_index - 1, P * digit, S + digit)

  count += CountInterestingIntegersWithPrefixOfN(N,
                                                 P * GetIthDigit(N, digit_index),
                                                 S + GetIthDigit(N, digit_index),
                                                 digit_index + 1, is_first_digit=False)
  return count

Let $$$M$$$ be the number of digits in the maximum number in all possible ranges from $$$\mathbf{A}$$$ to $$$\mathbf{B}$$$. The number of possible parameter sets of $$$f_1(L, P, S)$$$ is bounded by $$$M \times (\frac{(M+9-1)!}{(9-1)!M!} + 1) \times (9 \times M)$$$, where the number of possible products is bounded by the combinations of choosing $$$M$$$ digits from $$$\{1,2,3,\dots,9\}$$$ without repetitions, plus 1 (the zero product). Besides, computing the return value of $$$f_1(L, P, S)$$$ takes $$$O(1)$$$ time with memoization. Therefore, the overall time complexity of $$$f_1(L, P, S)$$$ is $$$O(M \times (\frac{(M+9-1)!}{(9-1)!M!} + 1) \times (9 \times M))$$$. Since $$$ \mathbf{A}, \mathbf{B} \le 10^{12}$$$ from the problem statement, we can derive that $$$M=13$$$ and the number of parameter sets is at most $$$13 \times 203,491 \times (9 \times 13)$$$, which is equal to $$$309,509,811$$$.

A tighter estimate for the number of possible sets of $$$f_1(L, P, S)$$$ is $$$O(\sum_{L=1}^{M}{(\frac{(L+9-1)!}{(9-1)!L!} + 1) \times (9 \times L)})$$$, which is bounded by $$$52,379,145$$$ when $$$M=13$$$. In fact, only $$$188,701$$$ entries are kept in the memoization of $$$f_1$$$ after solving all the test cases in test set 2, which is much smaller than the estimate.

The function $$$CountInterestingIntegers(N)$$$ takes $$$O(M)$$$ to get the number of interesting integers from $$$0$$$ to $$$N$$$ with the memoization of $$$f_1$$$. Therefore, the overall time complexity for method 1 is $$$O(M)$$$, where $$$M$$$ is equal to $$$\lceil \log_{10}(\mathbf{B} + 1) \rceil$$$.

Notice that the memoization for the return values of $$$f_1(L, P, S)$$$ can be reused in all the test cases. Clearing and rebuilding the memoization for every test case may make the implementation exceed time limit since there are 100 test cases in test set 2.

Optimization for Method 1 with Prime Factorization

Since the value of parameter $$$P$$$ passed to $$$f_1(L, P, S)$$$ is always a product of digits, it can be written as $$$P = 2^w \times 3^x \times 5^y \times 7^z$$$, where $$$2, 3, 5, 7$$$ are what we call "interesting prime factors" and $$$w, x, y, z$$$ are powers of these prime factors. Moreover, the maximum possible value of parameter $$$S$$$ is $$$9M$$$. From these two observations, we can find out that if $$$2^w \gt 9M$$$, then $$$P \% S = 0$$$ if and only if $$$(P/2) \% S = 0$$$ for any $$$S \le 9M$$$. This observation applies to other interesting prime factors as well.

Based on the observation aforementioned, we can further improve the performance by reducing the number of possible parameter sets of $$$f_1(L, P, S)$$$ by the idea of capping the power of interesting prime factors. Let us define a helper function $$$CapInterestingPrimeFactors(P)$$$ which does the following things:

1. Compute the power of interesting prime factors $$$w,x,y,z$$$ of input $$$P = 2^w \times 3^x \times 5^y \times 7^z$$$.

2. For each interesting prime factor $$$p$$$, define the power of it as $$$v$$$ and compute the new power as the maximum value of $$$v'$$$ which satisfies $$$p^{v'} \le 9M$$$ and $$$v' \le v$$$.

3. Construct the new product $$$P' = 2^{w'} \times 3^{x'} \times 5^{y'} \times 7^{z'}$$$ and return it.

Afterwards, we can replace all the function calls $$$f_1(L, P, S)$$$ with $$$f_1(L, CapInterestingPrimeFactors(P), S)$$$. Since the maximum possible value of $$$S = 9 \times 13 = 117$$$ in test set 2 (this is just an upper bound based on the definition above), the maximum value of $$$P'$$$ after capping is $$$2^{6} \times 3^{4} \times 5^{2} \times 7^{2}$$$, and the total number of possible values of $$$CapInterestingPrimeFactors(P)$$$ is $$$7 \times 5 \times 3 \times 3 = 315$$$. Therefore, the number of parameter sets of the improved $$$f_1(L, P', S)$$$ is at most $$$13 \times 315 \times (9\times13) = 479,115$$$ which is a huge improvement over the pre-optimized method 1. In fact, only 56,853 entries are kept in the memoization of $$$f_1$$$ after solving all the test cases in test set 2.

Method 2

Method 2 is similar to method 1 but we set a fixed target digit sum when computing the number of interesting integers, then add up the number of interesting integers with all possible digit sums.

Let us define another function $$$f_2(L, P, S, S_{target})$$$ which returns the number of combinations of arbitrary $$$L$$$ digits $$$d_1,d_2,\dots,d_L$$$ that satisfy the conditions:

• $$$S + \sum_{i=1}^{L}{d_i} = S_{target}$$$

• $$$P \times \prod_{i=1}^{L}{d_i}$$$ is divisible by $$$S_{target}$$$ ($$$(P \times \prod_{i=1}^{L}{d_i}) \% S_{target} = 0$$$)

Notice that $$$f_2(L, P, S, S_{target}) = f_2(L, P \% S_{target}, S, S_{target})$$$. For $$$L=0$$$, the return value is $$$1$$$ if $$$S=S_{target}$$$ and $$$P\%S_{target}=0$$$, and $$$0$$$ otherwise. For $$$L\gt 0$$$, the return value of $$$f_2(L, P, S, S_{target})$$$ is equal to $$$\sum_{digit=0}^{9}{f_2(L-1, (P\times digit) \% S_{target}, S + digit, S_{target})}$$$.

In the implementation, we can pre-compute return values of $$$f_2$$$ with all possible parameter sets and store the values in a 4-dimensional array or hash map. Let $$$M$$$ be the number of digits in the maximum number in all possible ranges from $$$\mathbf{A}$$$ to $$$\mathbf{B}$$$, the possible digits sum ranges from $$$1$$$ to $$$9 \times M$$$. Therefore, the number of parameter combinations is bounded by $$$M(9M)^3$$$, and it takes $$$O(M\times(9M)^3)$$$ time and space to build the memoization with top-down dynamic programming. Since $$$ \mathbf{A}, \mathbf{B} \le 10^{12}$$$ from the problem statement, we can derive that $$$M=13$$$ and the number of parameter sets is at most $$$13 \times (9 \times 13)^3$$$, which is equal to $$$20,820,969$$$. Notice that this memoization can be built only once and reused in all test cases. Clearing and rebuilding the memoization for every test case may make the implementation time out since there are 100 test cases in test set 2.

Afterward, we can compute the value of $$$CountInterestingIntegers(N)$$$ by enumerating all possible values of $$$S_{target}$$$ and recursively visiting each digit of $$$N$$$ from left (0, the most significant digit) to right ($$$L_N - 1$$$, the least significant digit) to construct integers smaller than $$$N$$$ and check the number of interesting integers with function $$$f_2$$$. The following is the pseudo code for $$$CountInterestingIntegers$$$:

def CountInterestingIntegers(N):
  if N == 0:
    return 0

  count = 0
  for S_target in (1 to (9 * CountDigits(N))):
    for L in (1 to (CountDigits(N) - 1)):
      count += CountInterestingIntegersWithNumberOfDigits(S_target, L)

    count += CountInterestingIntegersWithPrefixOfN(S_target, N, P=1, S=0,
                                                   digit_index=0, is_first_digit=True)
  return count

def CountInterestingIntegersWithNumberOfDigits(S_target, L):
  count = 0
  for digit in (1 to 9):
    count += f2(L - 1, P=(digit % S_target), S=digit, S_target)
  return count

def CountInterestingIntegersWithPrefixOfN(S_target, N, P, S, digit_index, is_first_digit):
  if digit_index == CountDigits(N):
    return 1 if P % S == 0 and S == S_target else 0

  if is_first_digit:
    digit_start = 1
  else:
    digit_start = 0

  count = 0
  for digit in (digit_start to (GetIthDigit(N, digit_index) - 1)):
    count += f2(CountDigits(N) - digit_index - 1, (P * digit) % S_target, S + digit, S_target)

  count += CountInterestingIntegersWithPrefixOfN(S_target, N,
                                                 (P * GetIthDigit(N, digit_index)) % S_target,
                                                 S + GetIthDigit(N, digit_index),
                                                 digit_index + 1, is_first_digit=False)
  return count

The overall time complexity is $$$O(M\times(9M)^3)$$$ to pre-compute the memoization of $$$f_2$$$, and $$$O(9M \times M)$$$ to get the number of interesting integers between $$$\mathbf{A}$$$ and $$$\mathbf{B}$$$ with memoization. Although method 2 adds one more parameter that is seemingly redundant, it has better and clearer time and space complexity estimates for building the memoization considering that the product can be a seemingly arbitrary number, while product modulo sum is bounded by a much smaller value. However, after solving all the test cases in test set 2, $$$2,406,887$$$ entries are kept in the memoization of $$$f_2$$$, which takes more time and space than method 1. We may apply some optimizations to $$$f_2$$$ to further reduce the memoization size and make it more performant, like returning $$$0$$$ early when $$$S_{target} \gt 9 \times L$$$.