Google Kick Start Archive — Round G 2021 problems
Overview
Thank you for participating in Kick Start 2021 Round G!
Cast
Dogs and Cats: Written by Sumedha Agarwal and prepared by Chu-ling Ko.
Staying Hydrated: Written by Deepika Naryani and prepared by Gagan Kumar.
Banana Bunches: Written by Claire Yang and prepared by Anson Ho.
Simple Polygon: Written by Pablo Heiber and prepared by Mahmoud Ezzat.
Solutions, other problem preparation, reviews and contest monitoring by Abhishek Singh, Akul Siddalingaswamy, Alan Lou, Anson Ho, Anurag Singh, Bartosz Kostka, Bohdan Pryshchenko, Chu-ling Ko, Chun-nien Chan, Claire Yang, Cristhian Bonilha, Dee Guo, Deeksha Kaurav, Deep Chowdhury, Deepak Gour, Deepika Naryani, Diksha Saxena, Gagan Kumar, Ishank Bhardwaj, Ishita Mundhra, Jared Gillespie, Kashish Bansal, Krists Boitmanis, Lizzie Sapiro Santor, Lucas Maciel, Mahmoud Ezzat, Maneeshita Sharma, Michał Łowicki, Mo Luo, Pablo Heiber, Phil Sun, Pranjal Jain, Rahul Goswami, Rathin Bhargava, Rishabh Agarwal, Ruoyu Zhang, Samiksha Gupta, Sangeeta Mishra, Sara Biavaschi, Sarah Young, Sasha Fedorova, Sharath Holla, Shweta Karwa, Sumedha Agarwal, Swapnil Gupta, Swapnil Mahajan, Teja Vardhan Reddy Dasannagari, Umang Goel, Vasyl Franchuk, Vijay Krishan Pandey.
Analysis authors:
- Dogs and Cats: Vijay Krishan Pandey
- Staying Hydrated: Krists Boitmanis
- Banana Bunches: Swapnil Gupta
- Simple Polygon: Krists Boitmanis
A. Dogs and Cats
Problem
You work for an animal shelter and you are responsible for feeding the animals. You already prepared $$$\mathbf{D}$$$ portions of dog food and $$$\mathbf{C}$$$ portions of cat food.
There are a total of $$$\mathbf{N}$$$ animals waiting in a line, some of which are dogs and others are cats. It might be possible
that all the animals in the line are dogs or all the animals are cats.
A string $$$\mathbf{S}$$$ of $$$\mathbf{N}$$$ characters C and D represents the order of cats and dogs in the line.
The $$$i$$$-th character is equal to C if the $$$i$$$-th animal in the line is a cat.
Similarly, the $$$i$$$-th character is equal to D if the $$$i$$$-th animal in the line is a dog.
The animals are fed in the order they stay in the line. Each dog eats exactly $$$1$$$ portion of dog food and similarly each cat eats exactly $$$1$$$ portion of cat food. Moreover, you have extra portions of cat food. Every time a dog eats food, you bring $$$\mathbf{M}$$$ extra portions of cat food for cats.
Animals have to be fed in the order they wait in line and an animal can only eat if the animal before it has already eaten. That means that if you run out of dog (or cat) food portions and a dog (or a cat) is about to get fed, the line will not move, as all the animals will wait patiently.
You need to determine if in this scenario all the dogs in the line will be fed. Note that this means that some cats might remain in the line, but worry not, you will eventually feed them later!
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow.
The first line of each test case contains four integers $$$\mathbf{N}$$$, $$$\mathbf{D}$$$, $$$\mathbf{C}$$$, and $$$\mathbf{M}$$$: the number of animals, the initial number of dog food portions, the initial number of cat food portions, and the additional portions of cat food that we add after a dog eats a portion of dog food, respectively.
The next line contains a string $$$\mathbf{S}$$$ of length $$$\mathbf{N}$$$ representing the arrangement of animals.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$,
where $$$x$$$ is the test case number (starting from $$$1$$$) and $$$y$$$ is YES
if all the dogs will be fed and NO otherwise.
Limits
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$1 \le \mathbf{N} \le 10^4$$$.
$$$0 \le \mathbf{D}, \mathbf{C} \le 10^6$$$.
$$$\mathbf{S}$$$ consists of only characters C and D.
Test Set 1
Time limit: 20 seconds.
$$$\mathbf{M} = 0$$$
Test Set 2
Time limit: 40 seconds.
$$$0 \le \mathbf{M} \le 10^6$$$.
Sample
Note: there are additional samples that are not run on submissions down below.3 6 10 4 0 CCDCDD 4 1 2 0 CCCC 4 2 1 0 DCCD
Case #1: YES Case #2: YES Case #3: NO
In Sample Case #1, there are $$$10$$$ portions of dog food and $$$4$$$ portions of cat food.
- The first two animals are cats, so after they eat, $$$2$$$ portions of cat food remain.
- Then a dog eats one portion of dog food. Now, there are $$$9$$$ portions of dog food left.
- Next, a cat eats a portion of cat food, reducing the number of portions of cat food to $$$1$$$.
- The last two animals are dogs and they each eat one portion of dog food.
In Sample Case #2, there are no dogs. Hence, all (zero) dogs will be able to eat trivially.
In Sample Case #3, the cat before the second dog will not be able to eat because there will not be enough portions of cat food. Hence, the second dog will also not eat.
Additional Sample - Test Set 2
The following additional sample fits the limits of Test Set 2. It will not be run against your submitted solutions.2 12 4 2 2 CDCCCDCCDCDC 8 2 1 3 DCCCCCDC
Case #1: YES Case #2: NO
In Sample Case #1, $$$2$$$ portions of cat food appear whenever a dog eats a portion of dog food.
- After the first cat eats, there is $$$1$$$ portion of cat food left.
- Then a dog eats, leaving $$$3$$$ portions of dog food and $$$3$$$ portions of cat food.
- After the next $$$3$$$ cats eat, there are $$$3$$$ portions of dog food and $$$0$$$ portions of cat food remaining.
- Then a dog eats, leaving $$$2$$$ portions of dog food and $$$2$$$ portions of cat food.
- After the next $$$2$$$ cats eat food, there are $$$2$$$ portions of dog food and $$$0$$$ portions of cat food left.
- Now a dog eats, leaving $$$1$$$ portion of dog food and $$$2$$$ portions of cat food.
- Next a cat eats, leaving $$$1$$$ portion of dog food and $$$1$$$ portion of cat food.
- The last dog eats the remaining portion of dog food.
In Sample Case #2, the cat before the second dog will not be able to eat because there will not be enough portions of cat food.
B. Staying Hydrated
Problem
With online classes in full swing, it is important for Grace to take breaks and keep herself hydrated at all times. She has decided to place a water bottle in her room in the most convenient place. This means that the position of this water bottle should be close to all the places in the room where she generally hangs out like the study desk, bed and coffee table among other places.
The room is represented in the form of a coordinate plane. The number of steps Grace needs to go from Point A to Point B is equal to the Manhattan distance between the 2 points. This means, Grace can only walk parallel to the axes of the coordinate plane and with each step, she can move one unit in either of the four directions.
Can you help her find a position in the room to keep the bottle, such that the sum of steps from the bottle to all her favourite furniture pieces will be minimum?
Notes:
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow.
The first line of each test case contains an integer $$$\mathbf{K}$$$ which represents the number of objects in
Grace's room.
$$$\mathbf{K}$$$ lines follow, each of them describing one object. The $$$i$$$-th line contains four integers,
$$$\mathbf{x_{i,1}}$$$, $$$\mathbf{y_{i,1}}$$$, $$$\mathbf{x_{i,2}}$$$, $$$\mathbf{y_{i,2}}$$$, where ($$$\mathbf{x_{i,1}}$$$, $$$\mathbf{y_{i,1}}$$$) represents coordinates of
the bottom left corner and ($$$\mathbf{x_{i,2}}$$$, $$$\mathbf{y_{i,2}}$$$) represents coordinates of the top right corner of
the $$$i$$$-th rectangular object.
Output
For each test case, output one line containing Case #$$$i$$$: $$$x$$$ $$$y$$$,
where $$$i$$$ is the test case number (starting from 1) and $$$x$$$ and $$$y$$$ are coordinates of
the water bottle such that the sum of steps from these coordinates to all the furniture
pieces will be minimum.
Note, the bottle can lie on the floor or on top of any furniture but should be placed on integer
coordinates only.
If multiple solutions exist, output the one with minimum x coordinate, if multiple solutions have
the same x coordinate output the one with minimum y coordinate.
Limits
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$\mathbf{x_{i,1}} \lt \mathbf{x_{i,2}}$$$, for all $$$i$$$.
$$$\mathbf{y_{i,1}} \lt \mathbf{y_{i,2}}$$$, for all $$$i$$$.
Test Set 1
Time limit: 40 seconds.
$$$1 \le \mathbf{K} \le 20 $$$.
$$$-100 \le \mathbf{x_{i,1}},\mathbf{x_{i,2}},\mathbf{y_{i,1}},\mathbf{y_{i,2}} \le 100$$$, for all $$$i$$$.
Test Set 2
Time limit: 90 seconds.
$$$1 \le \mathbf{K} \le 10^5$$$
$$$-10^9 \le \mathbf{x_{i,1}},\mathbf{x_{i,2}},\mathbf{y_{i,1}},\mathbf{y_{i,2}} \le 10^9$$$, for all $$$i$$$.
Sample
2 3 0 0 1 1 2 3 4 6 0 3 5 9 1 0 0 1 1
Case #1: 1 3 Case #2: 0 0
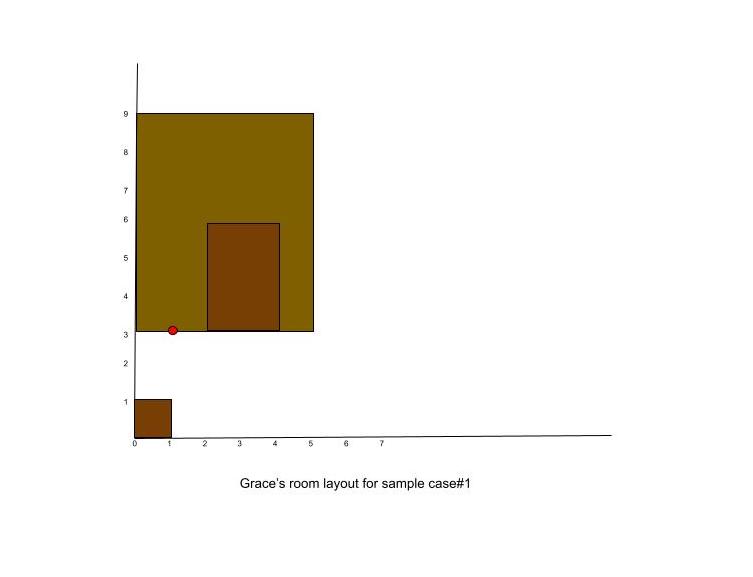
In Sample Case #1, Grace can place the bottle at coordinates ($$$1$$$, $$$3$$$). It is at a distance of $$$2$$$ steps from first object, $$$1$$$ step from second and $$$0$$$ steps from the third one which gives us $$$3$$$ as the minimum possible sum of steps from a point.
In Sample Case #2, the water bottle can lie anywhere on the object itself but coordinates ($$$0$$$, $$$0$$$) correspond to the minimum x and y coordinates.
C. Banana Bunches
Problem
Barbara goes to Alan's banana farm, where the $$$\mathbf{N}$$$ banana trees are organized in one long line
represented by an array $$$\mathbf{B}$$$. The tree at position $$$i$$$ has $$$\mathbf{B_i}$$$ banana bunches. Each tree
has the same cost. Once Barbara buys a tree, she gets all the banana bunches on that tree.
Alan has a special rule: because he does not want too many gaps in his line, he allows Barbara
to buy at most $$$2$$$ contiguous sections of his banana tree line.
Barbara wants to buy some number of trees such that the total number of banana bunches on these purchased trees equals the capacity $$$\mathbf{K}$$$ of her basket. She wants to do this while spending as little money as possible. How many trees should she buy?
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow.
Each test case begins with a line containing two integers integer $$$\mathbf{N}$$$, the number of trees on
Alan's farm, and $$$\mathbf{K}$$$, the capacity of Barbara's basket.
The next line contains $$$\mathbf{N}$$$ non-negative integers $$$\mathbf{B_1}, \mathbf{B_2},\dots, \mathbf{B_N}$$$ representing array $$$\mathbf{B}$$$, where
the $$$i$$$-th integer represents the number of banana bunches on the $$$i$$$-th tree on Alan's
farm.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$,
where $$$x$$$ is the test case number (starting from $$$1$$$) and $$$y$$$ is the minimum number
of trees Barbara must purchase to obtain $$$\mathbf{K}$$$ banana bunches using at most $$$2$$$ contiguous
sections of the farm, or -1 if it is impossible to do so.
Limits
Time limit: 20 seconds.
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$0 \le \mathbf{B_{i}} \le \mathbf{K}$$$, for each $$$i$$$ from $$$1$$$ to $$$\mathbf{N}$$$.
Test Set 1
$$$1 \le \mathbf{K} \le 10^4$$$.
$$$1 \le \mathbf{N} \le 50$$$.
Test Set 2
$$$1 \le \mathbf{K} \le 10^4$$$.
$$$1 \le \mathbf{N} \le 500$$$.
Test Set 3
$$$1 \le \mathbf{K} \le 10^6$$$.
For at most 25 cases:
$$$1 \le \mathbf{N} \le 5000$$$.
For the remaining cases:
$$$1 \le \mathbf{N} \le 500$$$.
Sample
4 6 8 1 2 3 1 2 3 4 10 6 7 5 2 6 8 3 1 2 1 3 1 4 6 3 1 2 0
Case #1: 3 Case #2: -1 Case #3: 4 Case #4: 3
In Sample Case #1, the first section can contain the trees at indices $$$2$$$ and $$$3$$$, and the second section can contain the tree at index $$$6$$$.
In Sample Case #2, it is impossible to achieve a sum of $$$10$$$ with $$$2$$$ contiguous sections.
In Sample Case #3, the first section can contain the trees at indices $$$\{1, 2\}$$$, and the second section can contain the trees at indices $$$\{5, 6\}$$$. We cannot take the $$$2 + 3 + 3$$$ combo (trees at indices $$$\{1, 3, 5\}$$$) since that would be $$$3$$$ contiguous sections.
In Sample Case #4, the only section contains the trees at indices $$$\{1, 2, 3\}$$$.
D. Simple Polygon
Problem
You are given two integers, the number of vertices $$$\mathbf{N}$$$ and area $$$\mathbf{A}$$$. You need to construct a simple polygon of $$$\mathbf{N}$$$ vertices such that the area of the polygon is exactly $$$\frac{\mathbf{A}}{2}$$$, and all the vertices have non-negative integer coordinates with value up to $$$10^9$$$.
A simple polygon is one that:
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ lines follow. The first line of each test case contains two integers, $$$\mathbf{N}$$$ denoting the number of vertices and $$$\mathbf{A}$$$, denoting double the required area of the polygon.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$,
where $$$x$$$ is the test case number (starting from 1) and $$$y$$$ is
IMPOSSIBLE if it is not possible to construct a polygon with the given requirements
and POSSIBLE otherwise.
If you output POSSIBLE,
output $$$\mathbf{N}$$$ more lines with $$$2$$$ integers each.
The $$$i$$$-th line should contain two
integers $$$X_{i}$$$ and $$$Y_{i}$$$ which denote the coordinates of the $$$i$$$-th vertex. For each
$$$i$$$, the coordinates should satisfy the $$$0 \le X_{i}, Y_{i} \le 10^9$$$ constraints.
Vertices of the polygon should be listed in consecutive order ( $$$vertex_{i}$$$ should be adjacent
to $$$vertex_{i-1}$$$ and $$$vertex_{i+1}$$$ in the polygon).
If there are multiple possible solutions, you can output any of them.
Limits
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$1 \le \mathbf{A} \le 10^9$$$.
Test Set 1
Time limit: 20 seconds.
$$$3 \le \mathbf{N} \le 5$$$.
Test Set 2
Time limit: 40 seconds.
$$$3 \le \mathbf{N} \le 1000$$$.
Sample
2 4 36 5 2
Case #1: POSSIBLE 2 5 6 5 8 2 0 2 Case #2: IMPOSSIBLE
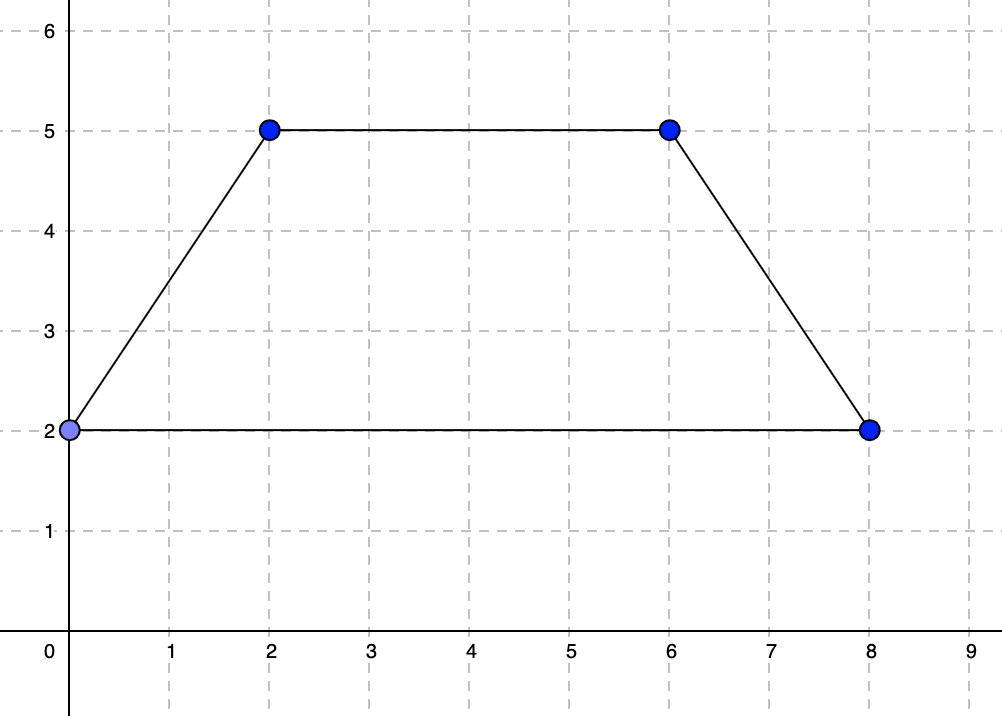
In Sample Case #1, we can output the above quadrilateral with coordinates $$$(2, 5)$$$, $$$(6, 5)$$$, $$$(0, 2)$$$ and $$$(8, 2)$$$. The area of this quadrilateral is equal to $$$18$$$.
In Sample Case #2, there is no way to construct a polygon with $$$5$$$ vertices and area equal to $$$1$$$.
Analysis — A. Dogs and Cats
We need to determine if all the dogs will be able to eat food given the condition that an animal can only eat if the animal before it has already eaten. We do not worry if some cats are hungry as long as all the dogs are able to eat. Let us assume that the last (or rightmost) dog is at position $$$p$$$. We do not need to worry about the cats in positions $$$[p + 1, N]$$$. Since an animal can only eat food if the animal before it has already eaten, we need to make sure that all cats and dogs in positions $$$[1, p]$$$ are able to eat food.
Test Set 1
We are given $$$\mathbf{M}$$$ $$$= 0$$$. This means whenever a dog eats food, no cat foods magically appear. If
$$$\mathbf{S}$$$ contains all $$$0$$$ i.e., no dog is present, the answer is YES. Otherwise, we find the position
of the last (or rightmost) dog, $$$p$$$. Let the total number of dogs i.e., the number of $$$1$$$ in $$$\mathbf{S}$$$ be $$$X$$$ and the number of cats
before the rightmost dog i.e., the number of $$$0$$$ in $$$[1, p - 1]$$$ be $$$Y$$$. The answer is YES
if $$$\mathbf{D} \ge X$$$ and $$$\mathbf{C} \ge Y$$$ and NO otherwise.
Complexity : $$$O(\mathbf{N})$$$ per test case
Test Set 2
We are given $$$\mathbf{M} \ge 0$$$. This means whenever a dog eats food, $$$\mathbf{M}$$$ cat food portions are added.
We iterate over positions $$$[1,N]$$$ and whenever we see a cat we feed it with the cat food i.e.,
subtract $$$1$$$ from $$$\mathbf{C}$$$ and whenever a dog appears we feed it with the dog food,
i.e., subtract $$$1$$$ from $$$\mathbf{D}$$$. We need to ensure that the dog can only
eat if the animal before it has already eaten, and to do so, we first make sure that $$$\mathbf{D} \ge 1$$$,
as $$$1$$$ food item is needed to feed this dog and $$$\mathbf{C} \ge 0$$$. If this is not true, our
answer is NO. Otherwise we subtract $$$1$$$ from $$$\mathbf{D}$$$ and add $$$\mathbf{M}$$$ to $$$\mathbf{C}$$$.
If the above condition is satisfied for all the dogs, our answer is YES. Note that this
algorithm will also work for Test Set $$$1$$$ but not vice versa.
Sample Code(C++)
bool have_dogs_eaten(string S, int N, int D, long long C, int M) {
for(int i = 0; i < N; i++) {
if (S[i] == '1') {
if(D <= 0 || C < 0) {
return false;
}
D--;
C += M;
} else {
C--;
}
}
return true;
}
C is long long since maximum possible value does not fit in 32-bit data type.
Complexity : $$$O(\mathbf{N})$$$ per test case
Analysis — B. Staying Hydrated
The Manhattan distance between a point $$$P=(x,y)$$$ and an axis-parallel rectangle $$$R$$$ with the lower-left corner $$$(x_1,y_1)$$$ and the upper-right corner $$$(x_2,y_2)$$$ is $$$d(P,R)=\max(x_1 - x, x - x_2, 0) + \max(y_1 - y, y - y_2, 0)$$$. Intuitively, the first term represents the minimal horizontal movement from $$$P$$$ to the nearest point inside the $$$x$$$-interval $$$[x_1,x_2]$$$, which could be $$$0$$$ if $$$P$$$ itself is in that interval. Similarly, the second term represents the minimal vertical movement from $$$P$$$ to the nearest point inside the $$$y$$$-interval $$$[y_1,y_2]$$$.
Test Set 1
In this test set, the furnished area of the room is so small that we can afford testing every point $$$P=(x,y)$$$ in the range $$$-100 \le x,y \le 100$$$ and select the point with the smallest total distance to all rectangular objects. The time complexity of such a brute-force algorithm is $$$O(\mathbf{K}WH)$$$, where $$$\mathbf{K}$$$ is the number of input objects and $$$W$$$ and $$$H$$$ is the width and the height of the smallest axis-parallel rectangle covering all input rectangles. Note that it is not necessary to test any points outside this covering rectangle as moving from such a point towards the covering rectangle would reduce the distance to all input rectangular objects. The time complexity can be further improved to $$$O(\mathbf{K}(W + H))$$$ if we realize that the optimal $$$x$$$- and $$$y$$$-coordinates are in fact independent and can be calculated separately.
Test Set 2
In this test set, the furnished area of the room may be huge, therefore, even the improved version of the brute-force algorithm would be too slow. However, with a little bit of sorting, we can find the optimal location of the bottle without ever computing any distances.
Let us consider finding the optimal $$$x$$$-coordinate of the bottle (the optimal $$$y$$$-coordinate can be found in the same way). Imagine that we are seeking the optimal location by sweeping the coordinate plane from left to right. Suppose we are currently at the position $$$x$$$ and let $$$a(x)$$$ be the number of rectangles that are strictly ahead of $$$x$$$, i.e. $$$x \lt x_1$$$, where $$$x_1$$$ is the left coordinate of the rectangle. Simlarly, let $$$b(x)$$$ be the number of rectangles that are behind $$$x$$$ in the non-strict sense, namely, $$$ x_2 \le x$$$. Now, if $$$a(x) \gt b(x)$$$, then $$$x$$$ is not the optimal location as moving one step to the right would reduce the total horizontal distance to the rectangles by $$$a(x)-b(x) \gt 0$$$.
What happens to the value of $$$a(x)-b(x)$$$ as we sweep the plane from left to right? For a sufficiently small $$$x$$$, which is strictly to the left from all rectangles, $$$a(x)=\mathbf{K}$$$ and $$$b(x)=0$$$, and therefore, $$$a(x)-b(x) = \mathbf{K} \gt 0$$$. Conversely, for a sufficiently large $$$x$$$, it is the other way around and $$$a(x)-b(x) = -\mathbf{K} \lt 0$$$. And since $$$a(x)$$$ is a decreasing function while $$$b(x)$$$ is an increasing function, the difference $$$a(x)-b(x)$$$ is also a decreasing function. What does it mean for our plane sweeping approach? As long as $$$a(x)-b(x) \gt 0$$$, we should keep moving to the right as, by doing so, we are reducing the total distance to the rectangles. But as soon as $$$a(x)-b(x) \le 0$$$, we have found the optimal $$$x$$$-coordinate, since further reduction of the total distance is not possible.
In summary, we have reduced the task of calculating the optimal Manhattan distance to finding the smallest $$$x$$$ with $$$a(x)-b(x) \le 0$$$. This can be done by iterating through the left and right coordinates of rectangles in sorted non-decreasing order and maintaining the values of functions $$$a(x)$$$ and $$$b(x)$$$. The time complexity of this algorithm is dominated by the sorting, and is therefore $$$O(\mathbf{K} \log \mathbf{K})$$$.
Left as an exercise to the reader: This problem can also be solved in $$$O(\mathbf{K})$$$ by using linear-time selection algorithms. Though both our test sets should pass with the above $$$O(\mathbf{K} \log \mathbf{K})$$$ approach.
Analysis — C. Banana Bunches
Formally the problem can be written as: given an array of size $$$\mathbf{N}$$$, select at most two non-overlapping subarrays, such that, sum of all the selected elements is equal to $$$\mathbf{K}$$$. We need to minimise the sum of lengths of these two subarrays. We can calculate the prefix sum of the given array in $$$O(\mathbf{N})$$$. $$$Pre_{i}$$$ denotes the sum of all the elements from $$$1$$$ to $$$i$$$. The sum of elements in a particular $$$subarray(i, j)$$$ is given by $$$Pre_{j} - Pre_{i-1}$$$ and can be calculated in $$$O(1)$$$ time.
One special case is when there is an element equal to $$$\mathbf{K}$$$ in the given array. In this case, we can return $$$1$$$ as the answer and can be done in a $$$O(\mathbf{N})$$$ traversal. For all the other cases, we can get the answer by selecting two non-overlapping subarrays.
Test set 1
For this test set, we can consider all possible pair of subarrays as constraints on $$$\mathbf{N}$$$ are small. The total number of pair of subarrays are $$$O(\mathbf{N}^{4})$$$. For each pair of non-overlapping subarrays, one can check whether the sum of elements in these subarrays is equal to $$$\mathbf{K}$$$. Formally, consider all $$$(i, j, x, y)$$$ such that sum of $$$subarray(i, j)$$$ and $$$subarray(x, y)$$$ is equal to $$$\mathbf{K}$$$ and $$$i \le j \lt x \le y$$$. Among all such pairs of subarrays, the optimal answer is the pair with the minimum sum of length of the subarrays. Formally, we need to minimise $$$j - i + 1 + y - x + 1$$$ over all such pairs. For each pair, one can calculate the sum and length of these subarrays in $$$O(1)$$$. Hence, the overall complexity of the solution is $$$O(\mathbf{N}^{4})$$$.
Test set 2
For this test set, we cannot consider all possible pair of subarrays as this solution would time out with the given constraints. We can iterate on all possible $$$(i, j, x)$$$ and find an optimal index $$$y$$$ such that sum of $$$subarray(i, j)$$$ and $$$subarray(x, y)$$$ is equal to $$$\mathbf{K}$$$ and $$$i \le j \lt x \le y$$$. For a particular $$$(i, j, x)$$$ we need to find smallest index $$$y$$$ such that $$$Pre_{j}-Pre_{i-1} + Pre_{y} - Pre{x-1} = \mathbf{K}$$$. This can be done by performing a binary search on indexes from $$$x$$$ to $$$N$$$. If there is no such index $$$y$$$, we can ignore this triplet. Among all such possible $$$(i, j, x, y)$$$ quadruples, we need to minimise $$$j - i + 1 + y - x + 1$$$. We are able to find an optimal index $$$l$$$ in $$$O(\log \mathbf{N})$$$ time complexity for a particular triplet $$$(i, j, x)$$$. There are $$$O(\mathbf{N}^{3})$$$ such triplets. Hence, the overall complexity of the solution is $$$O(\mathbf{N}^{3} \log \mathbf{N})$$$.
We can further reduce the complexity by using two pointers instead of binary search. We can consider all possible $$$(j, x)$$$ and then use two pointer approach to find optimal $$$y$$$ for each $$$i$$$. For each pair $$$(j, x)$$$, we perform $$$O(\mathbf{N})$$$ operations. Hence, the overall complexity of the solution is $$$O(\mathbf{N}^{3})$$$.
Test set 3
For this test set, we can store the optimal second subarray length for each sum and iterate over each possible first subarray.
Consider the following pseudocode:
for i = 0 to K:
Best[i] = inf
ans = inf
for i = N to 1:
currSum = 0
for j = i to 1:
// |currSum| denotes sum of subarray(j, i).
currSum += B[j]
if currSum <= K:
// Best[K - currSum] denotes the minimum length of subarray starting after index i which has sum equal to K - currSum.
ans = min(ans, j - i + 1 + Best[K - currSum])
currPostSum = 0
for x = i to N:
// |currPostSum| denotes sum of subarray(i, x).
currPostSum += B[x]
if currPostSum <= K:
// Update the minimum length of subarray with sum equal to |currPostSum|.
Best[currPostSum] = min(Best[currPostSum], x - i + 1)
When we are iterating from $$$\mathbf{N}$$$ to $$$1$$$ and are at index $$$i$$$ currently, $$$Best_{S}$$$ stores the minimum length of subarray starting at any index greater than $$$i$$$ and having sum $$$S$$$. Basically, this would denote the optimal length of second subarray with sum $$$S$$$ if we choose first subarray ending at index $$$i$$$. We consider all indexes $$$j$$$ from $$$1$$$ to $$$i$$$. If sum of subarray $$$(j,i)$$$ is $$$currSum$$$ (such that $$$currSum \le \mathbf{K}$$$), we update the answer. Then, we update the minimum length for each sum for the subarrays starting at index $$$i$$$. We do this by iterating for $$$x$$$ from $$$i$$$ to $$$\mathbf{N}$$$. If sum of $$$subarray(i,x)$$$ is $$$currPostSum$$$, then update $$$Best_{currPostSum}=min(Best_{currPostSum}, x - i + 1)$$$. As $$$K \le 10^{6}$$$, we can maintain an array for storing $$$Best$$$. This would allow updating and looking up the sum in $$$O(1)$$$ time. For each index we do $$$O(\mathbf{N})$$$ operations, hence the overall complexity is $$$O(\mathbf{N}^2 + \mathbf{K})$$$.
Analysis — D. Simple Polygon
According to Pick's theorem, the
area of a simple polygon having integer vertex coordinates is $$$Area=i+\frac{b}{2}-1$$$, where
$$$i$$$ is the number of integer points inside the polygon and $$$b$$$ is the number of integer
points on its border. If we double this area, as in our problem statement, it follows that
$$$\mathbf{A}=2 \times Area = 2i+b-2$$$. Since $$$i \ge 0$$$ and $$$b \ge \mathbf{N}$$$, a lower bound on the
'doubled-area' $$$\mathbf{A}$$$ of a
polygon with $$$\mathbf{N}$$$ vertices is $$$\mathbf{A}=2i+b-2 \ge \mathbf{N}-2$$$. Therefore, if $$$\mathbf{A} \lt \mathbf{N}-2$$$, the
answer is IMPOSSIBLE. In what follows, we will show that this is a
tight
lower bound by constructing an $$$\mathbf{N}$$$ vertex simple polygon having a 'doubled-area' $$$\mathbf{A}$$$ for any given
$$$\mathbf{A} \ge \mathbf{N}-2$$$.
Test Set 1
There are many ways to construct the necessary polygons. The following drawing shows possible constructions for $$$3 \le \mathbf{N} \le 5$$$.
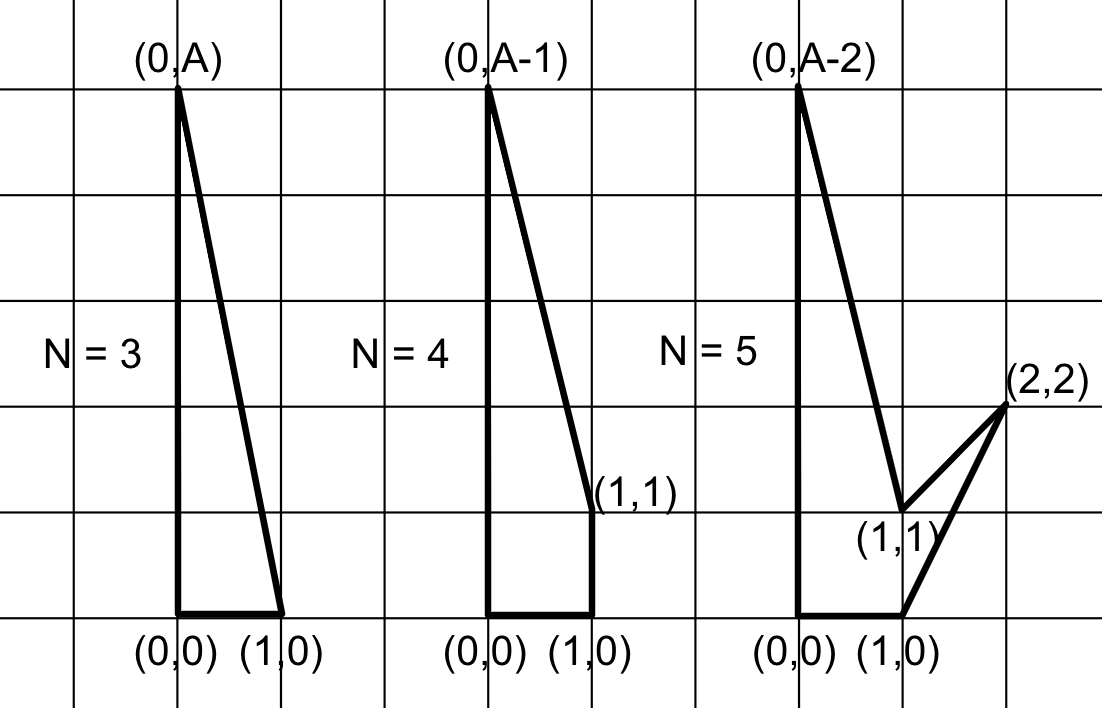
These polygons have no internal integer points, therefore, by Pick's theorem, their 'doubled-area' is $$$b-2$$$. For example, for $$$\mathbf{N}=5$$$, we can verify that $$$b=\mathbf{A}+2$$$ by counting the integer points on the border. Therefore, the 'doubled-area' is $$$b-2=\mathbf{A}+2-2=\mathbf{A}$$$, which validates our construction. Similarly, it can be verified that we have achieved the desired area for $$$\mathbf{N}=3$$$ and $$$\mathbf{N}=4$$$ as well.
The time complexity of the construction is $$$O(1)$$$.
Test Set 2
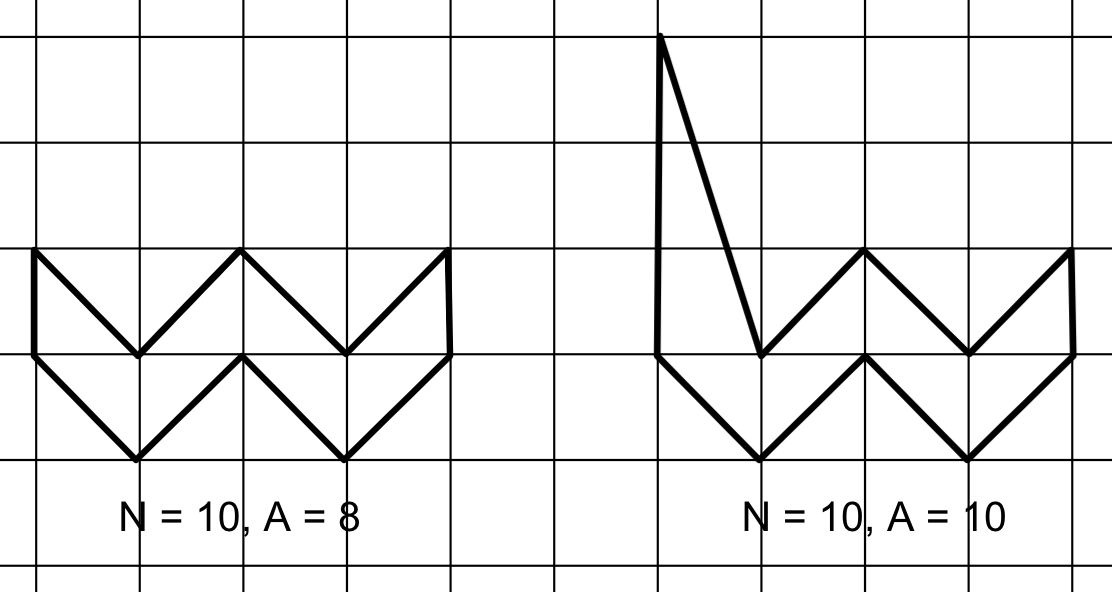
For $$$\mathbf{N} \gt 5$$$, the construction is a little more involved. Let us start with the base case, where the 'doubled-area' of the polygon is the smallest possible, namely, $$$\mathbf{N}-2$$$. The following drawing illustrates the construction for $$$6 \le \mathbf{N} \le 10$$$, but it can be generalized for arbitrary $$$\mathbf{N}$$$ by extending the zig-zag shape to the right.
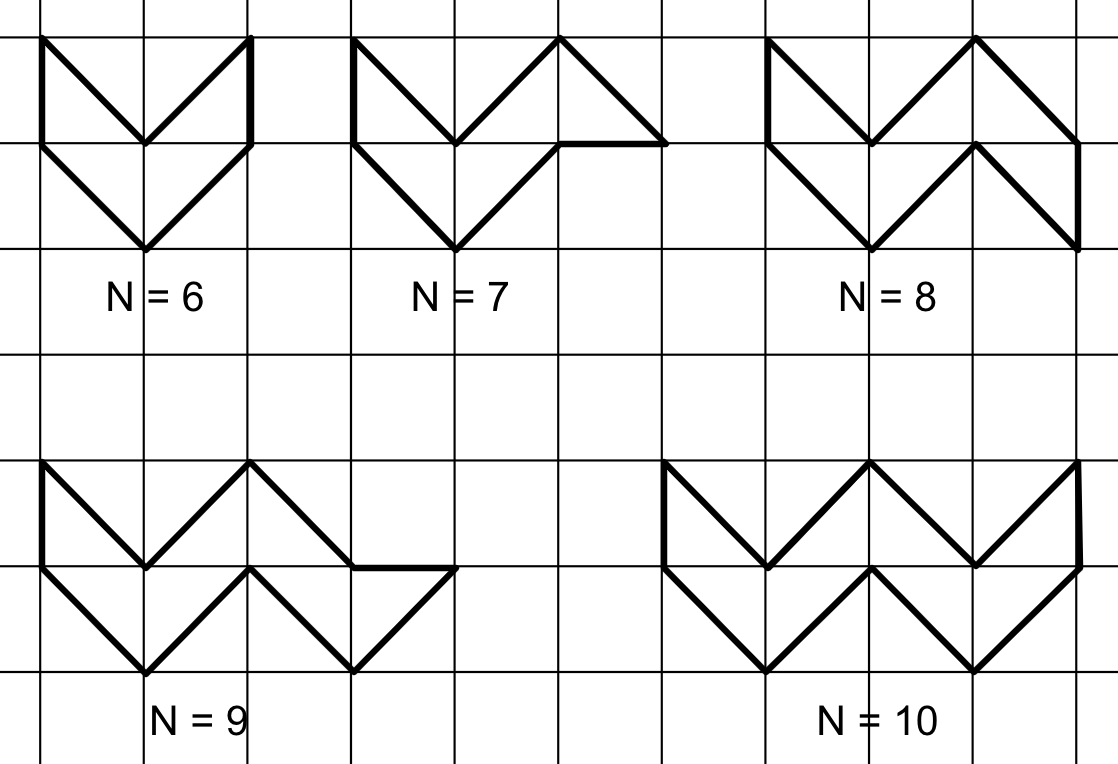
The base polygon has $$$\mathbf{N}$$$ integer points on the border and no internal integer points, therefore, its 'doubled-area' is $$$\mathbf{N}-2$$$. If $$$\mathbf{A} \gt \mathbf{N}-2$$$, we just need to introduce $$$\mathbf{A}-\mathbf{N}+2$$$ more points on the border by say, lifting the top-left vertex up $$$\mathbf{A}-\mathbf{N}+2$$$ units as shown in the following drawing for $$$\mathbf{N}=10$$$ and $$$\mathbf{A}=10$$$.
The time complexity of the construction is $$$O(\mathbf{N})$$$.