Google Kick Start Archive — Round F 2021 problems
Overview
Thank you for participating in Kick Start 2021 Round F!
Cast
Trash Bins: Written by Bartosz Kostka and prepared by Jennifer Zhou.
Star Trappers: Written by Fahim Ferdous Neerjhor and prepared by Jennifer Zhou.
Festival: Written by Anurag Singh and prepared by Swapnil Mahajan.
Graph Travel: Written by Sean Jin and prepared by Junyang Jiang.
Solutions, other problem preparation, reviews and contest monitoring by Aditya Ghosh, Akul Siddalingaswamy, Aneesh D H, Ankit Goyal, Anurag Singh, Bartosz Kostka, Bohdan Pryshchenko, Dee Guo, Deepak Gour, Eric Dong, Fahim Ferdous Neerjhor, Harshil Shah, Jakub Kuczkowiak, Jared Gillespie, Jayant Sharma, Jennifer Zhou, Junyang Jiang, Kashish Bansal, Lizzie Sapiro Santor, Lucas Maciel, Maks Verver, Maneeshita Sharma, Michał Łowicki, Mo Luo, Nikolai Artemiev, Phil Sun, Pranav Raj, Ruoyu Zhang, Samiksha Gupta, Sanyam Garg, Sarah Young, Sasha Fedorova, Sean Jin, Sera Wang, Shweta Karwa, Swapnil Gupta, Swapnil Mahajan, Teja Vardhan Reddy Dasannagari, Umang Goel, Vijay Krishan Pandey, Wendi Wang.
Analysis authors:
- Trash Bins: Maneeshita Sharma
- Star Trappers: Maks Verver
- Festival: Lucas Maciel
- Graph Travel: Deepak Gour
A. Trash Bins
Problem
In the city where you live, Kickstartland, there is one particularly long street with $$$\mathbf{N}$$$ houses on it. This street has length $$$\mathbf{N}$$$, and the $$$\mathbf{N}$$$ houses are evenly placed along it, that is, the first house is at position $$$1$$$, the second house is at position $$$2$$$, and so on. The distance between any pair of houses $$$i$$$ and $$$j$$$ is $$$|i-j|$$$, where $$$|x|$$$ denotes the absolute value of $$$x$$$.
Some of these houses have trash bins in front of them. That means that the owners of such houses do not have to walk when they want to take their trash out. However, for the owners of houses that do not have trash bins in front of them, they have to walk towards some house that has a trash bin in front of it, either to the left or to the right of their own house.
To save time, every house owner always takes their trash out to the trash bin that is closest to their houses. If there are two trash bins that are both the closest to a house, then the house owner can walk to any of them.
Given the number of houses $$$\mathbf{N}$$$, and the description of which of these houses have trash bins in front of them, find out what is the sum of the distances that each house owner has to walk to take their trashes out. You can assume that at least one house has a trash bin in front of it.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow. Each test case consists of two lines.
The first line of each test case contains an integer $$$\mathbf{N}$$$, denoting the number of houses on the street.
The second line of each test case contains a string $$$\mathbf{S}$$$ of length $$$\mathbf{N}$$$, representing which houses have trash bins in front of them. If the $$$i$$$-th character in string $$$\mathbf{S}$$$ is equal to $$$1$$$, then it means that the $$$i$$$-th house has a trash bin in front of it. Otherwise, if it is equal to $$$0$$$, then it means that the $$$i$$$-th house does not have a trash bin in front of it.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$,
where $$$x$$$ is the test case number (starting from 1) and $$$y$$$ is
the sum of the distances that each house owner has to walk to take their trashes out.
Limits
Time limit: 20 seconds.
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
The length of $$$\mathbf{S}$$$ is equal to $$$\mathbf{N}$$$.
Each character of $$$\mathbf{S}$$$ is either $$$0$$$ or $$$1$$$.
There is at least one character $$$1$$$ in $$$\mathbf{S}$$$.
Test Set 1
$$$1 \le \mathbf{N} \le 100$$$.
Test Set 2
$$$1 \le \mathbf{N} \le 5 \times 10^5$$$.
Sample
2 3 111 6 100100
Case #1: 0 Case #2: 5
For the first test case, every house has a trash bin in front of it, and therefore none of the house owners will have to walk to take their trashes out.
For the second test case, the first and the fourth house owners have trash bins in front of their houses, and therefore will not have to walk. The second house owner will walk towards the first house, and the distance will be equal to $$$1$$$. The third, fifth, and sixth house owners will walk towards the fourth house, and the distances will be equal to $$$1$$$, $$$1$$$, and $$$2$$$, respectively.
B. Festival
Problem
You have just heard about a wonderful festival that will last for $$$\mathbf{D}$$$ days, numbered from $$$1$$$ to $$$\mathbf{D}$$$. There will be $$$\mathbf{N}$$$ attractions at the festival. The $$$i$$$-th attraction has a happiness rating of $$$\mathbf{h_i}$$$ and will be available from day $$$\mathbf{s_i}$$$ until day $$$\mathbf{e_i}$$$, inclusive.
You plan to choose one of the days to attend the festival. On that day, you will choose up to $$$\mathbf{K}$$$ attractions to ride. Your total happiness will be the sum of happiness ratings of the attractions you chose to ride.
What is the maximum total happiness you could achieve?
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow.
The first line of each test case contains the three integers, $$$\mathbf{D}$$$, $$$\mathbf{N}$$$ and $$$\mathbf{K}$$$. The next $$$\mathbf{N}$$$ lines describe the attractions. The $$$i$$$-th line contains $$$\mathbf{h_i}$$$, $$$\mathbf{s_i}$$$ and $$$\mathbf{e_i}$$$.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$,
where $$$x$$$ is the test case number (starting from 1) and $$$y$$$ is the maximum total happiness you could achieve.
Limits
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$1 \le \mathbf{K} \le \mathbf{N}$$$.
$$$1 \le \mathbf{s_i} \le \mathbf{e_i} \le \mathbf{D}$$$, for all $$$i$$$.
$$$1 \le \mathbf{h_i} \le 3 \times 10^5$$$, for all $$$i$$$.
Test Set 1
Time limit: 20 seconds.
$$$1 \le \mathbf{N} \le 1000$$$.
$$$1 \le \mathbf{D} \le 1000$$$.
Test Set 2
Time limit: 90 seconds.
For at most $$$10$$$ test cases:
- $$$1 \le \mathbf{N} \le 3 \times 10^5$$$.
- $$$1 \le \mathbf{D} \le 3 \times 10^5$$$.
For the remaining cases, $$$1 \le \mathbf{N}, \mathbf{D} \le 1000$$$.
Sample
2 10 4 2 800 2 8 1500 6 9 200 4 7 400 3 5 5 3 3 400 1 3 500 5 5 300 2 3
Case #1: 2300 Case #2: 700
In sample test case 1, the festival lasts $$$\mathbf{D} = 10$$$ days, there are $$$\mathbf{N} = 4$$$ attractions, and you can ride up to $$$\mathbf{K} = 2$$$ attractions.
If you choose to attend the festival on the 6th day, you could ride the first and second attractions for a total happiness of $$$800 + 1500 = 2300$$$. Note that you cannot also ride the third attraction, since you may only ride up to $$$\mathbf{K} = 2$$$ attractions. This is the maximum total happiness you could achieve, so the answer is $$$2300$$$.
In sample test case 2, the festival lasts $$$\mathbf{D} = 5$$$ days, there are $$$\mathbf{N} = 3$$$ attractions, and you can ride up to $$$\mathbf{K} = 3$$$ attractions.
If you choose to attend the festival on the 3rd day, you could ride the first and third attractions for a total happiness of $$$400 + 300 = 700$$$. This is the maximum total happiness you could achieve, so the answer is $$$700$$$.
C. Star Trappers
Problem
John and Ada are sitting on the grass above a small hill. It is midnight and the sky is full of stars. The sky looks like a 2D plane from so far away and the stars look like points on that plane. Ada loves blue stars and suddenly she notices one, while all the other stars in the sky are white. She loves the blue star so much that she wants to trap it. And she asks John for help.
Ada will tell John the position of the blue star and he has to trap it. To trap it, John has to draw a polygon in the sky with his buster sword, so that the blue star is strictly inside the polygon (not on the border of the polygon) and the polygon has the smallest possible perimeter. The vertices of the polygon must be the white stars.
Even though John is super awesome, he needs your help. Given the positions of the white stars and the blue star, you need to find out whether John can trap the blue star and if he can, also find the minimum length of the perimeter of the polygon he will use.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow.
For each test case, the first line contains an integer $$$\mathbf{N}$$$, it denotes the number of white stars
in the sky.
The next $$$\mathbf{N}$$$ lines will each contain two integers, $$$\mathbf{X_i}$$$ and $$$\mathbf{Y_i}$$$. The
$$$i$$$-th pair of integers denotes the x and y coordinates of the $$$i$$$-th star
in the sky.
After these $$$\mathbf{N}$$$ lines, there will be one last line, which will contain two integers,
$$$\mathbf{X_s}$$$ and $$$\mathbf{Y_s}$$$, which denote the x and y coordinates of the
blue star.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$,
where $$$x$$$ is the test case number (starting from 1) and $$$y$$$ is the minimum length of the
perimeter of the polygon drawn to trap the shooting star. If it is impossible for John to draw a
polygon that traps the star, then $$$y$$$ should be IMPOSSIBLE.
$$$y$$$ will be considered correct if it is within an absolute or relative error of $$$10^{-6}$$$ of the correct answer. See the FAQ for an explanation of what that means, and what formats of real numbers we accept.
Limits
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$0 \le \mathbf{X_i}, \mathbf{Y_i} \le 10^{6}$$$, for all $$$i$$$.
$$$0 \le \mathbf{X_s}, \mathbf{Y_s} \le 10^{6}$$$.
No two stars (including the blue star) will have the same position.
Test Set 1
Time limit: 5 seconds.
$$$1 \le \mathbf{N} \le 10$$$.
Test Set 2
Time limit: 5 seconds.
$$$1 \le \mathbf{N} \le 45$$$.
Test Set 3
Time limit: 50 seconds.
For at most 10 test cases:
$$$1 \le \mathbf{N} \le 300$$$.
For the remaining test cases:
$$$1 \le \mathbf{N} \le 60$$$.
Sample
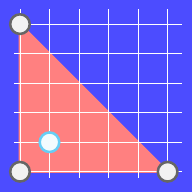
2 2 0 0 5 0 2 2 3 0 0 5 0 0 5 1 1
Case #1: IMPOSSIBLE Case #2: 17.071068
In the first test case we have only two white stars, so we cannot draw any polygons.
In the second test case we have three white stars, so we can draw only one polygon (a triangle), as shown in the picture below. It turns out that we are able to catch the blue star in this polygon. The length of the perimeter of this polygon is $$$5 + 5 + 5\sqrt{2} \approx 17.071068$$$.
D. Graph Travel
Problem
Ada lives in a magic country A, and she is studying at Magic University. Today, Ada wants to collect magic points in a special space.
The space has $$$\mathbf{N}$$$ rooms $$$(0, 1, \dots, \mathbf{N}-1)$$$. There are $$$\mathbf{M}$$$ corridors connecting the rooms. A corridor $$$j$$$ connects room $$$\mathbf{X_j}$$$ and room $$$\mathbf{Y_j}$$$, meaning you can travel between the two rooms.
The $$$i$$$-th room contains $$$\mathbf{A_i}$$$ magic points and is protected by a magic shield with properties $$$\mathbf{L_i}$$$ and $$$\mathbf{R_i}$$$. To enter the $$$i$$$-th room, first you need to get to any room adjacent to the $$$i$$$-th room (i.e. connected to it by a corridor) through rooms with already broken shields. Then you have to break the shield to this room, but you can break the shield if and only if you have between $$$\mathbf{L_i}$$$ and $$$\mathbf{R_i}$$$ magic points, inclusive. After you break the shield, you will enter the room and automatically collect the $$$\mathbf{A_i}$$$ magic points assigned to this room. The room will not generate new magic points. The room will also not generate a new shield after it is broken, so you can freely go back to every room with already broken shields regardless of the amount of points you have.
Ada starts with $$$0$$$ magic points and her goal is to find a way to collect exactly $$$\mathbf{K}$$$ magic points. She can start in any room, and end in any room. The room she chooses to start in will automatically have its magic shield broken, and she will automatically collect all the magic points from this room.
After inspecting the map of the rooms and corridors, Ada thinks the task is very easy, so she wants to challenge herself with a more difficult task. She wants to know how many unique ways there are to reach the goal. Two ways are different if their unique paths are different. The unique path is the order of rooms in which she broke the shields, e.g.: if you visit the rooms in the order $$$(1, 3, 2, 1, 3, 5, 3, 6)$$$, the unique path is $$$(1, 3, 2, 5, 6)$$$.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow.
For each test case, the first line contains three integers $$$\mathbf{N}$$$, $$$\mathbf{M}$$$, and $$$\mathbf{K}$$$: the number of rooms, the numbers of corridors, and the numbers of magic points we want to collect, respectively.
The next $$$\mathbf{N}$$$ lines contain three integers $$$\mathbf{L_i}$$$, $$$\mathbf{R_i}$$$, and $$$\mathbf{A_i}$$$: The magic shield properties $$$\mathbf{L_i}$$$ and $$$\mathbf{R_i}$$$ of room $$$i$$$, and the number of magic points $$$\mathbf{A_i}$$$, respectively.
The next $$$\mathbf{M}$$$ lines contain two integers $$$\mathbf{X_j}$$$ and $$$\mathbf{Y_j}$$$: the rooms that are connected by corridor $$$j$$$.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$, where $$$x$$$ is the test case number (starting from 1) and $$$y$$$ is the number of ways to collect $$$\mathbf{K}$$$ magic points.
Limits
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$0 \le \mathbf{M} \le \frac{N \times (N-1)}{2}$$$.
$$$\mathbf{0} \le \mathbf{X_j}, \mathbf{Y_j} \le \mathbf{N-1}$$$.
$$$\mathbf{X_j} \neq \mathbf{Y_j}$$$
Each pair of rooms can be connected by at most one corridor.
Test Set 1
Time limit: 20 seconds.
$$$1 \le \mathbf{N} \le 8$$$.
$$$1 \le \mathbf{K} \le 100$$$.
$$$0 \le \mathbf{L_i} \le \mathbf{R_i} \le 50$$$.
$$$1 \le \mathbf{A_i} \le 50$$$.
Test Set 2
Time limit: 60 seconds.
$$$1 \le \mathbf{N} \le 15$$$.
$$$1 \le \mathbf{K} \le 2 \times 10^9$$$.
$$$0 \le \mathbf{L_i} \le \mathbf{R_i} \le 10^9$$$.
$$$1 \le \mathbf{A_i} \le 10^9$$$.
Sample
3 4 3 3 1 3 1 1 1 1 2 4 1 2 3 1 0 1 1 2 2 3 4 5 3 1 3 1 1 1 1 2 4 1 2 3 1 0 1 1 2 2 3 3 0 0 2 4 1 2 0 4 1 0 4 1 0 4 2 0 4 2 0 1
Case #1: 4 Case #2: 8 Case #3: 4
In the first case, there are $$$4$$$ different ways. They are:
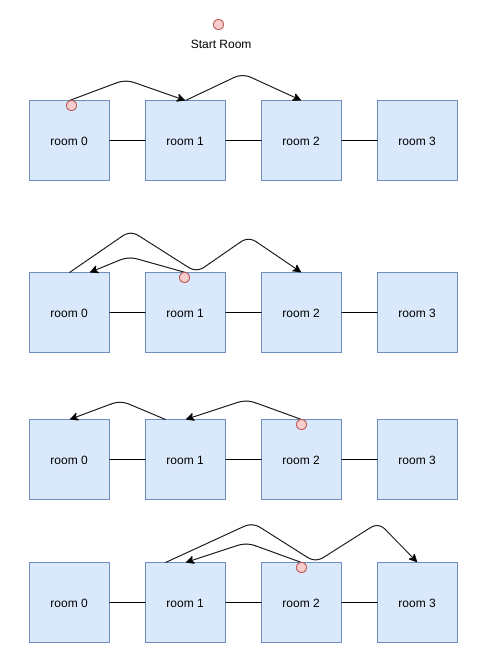
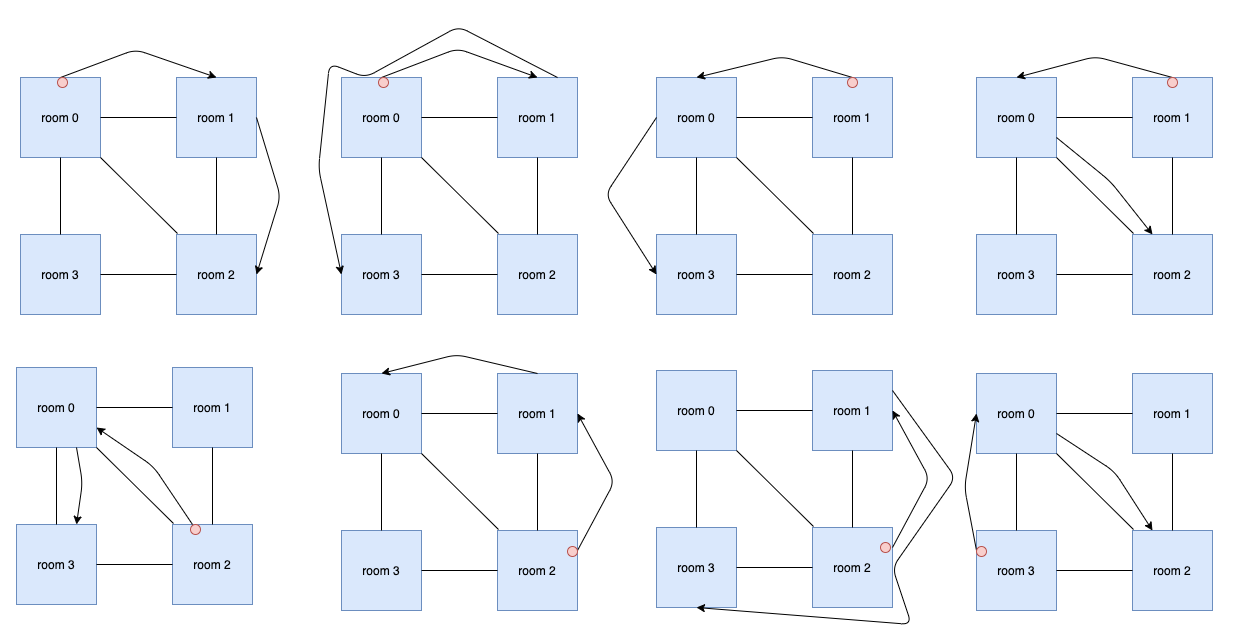
In the second case, there are $$$8$$$ different ways. They are:
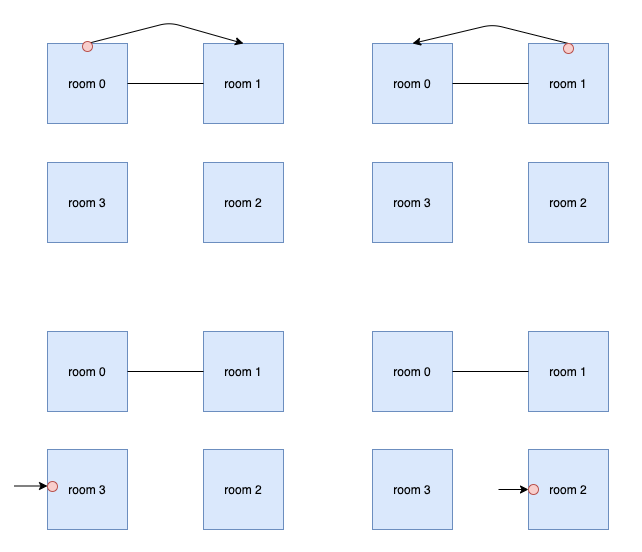
In the third case, there are $$$4$$$ different ways. They are:
Analysis — A. Trash Bins
For every house, we have to find the closest house with a trash bin. This can either be the same house, or some other house to its left or right as at least one house has a trash bin in front of it.
Let $$$F(i)$$$ denote distance that the $$$i$$$-th house owner has to walk to take their trashes out. The final answer is $$$\displaystyle\sum_{i=1}^{\mathbf{N}} F(i) $$$.
Test Set 1
For $$$i$$$-th house, we find $$$F(i)$$$ by iterating over all the houses and picking the house $$$j$$$ such that $$$\mathbf{S}_{j}=1$$$ and the distance between the house $$$i$$$ and $$$j$$$ is least.
Complexity : $$$O(\mathbf{N} ^ 2)$$$ per test case
Test Set 2
For $$$i$$$-th house, let $$$L(i)$$$ denote the closest house to its left which has trash bin in front of it and $$$R(i)$$$ denote the closest house to its right with a trash bin in front of it. We can find $$$L(i)$$$ and $$$R(i)$$$ for all the houses in one linear pass.
$$$L(i) = \begin{cases} -\infty & \quad \text{if } i = 1\\ i-1 & \quad \text{if } i > 1 \text{ and } \mathbf{S}_{i-1} = 1 \\ L(i-1) & \quad \text{if } i > 1 \text{ and } \mathbf{S}_{i-1} = 0 \\ \end{cases}$$$
$$$R(i) = \begin{cases} \infty & \quad \text{if } i = \mathbf{N}\\ i+1 & \quad \text{if } i < \mathbf{N} \text{ and } \mathbf{S}_{i+1} = 1 \\ R(i+1) & \quad \text{if } i < \mathbf{N} \text{ and } \mathbf{S}_{i+1} = 0 \\ \end{cases}$$$
$$$F(i) = \begin{cases} 0 & \quad \text{if } \mathbf{S}_{i} = 1\\ \min({i - L(i), R(i) - i}) & \quad \text{if } \mathbf{S}_{i} = 0\\ \end{cases}$$$
You might have to deal with overflow issues depending on the data types used as the maximum value of answer does not fit 32-bit integer data types.
You can take $$$\infty$$$ as any value $$$ >= 2 \times \mathbf{N}$$$.
Complexity : $$$O(\mathbf{N})$$$ per test case
Analysis — B. Festival
Test Set 1
We can consider each attraction as an interval that covers some range of days and has some
happiness rating.
Let us denote happiness rating of an interval as HR.
At first we sort the intervals according to their HRs, from higher to lower.
Then we will iterate through each day and consider that day as the day we will attend the
festival. Let us denote this day as $$$d_i$$$. And let us denote the total happiness of upto $$$\mathbf{K}$$$
intervals on this day as $$$c_i$$$.
Let us set $$$c_i$$$ to $$$0$$$. Now we will iterate through the sorted intervals and check if
$$$d_i$$$ is included in the current interval. If yes, then we add the HR of that
interval to $$$c_i$$$. If no, we continue to the next interval. If the number of intervals taken
into account reaches $$$\mathbf{K}$$$, we stop calculating $$$c_i$$$ and compare it to the current maximum
answer and store it as maximum if it is greater. If we iterate through all the intervals and the
number of intervals taken is less than $$$\mathbf{K}$$$, we still compare $$$c_i$$$ to the current maximum
answer and store it as maximum if it is greater.
The answer is the maximum among all $$$c_i$$$s.
The time complexity of this solution is $$$O(\mathbf{N} \times \log{\mathbf{N}} + \mathbf{D} \times \mathbf{N})$$$.
The space complexity (without considering the input) of this solution is $$$O(1)$$$ as no extra
memory is used.
A pseudocode would look something like this:
ans = 0
sort(intervals) // from higher to lower
for d_i = 1 to D:
c_i = 0
cnt = 0
for j = 1 to N:
if (cnt == K): break
if (s_j <= d_i <= e_j):
c_i += h[d_i]
cnt++
ans = max(ans, c_i)
return ans
Test Set 2
Now the brute force will not work. We can still iterate through each day, but now we cannot check
each interval to see if this day is in that interval or not. Rather for each day, we will update
the events taking place on that day efficiently and then calculate the total HR for that day. We
will consider the ending days as the ($$$\mathbf{e_i}$$$ + 1)-th days, because the $$$\mathbf{e_i}$$$-th day is
included in the interval. So now we will consider the ($$$\mathbf{e_i}$$$ + 1)-th day as the ending day
for each interval. For example, if an interval ended on day $$$6$$$ previously, now we will
consider that it ends on day $$$7$$$.
For each day, we will store the intervals that either start or end on that day.
We will use segment trees for our solution. Each leaf node of the tree will be an interval and
the intervals will be sorted according to their HRs, from higher to lower. Initially every
interval will have a value of $$$0$$$. When an interval becomes active, we will update that index
with its HR. And when an interval becomes inactive, we will update that index with $$$0$$$ again.
We need to query the sum of any range in the trees. We also need another operation. At any moment
we need to find the index of the $$$\mathbf{K}$$$-th maximum (HR wise) active interval. If there are less than
$$$\mathbf{K}$$$ active intervals, we will return the index of the rightmost/last active interval. We can use
another segment tree for this.
Now we will iterate through the days.
If the current day is a starting day for an interval, it means this interval has become active.
We will update its index with its HR in one tree and will make it active in the other one.
If the current day is an ending day for an interval, it means this interval has become inactive.
We will update its index with $$$0$$$ in one tree and will make it inactive in the other one.
We will do this for each interval for which the current day is a starting day or an ending
day.
On the days that we update the segment trees, after updating, we will query for the index of the
$$$\mathbf{K}$$$-th maximum active interval in the second tree. Let us assume this index is $$$idx$$$. And then
in the first tree, we will query the sum from the $$$0$$$-th index to index $$$idx$$$. We will
store this sum in the current answer if the current answer is smaller.
The answer is the final value in the current answer.
The time complexity of building a segment tree with $$$n$$$ elements is $$$O(n)$$$ and for
updating and querying the time complexity is $$$O(\log{n})$$$ for each operation.
So the time complexity of this solution is
$$$O(\mathbf{N} + \mathbf{D} + \mathbf{N} \times \log{\mathbf{N}})$$$.
And the space complexity of this solution is $$$O(\mathbf{N})$$$.
Alternative Solution
We will discuss another solution using
multisets which is available in
C++ standard template library (STL). It can also be implemented using a
binary search tree in any
language.
We will use two multisets, one to keep track of the $$$\mathbf{K}$$$ active intervals with higher HRs, and the
other one to keep track of the rest of the active intervals.
Now we will iterate through the days again.
If the current day is a starting day of an interval, then if the number of active intervals in the
first multiset is less than $$$\mathbf{K}$$$, we insert this interval in the first multiset. Otherwise, if the
interval with the smallest HR has a greater HR than this interval, then we insert this interval
in the second multiset. And if it is less or equal, then we remove the smallest from the first
multiset and insert the removed interval into the second multiset. And then we insert the current
interval in the first multiset.
If the current day is an ending day of an interval, then if this interval is in the second
multiset, we simply remove it from there. Otherwise it is in the first multiset. So, we remove the
current interval from the first multiset. Then we remove the interval with the largest HR from the
second multiset and insert the removed interval in the first multiset.
We always maintain a variable $$$sum$$$ which is the sum of the HRs of the intervals in the first
multiset. While inserting/removing an interval in/from the first multiset, we have to update the
value of the $$$sum$$$ accordingly.
The answer is the maximum value of $$$sum$$$ across the whole time.
The time complexity of accessing, inserting, removing elements from a multiset with $$$n$$$
elements is $$$O(\log{n})$$$ for each operation. Since there are $$$\mathbf{N}$$$ intervals and each
interval will be handled $$$2$$$ times and each handling will require $$$O(1)$$$ operations with
the multisets, the overall complexity of all operations with multisets will be
$$$O(\mathbf{N} \times \log{\mathbf{N}})$$$.
So, the overall complexity of this solution is: $$$O(\mathbf{D} + \mathbf{N} \times \log{\mathbf{N}})$$$.
And the space complexity of this solution is $$$O(\mathbf{N})$$$.
Analysis — C. Star Trappers
Test Set 1
Say, we have just one polygon and the point we need to capture (called $$$P$$$ henceforth). We need a way to check if that point is inside the polygon or not. This problem is known as Point in Polygon and ray casting is one of the standard ways to solve it. Now, for the first test set, we can generate all possible simple polygons and check the minimum perimeter polygon which contains the point. Following steps show how to generate all simple polygons:
- Generate all distinct permutations from the given set of points (minimum $$$3$$$ points). Treat each permutation as a polygon with points describing consecutive vertices of that polygon.
- For each polygon, if any two edges intersect each other, discard that polygon.
- All remaining permutations will describe all possible simple polygons.
Runtime Analysis: To generate $$$R$$$ distinct permutations from
$$$\mathbf{N}$$$ points will take $$$\mathbf{N}$$$ permutations $$$R$$$ (called $$$\mathrm{P}^{\mathbf{N}}_R$$$)
and then checking for intersection of any two edges will take $$$(R - 1) \times
(R - 2)$$$. Then for each polygon it will take $$$(R - 1)$$$ checks for ray
casting. So, total runtime will be:
$$$O(\sum_{R=3}^{\mathbf{N}}\mathrm{P}^{\mathbf{N}}_R \times (R - 1) \times (R - 2) \times (R
- 1) = O(\sum_{R=3}^{\mathbf{N}}\mathrm{P}^{\mathbf{N}}_R \times R^3) = O(\mathbf{N}! \times
\mathbf{N}^3)$$$.
Note: This might look like it will TLE but most of the checks would not be
performed. We can improve this runtime, though, using convex
hull. A convex hull of a simple polygon will always include the initial
area of a simple polygon and will have smaller or equal perimeter. The runtime
in that case will be:
$$$O(\sum_{R=3}^{\mathbf{N}}\mathrm{C}^{\mathbf{N}}_R \times (R \times log(R)) \times (R - 1))
= O(2^\mathbf{N} \times \mathbf{N}^2 \times log(\mathbf{N}))$$$
Test Set 2
Notice that if a point is inside a polygon with more than $$$4$$$ points, we can reduce it to a triangle ($$$ABC$$$ in the image below) or a quadrilateral ($$$ABCD$$$ in the image below) which contains the point.
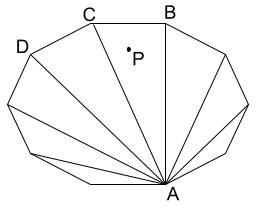
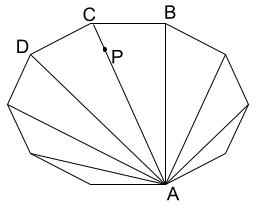
Note: It can be some other triangle/quadrilateral in the above polygon, the image is just for illustration.
So, we can generate all possible quadrilaterals and triangles and then check the minimum perimeter polygon which contains the point.
Runtime Analysis: We can generate all sets of points with set size being $$$4$$$ (for quadrilateral) and $$$3$$$ (for triangle) from the given set of points taking $$$O(\mathbf{N}^4 + \mathbf{N}^3) = O(\mathbf{N}^4)$$$. Checking "Point in Polygon" in this case will be constant time.
Test Set 3
The observation required for this set is that if the point $$$P$$$ is on one of the diagonals in the quadrilateral, it must be at the intersection of the diagonals. If it is not, then we can reduce the quadrilateral to a triangle with a lesser perimeter (as in the following diagram, quadrilateral $$$ABCD$$$ can be reduced to triangle $$$ABC$$$).
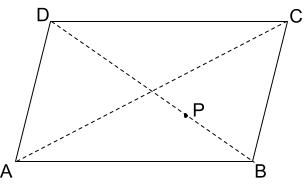
Another observation is that among the points collinear to $$$P$$$ only one point
closest to $$$P$$$ on both side matters. Other points will always create
quadrilateral with larger perimeter. So, all collinear segments of interest are
unique.
So, for this set we can check all the triangles first. Then to generate
quadrilaterals, we can find the diagonals as:
- Find polar angles of all points, treating $$$P$$$ as origin.
- Group all points with same polar angles in one equivalence class.
- Choose the point closest to $$$P$$$ in each equivalence class and discard rest of the points.
- Now, generate line segments from the remaining points. For each polar angle between $$$[0, \pi)$$$ radians (called $$$\theta$$$), check if we have a point at $$$\theta + \pi$$$. These two points make one line segment (note that $$$P$$$ lies on this segment).
- These line segments are treated as diagonals of the quadrilateral.
Runtime Analysis: The triangle case remains the same, taking
$$$O(\mathbf{N}^3)$$$. For quadrilateral, we will generate at most $$$\mathbf{N} / 2$$$ sets
of points in $$$O(\mathbf{N})$$$ and then we can check all combinations of these
segments for possible quadrilateral candidates in $$$O((\mathbf{N}/2)^2)$$$. So, total
runtime will be:
$$$O(\mathbf{N}^3 + \mathbf{N} + (\mathbf{N}/2)^2) = O(\mathbf{N}^3)$$$
Analysis — D. Graph Travel
Test Set 1
We use a brute force strategy by DFS:- Pick a room to start. Add it to the path and save the path as visited. If we have $$$\mathbf{K}$$$ points, increment our paths counter.
- Pick a room outside the path that keeps our total points under $$$\mathbf{K}$$$. Check if any coordidor connects the room to another room in the path. If yes, add the new connected room to the path and remove the corridor from the set. If no, try the next room outside the path. Evaluating each room choice requires checking every corridor and takes $$$O(\mathbf{M})$$$ time.
- If we are out of corridors or our total points $$$\ge \mathbf{K}$$$, we backtrack. Remove the latest room from the path, and try the next available corridor.
Test Set 2
Brute force is not good enough. We approach this problem with dynamic programming. Our strategy will be the following:- Find the total magic points of every combination of rooms regardless of whether they can be visited.
- For each combination of rooms, determine if a room can be visited as a new room.
- Use dynamic programming to determine which combinations can actually be visited given any single room as a starting point.
- Filter down to room combinations with point total $$$\mathbf{K}$$$ that can be visited.
There are $$$2^\mathbf{N}$$$ different ways to pick combinations of rooms. Let us first assume that it is possible to visit that combination of rooms and calculate the total magic points. Since there are $$$2^\mathbf{N}$$$ possible combinations, we can express each combination as a number whose binary representation tells us whether we visit that room. For example:
- $$$7 = 111$$$ contains rooms $$$1$$$, $$$2$$$, and $$$3$$$
- $$$4 = 100$$$ contains only room $$$3$$$
Next, assume we have just visited a combination of rooms, we want to find out if we are able to visit a particular room and add it as a new unique room.
- If at least one of the rooms in starting combination is adjacent to the new room. To check this, we can maintain a bitmask of rooms adjacent to each room (adjacency bitmask) and then we can check if the starting combination and adjacency bitmask have a common element (this can be done checking that the
ANDof starting combination and adjacency bitmask is non zero). - We have the correct number of points to break that room's shield (say our destination is room $$$i$$$ and we have $$$P$$$ points, this means $$$\mathbf{L_i} \le P \le \mathbf{R_i}$$$).
Now we use dynamic programming. We iterate through all the integers between $$$0$$$ and $$$2^\mathbf{N}$$$, each integer representing a possible combination of rooms. For a combination $$$x$$$, we iterate through every room already in $$$x$$$. We remove a room and check if it is possible to visit that room ($$$i$$$) from the remaining combination ($$$x'$$$) using the $$$canVisit$$$ array ($$$canVisit[x'][i]$$$). The number of ways to visit combination $$$x$$$ is equal to the sum of all the numbers of ways to visit all possible $$$x'$$$. Since we are iterating from smaller combinations up, we know we only need to iterate once. This will tell us which room combinations can be visited. This takes $$$O(2^\mathbf{N} \times \mathbf{N}+\mathbf{M})$$$
Finally, we pick out all the room combinations that have total of $$$\mathbf{K}$$$ points. We filter that down to the combinations that we can actually visit and sum all the unique ways to visit that combination. This just takes $$$O(2^\mathbf{N})$$$ time. Our final run time is $$$O(2^\mathbf{N} \times \mathbf{N}+\mathbf{M})$$$