Google Kick Start Archive — Round E 2021 problems
Overview
Thank you for participating in Kick Start 2021 Round E!
Cast
Shuffled Anagrams: Written by Pablo Heiber and prepared by Swapnil Mahajan.
Birthday Cake: Written by Mohamed Omar and prepared by Laksh Nachiappan.
Palindromic Crossword: Written by Bartosz Kostka and prepared by Attila Toth.
Increasing Sequence Card Game: Written by Yossi Matsumoto and prepared by Swapnil Gupta.
Solutions, other problem preparation, reviews and contest monitoring by Abhishek Saini, Abhishek Singh, Akul Siddalingaswamy, Alexandra Goodman, Aneesh D H, Anik Sarker, Ankit Goyal, Anurag Singh, Anushi Maheshwari, Attila Toth, Bartosz Kostka, Bohdan Pryshchenko, Erick Wong, Gregory Yap, Harshil Shah, Jared Gillespie, Jennifer Zhou, Kashish Bansal, Krists Boitmanis, Laksh Nachiappan, Lizzie Sapiro Santor, Lucas Maciel, Mahmoud Ezzat, Manav Jain, Mohamed Omar, Pablo Heiber, Pranjal Jain, Rudhir Gupta, Ruoyu Zhang, Samiksha Gupta, Sarah Young, Sasha Fedorova, Sera Wang, Sharath Holla, Shweta Karwa, Swapnil Gupta, Swapnil Mahajan, Swetank Modi, Szymon Rzeźnik, Teja Vardhan Reddy Dasannagari, Umang Goel, Utsav Rajpara, Vijay Krishan Pandey, Wajeb Saab, Wei Zhou, Yossi Matsumoto.
Analysis authors:
- Shuffled Anagrams: Sarah Young
- Birthday Cake: Krists Boitmanis
- Palindromic Crossword: Ankit Goyal
- Increasing Sequence Card Game: Ankit Goyal
A. Shuffled Anagrams
Problem
Let $$$\mathbf{S}$$$ be a string containing only letters of the English alphabet. An anagram of $$$\mathbf{S}$$$ is any
string that contains exactly the same letters as $$$\mathbf{S}$$$ (with the same number of occurrences for each
letter), but in a different order. For example, the word kick has anagrams such as kcik and
ckki.
Now, let $$$S[i]$$$ be the $$$i$$$-th letter in $$$\mathbf{S}$$$. We say that an anagram of $$$\mathbf{S}$$$, A, is shuffled
if and only if for all $$$i$$$, $$$S[i] \neq A[i]$$$. So, for instance, kcik is not a shuffled
anagram of kick as the first and fourth letters of both of them are the same. However, ckki
would be considered a shuffled anagram of kick, as would ikkc.
Given an arbitrary string $$$\mathbf{S}$$$, your task is to output any one shuffled anagram of $$$\mathbf{S}$$$, or else print
IMPOSSIBLE if this cannot be done.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow. Each test case consists of one line, a string of English letters.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$,
where $$$x$$$ is the test case number (starting from 1) and $$$y$$$ is a shuffled anagram of the
string for that test case, or IMPOSSIBLE if no shuffled anagram exists for that string.
Limits
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
All input letters are lowercase English letters.
Test Set 1
Time limit: 20 seconds.
$$$1 \le$$$ the length of $$$\mathbf{S}$$$ $$$\le 8$$$.
Test Set 2
Time limit: 40 seconds.
$$$1 \le$$$ the length of $$$\mathbf{S}$$$ $$$\le 10^4$$$.
Sample
2 start jjj
Case #1: tarts Case #2: IMPOSSIBLE
In test case #1, tarts is a shuffled anagram of start as none of the letters in each position of
both strings match the other. Another possible solution is trsta (though you only need to provide one solution).
However, in test case #2, there is no way of anagramming jjj to form a shuffled anagram,
so IMPOSSIBLE is printed instead.
B. Birthday Cake
Problem
You are given a grid of $$$\mathbf{R}$$$ rows and $$$\mathbf{C}$$$ columns that corresponds to a birthday cake.
The rows are numbered from $$$1$$$ to $$$\mathbf{R}$$$ starting from the top.
The columns are numbered from $$$1$$$ to $$$\mathbf{C}$$$ starting from the left.
Each cell in the grid is a square of size $$$1 \times 1$$$.
You noticed that the most delicious part of the cake forms a single filled rectangle;
that means all the cells inside this single rectangle will be delicious as well,
but all the cells outside this rectangle are not delicious.
You have a knife that is long enough to make straight-line cuts of length up to $$$\mathbf{K}$$$.
We want to make a series of cuts to extract each of the delicious cells separately,
so that we can put candles on them, and enjoy the birthday party.
To extract each of the delicious cells separately, they must be disconnected from any other cell.
A cell is disconnected if no other cell is connected to it
in any of the $$$4$$$ directions (up, down, left, right).
A cut is a directed line segment which is valid if the following conditions are met:
- The cut runs along one of the horizontal or vertical lines between the rows and columns of the grid.
- The length of the cut must not exceed $$$\mathbf{K}$$$.
- The starting and ending points of the cut must be grid points (i.e. a corner of a cell). In addition, the starting point must be already exposed, meaning that it lies on one of the $$$4$$$ sides of the grid or on one of the previous cuts.
- The cut must not pass through any other exposed points. It may touch an exposed point, but if it does, it must end right there.
Suppose that $$$\mathbf{K} = 4$$$. Below you can find five examples of valid cuts.
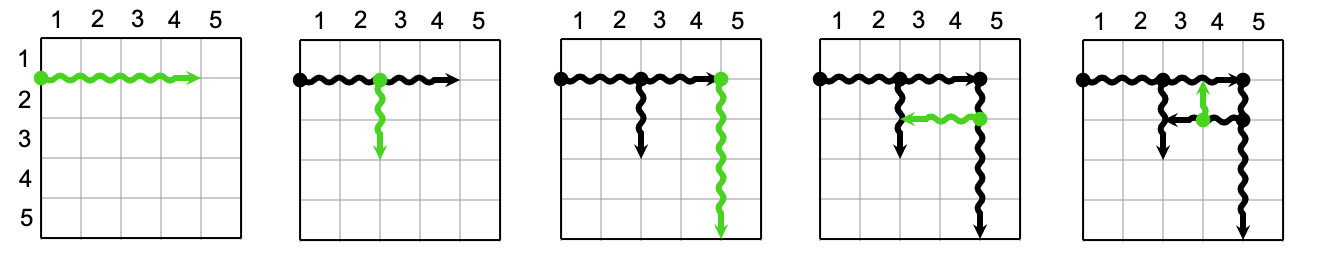
And here are four examples of invalid cuts
- In the first picture, the cut is too long (longer than $$$4$$$).
- In the second picture, the cut starts from an unexposed point (neither one of the $$$4$$$ sides of the grid nor a previous cut).
- In the third picture, the cut passes through an exposed point, it must stop once it touches the exposed point at length $$$2$$$.
- The fourth picture is invalid because of the same reason as the third picture.
We need to find the minimum number of cuts needed to extract all the delicious cells.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow.
Each test case starts with a line containing three integers, $$$\mathbf{R}$$$, $$$\mathbf{C}$$$ and $$$\mathbf{K}$$$.
The next line contains four integers, $$$\mathbf{r_1}$$$, $$$\mathbf{c_1}$$$, $$$\mathbf{r_2}$$$, $$$\mathbf{c_2}$$$,
representing the top-left and bottom-right cell of the delicious rectangle respectively.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$, where $$$x$$$ is
the test case number (starting from 1) and $$$y$$$ is the minimum number of cuts.
Limits
Time limit: 10 seconds.
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$1 \le \mathbf{r_1} \le \mathbf{r_2} \le \mathbf{R}$$$.
$$$1 \le \mathbf{c_1} \le \mathbf{c_2} \le \mathbf{C}$$$.
Test Set 1
$$$1 \le \mathbf{R}, \mathbf{C} \le 100$$$.
$$$\mathbf{K} = 1$$$.
Test Set 2
$$$1 \le \mathbf{R}, \mathbf{C} \le 10^5$$$.
$$$1 \le \mathbf{K} \le 10^5$$$.
Sample
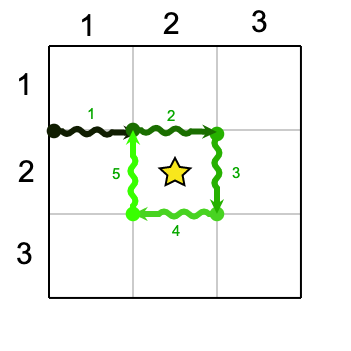
Note: there are additional samples that are not run on submissions down below.1 3 3 1 2 2 2 2
Case #1: 5
Additional Sample - Test Set 2
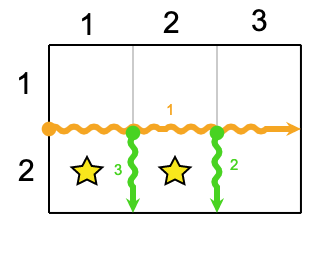
The following additional sample fits the limits of Test Set 2. It will not be run against your submitted solutions.1 2 3 4 2 1 2 2
Case #1: 3
In the Sample Case, the minimum number of cuts is $$$5$$$. One of the possible series of cuts is as follows:
In the Additional Sample Case, the minimum number of cuts is $$$3$$$. One of the possible series of cuts is as follows:
C. Palindromic Crossword
Problem
A crossword puzzle is a
rectangular grid of black cells and letters
A-Z like the one shown below.
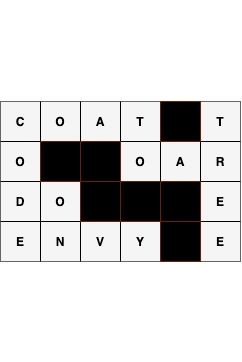
Words in the crossword are defined as maximal vertical or horizontal segments
of characters.
In the crossword
below, DO and ON are examples of words.
A palindromic crossword is one where every word is a
palindrome.
Let $$$\mathbf{R_{i,j}}$$$ represent the character on the $$$i$$$-th row
and $$$j$$$-th column, where $$$i$$$ and $$$j$$$ are $$$1$$$-indexed. The top left corner
is $$$\mathbf{R_{1,1}}$$$.
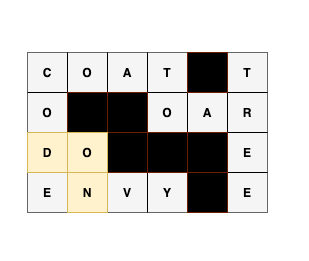
In the example palindromic crossword below, the B in $$$\mathbf{R_{3,2}}$$$
is part of both the horizontal word starting at $$$\mathbf{R_{3,1}}$$$ and the vertical word ending at
$$$\mathbf{R_{4,2}}$$$, and both are palindromes.
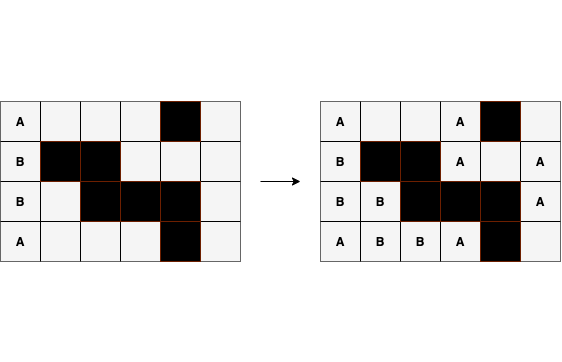
You have been gifted a palindromic crossword puzzle with $$$\mathbf{N}$$$ rows and $$$\mathbf{M}$$$ columns. You finished the crossword and throw away the clues, preparing to hang it on your wall. However, you accidentally erase some of the letters! You want to recover as much of the crossword as possible, but you do not have the clues anymore. Using only the knowledge that the crossword is palindromic, restore the maximum possible number of missing characters in the given crossword.
Missing letters are represented as empty white cells in the below diagram. The crossword on the left is the crossword you are given and the crossword on the right is the result after you recover as many letters as possible. The remaining cells cannot be filled because we do not have sufficient information to recover them.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow.
The first line of each test case contains two
integers, $$$\mathbf{N}$$$ and $$$\mathbf{M}$$$, representing the number of rows and columns in the crossword,
respectively.
The next $$$\mathbf{N}$$$ lines represent the $$$\mathbf{N}$$$ rows of the grid. The $$$i$$$-th row consists of $$$\mathbf{M}$$$ characters
representing $$$\mathbf{R_{i,1}}$$$, $$$\mathbf{R_{i,2}}$$$, $$$\dots$$$, $$$\mathbf{R_{i,M}}$$$. Each character is one of the
following:
- A capital letter of the alphabet (
A-Z) - A period (
.) for a missing letter (empty white cell in the example crossword) - A hash (
#) for black cell
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$
where $$$x$$$ is the test case number (starting from $$$1$$$) and $$$y$$$ is the number of empty white
cells that were filled. Then, output $$$\mathbf{N}$$$ more lines representing the final grid, with
the missing characters (.) replaced by capital letters (A-Z)
where possible.
Limits
Time limit: 60 seconds.
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
There exists at least one way to fill in the given input grid such
that it is a palindromic crossword.
All characters in the grid are in the set $$$\{$$$A-Z, #, .$$$\}$$$
Test Set 1
$$$1 \le \mathbf{N},\mathbf{M} \le 50$$$.
Test Set 2
For at most 10 cases:
$$$1 \le \mathbf{N},\mathbf{M} \le 1000$$$.
For the remaining cases:
$$$1 \le \mathbf{N},\mathbf{M} \le 50$$$.
Sample
2 2 2 A. .# 4 6 A...#. B##... B.###. A...#.
Case #1: 2 AA A# Case #2: 8 A..A#. B##A.A BB###A ABBA#.
In Sample Case #2, we are able to fill in $$$8$$$ of the blanks. We can fill in the missing letters as follows:
A from character at row $$$1$$$, column $$$1$$$.A from row $$$1$$$, column $$$4$$$.A from row $$$2$$$, column $$$4$$$.A from row $$$2$$$, column $$$6$$$.B from row $$$3$$$, column $$$1$$$.B from row $$$3$$$, column $$$2$$$.B from row $$$4$$$, column $$$2$$$.A from row $$$4$$$, column $$$1$$$.D. Increasing Sequence Card Game
Problem
You're playing a card game as a single player.
There are $$$\mathbf{N}$$$ cards. The $$$i$$$-th card has integer $$$i$$$ written on it.
You first shuffle $$$\mathbf{N}$$$ cards randomly and put them in a pile. Take the card at the top of the pile to your hand. Then repeat the following process until the pile becomes empty:
- Check the card on the top of the pile.
- If the number on the card is larger than the number on the last card you took, take the card.
- Otherwise, discard the card.
The score of the game is the number of cards in your hand at the end. With the given number of cards $$$\mathbf{N}$$$, what is the expected score of the game?
Input
The first line of the input contains the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ lines follow. Each line contains a single integer $$$\mathbf{N}$$$, the number of cards in the pile.
Output
For each test case, output one line containing Case #x: y, where x is
the test case number (starting from 1) and y is the expected score at the end of the
game.
y will be considered correct if it is within an absolute or
relative error of 10-6 of the correct answer.
See the FAQ
for an explanation of what that means, and what formats of real numbers we accept.
Limits
Time limit: 20 seconds.
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
Test Set 1
$$$1 \le \mathbf{N} \le 10$$$.
Test Set 2
$$$1 \le \mathbf{N} \le 10^6$$$.
Test Set 3
$$$1 \le \mathbf{N} \le 10^{18}$$$.
Sample
2 1 2
Case #1: 1.0 Case #2: 1.5
Analysis — A. Shuffled Anagrams
Test set 1
For this test set, since the length of $$$\mathbf{S}$$$ $$$\le 8$$$, we can try every permutation of characters and check whether there exists a permutation such that for all $$$i$$$, $$$S[i] \neq A[i]$$$. To find every permutation, we can first convert the string to a character array. Then, we swap the first element with every other element and recursively find permutations of the rest of the string.
This can be performed in $$$O(N!)$$$, where $$$N$$$ is the length of $$$\mathbf{S}$$$.
Test set 2
For this test set, the above solution would exceed the time limits.
The key observation here is that if a character exists more than $$$\lfloor \frac{N}{2} \rfloor$$$ times, then it's impossible to find such a permutation, because at least one position will have a letter that stays the same. Otherwise, we can sort the letters and keep track of the initial position of each letter.
Let the new sorted letters be $$$P$$$. We can split the sorted letters into two halves, from index $$$0$$$ to $$$\frac{N}{2}$$$, $$$P[0:\frac{N}{2}]$$$, and from $$$\frac{N}{2}$$$ to the end, $$$P[\frac{N}{2}:]$$$. If $$$N$$$ is odd, split $$$P$$$ such that the second half has an extra letter, where the first half is $$$0$$$ to $$$\lfloor \frac{N}{2} \rfloor$$$ and the second half is from $$$\lceil \frac{N}{2} \rceil$$$ to the end. Then, we put each character from the second half of the sorted letters $$$P[i + (\frac{N}{2})]$$$ into the original position of the corresponding letter in the first half $$$P[i]$$$. Similarly, we put each character from the first half of the sorted letters $$$P[i]$$$ into the original position of the corresponding letter in the second half $$$P[i + (\frac{N}{2})]$$$. Note that if $$$N$$$ is odd, the second half of the sorted letters $$$P[i + (\frac{N}{2})]$$$ will occupy the first $$$\lfloor \frac{N}{2} \rfloor +1$$$ spaces, while the original first half will occupy the last $$$\lfloor \frac{N}{2} \rfloor $$$ spaces, as shown in the example below. The letter orginally at $$$P[N-1]$$$ will be in the middle of the array after the swap, replacing $$$P[i + \lfloor \frac{N}{2} \rfloor]$$$.
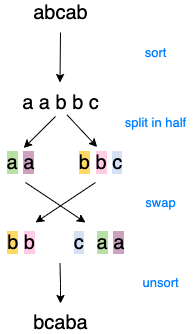
This works because we know that no more than half the characters are equal, and hence the character at $$$P[i]$$$ cannot be equal to the letter at $$$P[i + (\frac{N}{2})]$$$.
This can be performed in $$$O(N \log N)$$$, due to sorting. However, due to the limited size of the alphabet, we can actually sort even faster using a non-comparative sorting algorithm such as counting sort.
Analysis — B. Birthday Cake
In what follows, let us suppose that the delicious part of the cake has $$$n$$$ rows and $$$m$$$ columns.
Test Set 1
When $$$\mathbf{K}=1$$$, we must consider two cases. If the delicious part is fully inside the cake, meaning that the outer cells are not delicious, then all grid lines around the delicious cells must be cut. Specifically, there are $$$n+1$$$ grid lines of length $$$m$$$ and $$$m+1$$$ grid lines of length $$$n$$$, so the answer is $$$n(m+1)+m(n+1)=2nm+n+m$$$ plus the minimum distance to cut from the border to the delicious part. On the other hand, if the delicious part shares some border with the whole cake, then the answer is $$$2nm+n+m$$$ minus the length of the shared border. The time complexity is $$$O(1)$$$.
Test Set 2
Let us start out simple. Suppose a cake of size $$$n \times m$$$ is entirely delicious and needs to be cut into $$$1 \times 1$$$ squares. This means that we need to cut the cake along all internal grid lines, which are marked bold in the following picture. Moreover, suppose for the moment that our knife is infinitely long. One way to cut the cake would be to make $$$n-1$$$ horizontal cuts and then make $$$m-1$$$ vertical cuts for each of the resulting $$$n$$$ horizontal strips. This strategy amounts to $$$n-1+n(m-1)=nm-1$$$ cuts. If we start with $$$m-1$$$ long vertical cuts first, then we would need $$$n-1$$$ horizontal cuts for each of the $$$m$$$ vertical strips, which again results in $$$m-1+m(n-1)=nm-1$$$ cuts.
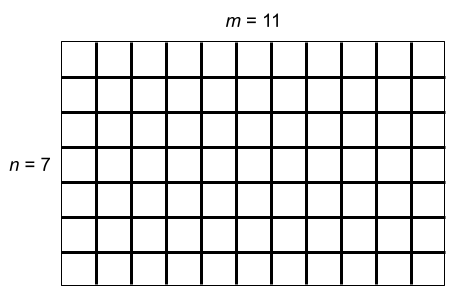
Can we do any better? No. In order to prove this claim, let us consider the worst case scenario where we make cuts of length $$$1$$$ only, which means $$$n(m-1)+m(n-1)=2nm-n-m$$$ cuts in total. Since we have a very long knife, we can try to combine or merge some of those unit cuts into longer cuts. Now, at each internal grid point, we can merge the two vertical cuts meeting at that point or the two horizontal cuts, but not both. Thus, we can save at most one cut at each internal grid point. There are $$$(n-1)(m-1)=nm-n-m+1$$$ internal grid points, which is how many cuts we can possibly save. It follows that we need at least $$$2nm-n-m-(nm-n-m+1)=nm-1$$$ cuts to divide the cake into unit squares.
Now that we know how to cut a fully delicious cake with a sufficiently long knife (i.e. $$$\mathbf{K} \ge n$$$ or $$$\mathbf{K} \ge m$$$), let us turn our attention to the case where the length of the knife is $$$\mathbf{K} \lt \min(n,m)$$$. With a cake this large, some cuts will necessarily terminate at a previously unexposed internal grid point. For convenience, we will call them red points. And if we continue the reasoning from the previous paragraph, the red points will not save a cut for us. In other words, as soon as we stop at a previously unexposed grid point, the three other grid lines meeting at that point will belong to different cuts with no chance of merging any two of them. Conversely, if a cut exposes an internal grid point without terminating at it, then that grid point belongs to just three different cuts and so one cut is saved. Consequently, we want to minimize the number of red points.
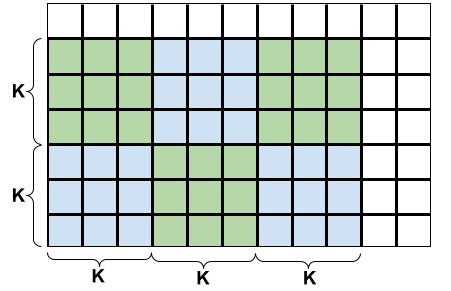
To prove a lower bound on the number of red points, let us consider $$$\lfloor \frac{n-1}{\mathbf{K}} \rfloor$$$ rows of $$$\mathbf{K} \times \mathbf{K}$$$ blocks, $$$\lfloor \frac{m-1}{\mathbf{K}} \rfloor$$$ blocks in each row as shown in the following picture for $$$\mathbf{K}=3$$$. If we consider the blocks open at the left and bottom sides and closed at the right and top sides, then each of the blocks contains $$$\mathbf{K} \times \mathbf{K}$$$ internal grid points and any two blocks are disjoint. One can easily verify that the very first cut that has a point common with a particular block will create a red point in that block. Since the blocks are disjoint, there will be at least $$$\lfloor \frac{n-1}{\mathbf{K}} \rfloor \times \lfloor \frac{m-1}{\mathbf{K}} \rfloor$$$ red points for any cutting strategy.
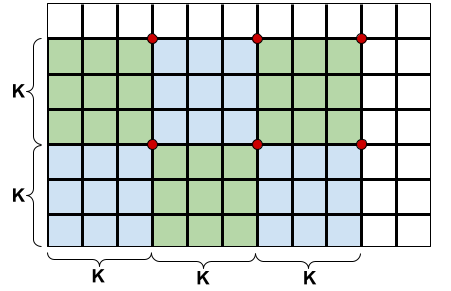
It turns out that for an optimal cutting strategy this is also the upper bound on the number of red points. One way of achieving this bound is to select the top-right corner of each block as the red point, cut out the blocks with $$$2\lfloor \frac{n-1}{\mathbf{K}} \rfloor \times \lfloor \frac{m-1}{\mathbf{K}} \rfloor$$$ full cuts, and finally cut all the blocks and the L-shaped remaining part into unit squares without ever terminating at a previously unexposed grid point (i.e. without introducing new red points). Recall that every internal grid point that is not red saves us one cut. It follows that the minimum number of cuts to partition a fully delicious cake is $$$nm-1+\lfloor \frac{n-1}{\mathbf{K}} \rfloor \times \lfloor \frac{m-1}{\mathbf{K}} \rfloor$$$. Note that the case with a sufficiently long knife is a special case of this formula, as $$$\lfloor \frac{n-1}{\mathbf{K}} \rfloor \times \lfloor \frac{m-1}{\mathbf{K}} \rfloor=0$$$.
It remains to solve the problem for a cake that is partially not delicious. Intuitively, it seems reasonable to cut out the delicious rectangle first and then proceed with the above strategy to partition the delicious part into unit squares. To cut out the delicious rectangle, we should start cutting from the outer border of the cake towards one of the corners of the delicious rectangle and then cut around the rectangle as shown in the following picture for $$$\mathbf{K}=3$$$. There are eight symmetric variants to try and we take the minimum number of cuts obtained this way. We should be careful, though, not to include any sides of the delicious rectangle that are touching the border of the whole cake.
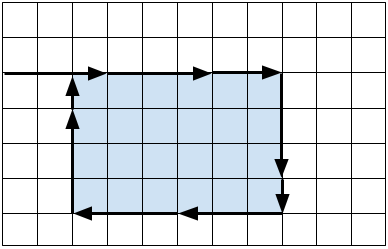
A skeptical reader might ask whether it could be worth considering a cutting strategy where we start from the outer border and cut towards somewhere in the middle of the delicious rectangle. If the distance from the border to the delicious rectangle is not divisible by $$$\mathbf{K}$$$, then the last step would cut right into the delicious part and perhaps save one cut for the internal grid lines of the delicious rectangle. It can be shown, however, that we would need one extra cut for the outline in this case, so overall we would not gain anything. The proof of this claim is technical yet not very interesting, so it is left for the reader as an exercise.
The time complexity of the solution for Test Set 2 is still $$$O(1)$$$.
Analysis — C. Palindromic Crossword
Test Set 1
Suppose we were solving the crossword on paper. Then, for each word we will check if any of the palindromic positions can be filled (we consider two positions as "palindromic positions" if their distances to the closer word boundary (start or end) are equal). We will need to repeat this process until no more positions in the crossword can be filled. We can simulate this process by repeatedly trying to fill in one more position. The simulation ends when we cannot fill any character in the crossword.
Runtime analysis: In each successful pass over the crossword, at least one
character will be filled. There are at most $$$\mathbf{N} \times \mathbf{M}$$$ spots on the
crossword that need to be filled, which means at most $$$\mathbf{N} \times \mathbf{M}$$$
passes are needed to fill the crossword. Now, in each pass over the crossword,
we will be checking all the rows and columns once. We will need to divide each
row/column into its constituent words (using '#' as separators). Then for each
word, we will check the palindromic positions for a filled character and fill-in
the other position. This process will take $$$O(\mathbf{N} \times \mathbf{M})$$$ for checking
all rows and columns once. So, total runtime will be:
$$$O((\mathbf{N} \times \mathbf{M}) \times (\mathbf{N} \times \mathbf{M})) = O(\mathbf{N}^2 \times \mathbf{M}^2)$$$
Test Set 2
Consider the following crossword:
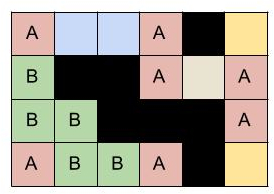
This image shows the equivalence classes on a partially solved crossword. Now, if
we find these equivalence classes, we can fill all the cells for each class if
any of the cells in that class contains a character.
Now, to build equivalence classes, let us start by building a graph from our
crossword. We will consider all cells in the crossword (which are not '#') as
nodes of our graph and draw edges between palindromic positions. To generate
these edges, we can traverse over all rows and then over all columns of the
crossword. For each row/column, split it into its constituent words and add an
edge between the palindromic positions. Now, if two cells belong to the same
connected component, they are equivalent. We can find connected components
(equivalence classes) optimally from our constructed graph using any
graph search algorithm (such as DFS or BFS) or using DSU.
Runtime analysis: Any graph traversal algorithm will visit each cell only once
and a cell can be connected to at most two other cells. Then, each cell will be
visited at most once more when filling in equivalence classes. So, total runtime
will be:
$$$O(\mathbf{N} \times \mathbf{M})$$$
Analysis — D. Increasing Sequence Card Game
Test Set 1
For the first test set, we can generate all possible arrangements of the cards from $$$1$$$ to $$$\mathbf{N}$$$. For each arrangement of the cards, we can play the game to find the score for that particular arrangement. Then the expected score of the game will be the average score over all arrangements. The total number of possible arrangements for $$$\mathbf{N}$$$ cards is $$$\mathbf{N}!$$$.
The time complexity is $$$O(\mathbf{N} \cdot \mathbf{N}!)$$$ which is under the required limit for $$$\mathbf{N} = 10$$$.
Test Set 2
Our previous strategy would not work for this test set.
Let us consider arrangements where the number on top of the pile is $$$x$$$.
Then among the remaining $$$\mathbf{N} - 1$$$ cards, all the cards that are smaller
than $$$x$$$ will be discarded. We only need to take care of the ones that are
greater than $$$x$$$. So, the expected score for arrangements with $$$x$$$ on
top of the pile will be one higher than the expected score of the rest of the
cards greater than $$$x$$$. Also, it does not matter what the starting and
ending number on the cards is, all that matters is the number of cards. So, the
expected score of cards from $$$x + 1$$$ to $$$\mathbf{N}$$$ is equal to expected score of
cards from $$$1$$$ to $$$\mathbf{N} - x$$$. Assuming $$$E_\mathbf{N}$$$ denotes the expected
score of $$$\mathbf{N}$$$ cards, the expected score when $$$x$$$ is on top is $$$E_{\mathbf{N} - x}
+ 1$$$.
Now, $$$x$$$ ranges from $$$1$$$ to $$$\mathbf{N}$$$, so the expected score for $$$\mathbf{N}$$$ cards is $$$E_\mathbf{N} = \frac{\sum_{x=1}^{\mathbf{N}}(E_{\mathbf{N} - x} + 1)}{\mathbf{N}} = \frac{\sum_{i=0}^{\mathbf{N}-1}E_{i}}{\mathbf{N}} + 1$$$. The summation in the term is a cumulative sum of expected scores of first $$$\mathbf{N}-1$$$ natural numbers. So, expected score for $$$\mathbf{N}$$$ cards can be computed in linear time if we maintain the cumulative sum of the expected score for $$$\mathbf{N}-1$$$ cards.
Test Set 3
Let us denote $$$\sum_{i=0}^{\mathbf{N}}E_i$$$ as $$$S_\mathbf{N}$$$, then from the result of
the previous section, we have $$$E_\mathbf{N} = \frac{S_{\mathbf{N}-1}}{\mathbf{N}} + 1$$$. Now, for
$$$E_{\mathbf{N}+1}$$$ we have:
$$$E_{\mathbf{N}+1} = \frac{S_\mathbf{N}}{\mathbf{N}+1} + 1 = \frac{E_\mathbf{N} + S_{\mathbf{N}-1}}{\mathbf{N}+1} + 1$$$
Now, substituting $$$E_\mathbf{N}$$$ from the previous result, we get:
$$$E_{\mathbf{N}+1} = \frac{\frac{S_{\mathbf{N}-1}}{\mathbf{N}} + 1 + S_{\mathbf{N}-1}}{\mathbf{N}+1} + 1 =
\frac{\frac{(\mathbf{N}+1)S_{\mathbf{N}-1}}{\mathbf{N}} + 1}{\mathbf{N}+1} + 1$$$
$$$\Rightarrow E_{\mathbf{N}+1} = \frac{S_{\mathbf{N}-1}}{\mathbf{N}} + \frac{1}{\mathbf{N}+1} + 1$$$
$$$\Rightarrow E_{\mathbf{N}+1} = E_\mathbf{N} + \frac{1}{\mathbf{N}+1}$$$
This is the
harmonic series
since $$$E_1 = 1$$$. We can estimate $$$E_\mathbf{N}$$$ for $$$\mathbf{N} \gt 10^{6}$$$
with $$$E_{10^{6}} + \int_{10^{6} +1}^{\mathbf{N}+1} \frac{1}{x} \,dx$$$. Since
$$$\int \frac{1}{x} \,dx = \log(x) + C$$$, we get (for $$$\mathbf{N} \gt 10^6$$$):
$$$E_\mathbf{N} = E_{10^{6}} + \log(\mathbf{N}+1) - \log(10^{6} + 1)$$$.
We can precompute the harmonic series till $$$10^6$$$ in linear time and then estimate the score using the above formula for $$$\mathbf{N} \gt 10^6$$$. So, the overall time complexity is constant, specifically $$$O(10^6)$$$ for the precomputation.
Error Bounds
Consider the following $$$3$$$ graphs:
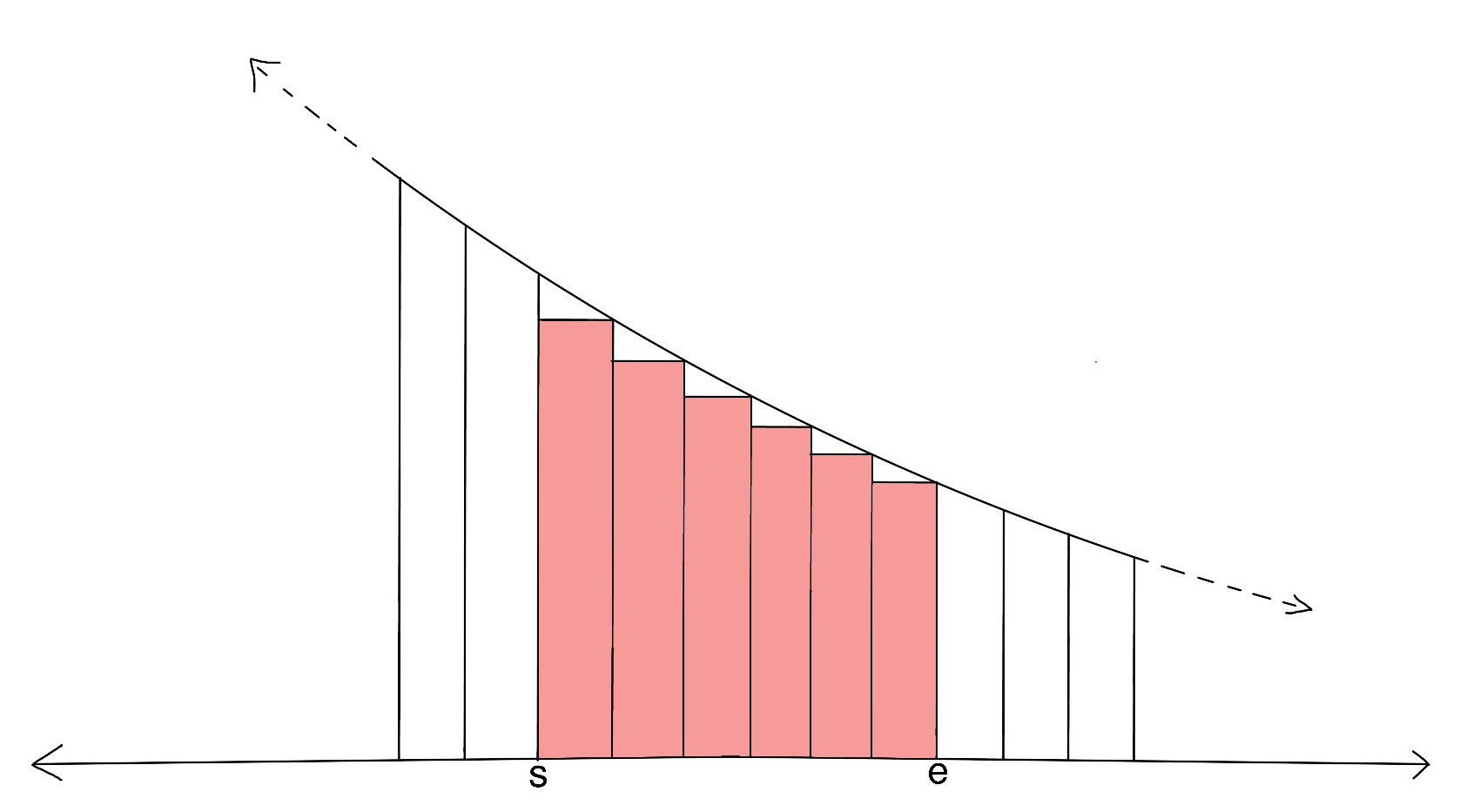
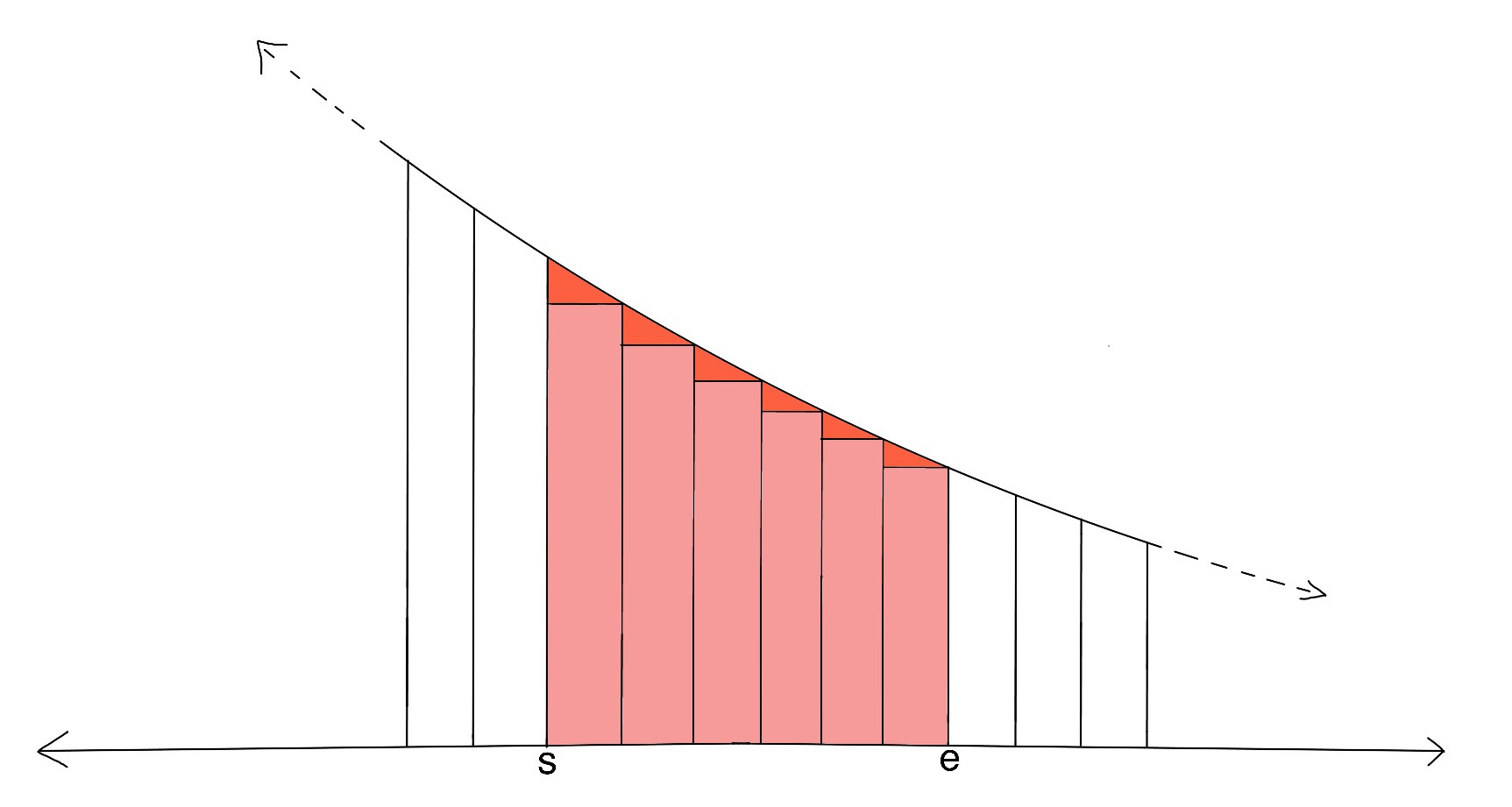
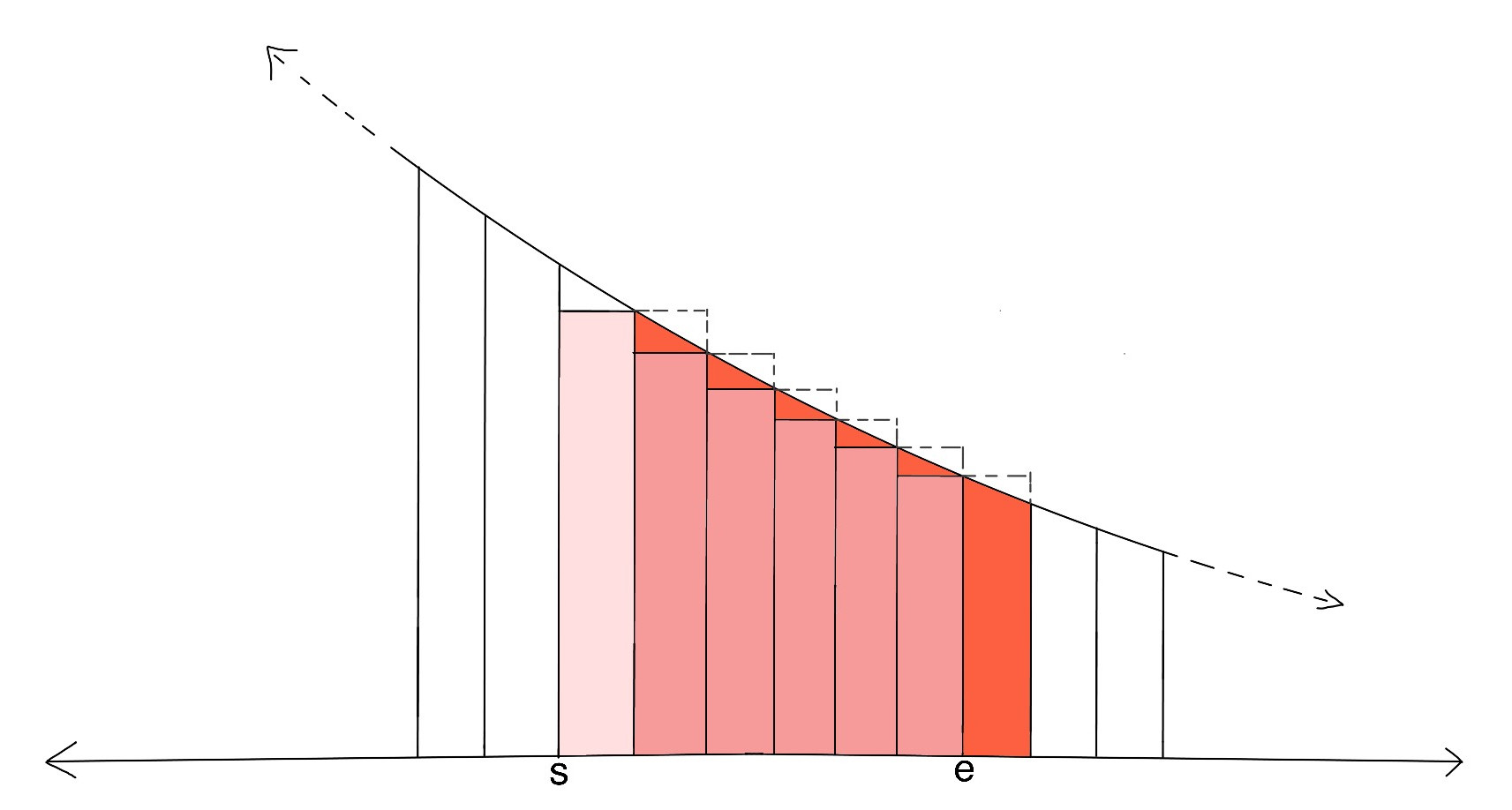
The first image represents the actual number we need $$$\sum_{x=s+1}^{e}\frac{1}{x}$$$, second image represents a larger area $$$\int_{s}^{e}\frac{1}{x}\,dx$$$ and third image represents a smaller area $$$\int_{s+1}^{e+1}\frac{1}{x}\,dx$$$. So, error (denoted as $$$Er_{s,e}$$$) is given by:
$$$Er_{s,e} \lt \int_{s}^{e}\frac{1}{x}\,dx -
\int_{s+1}^{e+1}\frac{1}{x}\,dx$$$
$$$\Rightarrow Er_{s,e} \lt \int_{s}^{s+1}\frac{1}{x}\,dx -
\int_{e}^{e+1}\frac{1}{x}\,dx \lt \int_{s}^{s+1}\frac{1}{x}\,dx$$$
$$$\Rightarrow Er_{s,e} \lt \frac{1}{s}$$$
Now, we are estimating only after $$$10^6$$$, so $$$s = 10^6$$$, hence
$$$Er_{10^6,e} \lt 10^{-6}$$$.