Google Kick Start Archive — Round D 2021 problems

The integers $$$A, B$$$ and $$$C$$$ are in an arithmetic progression if $$$B - A = C - B$$$ , that is, $$$A + C = 2 \times B$$$ . As $$$B$$$ is an integer, $$$\frac{(A + C)}{2}$$$ must also be an integer, which means $$$A + C$$$ must be an even integer. We will use this condition to find the solution to the problem.

In a $$$3 \times 3$$$ grid of integers, there are $$$8$$$ sequences which can be an arithmetic progression.

1. $$$\mathbf{G_{0,0}}, \mathbf{G_{0,1}}, \mathbf{G_{0,2}}$$$
2. $$$\mathbf{G_{0,0}}, \mathbf{G_{1,0}}, \mathbf{G_{2,1}}$$$
3. $$$\mathbf{G_{2,0}}, \mathbf{G_{2,1}}, \mathbf{G_{2,2}}$$$
4. $$$\mathbf{G_{0,2}}, \mathbf{G_{1,2}}, \mathbf{G_{2,2}}$$$
5. $$$\mathbf{G_{1,0}}, G_{1,1}, \mathbf{G_{1,2}}$$$
6. $$$\mathbf{G_{0,1}}, G_{1,1}, \mathbf{G_{2,1}}$$$
7. $$$\mathbf{G_{0,2}}, G_{1,1}, \mathbf{G_{2,0}}$$$
8. $$$\mathbf{G_{0,0}}, G_{1,1}, \mathbf{G_{2,2}}$$$

We want to find, at max, how many of the above sequences can be arithmetic sequences at the same time.

Test Set 1

The first four sequences do not contain the missing value, and for each such sequence we can find if they form an arithmetic sequence in $$$O(1)$$$ using the above condition that if $$$A, B$$$ and $$$C$$$ form an arithmetic progression then $$$A + C = 2 \times B$$$. Now for the remaining four sequences, we iterate over all values from $$$-50$$$ to $$$50$$$ and assign it to the missing value $$$G_{1,1}$$$ and check how many of the remaining four form arithmetic progressions. The maximum number of sequences that can be created for a value as we iterate gives us the number of arithmetic progressions in the last four sequences.

Complexity : $$$O(max(\mathbf{G_{i,j}}))$$$ per test case

Test Set 2

The first four sequences do not contain the missing value and for each one of them we can check if they form an arithmetic progression using the condition described above. For the remaining sequences, we cannot iterate over all values from $$$-1000000000$$$ to $$$1000000000$$$ as it will result in a TLE. We will use the fact that if $$$A, B$$$ and $$$C$$$ form an arithmetic progression for given values of $$$A$$$ and $$$C$$$ then there will be exactly one $$$B$$$ which will exist if and only if $$$A + C$$$ is an even integer and $$$B$$$ will be equal to $$$\frac{(A + C)}{2}$$$. For each of the last four sequences, consider $$$G_{1,1}$$$ as $$$B$$$ and the values in the other two squares as $$$A$$$ and $$$C$$$. For the sequences where $$$A + C$$$ is even, evaluate $$$B = \frac{(A + C)}{2}$$$ and find the maximum number of sequences which evaluate to the same B. If we consider such a $$$B$$$ as $$$G_{1,1}$$$, the number of arithmetic progressions in the last four sequences will be maximised.

Complexity : $$$O(1)$$$ per test case

We are given $$$\mathbf{N}$$$ intervals and are asked to find the maximum number of intervals we can obtain if we perform a maximum of $$$\mathbf{C}$$$ cuts. There are a few key observations required to solve this problem.

First, performing a cut at the same point $$$X$$$ more than once will not result in any additional intervals. After the initial cut, all intervals which contained $$$X$$$ will now be split into intervals that have $$$X$$$ as an endpoint, and thus cannot be cut further at $$$X$$$.

Second, a cut at $$$X$$$ will result in the same number of additional intervals regardless of the number of cuts performed earlier at other points. This implies that at most $$$N$$$ additional intervals can be obtained with each cut.

Based on the aforementioned observations, we can solve this problem as follows. Let $$$A_{j}$$$ represent the number of points at which performing a cut will result in $$$j$$$ additional intervals ($$$0 \le j \le \mathbf{N}$$$). Iterating over $$$A$$$ in reverse order, we perform the cuts greedily, adding $$$j \cdot \min(A_{j}, \mathbf{C})$$$ to our result, and decrementing $$$\mathbf{C}$$$ by $$$\min(A_{j}, \mathbf{C})$$$ until $$$\mathbf{C} = 0$$$. The final answer is the result.

Iterating over $$$A$$$ can be done in $$$O(\mathbf{N})$$$. Now, we will go over how to populate $$$A$$$ for the two test sets.

Test set 1

For this test set, we can iterate over each point coordinate and count the number of intervals it lies strictly within, i.e. for each $$$X \in [\min(\mathbf{L_i}),\max(\mathbf{R_i})]$$$, we count the number of intervals such that $$$\mathbf{L_i} \lt X \lt \mathbf{R_i}$$$. Let that number be $$$k$$$. Then, we increment $$$A_k$$$.

This can be performed in $$$O(\mathbf{N} \cdot \max(\mathbf{R_i}))$$$.

Test set 2

For this test set, the above solution would exceed the time limits.

We observe that the number of additional intervals obtained by a cut at two consecutive points $$$X$$$ and $$$X+1$$$ are the same, except, possibly, when some intervals start or end at these points. We can construct a sorted map $$$M_X$$$ which maps the coordinate $$$X$$$ to the number of additional intervals it lies within as compared to $$$X-1$$$. That is, for each starting interval endpoint $$$\mathbf{L_i}$$$, we increment $$$M_{\mathbf{L_i}+1}$$$. And for each ending interval endpoint $$$\mathbf{R_i}$$$, we decrement $$$M_{\mathbf{R_i}}$$$.

Consider an example with the following intervals: $$$[3, 7], [1, 5], [4, 7]$$$. The mappings created are $$$M_2 = 1, M_4 = 1, M_5 = 0$$$, and $$$M_7 = -2$$$: because one interval begins at 1 ($$$M_2$$$ += $$$1$$$), one interval begins at 3 ($$$M_4$$$ += $$$1$$$), one interval begins at 4 ($$$M_5$$$ += $$$1$$$), one intervals ends at 5 ($$$M_5$$$ -= $$$1$$$) and two intervals end at 7 ($$$M_7$$$ -= $$$2$$$).

Finally, we iterate over the map in sorted order of keys, keeping track of the number of overlapping intervals $$$j$$$, the previous key $$$k_{prev}$$$, and the current key $$$k_{curr}$$$. We increment $$$A_j$$$ by $$$k_{curr} - k_{prev}$$$. Now $$$A_j$$$ can be used to compute the final solution as described above.

In the above example, we iterate over the keys of $$$M$$$, and start with $$$j = 0$$$. All points smaller than the first key (2) will produce zero additional intervals.
We increment $$$j$$$ by $$$M_2$$$ and go to the next key. Now $$$j = 1, k_{curr} = 4, k_{prev} = 2$$$. We increment $$$A_j = A_1$$$ by $$$k_{curr} - k_{prev} = 2$$$, because the 2 points (2, 3) will produce 1 additional interval if we perform a cut on them.
Now we increment $$$j$$$ by $$$M_4$$$ and go to the next key. Now $$$j = 2, k_{curr} = 5, k_{prev} = 4$$$. We increment $$$A_2$$$ by 1, because there is 1 point (4) at which performing cuts will result in 2 additional intervals.
Then, we increment $$$j$$$ by $$$M_5 = 0$$$ and go to the next key, so $$$j = 2, k_{curr} = 7, k_{prev} = 5$$$. Again we increment $$$A_2$$$ by 2, because the points 5, 6 also result in 2 additional intervals.
Finally we increment $$$j$$$ by $$$M_7 = -2$$$ and end.
The final result is $$$A_1 = 2, A_2 = 3$$$, and we can start performing greedy cuts.

Constructing the map requires adding $$$2 \cdot \mathbf{N}$$$ endpoints to it, with each addition requiring $$$O(\log(\mathbf{N}))$$$. Therefore, the overall time complexity is $$$O(\mathbf{N} \cdot \log(\mathbf{N}))$$$.

Test set 1

For consistency, we will use $$$maxDifficulty$$$ to represent the maximum difficulty of a problem which is equal to $$$1000$$$ for this test set. As the difficulty of any problem can be at most $$$1000$$$, we can keep track of all the problems that can be used to test the students. This can be done by maintaining a boolean array $$$problemAvailable$$$ of size $$$maxDifficulty$$$ where $$$problemAvailable[i]$$$ is true if a problem is still available for difficulty $$$i$$$. We can iterate over the given $$$\mathbf{N}$$$ sets of problems and for each set $$$i$$$, mark that a problem exists for each difficulty $$$x$$$ such that $$$\mathbf{A_i} \le x \le \mathbf{B_i}$$$. As no two sets contain the problems with same difficulty level, we will iterate over a particular difficulty level at most once. Hence, we can fill the boolean array $$$problemAvailable$$$ in $$$O(maxDifficulty)$$$ time.

For each query $$$j$$$, we can iterate through all remaining problems and find out which problem has the difficulty $$$d$$$ such that $$$abs(d-\mathbf{S_j})$$$ is minimum. This can be done in $$$O(maxDifficulty)$$$ time. After finding such problem, we can remove this problem from the remaining problems by marking $$$problemAvailable[d]$$$ as false. This can be done in constant time. Hence, we can answer each query in $$$O(maxDifficulty)$$$ time. The overall complexity of the solution is $$$O(\mathbf{M} \times maxDifficulty)$$$.

Test set 2

We cannot list problems with all possible difficulties as maximum difficulty can go upto $$$10^{18}$$$ in this test set. As the problem sets contain problems with disjoint difficulties, we can store the problem sets as a range. This can be done by using a map where key denotes the starting value of the range of difficulty and value denotes the ending range of difficulty. To store the ranges from the initial problem sets, we would need insertion operation in map. Hence, we can store the ranges in $$$O(\mathbf{N} \times \log \mathbf{N})$$$ time complexity initially.

For a query $$$j$$$, we need to lookup into the map to find the problem with difficulty $$$d$$$ such that $$$abs(d-\mathbf{S_j})$$$ is minimized. We can perform an upper bound operation on map. In C++, one can use std::map::upper_bound method. upper_bound($$$z$$$) returns first element greater than $$$z$$$. Suppose upper_bound($$$\mathbf{S_j}$$$) returned $$$k$$$-th element of the map. There are several cases that could occur:

• $$$k=1.$$$
  
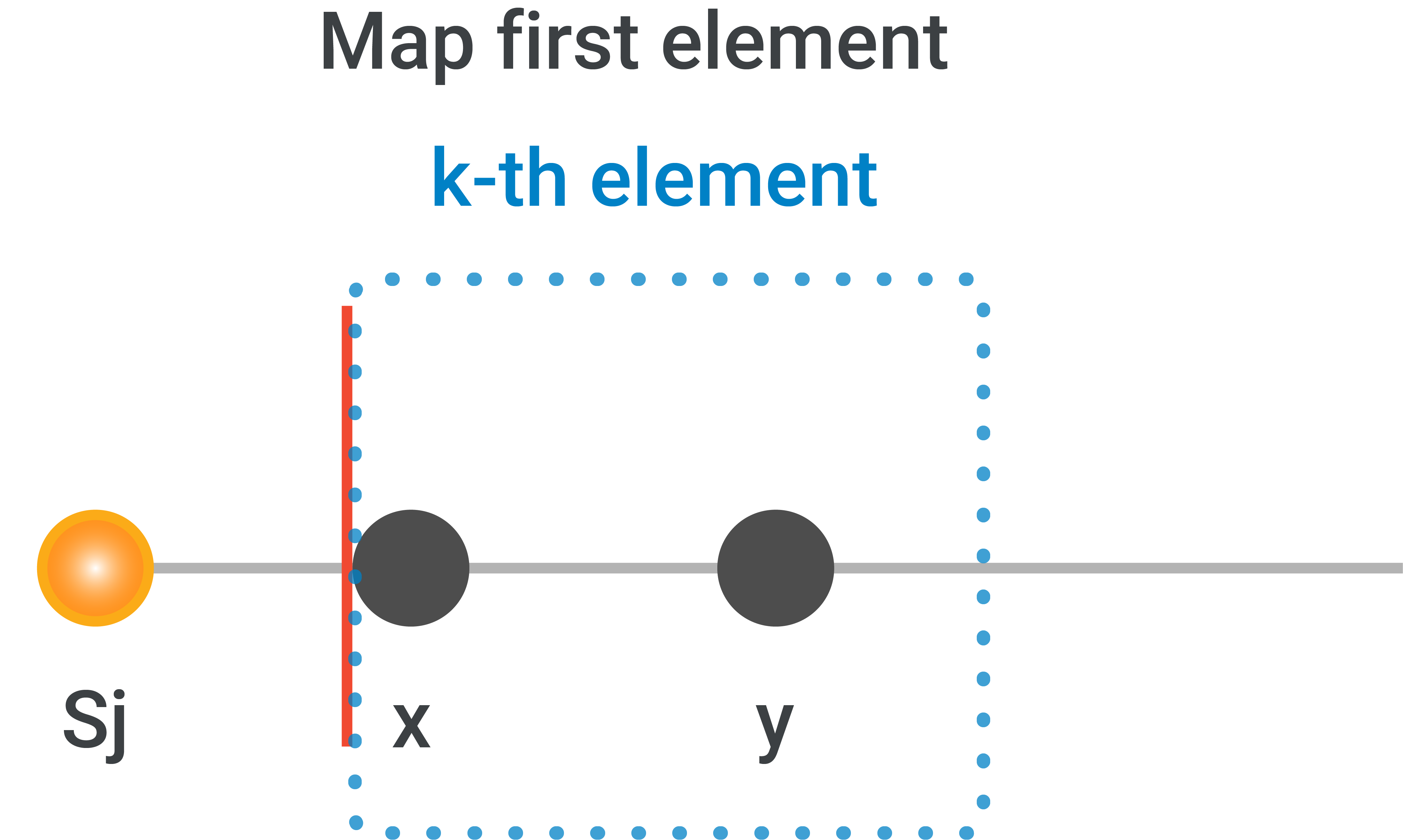
  This means that there is no range in map which could contain $$$\mathbf{S_j}$$$ as the first range in map contains all values greater than $$$\mathbf{S_j}$$$. Let the range corresponding to first entry by $$$(x,y)$$$. The problem with difficulty $$$x$$$ will be the one with closest value to $$$\mathbf{S_j}$$$. Thus, we can choose problem with difficulty $$$x$$$ for this query. We can now update this range to $$$(x+1,y)$$$ as problem with difficulty $$$x$$$ is not available anymore. If $$$x+1 \gt y$$$, we can remove this range.
• Let the range corresponding to $$$(k-1)$$$-th element in map be $$$(l,r)$$$. There are two cases here:
  • $$$l \le \mathbf{S_j} \le r$$$.
    
    This means that the problem with difficulty $$$\mathbf{S_j}$$$ exists. The answer to this query would be the problem with difficulty $$$\mathbf{S_j}$$$. As this problem is not available for the remaining queries, we can remove the range $$$(l,r)$$$ and insert 2 separate ranges $$$(l,\mathbf{S_j}-1)$$$ and $$$(\mathbf{S_j}+1, r)$$$. If any of the ranges is invalid, we can ignore that range.
  • $$$r \lt \mathbf{S_j}$$$.
    
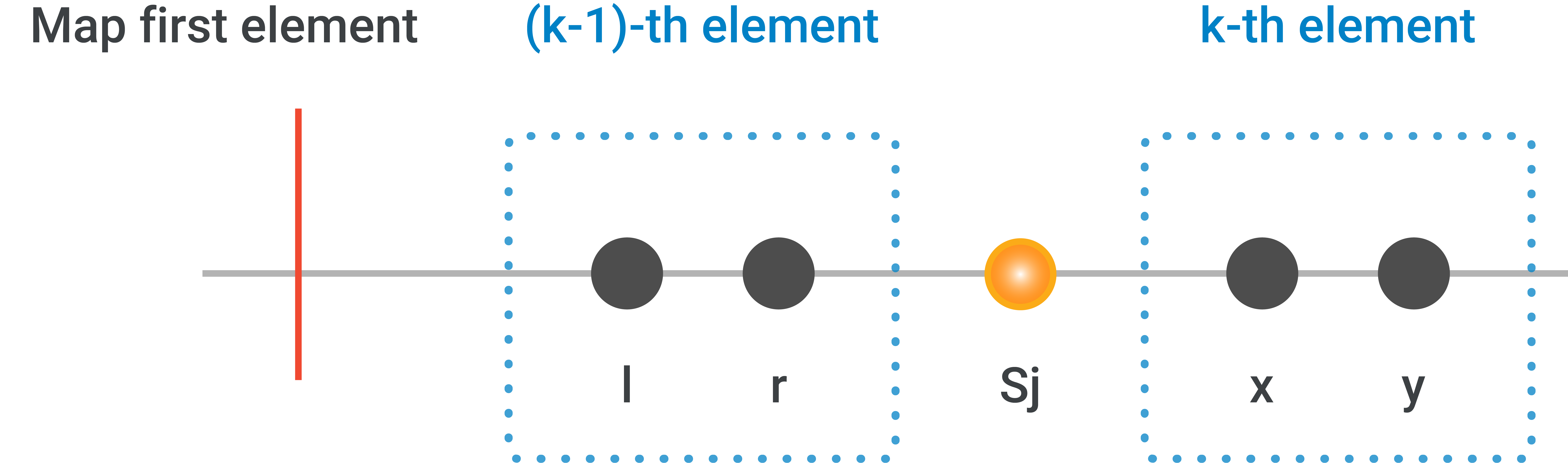
    This means that there is no problem with difficulty $$$\mathbf{S_j}$$$. If $$$\mathbf{S_j} - r \le x - \mathbf{S_j}$$$, then we can select the problem with difficulty $$$r$$$ as it is closest to $$$\mathbf{S_j}$$$. We can update the range $$$(l,r)$$$ to $$$(l,r-1)$$$ if it is a valid range. Otherwise, we can select the problem with difficulty $$$x$$$. We can update the range $$$(x,y)$$$ to $$$(x+1,y)$$$ if it is a valid range.

Each query can lead to addition of at most $$$1$$$ new entry into the map. Hence, the size of the map would be $$$O(\mathbf{N} + \mathbf{M})$$$. We perform $$$O(1)$$$ operations each of which takes $$$O(\log (\mathbf{N} + \mathbf{M}))$$$ time to compute answer for a single query. So, we can answer $$$\mathbf{M}$$$ queries in $$$O(\mathbf{M} \times \log (\mathbf{N} + \mathbf{M}))$$$ time. Hence, the overall complexity of the solution is $$$O(\mathbf{N} \times \log \mathbf{N} + \mathbf{M} \times \log (\mathbf{N} + \mathbf{M}))$$$.

Let us define $$$F(a, s) = V(a^{s} - (a \enspace mod \enspace \mathbf{P})^{s})$$$.
The main idea is to use segment trees as there are range queries and point updates. If we can calculate the $$$F(\mathbf{A_i}, \mathbf{S})$$$ efficiently, then we can query the range sum and also update the values using segment tree operations. Calculating the $$$F(a, s)$$$ part needs different approaches for different test sets.

Test Set 1

As $$$\mathbf{S}$$$ can only be at most 4, we can maintain individual segment trees for each $$$\mathbf{S}$$$. So now $$$\mathbf{S}$$$ is fixed for a single segment tree. The values of $$$\mathbf{A_i}$$$s are also small, so we can calculate $$$\mathbf{A_i}^{\mathbf{S}}$$$ without overflowing. Let us say we have 2 segment tree operations, $$$sum(start, end)$$$ which gives us the sum from index start to end and $$$update(idx, val)$$$ which updates the index $$$idx$$$ with val. We are maintaining maxS different segment trees. So initially in the j'th tree, we have the values $$$F(\mathbf{A_i}, \mathbf{j})$$$s. When there is a query like $$$\mathbf{2}$$$ $$$\mathbf{S}$$$ $$$\mathbf{L}$$$ $$$\mathbf{R}$$$, we call $$$sum(\mathbf{L}, \mathbf{R})$$$ on the $$$\mathbf{S}$$$th tree. And when there is an update like $$$\mathbf{1}$$$ $$$\mathbf{pos}$$$ $$$\mathbf{val}$$$, we have to update each tree, so we call $$$update(\mathbf{pos}, F(\mathbf{val}, j))$$$ on the j'th tree.

Building the trees initially takes $$$O(maxS \cdot \mathbf{N})$$$.
Type 1 query (update) takes $$$O(\mathbf{S} \cdot \log{\mathbf{N}})$$$.
Type 2 query takes $$$O(\log{\mathbf{N}})$$$.
The time complexity of this solution is $$$O(maxS \cdot \mathbf{N} + \mathbf{Q} \cdot \mathbf{S} \cdot \log{\mathbf{N}})$$$.

Test Set 2

As $$$\mathbf{S}$$$ and $$$\mathbf{A_i}$$$s are huge now, we can't maintain a segment tree for each $$$\mathbf{S}$$$ and also can't calculate $$$\mathbf{A_i}^{\mathbf{S}}$$$ without overflowing. So a different approach is needed.

The idea originates from lifting-the-exponent-lemma. The lemma states that, if P is a prime, and P divides a-b but divides neither a nor b, then $$$V(a^{n} - b^{n}) = V(a-b) + V(n)$$$. But it has a special case.
When $$$P = 2$$$ and n is even, then $$$V(a^{n} - b^{n}) = V(a-b) + V(a+b) + V(n) - 1$$$.
Here $$$V(x)$$$ carries the same meaning as defined in the problem statement.
Another observation is $$$\mathbf{A_i} - (\mathbf{A_i} \enspace mod \enspace \mathbf{P})$$$ is always divisible by $$$\mathbf{P}$$$, which makes it possible for us to use the lemma.

We will handle everything in $$$2$$$ cases.

Case 1 - $$$\mathbf{A_i}$$$ or $$$\mathbf{val}$$$ is divisible by $$$\mathbf{P}$$$:
We will have a segment tree for this. Initially we will update the indices having $$$\mathbf{A_i}$$$s divisible by $$$\mathbf{P}$$$ with $$$V(\mathbf{A_i})$$$s. When there is an update like $$$\mathbf{1}$$$ $$$\mathbf{pos}$$$ $$$\mathbf{val}$$$, we will update index $$$\mathbf{pos}$$$ with $$$V(\mathbf{val})$$$.
When we have a query like $$$\mathbf{2}$$$ $$$\mathbf{S}$$$ $$$\mathbf{L}$$$ $$$\mathbf{R}$$$, we will call $$$sum(\mathbf{L}, \mathbf{R})$$$ and multiply that with $$$\mathbf{S}$$$, because $$$F(\mathbf{A_i}, \mathbf{S}) = \mathbf{S} \cdot V(\mathbf{A_i})$$$ in this case.

Case 2 - $$$\mathbf{A_i}$$$ or $$$\mathbf{val}$$$ is not divisible by $$$\mathbf{P}$$$:
This has 2 subcases because of the special case, so we will have 2 separate segment trees. Initially we will update the indices having $$$\mathbf{A_i}$$$s not divisible by $$$\mathbf{P}$$$ with $$$V(\mathbf{A_i} - (\mathbf{A_i} \enspace mod \enspace \mathbf{P}))$$$ in one tree and with $$$V(\mathbf{A_i} + (\mathbf{A_i} \enspace mod \enspace \mathbf{P})) - 1$$$ in the other. When there is an update like $$$\mathbf{1}$$$ $$$\mathbf{pos}$$$ $$$\mathbf{val}$$$, we will update index $$$\mathbf{pos}$$$ with $$$V(\mathbf{val} - (\mathbf{val} \enspace mod \enspace \mathbf{P})) $$$ in the first tree and with $$$V(\mathbf{val} + (\mathbf{val} \enspace mod \enspace \mathbf{P})) - 1$$$ on the other .
We will also maintain another segment tree that will help us query the number of values that are not divisible by $$$\mathbf{P}$$$ in a given range.
When we have a query like $$$\mathbf{2}$$$ $$$\mathbf{S}$$$ $$$\mathbf{L}$$$ $$$\mathbf{R}$$$, if $$$\mathbf{P} = 2$$$ and $$$\mathbf{S}$$$ is even, then we call $$$sum(\mathbf{L}, \mathbf{R})$$$ on both segment trees and add them. Otherwise we call it only on the first one. Also if there are X values not divisible by $$$\mathbf{P}$$$ in the range $$$\mathbf{L}$$$ to $$$\mathbf{R}$$$, we will add $$$X \cdot V(\mathbf{S})$$$ to the answer.

The final answer is the summation of the queries from the 2 above cases.

$$$V(\mathbf{S})$$$ can be calculated in $$$O(\log\mathbf{S})$$$. And when $$$\mathbf{A_i}$$$ is divisible by $$$\mathbf{P}$$$, the value of $$$V(\mathbf{A_i}^{\mathbf{S}} - (\mathbf{A_i} \enspace mod \enspace \mathbf{P})^{\mathbf{S}})$$$ is just $$$V(\mathbf{A_i}^{\mathbf{S}})$$$, which is $$$\mathbf{S} \cdot V(\mathbf{A_i})$$$, that can be calculated with brute force with complexity of $$$O(\log\mathbf{A_i})$$$.

The time complexity of this solution is $$$O(\mathbf{N}\log(\max(\mathbf{A_i})) + \mathbf{Q} \cdot (\log\mathbf{N} + \log(\max(\mathbf{S}, \mathbf{val}))))$$$.