Google Kick Start Archive — Round H 2020 problems
Overview
Thank you for participating in Kick Start 2020 Round H.
Cast
Retype: Written by Sudarsan Srinivasan and prepared by Swapnil Gupta.
Boring Numbers: Written by Saurabh Joshi and prepared by Shantam Agarwal.
Rugby: Written by Krists Boitmanis and prepared by Swapnil Gupta.
Friends: Written by Ian Tullis and prepared by Mohamed Yosri Ahmed.
Solutions, other problem preparation, reviews and contest monitoring by Anson Ho, Anushi Maheshwari, Bartosz Kostka, Bohdan Pryshchenko, Cristhian Bonilha, Devanshu Agarwal, Diksha Saxena, Ian Tullis, Jared Gillespie, Kashish Bansal, Krists Boitmanis, Lalit Kundu, Lizzie Sapiro, Marcin Wawerka, Michał Łowicki, Mohamed Yosri Ahmed, Muntakim Sadik, Ruoyu Zhang, Sadia Atique, Sai Surya Upadrasta, Saurabh Joshi, Saurabh Nijhara, Shantam Agarwal, Sherry Wu, Shweta Karwa, Sudarsan Srinivasan, Swapnil Gupta, Teja Vardhan Reddy Dasannagari, Vikash Dubey, and Vipin Singh.
Analysis authors:
- Retype: Swapnil Gupta
- Boring Numbers: Devanshu Agarwal
- Rugby: Cristhian Bonilha
- Friends: Krists Boitmanis
A. Retype
Problem
After spending many hours studying for programming competitions, you decided to take a rest and play video games. You are currently playing an adventure game called Quick Start.
This game has N levels, and you are currently on the K-th level. Unfortunately, you just realized that to beat the boss at the final level, you will need a special sword, which can be picked up at level S. You have already completed that level, but you forgot to pick up the sword at that level.
Now you want to pick up the sword and finish the game in the least amount of time possible, and for that you have two options:
- Restart the game and complete all levels again, starting from level 1.
- Move to previous levels until you reach level S, pick up the sword and complete all the remaining levels, starting from level S.
Every time you enter a level you have to exit it, either by completing it and going to the next level or by moving to a previous level or by finishing / exiting the game. Exiting any level takes 1 minute. That means, for example, that it took you L minutes to complete the first L levels.
Your task is to discover which option would result in the least amount of total time to finish the game (including the time you have already spent).
Input
The first line of the input gives the number of test cases, T. T test cases follow.
The first (and only) line of each test case contains three integers N, K and S: the number of levels in the game, the current level you are in, and the level where you have to pick up the sword, respectively.
Output
For each test case, output one line containing Case #x: y, where x
is the test case number (starting from 1) and y is the least amount of total
time to finish the game.
Limits
Time limit: 20 seconds.
Memory limit: 1 GB.
1 ≤ T ≤ 100.
1 ≤ S < K < N.
Test Set 1
N ≤ 1000.
Test Set 2
N ≤ 109.
Sample
2 10 5 2 10 7 6
Case #1: 15 Case #2: 12
In Sample Case #1, it took you 4 minutes to complete the first 4 levels and enter 5-th level. Restarting the game and completing all levels again would take 11 more minutes (1 minute to restart and 10 to complete 10 levels), which adds up to 15 minutes. The other option would be to move backwards until you reach level 2 (which would take 3 minutes), and then complete all the remaining levels (taking 9 more minutes), which would result in a total of 16 minutes.
In Sample Case #2, it took you 6 minutes to complete the first 6 levels and enter 7-th level. Moving backwards until reaching level 6 (one minute), and then completing all the remaining levels (5 minutes), would take a total of 12 minutes to finish the game.
B. Boring Numbers
Problem
Ron read a book about boring numbers. According to the book, a positive number is called boring if all of the digits at even positions in the number are even and all of the digits at odd positions are odd. The digits are enumerated from left to right starting from 1. For example, the number 1478 is boring as the odd positions include the digits {1, 7} which are odd and even positions include the digits {4, 8} which are even.
Given two numbers L and R, Ron wants to count how many numbers in the range [L, R] (L and R inclusive) are boring. Ron is unable to solve the problem, hence he needs your help.Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case consists of a single line with two numbers L and R.
Output
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is the count of boring numbers.
Limits
Time limit: 20 seconds.
Memory limit: 1 GB.
1 ≤ T ≤ 100.
Test Set 1
1 ≤ L ≤ R ≤ 103.
Test Set 2
1 ≤ L ≤ R ≤ 1018.
Sample
3 5 15 120 125 779 783
Case #1: 6 Case #2: 3 Case #3: 2
In Sample Case #1, the numbers in the range are {5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15} out of which {5, 7, 9, 10, 12, 14} are boring, hence the answer is 6.
In Sample Case #2, the numbers in the range are {120, 121, 122, 123, 124, 125} out of which {121, 123, 125} are boring, hence the answer is 3.
In Sample Case #3, the numbers in the range are {779, 780, 781, 782, 783} out of which {781, 783} are boring, hence the answer is 2.
C. Rugby
Problem
On a far away planet, rugby is played in the two dimensional Cartesian coordinate system without bounds. The players can occupy integer grid points only and they can move to the neighboring grid points in any of the four cardinal directions. Specifically, if a player is currently at the point (X, Y), then they can move to either of the points (X+1, Y), (X-1, Y), (X, Y+1), or (X, Y-1) in a single step.
After the game, N players are scattered throughout the coordinate system such that any grid point is empty or occupied by one or more players. They want to gather for a picture and form a perfect horizontal line of N grid points, one player per point, all occupied points next to each other. Formally, the players have to move so as to occupy the grid points (X, Y), (X+1, Y), (X+2, Y), ..., (X+N-1, Y) for some coordinates X and Y. What is the minimum total number of steps the players should make to form a perfect line if they are free to choose the position of the line in the coordinate system and the ordering of players is not important?
Input
The first line of the input gives the number of test cases T. T test cases follow. The first line of each test case gives the number of players N. The subsequent N lines give the initial coordinates of the players. The i-th of these lines contains two integers Xi and Yi, which describe the initial position of i-th player (1 ≤ i ≤ N).
Output
For each test case, output one line containing Case #x: y, where x is
the test case number (starting from 1) and y is the minimum total number of steps
that the players need to make in order to form a perfect horizontal line.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 100.
Test Set 1
Time limit: 20 seconds.
1 ≤ N ≤ 10.
-500 ≤ Xi ≤ 500.
-500 ≤ Yi ≤ 500.
Test Set 2
Time limit: 40 seconds.
1 ≤ N ≤ 105 for at most 10 cases.
1 ≤ N ≤ 104 for the remaining cases.
-109 ≤ Xi ≤ 109.
-109 ≤ Yi ≤ 109.
Sample
2 2 1 1 4 4 3 1 1 1 2 1 3
Case #1: 5 Case #2: 4
In the first test case, one of many optimal solutions is obtained by the second player moving two steps to the left and three steps down to the point (2, 1).
In the second test case, a perfect line can be formed with a total of four steps if the first player moves to the point (0, 2) and the third player moves to the point (2, 2).
D. Friends
Problem
There are N people in the world numbered 1 to N. The i-th person has a distinct name Si that is a string of uppercase English letters.
Two people are friends if and only if there is some letter that appears at least once in each of their names. Any such letter does not need to be at the same position in both names. After all, friendship requires having something in common!
A friendship chain of length n between person A and person B is a sequence of people X1, X2, ..., Xn such that X1 = A, Xn = B, and Xi and Xi+1 are friends, for i=1 to n-1. Note that any two people can have zero or more friendship chains between them.
For each of the given Q pairs of people, can you find the length of the shortest friendship
chain between them? If there is no friendship chain between a pair, output -1.
Input
The first line of the input gives the number of test cases, T. T test cases follow. The first line of each test case contains the two integers N and Q. The second line contains N strings, which are people's names. The i-th string (starting from 1) is Si. Then, Q lines follow, describing the queries. The i-th of these lines contains the two integers Xi and Yi, which are the indexes (counting starting from 1) of a pair of people in the list of names.
Output
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y
is a list of the answers for the Q queries in order, separated by spaces.
Limits
Time limit: 40 seconds.
Memory limit: 1 GB.
1 ≤ T ≤ 100.
1 ≤ Q ≤ 5 × 104.
Si consists of uppercase English letters, for all i.
1 ≤ length of Si ≤ 20, for all i.
All Si are distinct.
1 ≤ Xi <Yi ≤ N, for all i.
Test Set 1
2 ≤ N ≤ 100.
Test Set 2
103 < N ≤ 5 × 104 in at most 10 cases.
2 ≤ N ≤ 103 in all other cases.
Sample
2 5 2 LIZZIE KEVIN BOHDAN LALIT RUOYU 1 2 1 3 2 2 KICK START 1 2 1 2
Case #1: 2 3 Case #2: -1 -1
In Sample Case #1, there are two queries:
- In the first query,
LIZZIEandKEVINare friends (because they share the letter E in their names). So, the shortest friendship chain length is 2. - In the second query,
LIZZIEandBOHDANare not friends, but have two possible shortest friendship chains (either viaKEVINorLALIT). So, the shortest friendship chain length is 3. Note that there are other friendship chains as well, but they are longer.
In Sample Case #2, there are two queries:
- In the first query,
KICKandSTARTare not connected by a chain of friends. - The second query is the same as the first query. Note that queries are not guaranteed to be distinct.
Analysis — A. Retype
Test set 1
We have already reached the level K. In order to calculate time taken to reach level K, start iterating from level 1 till level K and increment answer1 and answer2 on each step as we take 1 unit time to complete each level.
Test set 2
An observation here is that instead of simulating the levels and calculating the time taken, we can compute it in O(1) time. Initially, we are at level K. This means that we took K time units to reach level K as completing each level takes 1 unit of time. Hence, we can increment answer1 and answer2 by K directly.
Analysis — B. Boring Numbers
Test Set 1
Simply check all the numbers from L to R. Complexity = O((R-L) × log10(R)).
Test Set 2
We cannot follow the same approach as in Test Set 1 because the limits are too high. Let us calculate the number of boring numbers having exactly X digits first.
Lemma 1: There are 5 choices for digits at odd positions: {1,3,5,7,9}, and 5 choices for digits at even positions: {0,2,4,6,8}. Thus, the total number of boring numbers having exactly X digits is 5X.
Let us calculate the number of boring numbers less than or equal to R. The general idea is to split [1, R] into minimum number of intervals such that, all the numbers in an interval,
- Are of the same length.
- Have some(possibly none) prefix digits fixed.
- Positions following the fixed prefix can take any values from [0,9].
Let lengthinterval be the length of numbers in an interval. The intervals can thus be broken into two cases:
- 1. lengthinterval < length of R
- 2. lengthinterval = length of R
For example, let R = 3422. Number of boring numbers in [1, R] equals the number of boring numbers in [1,9] + [10, 99] + [100, 999] + [1000, 1999] + [2000, 2999] + [3000, 3099] + [3100, 3199] + [3200, 3299] + [3300, 3399] + [3400, 3409] + [3410, 3419] + [3420, 3422].
Case 1: This can be calculated using the fact that the total number of boring numbers having exactly X digits is 5X.
Case 2: Suppose R = d1,d2,d3,...,dlen. Intervals can be calculated by fixing some prefix of digits such that all numbers in the interval are less than R. For example, all numbers of the form, d1,..., di-1,ai,xi+1,xi+2,...,xlen, where ai < di and 0 ≤ xi+1,...,len ≤ 9.
If the fixed prefix does not obey the boring number's criteria, the number of boring number in the interval is 0. If it does, then, similar to Lemma 1, the number of boring numbers equals 5length of suffix.
Final answer = (number of boring numbers less than or equal to R) - (number of boring numbers less than or equal to L - 1).
Complexity = O(log10(R)).
Analysis — C. Rugby
We can divide this problem into two parts: choosing where to place the line, and choosing the permutation of players on the line (in other words, which players should be on which points on the line).
Regarding the permutation of players, the first observation that we can make is that preserving the initial X-ordering of the players is an optimal strategy. That means we should place the player with the lowest X coordinate value as the first player on the line, the player with the second lowest X coordinate value as the second player on the line, and so on. If there are ties, we can break them arbitrarily.
We can prove that this greedy strategy is optimal. First let us assume that there are two players with X-coordinates X1 and X2, and let us denote the X-coordinate of the start of line as startX, whereas X1 ≤ startX < X2. If we do not preserve the players' relative position on the final solution, we have that the first player will move for (startX + 1) - X1 steps, and the second player will move for X2 - startX steps, so the final solution equals -X1 + X2 + 1 steps. However, if we preserved the players' relative positions, the first player would move for startX - X1 steps, and the second player would move for X2 - (startX + 1) steps, so the final solution would equal -X1 + X2 - 1 steps, which is lower than the above strategy. For the other possible values of startX, which are startX < X1 or X2 ≤ startX, both permutations for the players result on the same amount of steps. Therefore, we can reach the conclusion that, for any solution, by swapping two players' order in order to preserve the players' initial relative positions, the total number of steps remains the same or decreases.
Now imagine that we have an arbitrary optimal solution S (not necessarily sorted on the players' X-coordinates). If we perform a swap, as described above, the solution does not get any worse, so it is still optimal. If we perform such a swap enough times we will reach a point in which the players are in non-descending order of their X coordinate, which is what our greedy solution looks like, and the solution is still optimal. Therefore, our greedy solution is optimal.
Regarding where to place the line, let solutionFirstX be the X position of the first point on the line, and let solutionRow be the Y position of the line.
Test Set 1
Given the constraints of the Test Set 1, we can iterate through all possible values for solutionFirstX and solutionRow and check which combination results on the minimum total number of steps. The grid is unbounded, however we can bound the possible values for solutionFirstX based on the initial X positions of the players, because placing the line entirely to the left of the player with the lowest X coordinate would make them all take an extra step to get there, which intuitively leads to a worse solution. The same applies on the right side. Let minPlayerX represent the X value of the player the most to the left, and maxPlayerX represent the X value of the player the most to the right. The number of possible values for solutionFirstX range between minPlayerX-(N-1) and maxPlayerX. Given similar definitions for minPlayerY and maxPlayerY, the same logic applies for solutionRow, which ranges between minPlayerY and maxPlayerY.
To calculate what is the total number of steps for the players to reach the line at candidateFirstX and candidateRow, iterate through all players in non-descending X-coordinate order and add their Manhattan distances to their relative locations on the line. In other words, the total number of steps equals the sum of |Xi - (candidateFirstX + (i - 1))| + |Yi - candidateRow|, for every player i in non-descending order of Xi.
The complexity of given solution is O(N × log N + (maxPlayerX - minPlayerX + N) × (maxPlayerY - minPlayerY + 1) × N).
Test Set 2
Given that the limits for N and the players initial positions are much greater in Test Set 2, the above mentioned solution would not be fast enough.
To divide our solution into smaller steps, we should notice that horizontal and vertical movement can be solved independently. In other words, the value solutionRow does not affect how many horizontal steps the players will take, as well as solutionFirstX does not affect how many vertical steps the players will take.
Let us start by finding the value for solutionRow. We can observe that most players will have to move vertically to reach solutionRow, either by moving up or moving down (and some will not have to move because they are initially on solutionRow). We want the total number of steps to be as small as possible, so a good candidate is the Y-position of the player that is positioned as the median among all players, regarding their initial Y-position.
We can prove that this is optimal as follows: first, let us start with the assumption that N is odd. If we set solutionRow to be equal to Y⌈N/2⌉ (the Y-position of the player in the middle), then we can see that there will be at least ⌊N/2⌋ players who are initially below or at the same line as the one in the middle, and at least ⌊N/2⌋ players who are initially above or at the same line as the one in the middle. Let us call totalStepsBelow the total number of steps taken by the ⌊N/2⌋ players who are initially below or at the same line as the one in the middle, and let us call totalStepsAbove the total number of steps taken by the ⌊N/2⌋ players who are initially above or at the same line as the one in the middle. As is, the total number of steps equals totalStepsBelow + totalStepsAbove. If we move solutionRow one position up, then the player in the middle and all the players that were initially below or at the same line as the one in the middle will have to take one extra step to reach solutionRow, and, in the best scenario, all the players that were initially above as the one in the middle will have to take one less step to reach solutionRow. Therefore, the total number of steps would equal (totalStepsBelow + ⌊N/2⌋ + 1) + (totalStepsAbove - ⌊N/2⌋), which equals totalStepsBelow + totalStepsAbove + 1, which is worse than our first guess. The same applies for moving solutionRow one position down. A similar logic can be used for when N is even.
Now we can use a similar approach for finding the value for solutionFirstX. Taking into account the fact that we want to preserve the players initial X-ordering, we can observe that for each player i, who has ki players to his left, the optimal value for solutionFirstX would be Xi - ki, because this way he would not have to move horizontally at all. Using the same logic described for finding solutionRow, we can find the optimal value for solutionFirstX by picking the median of all players optimal values for solutionFirstX.
Using these strategies we can find the value for solutionRow in O(N × log N) time by sorting the players by their initial Y-coordinate and picking the median value. Similarly, we can find the value for solutionFirstX in O(N × log N) time by sorting the players by their initial X-coordinate and picking the median optimal value. Finally we can calculate the total number of steps in O(N) time, by using the strategy mentioned on Test Set 1 analysis. Therefore, the time complexity of the solution is O(N × log N).
Analysis — D. Friends
Test Set 1
For this test set, we can build an undirected graph, where the nodes represent people and there is an edge between two nodes if and only if the names of the respective people have a common letter. Then each query can be answered by finding a shortest path between two nodes in the graph.
Assuming that L is the length of the longest name (recall that L ≤ 20), it is straightforward to build the graph in O(L2N2) time by considering each pair of nodes and using a nested pair of loops to look for a common letter in the names. The time complexity can be reduced to O(LN2) if we mark the letters of one of the names, and then iterate over the letters of the other name to see if any of those letters has been marked. A better yet approach is to represent the letters of a name as a 32-bit integer, where the i-th bit is 1 if the i-th letter of the alphabet is present in the name, and 0 otherwise. Then testing for common letters in two names boils down to checking if the logical AND of the respective bitmasks is non-zero, and thus the graph can be built in O(LN+N2) time.
The graph may have up to N × (N-1) / 2 edges, therefore, if we answer each query independently, say, using the breadth-first search, the overall time complexity of answering all Q queries is O(QN2), which might be too slow for large values of Q. Even if we never compute the answer for the same query twice by memoizing the results in a two-dimensional array, the time complexity is still O(N4).
A better alternative is to pre-compute the whole distance array in O(N3) time using the Floyd-Warshall algorithm or running breadth-first seach N times, once from each node. Then the individual queries can be answered in constant time and the overall time complexity becomes O(LN + N3 + Q).
Test Set 2
Here N can be large, so we really need an algorithm that is subquadratic in N. Let us look at the problem from a different angle. Using the first sample test case, consider the friendship graph below, and suppose that we need to find the length of the shortest friendship chain between LIZZIE and RUOYU.
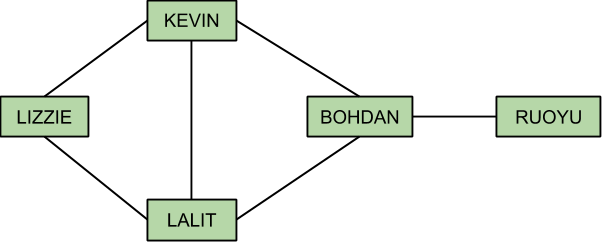
We start out with the set of letters L0 = {L,I,Z,E}. Since the names KEVIN and LALIT have at least one letter in L0, we know that the shortest friendship chain to these names has length 2. By extending our search to the names KEVIN and LALIT, we have reached the letters L1 = {K,V,N,A,T}. Since BOHDAN has some letters in L1 (N and A), the length of the shortest friendship chain from LIZZIE to BOHDAN is 3, and adding BOHDAN leads to a new set of letters L2 = {B,O,H,D}. The name RUOYU has the letter O in L2, therefore, the shortest friendship chain to RUOYU has length 4.
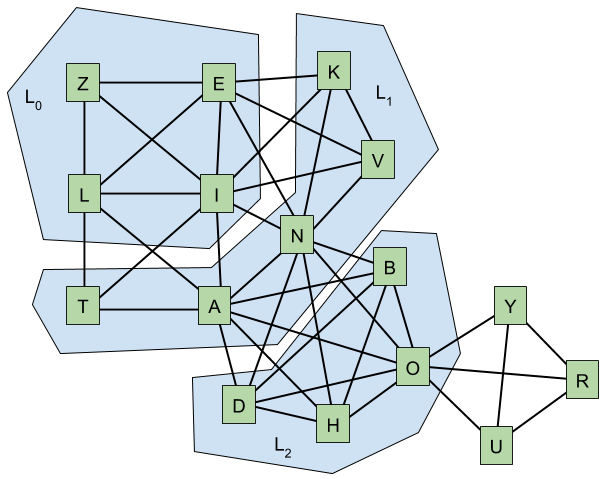
The crucial observation here is that we are essentially doing a breadth-first search in a very small graph G on the set of nodes {A,B,C,...,X,Y,Z}, where there is an edge between a pair of letters {u,v} if and only if the letters occur in the same name. The graph for our example is illustrated below.
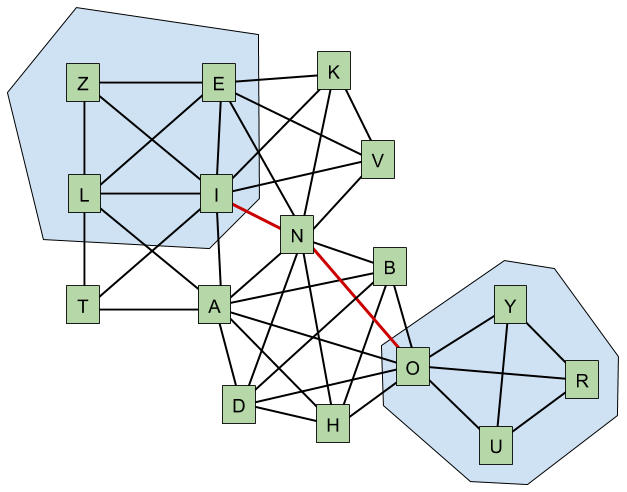
The goal of the breadth-first search was to find the shortest path connecting the sets of letters {L,I,Z,E} and {R,U,O,Y}. One of such paths is highlighted in red in the picture below. Instead of doing the breadth-first search, we could also pre-compute all-pairs shortest paths in G in constant time (yes, O(263) is still O(1)), and then answer each query in O(L2) time by taking the minimum distance over all pairs of letters {a,b}, where the letter a occurs in the first name, and the letter b occurs in the other name.
We can build the graph G in O(L2N) time by considering each of the input names and creating an edge between each pair of letters in the name. Consequently, the overall time complexity of the algorithm is O(L2(N+Q)).