Google Kick Start Archive — Round D 2020 problems

We can check whether the current element is the last element and, if not, if it is greater than the next element in constant time. To check whether i is a record breaking day, we also need to check whether the number of visitors of day i is greater than number of visitors from all the previous days.

Test Set 1

For each element j such that (1 <= j < i), check that the number of visitors on day j are less than number of visitors on day i. Hence, for each day we would compare it with all the previous days and it would take O(N) time. Therefore, for N days, the time complexity of this solution would be O(N^2).

Test Set 2

However that wouldn't be fast enough for Test Set 2, so we need a faster approach. Instead of comparing the number of visitors of day i against all the previous days one by one, we can compare the number of visitors of day i against the greatest number of visitors from all previous days. That reduces our processing time for each day from O(N) to O(1). Therefore, for N days, the time complexity of this solution would be O(N), which is sufficiently fast for both Test Set 1 and Test Set 2.

Sample Code (C++)

int countRecordBreakingDays(vector<int> visitors) {
  int recordBreaksCount = 0;
  int previousRecord = 0;
  for(int i = 0; i < checkpoints.size(); i++) {
     bool greaterThanPreviousDays = i == 0 || visitors[i] > previousRecord;
     bool greaterThanFollowingDay = i == checkpoints.size()-1 || visitors[i] > visitors[i+1];
     if(greaterThanPreviousDays && greaterThanFollowingDay) {
        recordBreaksCount++;
     }
     previousRecord = max(previousRecord, visitors[i]);
  }
  return recordBreaksCount;
}

Test Set 1

For the small test set, one can generate all possible conversions recursively and select the one with the smallest number of rule violations as the answer. Since each note can be converted to four possible notes in the alien scale, this results into 4^K combinations to be tested and O(4^K) time complexity.

Test Set 2

Dynamic Programming Solution

Let DP[i, j] be the minimum number of rule violations required to convert the first i notes A₁, A₂, ..., A_i such that the i-th note A_i is converted to note j of the alien piano (1 ≤ j ≤ 4). Then the answer is the minimum DP[K, j] over all j, 1 ≤ j ≤ 4.

The table DP[i, j] can be computed using dynamic programming as follows.
(1) DP[1, j] = 0 for all j.
(2) For i > 1, DP[i, j] = min{ DP[i - 1, j'] + P(i, j', j) | 1 ≤ j' ≤ 4 }. Here P(i, j', j) is a binary penalty term accounting for a rule violation between the notes A_i-1 and A_i. For example, if A_i-1 > A_i, then P(i, j', j) = 1 whenever j' ≤ j and P(i, j', j) = 0 otherwise.

Since each entry of the table is calculated using a constant number of operations, the overall time complexity of the algorithm is O(K), which is okay to pass the large test set.

Greedy Solution

Let us say that a sequence of pitches is playable if it can be converted to the alien piano notes without violating any rules. Our goal here is to split the given sequence of pitches into as few playable fragments as possible.

We can take the longest playable prefix of the sequence as the first fragment of the split. In this way, the remainder of the sequence is as short as possible, and therefore requires potentially fewer rule violations.

Now let us characterise the playable sequences. Note that repeated notes of the same pitch do not affect the playability of the sequence, therefore, without loss of generality, suppose that any two consecutive notes are at a different pitch. Let us say that two consecutive notes form an upward step if the second note has a higher pitch than the first. Otherwise, we call it a downward step.

Clearly, a sequence of notes is not playable if it contains more than three consecutive upward or downward steps, as we would run out of the alien scale. Otherwise, the sequence is playable and we can convert it using this simple strategy (assuming the note names A, B, C, and D of the alien piano from the lowest to the highest note):
(1) If the first step is upward, convert the first note to A.
(2) If the first step is downward, convert the first note to D.
(3) If three consecutive notes form an upward step followed by a downward step, convert the second note to D.
(4) If three consecutive notes form a downward step followed by an upward step, convert the second note to A.
(5) In all other cases, convert a note one step higher or lower than the note before depending on whether they form an upward or downward step.
Since any maximal sequence of upward steps starts at A and has no more than three steps (and similarly for any maximal sequence of downward steps), we will never leave the alien scale.

The following diagram illustrates the process of splitting the sequence (1, 8, 9, 7, 6, 5, 4, 3, 2, 1, 3, 2, 1, 3, 5, 7) into two playable fragments. Since the subsequence (9, 7, 6, 5, 4) consists of four downward steps, the sequence needs to be split between notes 5 and 4.

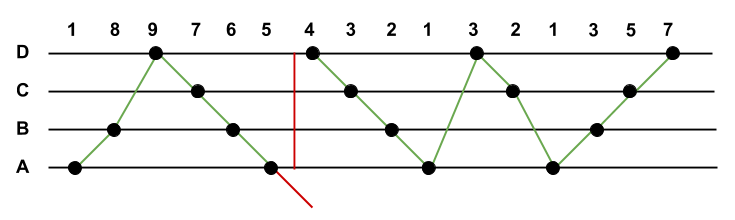
According to the analysis above, a single pass through the given sequence of notes maintaining the current number of consecutive upward and downward steps results in an O(K) solution, where K is the number of notes in the sequence. As soon as the number of upward or downward steps exceeds 3, we have to split the sequence by violating the rules and start a new fragment. A Python code snippet is included below for clarity.

def solve():
  k = input()
  a = map(int, raw_input().split())
  # Filter out repeated notes.
  a = [a[i] for i in xrange(0, k) if i == 0 or a[i - 1] != a[i]]
  upCount = 0
  downCount = 0
  violations = 0
  for i in xrange(1, len(a)):
    if a[i] > a[i - 1]:
      upCount += 1
      downCount = 0
    else:
      downCount += 1
      upCount = 0
    if upCount > 3 or downCount > 3:
      violations += 1
      upCount = downCount = 0
  return violations

For a given node, the P(visited by either Amadea or Bilva) = 1 - P(not visited by Amadea nor Bilva).
This leads to P(visited by either Amadea or Bilva) = 1 - ((1-P(visited by Amadea)) * (1-P(visited by Bilva)))
i.e. For a given node, note that events of visited-by-Amadea and visited-by-Bilva are mutually independent events, and hence P(being visited by either Amadea or Bilva) = P(visited by Amadea) + P(visited by Bilva) - (P(visited by Amadea)*P(visited by Bilva))

Given the above formula, our goal now is to find out P(visited by Amadea) and P(visited by Bilva) for every node in the tree. We can use DFS in order to do this.
Firstly, let's define 2 variables visits_a[] and visits_b[] where visits_a[i] and visits_b[i] denote the number of visits to node-i across all paths starting from any node in the subtree of node i with skips A and B respectively.

Now, the first DFS run would be from node-1 to compute visits_a[]. As we perform this DFS, we can keep a track of the path that has been taken so far, let's say path_taken[]. As we enter a node-i, we add it to path_taken[] and call DFS on it's children. Once we come back to node-i, we remove it from the path_taken[] and increment visit_a[i] by 1. Note that this increment is for the path leading from node-i to itself. Next, we check if there is some node-j which is A skips behind node-i. Using path_taken[], we check to see if such a node is present and increment the visits_a[node-j] by visits_a[i]. At the end of this DFS run, we have the total visit count for all nodes with the skip distance of A. Now, dividing visits_a[] by N gives us the P(visited by Amadea) for each node in the tree. Repeat the above process for to compute visits_b[] and obtain P(visited by Bilva) for every node in the tree.

With P(visited by Amadea) and P(visited by Bilva) computed for every node in the tree, computing and summing over P(being visited by either Amadea or Bilva) for each node will give us the answer. Since DFS takes linear time in the number of vertices, the time complexity of the solution is O(N).

Test Set 1

We can say that the rooms which Bangles has covered in the journey will always form a contiguous subarray. This is because, to go from room i to room j, Bangles must have unlocked the doors that occur between room i and room j once, only then Bangles would be able to move to room j. At any point of time, if Bangles has visited rooms from l to r, Bangles need to make a decision whether to go from room r to r+1 or from room l to l-1 depending which door has lower difficulty. Accordingly, Bangles can update l and r. For deciding which room to go next, it would take constant time. Thus, for taking K pictures, it would take O(K) time. K can be at most N. For each query, it would take O(N) time to process the query. Thus, overall complexity of the solution would be O(Q * N).

Test Set 2

The naive solution would time out for the constraints of test set 2. Thus, we can use the following approach to solve this:

Let InterestingLeft[i] be the door which is the closest door to the left of door i and has difficulty higher than door i. In case there is no such door, assign -1 to it. Similarly, let InterestingRight[i] be the door which is the closest door to the right of door i and has difficulty higher than door i. In case there is no such door, assign -1 to it. InterestingLeft[i] and InterestingRight[i] can be calculated by using the stack method in O(N) time.

After we are done unlocking the door i and all doors with difficulty lower than D[i] between doors InterestingLeft[i] and InterestingRight[i], we would either unlock door InterestingLeft[i] or door InterestingRight[i] next depending on which one has lower difficulty. If we have have only one choice, then we unlock that door itself. For generality, let us assume the next door that would be unlocked would be j. j would be equal to either InterestingLeft[i] or InterestingRight[i].

Let us construct a tree using the given relations. For each door i, we find such j and assign j as parent of i. We can see that a node can have at most 2 children: at most one from the left side and at most one from the right side. Thus the relations would form a Cartesian tree. From the given tree, we can make the following observations:

• If a node has only one child:
  • If the starting node is inside the subtree of current node, then the node will be visited only after all the nodes in its subtree have been visited.
  • If the starting node is outside the subtree of current node, then first the node will be visited and after that the nodes in its subtree will be visited.
• If a node has two children:
  • If the starting node is in left subtree, then first all the nodes in subtree of left child will be visited, then the current node will be visited, and finally the subtree of right child will be visited.
  • Similarly, if the starting node is in right subtree, then first all the nodes in subtree of right child will be visited, then the current node will be visited, and finally the subtree of left child will be visited.

Building this tree can be done in O(N) time because assigning the parents for each node according to InterestingLeft[i] and InterestingRight[i] takes constant time.

Let the subtree size of node i be Size[i]. Consider a query with starting room S and we need to find K-th room we will be in. Let the starting door X be the first door that we unlock. This can be determined in constant time by comparing the doors adjacent to room S. In the constructed tree, if size[X] < K, the whole subtree will be visited and we will move to its parent node. This will continue until we reach the node u such that size[u] ≥ K, so that we know that our answer lies within this subtree. To find such node, we can use the binary lifting approach similar to finding the lowest common ancestor between two nodes in a tree. This can be precomputed in O(N * log(N)) time. In a query we have following cases:

• If size[X] ≥ K, then:
  • If X is the door left to S, then answer is S - K.
  • Otherwise, answer is S+K.
• Otherwise, find node Y which is the first node on path from X to root such that size[Y] ≥ K. This can be done using binary lifting in O(logN). Now we can find the answer in constant time as follows:
  • If X < Y, then answer is Y + K - size[leftChild[Y]]
  • Otherwise, answer is Y + 1 - (K - size[rightChild[Y]])

Each query takes O(logN) time and building the binary tree and preprocessing for binary lifting takes O(N logN) time. Hence, overall complexity of the solution is O(N logN + Q logN).