Google Kick Start Archive — Round C 2020 problems

Test Set 1

For each element A_i, we can check whether it is a start of a K-countdown. In other words, we check whether A_{i + j} = K - j for all 0 ≤ j ≤ K. If the element A_i satisfies the condition, we can can increment our answer counter by 1. This solution runs in O(N × K).

Test Set 2

To solve this test set, we can loop through the elements and keep track of the number of consecutive elements such that the next element is one less than the previous element. We can do this by keeping a counter. If the current element is one less than the previous element, we increment this counter by 1. Otherwise, we reset the counter to 0. If the current element is 1 and our counter is at least K - 1, we know that the current element is the end of a K-countdown. We can increment our answer counter by 1 in this case.

This approach works since any pair of K-countdown subarrays does not overlap. This solution runs in O(N).

Pseudocode

  answer_counter = 0
  decreasing_counter = 0
  for (i = 1 to N - 1) {
    if (A[i] == A[i - 1] - 1) {
      decreasing_counter = decreasing_counter + 1
    } else {
      decreasing_counter = 0
    }
    if (A[i] == 1 and decreasing_counter >= K - 1) {
      answer_counter = answer_counter + 1
    }
  }
  print answer_counter

Test set 1

Each of the polyominos contains only one letter. We can take each of the permutations of the distinct letters, and check if the resulting wall is stable by following the order of the letters in the permutation to place the polyominos, one by one. There are N distinct letters in the input, so we will have N! permutations.

Let's say W is the given input wall letters. There are various ways to check if a wall is stable for a given permutation. One way is to create a new 2D array of integers, I. I[i][j] will contain the index of the letter W[i][j] in the permutation. Each of the letters at(i, j) in the wall must be placed after the letter below them, i.e. at(i+1, j), if they are not part of the same polyomino. We can check if it's true by checking if I[i][j] ≥ I[i+1][j], for all positions (i, j). Since I contains relative indexing of the order of the polyominos that were placed, this check works as intended. We can check this in O(R × C) time, so the runtime complexity of this approach for each test case is O(N! × R × C). This is sufficient for test set 1.

Test set 2

Given the picture of the wall, if two polyominos are positioned one above another, and they touch each other, then to make a stable wall, the bottom one must be placed before the top one. This gives us a set of orderings of pairs of letters which must be followed while placing the polyominos.

We can make a graph with the set of orderings just mentioned. Each polyomino/letter can be considered as a vertex, and each of the orderings can be considered as a directed edge of the graph. If the resulting graph contains any cycle, it is not possible to have a stable wall. Otherwise, we can use topological sort to find a suitable order that fulfills all the orderings. We can find all the orderings in O(R × C) time. We can find a topological sorting of the vertices of a directed acyclic graph by using depth first search. Depth first search gives us a runtime complexity of O(number of edges + number of vertices). The number of edges in the graph is at most (R-1) × C, as each cell of the grid adds at most one edge, to the cell right above it. So the total runtime complexity of this approach for each test case is O(R × C) + O(N + R × C) = O(R × C), since N can be at most R × C. This is sufficient for test set 2.

For test set 1, we can use the brute force approach to generate all subarray sums, check if each one is a square and return the total count. This would be enough to pass all the test cases under the time complexity.

For test set 2, looking at the problem constraints, we can estabilish that the largest subarray sum possible across all testcases would be N*MAX_A where MAX_A is the largest element in A. Therefore, we can precompute all squares ≤ N*MAX_A. This amounts to √(N*MAX_A) squares. Let's call this S[].

First, let's define Res[] where Res_i stores the number of subarrays ending at index i with subarray sum that is a perfect square.
Note: sum(A[L....R]) = sum(A[0.....R]) - sum(A[0....L-1]) for 0 < L ≤ R ≤ N..
Next, define an array P[] that keeps count of the number of indices i such that A[0...i] amount to a specific prefix_sum. i.e., P[prefix_sum] should give us the number of indices i such that sum(A[0...i])=prefix_sum. However, we could have negative prefix_sum values and hence P[prefix_sum] could be an invalid lookup. To resolve this, instead of mapping a prefix_sum to P[prefix_sum], we map it to P[prefix_sum + offset], where offset = min(sum(A[0.....i]), 0)*-1 for 0 ≤ i < N. i.e., The minimum among the N+1 (+1 for the empty prefix) prefix_sum values possible which can be computed with a single pass over A. Note that the offset is at least 0.

Next, we iterate the A left to right, while maintaining the sum of elements seen so far - let's call that prefix_sum. Now, at every i-th index, we ask the question, How many subarrays end at i and have the subarray sum which is also a square?
To answer this, we iterate S[] and for each square S_k, we add P[(prefix_sum-S_k) + offset] to Res[i]. Why so? - P is built as we iterate A and hence, at a certain index i, P holds the mapping of {prefix_sum, count} where count is the number of indices j (< i) such that sum(A[0....j])=prefix_sum. Therefore, P[(prefix_sum-S_k) + offset] holds the number of indices such that sum(A[j...i])=S_k.
We also increment the count of P[prefix_sum+offset] by 1 to record that sum(A[0....i])=prefix_sum. Finally, summing up all values Res[] would give us our answer.

Since we traverse A once, iterate S[] for every index i and lookup in P[] is O(1), the total time complexity for this solution is O(N*√(N*MAX_A)).

Appendix

A subtle observation and a potential improvement is to early exit on iteration of S[] at every stage. As mentioned earlier, we check P[(prefix_sum-S_k) + offset] and notice that at some point (prefix_sum-S_k) + offset could become < 0 which indicates not only that accessing P would be invalid, but also that S_k is too large to be obtained from all elements upto the current index i. We can use this criteria as a way to early exit the iteration on S[]. The asymptotic time complexity would remain the same, but would be slightly faster in run-time.

Next, instead of using an array with an offset for lookup of prefix sums , we could use a normal map, which would remove the need of an offset, but adds the cost of lookup that would take logarithmic time instead of the O(1). This solution may also be accepted if written efficiently and the time comoplexity would be O(N*log(N)*√(N*MAX_A)).

Let us ignore the update operations for now and look at how we can answer the queries efficiently. Take the array A = [5, 2, 7, 4, 6, 3, 9, 1, 8] as an example. The sweetness score for the query (1, 9) from l = 1 to r = 9 is intuitively visualized in the following diagram.

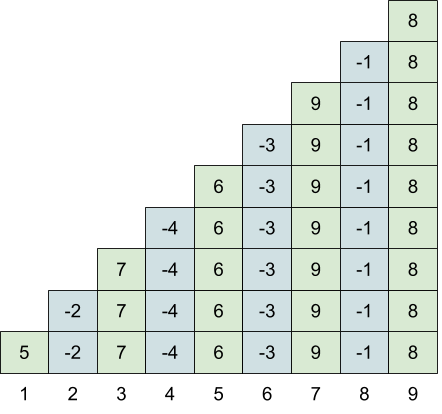
The i-th element (-1)^i-1A_i × i of the sweetness score sum is represented as a stack of i blocks in the i-th column of the diagram. The values in every other column are negated to account for the sign in the sweetness score sum. Obviously, the sum of all squares in the diagram is the sweetness score of the query (1, 9).

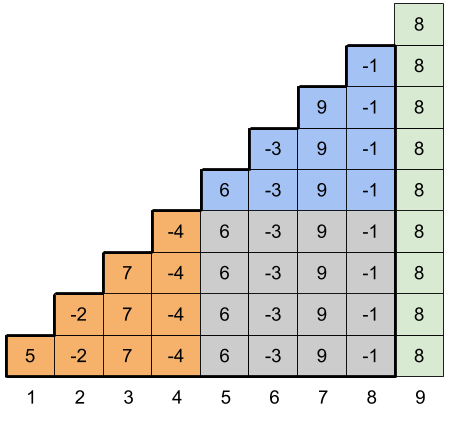
A crucial observation is that the sweetness scores for all other queries are embedded in the diagram as well. For example, the query (5, 8) corresponds to the blue shaded blocks in the diagram below, and the sweetness score of (5, 8) can be conveniently computed as the sum of all blocks inside the area with the bold outline minus the sum of orange and gray blocks. Note, however, that for queries (l, r) with even left endpoint l, we should take the additive inverse of the value computed this way to obtain the correct sweetness score.

Test Set 1

The above observations suggest a solution using prefix sums. Let us define the regular prefix sums S(i) as S(0) = 0 and S(i) = (-1)^i-1A_i + S(i - 1) for i ≥ 1. Similarly, let us define the multiple prefix sums MS(i) as MS(0) = 0 and MS(i) = (-1)^i-1A_i × i + MS(i - 1) for i ≥ 1. Then the sweetness score of a query (l, r) is
(-1)^l-1(MS(r) - MS(l - 1) - (l - 1) × (S(r) - S(l - 1))).

Computing the prefix sums takes O(N) time, and once we have them, each query can be answered in constant time. Therefore, the overall time complexity of the algorithm is O(N + Q).

So far we have disregarded the update operations, however, since there are no more than 5 of them, we can recompute the prefix sums after each update operation without increasing the time complexity.

Test Set 2

Here the number of update operations is unlimited, and the time complexity of the previous algorithm becomes O(NQ), which is inefficient. However, we can still use very much the same idea by maintaining two segment trees – a tree T for storing the values (-1)^i-1A_i and another tree MT for storing the values (-1)^i-1A_i × i. Then the answer to a query (l, r) becomes (-1)^l-1(MT.rangeSum(l, r) - (l - 1) × T.rangeSum(l, r)).

Since updates and range queries in a segment tree take O(log N) time, the overall time complexity of the algorithm is O(N + Q log N).