Google Kick Start Archive — Round D 2017 problems
Overview
This Kickstart Round consists of a classic Dynamic Programming problem, a Binary Search problem with a lot to code and a "geometry" problem.
Thanks to everyone who participated! Kickstart Round E will take place next month; check the Kickstart schedule for more details.
Cast
Problem A (Go Sightseeing): Written and prepared by Celestine Lau.
Problem B (Sherlock and The Matrix Game): Written and prepared by Lalit Kundu.
Problem C (Trash Throwing): Written and prepared by Chao Li.
Solutions and other problem preparation and review by Ian Tullis, Yiming Li, Xuanang Zhao, Yan Li, Trung Thanh Nguyen and Sunny Aggarwal. Thanks for their help!
Analysis authors:
- Go Sightseeing: Celestine Lau
- Sherlock and The Matrix Game: Lalit Kundu
- Trash Throwing: Chao Li
A. Sightseeing
Problem
When you travel, you like to spend time sightseeing in as many cities as possible, but sometimes you might not be able to because you need to catch the bus to the next city. To maximize your travel enjoyment, you decide to write a program to optimize your schedule.
You begin at city 1 at time 0 and plan to travel to cities 2 to N in ascending order, visiting every city. There is a bus service from every city i to the next city i + 1. The i-th bus service runs on a schedule that is specified by 3 integers: Si, Fi and Di, the start time, frequency and ride duration. Formally, this means that there is a bus leaving from city i at all times Si + xFi, where x is an integer and x ≥ 0, and the bus takes Di time to reach city i + 1.
At each city between 1 and N - 1, inclusive, you can decide to spend Ts time sightseeing before waiting for the next bus, or you can immediately wait for the next bus. You cannot go sightseeing multiple times in the same city. You may assume that boarding and leaving buses takes no time. You must arrive at city N by time Tf at the latest. (Note that you cannot go sightseeing in city N, even if you arrive early. There's nothing to see there!)
What is the maximum number of cities you can go sightseeing in?
Input
The input starts with one line containing one integer T, which is the number of test cases. T test cases follow.
Each test case begins with a line containing 3 integers, N, Ts and Tf, representing the number of cities, the time taken for sightseeing in any city, and the latest time you can arrive in city N.
This is followed by N - 1 lines. On the i-th line, there are 3 integers, Si, Fi and Di, indicating the start time, frequency, and duration of buses travelling from city i to city i + 1.
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1) and y is
the maximum number of cities you can go sightseeing in such that you can still
arrive at city N by time Tf at the latest. If it is
impossible to arrive at city N by time Tf, output
Case #x: IMPOSSIBLE.
Limits
1 ≤ T ≤ 100.Time limit: 20 seconds per test set.
Memory limit: 1GB.
Small dataset (Test set 1 - Visible)
2 ≤ N ≤ 16.1 ≤ Si ≤ 5000.
1 ≤ Fi ≤ 5000.
1 ≤ Di ≤ 5000.
1 ≤ Ts ≤ 5000.
1 ≤ Tf ≤ 5000.
Large dataset (Test set 2 - Hidden)
2 ≤ N ≤ 2000.1 ≤ Si ≤ 109.
1 ≤ Fi ≤ 109.
1 ≤ Di ≤ 109.
1 ≤ Ts ≤ 109.
1 ≤ Tf ≤ 109.
Sample
4 4 3 12 3 2 1 6 2 2 1 3 2 3 2 30 1 2 27 3 2 1 4 1 11 2 1 2 4 1 5 8 2 2 5 10 5000 14 27 31 27 11 44 30 8 20 2000 4000 3
Case #1: 2 Case #2: 0 Case #3: IMPOSSIBLE Case #4: 4
In the first test case, you can go sightseeing in city 1, catching the bus leaving at time 3 and arriving at time 4. You can go sightseeing in city 2, leaving on the bus at time 8. When you arrive in city 3 at time 10 you immediately board the next bus and arrive in city 4 just in time at time 12.
B. Sherlock and Matrix Game
Problem
Today, Sherlock and Watson attended a lecture in which they were introduced to matrices. Sherlock is one of those programmers who is not really interested in linear algebra, but he did come up with a problem involving matrices for Watson to solve.
Sherlock has given Watson two one-dimensional arrays A and B; both have length N. He has asked Watson to form a matrix with N rows and N columns, in which the jth element in the ith row is the product of the i-th element of A and the j-th element of B.
Let (x, y) denote the cell of the matrix in the x-th row (numbered starting from 0, starting from the top row) and the y-th column (numbered starting from 0, starting from the left column). Then a submatrix is defined by bottom-left and top-right cells (a, b) and (c, d) respectively, with a ≥ c and d ≥ b, and the submatrix consists of all cells (i, j) such that c ≤ i ≤ a and b ≤ j ≤ d. The sum of a submatrix is defined as sum of all of the cells of the submatrix.
To challenge Watson, Sherlock has given him an integer K and asked him to output the Kth largest sum among all submatrices in Watson's matrix, with K counting starting from 1 for the largest sum. (It is possible that different values of K may correspond to the same sum; that is, there may be multiple submatrices with the same sum.) Can you help Watson?
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case consists of one line with nine integers N, K, A1, B1, C, D, E1, E2 and F. N is the length of arrays A and B; K is the rank of the submatrix sum Watson has to output, A1 and B1 are the first elements of arrays A and B, respectively; and the other five values are parameters that you should use to generate the elements of the arrays, as follows:
First define x1 = A1, y1 = B1, r1 = 0, s1 = 0. Then, use the recurrences below to generate xi and yi for i = 2 to N:
- xi = ( C*xi-1 + D*yi-1 + E1 ) modulo F.
- yi = ( D*xi-1 + C*yi-1 + E2 ) modulo F.
- ri = ( C*ri-1 + D*si-1 + E1 ) modulo 2.
- si = ( D*ri-1 + C*si-1 + E2 ) modulo 2.
Output
For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is the Kth largest submatrix sum in the matrix defined in the statement.
Limits
1 ≤ T ≤ 20.
Memory limit: 1GB.
1 ≤ K ≤ min(105, total number of submatrices possible).
0 ≤ A1 ≤ 103.
0 ≤ B1 ≤ 103.
0 ≤ C ≤ 103.
0 ≤ D ≤ 103.
0 ≤ E1 ≤ 103.
0 ≤ E2 ≤ 103.
1 ≤ F ≤ 103.
Small dataset (Test set 1 - Visible)
Time limit: 40 seconds.
1 ≤ N ≤ 200.
Large dataset (Test set 2 - Hidden)
Time limit: 200 seconds.
1 ≤ N ≤ 105.
Sample
3 2 3 1 1 1 1 1 1 5 1 1 2 2 2 2 2 2 5 2 3 1 2 2 1 1 1 5
Case #1: 6 Case #2: 4 Case #3: 1
[1, -3]
[-3, 9]
All possible submatrix sums in decreasing order are [9, 6, 6, 4, 1, -2, -2, -3, -3]. As K = 3, answer is 6.
In case 2, using the generation method, the generated arrays A and B are [2] and [2], respectively. So, the matrix formed is
[4]
As K = 1, answer is 4.
In case 3, using the generation method, the generated arrays A and B are [1, 0] and [2, -1] respectively. So, the matrix formed is
[2, -1]
[0, 0]
All possible submatrix sums in decreasing order are [2, 2, 1, 1, 0, 0, 0, -1, -1]. As K = 3, answer is 1.
C. Trash
Problem
Bob is an outstanding Googler. He loves efficiency, so he does everything well and quickly. Today, Bob has discovered that the trash can near his desk has disappeared! Sadly, this means that he has to use another nearby trash can instead. Since getting out of his seat to use the trash can would lower his productivity, Bob has decided to throw his trash into that trash can!
But there are many obstacles in the Google office. For example, it is rude if the thrown trash hits somebody, or the wall, or anything else. Bob hopes to throw the trash without touching any existing obstacles.
To simplify this problem, we will only consider the vertical plane that includes Bob and the trash can. Bob is at point (0, 0); the trash can is at point (P, 0). Moreover, there are N obstacles in the office; each of them is a single point, and the i-th one has coordinates (Xi, Yi). The ceiling of the office is a line with the expression y=H in the plane. Since Bob is in one of the new high-tech floating offices, we do not consider the office floor in this problem; you do not need to worry about collisions with it. Bob will throw a piece of trash that is a circle with radius R. The center of the piece of trash starts off at (0, 0). When the piece of trash is thrown, the center of the piece of trash must follow the path of a parabola with the expression f(x)=ax(x-P), where 0 ≤ x ≤ P, and a can be any real number less than or equal to 0. The piece of trash is only considered thrown away when its center reaches the trash can's point, and it is not enough for some part of the piece of trash to just touch that point.
Bob is wondering: what is the largest piece of trash he can throw without hitting the ceiling or any obstacles? That is, we must find the maximum value of R for which there is at least one value a that satisfies the following: for any 0 ≤ x ≤ P, the Euclidean distance between (x, f(x)) and (x, H) is greater than R, and for each i, the Euclidean distance between the point (x, f(x)) and (Xi, Yi) is greater than or equal to R.
Input
The input starts with one line containing one integer T, the number of test cases. T test cases follow. The first line of each test case contains three integers N, P, and H: the number of obstacles, the x-coordinate of the trash can, and the height of the ceiling. Then, there are N more lines; the i-th of those lines represents the i-th obstacle, and has two integers Xi and Yi, representing that obstacle's coordinates.
Output
For each test case, output one line Case #x: y, where
x is the test case number (starting from 1) and y is
a double representing the maximum radius R. Your answer will be
considered correct if it is within an absolute or relative error of
10-4 of the correct answer. See the
FAQ for an explanation
of what that means, and what formats of real numbers we accept.
Limits
1 ≤ T ≤ 50.Time limit: 120 seconds per test set.
Memory limit: 1GB.
2 ≤ P ≤ 1000.
2 ≤ H ≤ 1000.
0 < Xi < P.
0 < Yi < H.
Small dataset (Test set 1 - Visible)
N = 1.Large dataset (Test set 2 - Hidden)
1 ≤ N ≤ 10.Sample
4 1 10 10 5 3 1 10 10 5 4 1 100 10 50 3 2 10 10 4 2 6 7
Case #1: 3.23874149472 Case #2: 4.0 Case #3: 3.5 Case #4: 2.23145912401
Note that the last sample case would not appear in the Small dataset.
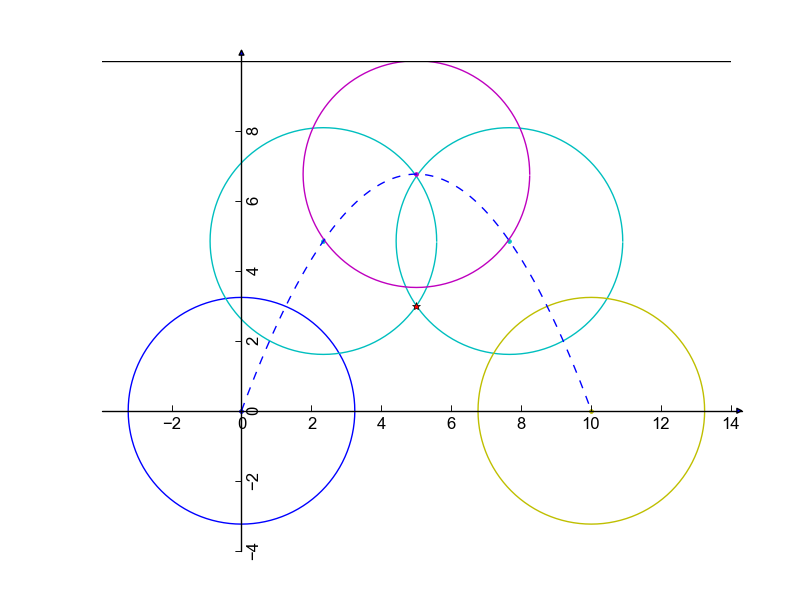
The following picture illustrates Sample Case #1. Bob is at (0, 0), and the trash can is at (10, 0). There is a obstacle at point (5, 3), marked with a star. If Bob throws trash over the top of the obstacle, the maximal R is 3.2387, which requires an a of about -0.2705. If Bob throws trash under the obstacle, the maximal R is 3, which requires an a of 0. So the maximum R for this case is about 3.2387.
Sample Case #2 is like Sample Case #1, but the obstacle is one unit higher. Now, if Bob throws the trash under the obstacle, the maximal R is 4 (for a = 0). If he throws the trash over the obstacle, he can only use trash with a radius up to about 2.8306 (with a = -0.4). So the maximum R for this case is 4.
Analysis — A. Sightseeing
Go Sightseeing: Analysis
Small dataset
There are at most 15 cities in which you can go sightseeing, and in each of those cities, we can either go sightseeing or not, so there are only 215 possibilities to consider. A brute force approach that tries each of those 215 possibilities is fast enough. For each possibility, we can compute the earliest possible time of arrival in city N and then find the possibility with the greatest number of sightseeing trips that arrives at city N on time.
It can be observed that the time of arrival in any city i + 1 is only dependent on Tw, the time at which we start waiting for the bus in city i. This can be expressed as Arrival(i + 1, Tw) = T' + Di - ((T' - Si) mod Fi), where T' is max(Tw, Si). The arrival time at the final city can thus be computed by iteratively applying the Arrival() function to each city in succession. Tw for city i will equal Arrival(i) if we do not go sightseeing in city i, and Arrival(i) + Ts if we do.
Large dataset
A brute force approach will not work for the large dataset as there are now 2000 cities. However, as noted above, the time of arrival in any city is only dependent on the time that we start waiting at the previous city. This allows us to use dynamic programming to solve this problem.
One option that might come to mind is to compute m(i, j), the maximum number of cities that you can go sightseeing in if you have reached city i by time j. This can easily be expressed as a recurrence relation on smaller values of i and j. However, since the times can be as large as 109, this approach is not possible. Instead, we should try to compute f(i, j), the earliest time we can arrive at city i, after having gone sightseeing at exactly j different cities. For the base case of f(2, 0), this is equal to Arrival(2, 0) as defined above, while f(2, 1) = Arrival(2, Ts).
To obtain the recurrence relation, consider a particular city i, where i > 1. You can either choose to go sightseeing there, or not. If you do, then that delays your departure time by Ts but adds 1 to the total number of cities in which you have gone sightseeing. This relationship can be captured as the following equation:
f(i, j) = min(Arrival(i, f(i - 1, j)), Arrival(i, f(i - 1, j - 1) + Ts))
Once we have computed all possible f, the answer can be obtained by finding the maximum value of x such that f(N, x) ≤ Tf. This solution runs in O(N2) time.
Analysis — B. Sherlock and Matrix Game
Sherlock and The Matrix Game : Analysis
Brute force approaches
In the Small dataset, N (which is the size of arrays A and B) doesn't exceed 200. A naive bruteforce strategy is to actually create the matrix and then iterate over all possible submatrices and calculate the sum for each submatrix. Since the number of submatrices is O(N4) (observe that for every pair of cells, there exists a unique submatrix), naively iterating over each submatrix in O(submatrix size) is bound to run for years(it's a whopping 1.2 * 1015 operations for 20 test cases in the worst case). However, if we can calculate sum of each submatrix in constant time, the number of operations will reduce to 3 * 1010, which is feasible for a modern machine in minutes.
Inclusion-exclusion to the rescue
Quickly calculating submatrix sums of a matrix M can be done by maintaining another matrix P such that P(i, j) = sum of all cells M(a, b), such that 1 ≤ a ≤ i and 1 ≤ b ≤ j. Matrix P can be built in O(size of M) time by using the recurrence P(i, j) = M(i, j) + P(i-1, j) + P(i, j-1) - P(i-1, j-1). Note that the first three terms on the right hand side count some of the cells twice, which is why we subtract off the fourth term. Further, the sum of a submatrix defined by top-left and bottom-right cells (a, b) and (c, d) can be calculated as P(c, d) - P(a-1, d) - P(c, b-1) + P(a-1, b-1). Again, we add the last term on right hand side to accomodate the double subtraction of some cells.
A binary search large approach
For the Large dataset, N could be up to 105, which implies that creating the matrix in-memory is not possible, let alone iterating over all possible submatrices. We can, however, use the fact that M(i, j) = Ai * Bj to our advantage by expressing sum of cells in the submatrix defined by top-left and bottom-right cells (a, b) and (c, d), respectively, as (Aa + Aa+1 + ... + Ac) * (Bb + Bb+1 + ... + Bd), i.e., product of sum of contiguous subarrays of A and B.
If we create two sorted lists U and V consisting of all possible subarray sums of A and B, respectively, we're trying to find the Kth largest value among Ui * Vj for all i, j. At this moment, we can exploit the fact that K doesn't exceed 105 by observing that we don't need to consider all possible values in U and V. We can work with the K largest and smallest values from both arrays(why the smallest? don't forget we also have negative values?) and be guaranteed that answer will be present in product of these values. At this point, we face two subproblems to finally solve this problem.
Subproblem 1
Given an array A of size N, find the K largest subarray sums of A. Note that the value of K is approximately O(N). If we can do this, finding the K smallest subarray sums is easy by reversing the signs of values in A and running the same algorithm.
Solution
We use binary search! The idea is to first find the Kth largest subarray sum
by binary searching for it, and then build the actual subarray sums. To apply binary search for
the Kth largest subarray sum, we need a function which can quickly count:
how many subarray sums are less than X, for a given X?
Let us define Pi as sum of the first i
elements of array A. Now, a simple idea is to iterate over i and
fix the subarray start at position i. Now, we're trying to count
possible j(≥ i) such that
Pj ≥ Pi + X.
Note that the right size of the inequality is a constant for a fixed i.
Things would've been easier if prefix sum array P had been an increasing sequence.
However, that is not the case, since there are also negative values in array A.
Suppose that we iterate over i from N to 1. At each step, we'll try to calculate
the answer for i(which depends on all values Aj such
that j ≥ i). Imagine we have a data structure DS
which supports two operations:
- Insert y : inserts y in the data structure.
- Query y : returns the count of values present in data structure that are less than or equal to y.
Subproblem 2
Given two arrays A and B of size O(N), find the Kth largest among all possible values Ai * Bj, for all i, j.
Solution
Again, we can use binary search on our answer if we, given X, can count how many pairs
i, j exist such that Ai *
Bj ≥ X.
Just as in to subproblem 1, the idea is to iterate over i, and then count all
possible j such that
Bj ≥ X / Ai,
which is easily doable using binary search if array B is kept in a sorted fashion.
However, note that it is a little trickier because of negative values. The complexity of solving this
subproblem turns out to be (log(range of answer) * N * log(N)).
Analysis — C. Trash
Trash Throwing: Analysis
In this problem, we will use binary search multiple times to transform an optimization problem into a decision problem. The problem asks us to find the maximal radius for a thrown circle with a center position satisfying f(x)=ax(x-P), without touching the ceiling or any obstacles.
First of all, if there is an a so that a circle with radius R could pass, then for all R' ≤ R, R' is also a valid solution, as we can choose the same a. In other words, we can binary search on R, and for each R, check whether there is a valid a. If there is, R is an acceptable answer.
How can we determine whether there is a valid parabola for a given R?
Let's convert the problem into a simpler form. Bob wants to throw a circle without touching any obstacles. That is, for any point on the parabola (x, f(x)), the distance from that point to the obstacle (Xi, Yi) must be larger than R. We can reframe the problem as follows: given some obstacle circles, with the i-th circle centered at (Xi, Yi) with radius R, Bob will throw a point such that the point does not touch/enter any circles. (We must also lower the ceiling by exactly R units.) This conversion does not change the final answer.
In the Small dataset, there is only one obstacle, as shown in example, and there are two ways to throw it into the trash can. One way is to throw the point over the obstacle, and the other one is to throw the point under the obstacle. Let's consider the former situation. If there is an a for which the parabola does not touch the obstacle circle, then for all a' ≤ a, the parabola with parameter a' is a valid solution. Therefore, we can binary search again (this time on a) and get an interval of real numbers that are valid value of a. The latter situation is similar. After we have considered both situations, we will have two (or maybe one, in a corner case) intervals of possible values for a.
After we binary search to find R and a, the problem becomes,
given the parabola parameter a and an obstacle circle with radius
R, determine whether the parabola will intersect the circle.
We can list the equations:
y = ax(x-P)
(x - Xi)2 + (y - Yi)2 =
R2
Since a, P, Xi, Yi and
R are all known variables, we can solve the equations by
Newton's method
or
Ferrari's algorithm.
Each real root represents an intersection point of the parabola and the
circle, so an a is acceptable if the equations do not have real roots.
As for the ceiling case, since the parabola gets the maximal f(x) when
x=P/2, if the maximal f(x) is lower than
H-R, the trash will not touch the ceiling.
This is enough to solve the Small dataset.
Finally, let us handle the case of multiple obstacles. We can use the same binary search mechanism. Note that in the previous solution for one obstacle, after binary search for R, we used another binary search to find the valid intervals for a. What we need to do is to find a value of a that is valid for all the obstacles. We can do this by masking all invalid intervals, and seeing what remains. If the invalid intervals cover all real numbers, then the value of R that we are considering is not acceptable.