Google Code Jam Archive — Round 1A 2022 problems
Overview
Round 1A started with Double or One Thing that surely required double the normal thinking to solve. Next, Equal Sum was a unique interactive problem that had contestants solving an NP-complete problem with a twist. Finally, Weightlifting gave contestants a good workout while they optimized the ordering of weights on an exercise machine.
Benq was the first one with a perfect score, and that gave them the top position in the final standings. ecnerwala and Geothermal rounded out the top 3 with only a few more minutes of penalty. More than 300 people managed a perfect score. Over 9000 people scored some points out of the more than 10000 that submitted a solution.
When the hidden results were revealed, the contestant in 1500th place had 56 points, which is the unofficial cutoff for advancing. Come back once results are finalized to see the final look of the scoreboard.
Congratulations to all advancers! If you did not advance, you have two more chances in Round 1B and Round 1C. See the schedule to find out when and mark your calendar!
Cast
Double or One Thing: Written by Pablo Heiber. Prepared by Shantam Agarwal.
Equal Sum: Written by Pablo Heiber. Prepared by Artem Iglikov.
Weightlifting: Written by Thomas Tellier. Prepared by Yang Xiao.
Solutions and other problem preparation and review by Abhilash Tayade, Aditya Mishra, Antonio Mendez, Apoorv Agarwal, Chakradhar Reddy, Chu-ling Ko, Darcy Best, Deepak Gour, Ikumi Hide, Liang Bai, Md Mahbubul Hasan, Mohamed Yosri Ahmed, Nafis Sadique, Nhi Le, Nikita Rungta, Pablo Heiber, Pi-Hsun Shih, Priyam Khandelwal, Sudarsan Srinivasan, Swapnil Gupta, Swapnil Mahajan, Timothy Buzzelli, Ulises Mendez Martinez, Vaibhav Tulsyan, Yang Xiao, Yeabkal Wubshit, and Yui Hosaka.
Analysis authors:
- Double or One Thing: Chu-ling Ko.
- Equal Sum: Pablo Heiber.
- Weightlifting: Pablo Heiber.
A. Double or One Thing
Problem
You are given a string of uppercase English letters. You can highlight any number of the letters (possibly all or none of them). The highlighted letters do not need to be consecutive. Then, a new string is produced by processing the letters from left to right: non-highlighted letters are appended once to the new string, while highlighted letters are appended twice.
![]()
For example, if the initial string is HELLOWORLD, you could highlight the
H, the first and last Ls and the last O to obtain
HELLOWORLD
$$$\Rightarrow$$$
HHELLLOWOORLLD. Similarly, if you highlight nothing, you obtain
HELLOWORLD, and if you highlight all of the letters, you obtain
HHEELLLLOOWWOORRLLDD. Notice how each occurrence of the same letter can be highlighted
independently.
Given a string, there are multiple strings that can be obtained as a result of this process, depending on the highlighting choices. Among all of those strings, output the one that appears first in alphabetical (also known as lexicographical) order.
Note: A string $$$s$$$ appears before a different string $$$t$$$ in alphabetical order
if $$$s$$$ is a prefix of $$$t$$$ or if at the first place $$$s$$$ and $$$t$$$ differ,
the letter in $$$s$$$ is earlier in the alphabet than the letter in $$$t$$$. For example,
these strings are in alphabetical order:
CODE, HELLO, HI, HIM, HOME,
JAM.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow. Each test case is described in a single line containing a single string $$$\mathbf{S}$$$.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$,
where $$$x$$$ is the test case number (starting from 1) and $$$y$$$ is the string that
comes first alphabetically from the set of strings that can be produced from $$$\mathbf{S}$$$ by the
process described above.
Limits
Time limit: 2 seconds.
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
Each character of $$$\mathbf{S}$$$ is an uppercase letter from the English alphabet.
Test Set 1 (Visible Verdict)
$$$1 \le $$$ the length of $$$\mathbf{S} \le 10$$$.
Test Set 2 (Hidden Verdict)
$$$1 \le $$$ the length of $$$\mathbf{S} \le 100$$$.
Sample
3 PEEL AAAAAAAAAA CODEJAMDAY
Case #1: PEEEEL Case #2: AAAAAAAAAA Case #3: CCODDEEJAAMDAAY
In Sample Case #1, these are all the strings that can be obtained, in alphabetical order:
PEEEEL,
PEEEELL,
PEEEL,
PEEELL,
PEEL,
PEELL,
PPEEEEL,
PPEEEELL,
PPEEEL,
PPEEELL,
PPEEL, and
PPEELL.
In Sample Case #2, every string that can be obtained contains only As. The
shortest of those is alphabetically first, because it is a prefix of all others.
In Sample Case #3, there are $$$1024$$$ possible strings which can be generated from
CODEJAMDAY out of which CCODDEEJAAMDAAY is the lexicographically
smallest one.
B. Equal Sum
Problem
You are given a set of distinct integers. You need to separate them into two non-empty subsets such that each element belongs to exactly one of them and the sum of all elements of each subset is the same.
An anonymous tip told us that the problem above was unlikely to be solved in polynomial time (or something like that), so we decided to change it. Now you get to decide what half of the integers are!
This is an interactive problem with three phases. In phase 1, you choose $$$\mathbf{N}$$$ distinct integers. In phase 2, you are given another $$$\mathbf{N}$$$ integers that are distinct from each other and from the ones you chose in phase 1. In phase 3, you have to partition those $$$2\mathbf{N}$$$ integers into two subsets, both of which sum to the same amount. All $$$2\mathbf{N}$$$ integers are to be between $$$1$$$ and $$$10^9$$$, inclusive, and it is guaranteed that they sum up to an even number.
Input and output
This is an interactive problem. You should make sure you have read the information in the Interactive Problems section of our FAQ.
Initially, your program should read a single line containing an integer, $$$\mathbf{T}$$$, the number of test cases. Then, $$$\mathbf{T}$$$ test cases must be processed.
For each test case, your program must first read a line containing a single integer $$$\mathbf{N}$$$. Then, it must output a line containing $$$\mathbf{N}$$$ distinct integers $$$A_1, A_2, \dots, A_\mathbf{N}$$$. Each of these integers must be between $$$1$$$ and $$$10^9$$$, inclusive. After that, your program must read a line containing $$$\mathbf{N}$$$ additional integers $$$\mathbf{B_1}, \mathbf{B_2}, \dots, \mathbf{B_N}$$$. Finally, your program must output a line containing between $$$1$$$ and $$$2\mathbf{N}-1$$$ integers from among $$$A_1, A_2, \dots, A_\mathbf{N}, \mathbf{B_1}, \mathbf{B_2}, \dots, \mathbf{B_N}$$$: the ones chosen to be part of the first subset. The integers from $$$A$$$ and $$$\mathbf{B}$$$ that you do not output are considered to be part of the other subset.
The next test case starts immediately if there is one. If this was the last test case, the judge will expect no more output and will send no further input to your program. In addition, all $$$\mathbf{T}$$$ test cases are always processed, regardless of whether the final output from your program is correct or not.
Note: It can be shown that given the limits for this problem, there exists a sequence $$$A_1, A_2, \dots, A_\mathbf{N}$$$ such that any sequence $$$\mathbf{B_1}, \mathbf{B_2}, \dots, \mathbf{B_N}$$$ results in a set of $$$2\mathbf{N}$$$ integers that can be separated into two subsets with equal sums.
If the judge receives an invalidly formatted or invalid line (like outputting an unexpected number of integers, or integers out of range, or repeated integers in a line) from your program at any moment, the judge will print a single number $$$-1$$$ and will not print any further output. If your program continues to wait for the judge after receiving a $$$-1$$$, your program will time out, resulting in a Time Limit Exceeded error. Notice that it is your responsibility to have your program exit in time to receive a Wrong Answer judgment instead of a Time Limit Exceeded error. As usual, if the memory limit is exceeded, or your program gets a runtime error, you will receive the appropriate judgment.
Limits
Time limit: 5 seconds.
Memory limit: 1 GB.
Test Set 1 (Visible Verdict)
$$$1 \le \mathbf{T} \le 100$$$.
$$$\mathbf{N} = 100$$$.
$$$1 \le \mathbf{B_i} \le 10^9$$$, for all $$$i$$$.
$$$\mathbf{B_i} \neq A_j$$$, for all $$$i, j$$$.
$$$\mathbf{B_i} \neq \mathbf{B_j}$$$, for all $$$i \neq j$$$.
For each test case, the judge will choose the $$$\mathbf{B_i}$$$s such that the sum of all $$$2\mathbf{N}$$$ integers is even.
Testing Tool
You can use this testing tool to test locally or on our platform. To test locally, you will need to run the tool in parallel with your code; you can use our interactive runner for that. For more information, read the instructions in comments in that file, and also check out the Interactive Problems section of the FAQ.
Instructions for the testing tool are included in comments within the tool. We encourage you to add your own test cases. Please be advised that although the testing tool is intended to simulate the judging system, it is NOT the real judging system and might behave differently. If your code passes the testing tool but fails the real judge, please check the Coding section of the FAQ to make sure that you are using the same compiler as us.
2
3
5 1 3
10 4 9
1 10 5
This is correct because $$$1+5+10=16=3+4+9$$$.
3
5 2 3
10 8 12
12 8
This is correct because $$$8+12=20=2+3+5+10$$$.
C. Weightlifting
Problem
You are following a prescribed training for weightlifting. The training consists of a series of exercises that you must do in order. Each exercise requires a specific set of weights to be placed on a machine.
There are $$$\mathbf{W}$$$ types of different weights. For example, an exercise may require $$$3$$$ weights of type A and $$$1$$$ weight of type B, while the next requires $$$2$$$ weights each of types A, C, and D.
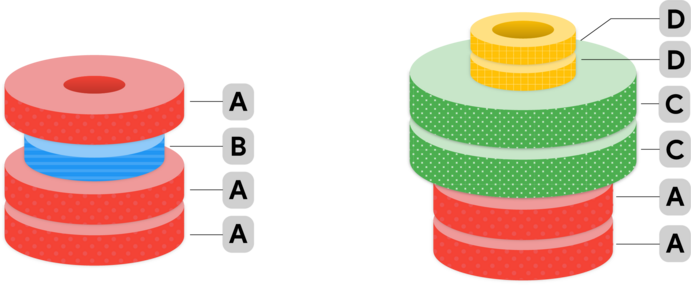
The weights are placed on the machine as a stack. Formally, with a single operation, you can either add a new weight of any type to the top of the stack, or remove the weight that is currently at the top of the stack.
You can load the weights for each exercise onto the machine's stack in any order. So, if you place the weight of type B at the bottom in the first exercise of the example above, you will have to take all the weights off before putting on the weights for the second exercise. On the other hand, if you place the weight of type B third from the bottom, you can leave two of the weights of type A on the bottom of the stack to be part of the next exercise's set, saving you some time.
Given the amount of weights of each type needed for each exercise, find the minimum number of operations needed to do them all. You must complete the exercises in the order given. The machine stack starts out empty, and you must leave it empty after you finish with all your exercises.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow. Each test case starts with a line containing $$$2$$$ integers $$$\mathbf{E}$$$ and $$$\mathbf{W}$$$: the number of exercises and the number of types of weights. Weight types are numbered between $$$1$$$ and $$$\mathbf{W}$$$. Then, $$$\mathbf{E}$$$ lines follow. The $$$i$$$-th of these lines contains $$$\mathbf{W}$$$ integers $$$\mathbf{X_{i,1}}, \mathbf{X_{i,2}}, \dots, \mathbf{X_{i,W}}$$$ representing that the $$$i$$$-th exercise requires exactly $$$\mathbf{X_{i,j}}$$$ weights of type $$$j$$$.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$,
where $$$x$$$ is the test case number (starting from 1) and $$$y$$$ is the minimum number of
machine stack operations needed to run through all your exercises.
Limits
Time limit: 20 seconds.
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$1 \le \mathbf{X_{i,1}} + \mathbf{X_{i,2}} + \dots + \mathbf{X_{i,W}}$$$, for all $$$i$$$. (Each exercise requires at least one weight.)
Test Set 1 (Visible Verdict)
$$$1 \le \mathbf{E} \le 10$$$.
$$$1 \le \mathbf{W} \le 3$$$.
$$$0 \le \mathbf{X_{i,j}} \le 3$$$, for all $$$i, j$$$.
Test Set 2 (Hidden Verdict)
$$$1 \le \mathbf{E} \le 100$$$.
$$$1 \le \mathbf{W} \le 100$$$.
$$$0 \le \mathbf{X_{i,j}} \le 100$$$, for all $$$i, j$$$.
Sample
3 3 1 1 2 1 2 3 1 2 1 2 1 2 3 3 3 1 1 3 3 3 2 3 3
Case #1: 4 Case #2: 12 Case #3: 20
In Sample Case #1, there is only one type of weight. The first exercise needs $$$1$$$ weight, the second needs $$$2$$$ weights, and the third needs $$$1$$$ weight. You can complete the exercise in $$$4$$$ operations as follows:
- Add a weight onto the stack. You do the first exercise.
- Add a weight onto the stack. You do the second exercise.
- Remove a weight from the top of the stack. You do the third exercise.
- Remove a weight from the top of the stack. Now the stack becomes empty.
In Sample Case #2, one way to complete the exercises in $$$12$$$ operations is as follows:
- Add a weight of type $$$2$$$.
- Add a weight of type $$$3$$$.
- Add a weight of type $$$1$$$.
- Add a weight of type $$$2$$$. Now the stack contains weights of types $$$2, 3, 1, 2$$$ from bottom to top. You do the first exercise.
- Remove a weight of type $$$2$$$ from the top of the stack.
- Add a weight of type $$$3$$$.
- Add a weight of type $$$1$$$. Now the stack contains weights of types $$$2, 3, 1, 3, 1$$$ from bottom to top. You do the second exercise.
- Remove a weight of type $$$1$$$ from the top of the stack.
- Remove a weight of type $$$3$$$ from the top of the stack.
- Remove a weight of type $$$1$$$ from the top of the stack.
- Remove a weight of type $$$3$$$ from the top of the stack.
- Remove a weight of type $$$2$$$ from the top of the stack. Now the stack becomes empty.
Analysis — A. Double or One Thing
For any string $$$\mathbf{S}$$$, the number of new strings we can obtain from it is at most $$$2^{|\mathbf{S}|}$$$ because for each character in $$$\mathbf{S}$$$, there are $$$2$$$ choices: to highlight it or not.
Test Set 1
Since the length of $$$\mathbf{S}$$$ is at most $$$10$$$, the number of new strings we can obtain is at most $$$2^{10}$$$. We can enumerate all of them to find the lexicographically smallest one. The time complexity of this solution is $$$O(2^{|\mathbf{S}|}\times|\mathbf{S}|)$$$ because there are $$$2^{|\mathbf{S}|}$$$ strings in total to compare, and the length of them is at most $$$2\times |\mathbf{S}|$$$.
Test Set 2
Now that the length of $$$\mathbf{S}$$$ can be up to $$$100$$$, $$$2^{100}$$$ is too large to enumerate all of them.
Note that a string $$$p$$$ appears before a different string $$$q$$$ in alphabetical order if $$$p$$$ is a prefix of $$$q$$$ or if $$$p$$$ has a letter lexicographically smaller at the leftmost position at which $$$p$$$ and $$$q$$$ differ.
Then, for any character $$$\mathbf{S_i}$$$ in $$$\mathbf{S}$$$, we have the following rule to decide whether to highlight it or not:
- If the next different character in $$$\mathbf{S}$$$ is lexicographically larger than the current character (in other words, there is an index $$$j$$$ that $$$\mathbf{S_j}\gt \mathbf{S_i}$$$ and $$$\mathbf{S_k} = \mathbf{S_i}$$$ for all $$$i \lt k \lt j$$$), then we must highlight $$$\mathbf{S_i}$$$. That is because when we double $$$\mathbf{S_i}$$$, we also push $$$\mathbf{S_j}$$$ right and replace that index with $$$\mathbf{S_i}$$$ at the same time. Therefore doubling $$$\mathbf{S_i}$$$ will make the new string lexicographically smaller.
- If the next different character in $$$\mathbf{S}$$$ is lexicographically smaller than the current character (in other words, there is an index $$$j$$$ that $$$\mathbf{S_j}\lt \mathbf{S_i}$$$ and $$$\mathbf{S_k} = \mathbf{S_i}$$$ for all $$$i \lt k \lt j$$$), then we must NOT highlight $$$\mathbf{S_i}$$$. That is because when we double $$$\mathbf{S_i}$$$, we also push $$$\mathbf{S_j}$$$ right and replace that index with $$$\mathbf{S_i}$$$ at the same time. Therefore doubling $$$\mathbf{S_i}$$$ will make the new string lexicographically larger.
- If there is no next characters different from $$$\mathbf{S_i}$$$ (in other words, $$$i$$$ is the last index in $$$\mathbf{S}$$$ or $$$\mathbf{S_k} = \mathbf{S_i}$$$ for all $$$i \lt k \lt |\mathbf{S}|$$$), then we must NOT highlight $$$\mathbf{S_i}$$$. That is because doubling $$$\mathbf{S_i}$$$ will make the original string be the prefix of the new string, which means the new string is lexicographically larger.
There are a lot of different ways to implement it and here is one: We can preprocess the given $$$\mathbf{S}$$$
into groups of same and continuous characters. For example, BOOKKEEPER is
preprocessed as [(B,1), (O,2), (K,2), (E,2), (P,1), (E,1), (R,1)]. Then for each
element in this list, we output the character with twice its original occurrence if the character
of the next element is lexicographically larger than it. Otherwise, we output the character with
its original occurrence.
The time complexity of this solution is $$$O(|\mathbf{S}|)$$$ because we need to iterate through $$$\mathbf{S}$$$ when preprocessing it, and iterate through the preprocessed list with length up to $$$|\mathbf{S}|$$$ when outputing the final answer.
Analysis — B. Equal Sum
In this problem we first pick half of the input, then the judge picks the other half, and then we need to solve an NP-complete problem on that input. This means we have to be really strategic on how we pick that input.
We only get to provide half of the numbers. So, it might be best to first see how good of a split we can do with using just the judge provided numbers and only afterwards come up with the numbers we provide.
A common heuristic to solve problems in which we do not know all of the input yet is to optimize locally. In this case, sort out the numbers into two sets, trying for their sums to be as close as possible. That means, we go through the input integers and assign them to the set that has the smallest current sum. After we process all of the judge's integers, this guarantees that the difference between the sets is bounded by the size of a single integer ($$$10^9$$$), as opposed to being bounded by the total sum of the integers we have seen ($$$10^{11}$$$).
We need our integers to always be able to make up for that difference, so we need to guarantee at least some of the integers we pick are big enough. Moreover, we need to be able to make up for the difference exactly, so we want to pick integers that get progressively more precise. This smells like binary. However, when writing in binary we get to sum over a subset of the powers of $$$2$$$. In this case, the integers that do not end up in one subset go to the other one, so binary can just write any possible difference. That being said, powers of $$$2$$$ still work, as long as we do not write in binary.
After we finish sorting out the judge's input, we know that the difference between the two subsets is at most $$$10^9$$$. Therefore, if we decide where to put the largest power of $$$2$$$ ($$$2^{29}$$$) using the same algorithm, that guarantees that the difference is now at most $$$2^{29}$$$. As long as the next number is always at least half of the previous one, we can maintain the difference bounded by the last processed number. If we process the powers of $$$2$$$ last, and in decreasing order, the difference between the two subsets at the end is no larger than $$$2^0 = 1$$$. Since the limits guarantee that the total sum is even, the difference is $$$0$$$.
The paragraph above shows that any set of integers up to $$$X$$$ with even sum that contains every power of $$$2$$$ no greater than $$$X$$$ can be partitioned into two subsets of equal sum. Moreover, the partition can be found efficiently. There are $$$30$$$ powers of $$$2$$$ between $$$1$$$ and $$$10^9$$$, which means we can choose the other $$$70$$$ integers we are entitled in any way.
Analysis — C. Weightlifting
Test Set 1
The limits for Test Set 1 are small enough that we can afford to use brute force. Since there is no reason to have more than $$$\max_j \mathbf{X_{i,j}}$$$ weights of type $$$i$$$, the number of possible states of the stack to consider is very limited (in fact, it is $$$\sum_{0 \le a,b,c \le 3} \frac{(a+b+c)!}{a!b!c!} = 5248$$$). To solve for the minimum number of operations to finish all of the exercises, you can use a breadth-first search over all possible combinations of the stack states and the number of completed exercises. Specifically, the breadth-first search starts at the state of an empty stack with no completeted exercises, and the final answer is the distance from that to the state where the stack is empty but all exercises are completed.
Test Set 2
The first observation we can make to solve Test Set 2 of this problem is the following: if there are any weights that are used in every exercise, it is always optimal to put them at the bottom of the stack before the first exercise, and leave them there until after the last one. Moreover, if there are multiple such weights, putting them in any order is equivalent. Formally, if $$$C$$$ is the multiset of weights that is common to all exercises, there is an optimal solution that has $$$C$$$ at the bottom of the stack during all exercises.
Now, for a given full sequence of exercises, let us call $$$A$$$ to the largest sequence of weights that appears at the bottom of the stack for all exercises ($$$A$$$ could be empty). Since $$$A$$$ is used for all exercises, $$$A \subseteq C$$$. If we use the first observation, then also $$$C \subseteq A$$$, so $$$A = C$$$. Therefore, we can make a second observation: if there is more than one exercise, there is at least one time in between exercises in which the stack contains exactly $$$C$$$. This points towards a divide and conquer solution: find that intermediate point and then recursively solve the problem of minimizing the operations before and after that point, disregarding $$$C$$$.
As it is common with divide and conquer approaches, we can either find the place to split without recursion, or we can use memoization to be able to simply try every possible split point, without incurring significant additional computation time.
To formalize the approach, let $$$C(\ell,r)$$$ be the multiset of weights that is the intersection of the multiset of weights needed for each exercise between $$$\ell$$$ and $$$r$$$, inclusive. Additionally, let $$$M(\ell, r)$$$ be the minimum number of operations to get from a stack containing $$$C(\ell,r)$$$, in any order, perform all operations between $$$\ell$$$ and $$$r$$$, inclusive, and leave the stack with $$$C(\ell, r)$$$ on it, in the same order. To calculate $$$M(\ell, r)$$$ we follow the strategy above: for some mid-point $$$x$$$ we do this twice: load the additional weights for one part of the split, optimize according to a recursive result, then unload those additional weights. The additional weights for the left part of the split are $$$C(\ell, x) \setminus C(\ell, r)$$$ and for the right part of the split are $$$C(x+1, r) \setminus C(\ell, r)$$$ (notice that $$$C(\ell, r)$$$ is included in the other two multisets by definition). Therefore, the cost in addition to the recursion for the mid-point $$$x$$$ is $$$2 \times (|C(\ell, x)| + |C(x+1, r)| - 2 \times |C(\ell, r)|)$$$. Putting it all together:
- $$$M(\ell, r) = 0$$$, if $$$\ell = r$$$;
- $$$M(\ell, r) = \min_{\ell \le x \lt r} \bigl(M(\ell, x) + M(x+1, r) + 2 \times (|C(\ell, x)| + |C(x+1, r)| - 2 \times |C(\ell, r)|)\bigr)$$$, otherwise.
Precomputing the $$$O(\mathbf{E}^2)$$$ values of $$$C$$$ takes $$$O(\mathbf{E}^2 \times \mathbf{W})$$$ time. With memoization, we can compute the $$$O(\mathbf{E}^2)$$$ values $$$M$$$ in $$$O(\mathbf{E}^3)$$$ overall time. This is fast enough to pass Test Set 2.