Google Code Jam Archive — Round 1C 2021 problems
Overview
The final of the Round 1s of 2021, Round 1C, was quite laborious. The first problem, Closest Picks, was all about carefully picking your bets to maximize your odds. It could be solved with a combination of simple probabilities and a greedy strategy. Roaring Years took us on a history refresher course, but besides the playful reference, it was all about properly splitting the space into disjoint cases, and a solution followed straightforwardly from that. Finally, Double or NOTing looked like a classical application of graph algorithms. However, to get the full points you had to go a different route and think carefully about binary representations.
The first perfect score took just over an hour, which was longer than both of the other Round 1s. This gave nqiiii first place in the round. daltao and square1001 came in second and third place, respectively. Ultimately, 71 coders managed a perfect score. Around 8000 coders submitted solutions in today's contest. The unofficial cutoff to advance to Round 2 is 54 points.
This wraps up our Round 1s for the year. We'll finalize the results in the coming days. In the meantime, you can keep improving your skills by practicing on this round's or any past round's problems in the archive.
If you placed in the top 1500, we will see you again in about 2 weeks as you join 3000 participants coming from the other Round 1s to compete in Round 2. Don't forget to check your local time in the schedule page. If you didn't earn enough points to advance, we hope you had a wonderful time with our first 14 problems of the year. You are invited to follow along for the rest of the season, and we hope to see you again next year!
Cast
Closest Pick: Written by Pablo Heiber. Prepared by Timothy Buzzelli.
Roaring Years: Written by Ian Tullis. Prepared by Artem Iglikov.
Double or NOTing: Written by Ian Tullis. Prepared by Artem Iglikov.
Solutions and other problem preparation and review by Abhishek Singh, Andy Huang, Artem Iglikov, Darcy Best, Ian Tullis, Liang Bai, Max Ward, Md Mahbubul Hasan, Nafis Sadique, Pablo Heiber, Sadia Atique, Swapnil Gupta, Timothy Buzzelli, and Yui Hosaka.
Analysis authors:
- Closest Pick: Pablo Heiber.
- Roaring Years: Pablo Heiber.
- Double or NOTing: Artem Iglikov.
A. Closest Pick
Problem
You are entering a raffle for a lifetime supply of pancakes. $$$\mathbf{N}$$$ tickets have already been sold. Each ticket contains a single integer between $$$1$$$ and $$$\mathbf{K}$$$, inclusive. Different tickets are allowed to contain the same integer. You know exactly which numbers are on all of the tickets already sold and would like to maximize your odds of winning by purchasing two tickets (possibly with the same integer on them). You are allowed to choose which integers between $$$1$$$ and $$$\mathbf{K}$$$, inclusive, are on the two tickets.
You know you are the last customer, so after you purchase your tickets, no more tickets will be purchased. Then, an integer $$$c$$$ between $$$1$$$ and $$$\mathbf{K}$$$, inclusive, is chosen uniformly at random. If one of your tickets is strictly closer to $$$c$$$ than all other tickets or if both of your tickets are the same distance to $$$c$$$ and strictly closer than all other tickets, then you win the raffle. Otherwise, you do not win the raffle.
Given the integers on the $$$\mathbf{N}$$$ tickets purchased so far, what is the maximum probability of winning the raffle you can achieve by choosing the integers on your two tickets optimally?
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow. Each test case consists of two lines. The first line of a test case contains two integers $$$\mathbf{N}$$$ and $$$\mathbf{K}$$$: the number of tickets already sold and the limit of the range of integers to pick from, respectively. The second line contains $$$\mathbf{N}$$$ integers $$$\mathbf{P_1}, \mathbf{P_2}, \dots, \mathbf{P_N}$$$, representing the integers on the tickets that have already been purchased.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$,
where $$$x$$$ is the test case number (starting from 1) and
$$$y$$$ is the maximum win probability you can achieve if you choose your tickets
optimally.
$$$y$$$ will be considered correct if it is within an
absolute or relative error of $$$10^{-6}$$$ of the correct answer. See the
FAQ
for an explanation of what that means, and what formats of real numbers
we accept.
Limits
Time limit: 10 seconds.
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
$$$1 \le \mathbf{N} \le 30$$$.
$$$1 \le \mathbf{P_i} \le \mathbf{K}$$$, for all $$$i$$$.
Test Set 1 (Visible Verdict)
$$$1 \le \mathbf{K} \le 30$$$.
Test Set 2 (Visible Verdict)
$$$1 \le \mathbf{K} \le 10^9$$$.
Sample
4 3 10 1 3 7 4 10 4 1 7 3 4 3 1 2 3 2 4 4 1 2 4 2
Case #1: 0.5 Case #2: 0.4 Case #3: 0.0 Case #4: 0.25
In Sample Case #1, you can purchase tickets with the integers $$$4$$$ and $$$8$$$ on them and then win if $$$4, 5, 8, 9$$$, or $$$10$$$ are chosen giving you $$$5/10 = 0.5$$$ probability of winning. Purchasing tickets with the integers $$$6$$$ and $$$8$$$ on them also yields a $$$0.5$$$ probability of winning, but no combination yields more.
In Sample Case #2, $$$6$$$ and $$$8$$$ is a possible optimal pair of tickets, which wins when $$$c$$$ is one of $$$6, 8, 9$$$, or $$$10$$$. Note that the integers on the tickets are not necessarily given in sorted order.
In Sample Case #3, every possible $$$c$$$ is at distance $$$0$$$ from an already purchased ticket, so you cannot win regardless of your choices.
In Sample Case #4, if you pick $$$3$$$ for at least one of your tickets, you win on $$$c = 3$$$, for $$$1/4 = 0.25$$$ win probability. There is no way to win when $$$c$$$ is any other integer, so that is the best you can do.
B. Roaring Years
Problem
Something is happening in $$$2021$$$ that has not happened in over a century. $$$2021$$$, like $$$1920$$$ before it, is a roaring year. A year represented by a positive integer $$$y$$$ is roaring if the decimal writing (without leading zeroes) of $$$y$$$ is the concatenation of the decimal writing (without leading zeroes) of two or more distinct consecutive positive integers, in increasing order. In this case, $$$2021$$$ is a roaring year because it is the concatenation of $$$20$$$ and $$$21$$$.
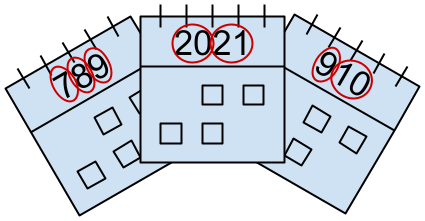
Three calendars from roaring years, marked to show how roaring their years are.
Other examples of roaring years are $$$12$$$, $$$789$$$, $$$910$$$, $$$1234$$$, and $$$9899100$$$. $$$2020$$$ was not roaring because the only list of two or more positive integers that concatenate into $$$2020$$$ is $$$[20, 20]$$$, and it is not made of consecutive integers. Similarly, there are only three lists for $$$2019$$$: $$$[20, 1, 9]$$$, $$$[201, 9]$$$, and $$$[20, 19]$$$. The first two are not made of consecutive integers, while the third does not have the integers in increasing order. Thus, $$$2019$$$ was also not roaring. As a final example, $$$778$$$ was not a roaring year because $$$[7, 78]$$$ and $$$[77, 8]$$$ are not made up of consecutive integers and $$$[7, 7, 8]$$$ is not made up of distinct integers.
Given the current year (which may or may not be roaring), find what the next roaring year is going to be.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ lines follow. Each line represents a test case and contains a single integer $$$\mathbf{Y}$$$, the current year.
Output
For each test case, output one line containing Case #$$$x$$$: $$$z$$$,
where $$$x$$$ is the test case number (starting from 1) and $$$z$$$ is the first
year strictly after $$$\mathbf{Y}$$$ that is roaring.
Limits
Time limit: 30 seconds.
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
Test Set 1 (Visible Verdict)
$$$1 \le \mathbf{Y} \le 10^6$$$.
Test Set 2 (Hidden Verdict)
$$$1 \le \mathbf{Y} \le 10^{18}$$$.
Sample
4 2020 2021 68000 101
Case #1: 2021 Case #2: 2122 Case #3: 78910 Case #4: 123
Notice in the last Sample Case that $$$102$$$ is not a roaring year because $$$[10, 2]$$$ is not a list of consecutive integers and you cannot write $$$2$$$ with a leading zero to use $$$[1, 02]$$$.
C. Double or NOTing
Problem
You are given a starting non-negative integer $$$\mathbf{S}$$$ and an ending non-negative integer $$$\mathbf{E}$$$. Both $$$\mathbf{S}$$$ and $$$\mathbf{E}$$$ are given by their binary representation (that is, they are given written in base $$$2$$$). Your goal is to transform $$$\mathbf{S}$$$ into $$$\mathbf{E}$$$. The following two operations are available to you:
- Double your current value.
- Take the bitwise NOT of your current value. The binary representation of your current value is taken without unnecessary leading zeroes, and any unnecessary leading zeroes produced by the operation are dropped. (The only necessary leading zero is the one in the representation of $$$0$$$).
For example, by using the double operation, $$$6$$$ becomes $$$12$$$, $$$0$$$ becomes $$$0$$$, and $$$10$$$ becomes $$$20$$$. By using the NOT operation, $$$0$$$ becomes $$$1$$$, $$$1$$$ becomes $$$0$$$, $$$3 = 11_2$$$ becomes $$$0$$$, $$$14=1110_2$$$ becomes $$$1$$$, $$$10=1010_2$$$ becomes $$$5=101_2$$$, and $$$5=101_2$$$ becomes $$$2=10_2$$$. ($$$X_2$$$ means the integer whose binary representation is $$$X$$$).
You can use these operations as many times as you want in any order. For example, you can transform $$$\mathbf{S} = 10001_2$$$ to $$$\mathbf{E} = 111_2$$$ using the NOT operation first, then using the double operation twice, and then another NOT operation: $$$$10001_2 \overset{\text{NOT}}{\Longrightarrow} 1110_2 \overset{\times 2}{\Longrightarrow} 11100_2 \overset{\times 2}{\Longrightarrow} 111000_2 \overset{\text{NOT}}{\Longrightarrow} 111_2.$$$$
Determine the smallest number of operations needed to complete the transformation, or say it is impossible to do so.
Input
The first line of the input gives the number of test cases, $$$\mathbf{T}$$$. $$$\mathbf{T}$$$ test cases follow. Each consists of a single line containing two strings $$$\mathbf{S}$$$ and $$$\mathbf{E}$$$, the binary representations of the starting and ending integers, respectively.
Output
For each test case, output one line containing Case #$$$x$$$: $$$y$$$, where $$$x$$$
is the test case number (starting from 1) and $$$y$$$ is IMPOSSIBLE
if there is no way to transform $$$\mathbf{S}$$$ into $$$\mathbf{E}$$$ using the two operations. Otherwise, $$$y$$$
is the smallest number of operations needed to transform $$$\mathbf{S}$$$ into $$$\mathbf{E}$$$.
Limits
Time limit: 10 seconds.
Memory limit: 1 GB.
$$$1 \le \mathbf{T} \le 100$$$.
Each character of $$$\mathbf{S}$$$ is either 0 or 1.
The first digit of $$$\mathbf{S}$$$ can be 0 only if the length of $$$\mathbf{S}$$$ is $$$1$$$.
Each character of $$$\mathbf{E}$$$ is either 0 or 1.
The first digit of $$$\mathbf{E}$$$ can be 0 only if the length of $$$\mathbf{E}$$$ is $$$1$$$.
Test Set 1 (Visible Verdict)
$$$1 \le$$$ the length of $$$\mathbf{S} \le 8$$$.
$$$1 \le$$$ the length of $$$\mathbf{E} \le 8$$$.
Test Set 2 (Hidden Verdict)
$$$1 \le$$$ the length of $$$\mathbf{S} \le 100$$$.
$$$1 \le$$$ the length of $$$\mathbf{E} \le 100$$$.
Sample
6 10001 111 1011 111 1010 1011 0 1 0 101 1101011 1101011
Case #1: 4 Case #2: 3 Case #3: 2 Case #4: 1 Case #5: IMPOSSIBLE Case #6: 0
Sample Case #1 is the example shown in the main part of the statement.
These are possible optimal ways of solving Sample Cases #2, #3, and #4, respectively: $$$$1011_2 \overset{\text{NOT}}{\Longrightarrow} 100_2 \overset{\times 2}{\Longrightarrow} 1000_2 \overset{\text{NOT}}{\Longrightarrow} 111_2,$$$$ $$$$1010_2 \overset{\times 2}{\Longrightarrow} 10100_2 \overset{\text{NOT}}{\Longrightarrow} 1011_2, \text{ and}$$$$ $$$$0_2 \overset{\text{NOT}}{\Longrightarrow} 1_2.$$$$
In Sample Case #5, it is not possible to get from $$$0_2$$$ to $$$101_2$$$ with any sequence of operations.
In Sample Case #6, we do not need to perform any operations because $$$\mathbf{S} = \mathbf{E}$$$.
Analysis — A. Closest Pick
Test Set 1
In Test Set 1, the limits are small enough that we can try every one of the $$$\mathbf{K}^2$$$ possible pairs of integers to pick. For each of those, we can calculate the probability of winning with each possible draw. There are $$$\mathbf{K}$$$ possible values for $$$c$$$. If for each one, we check the distance to each $$$\mathbf{P_i}$$$ and to our own two picks, we end up with an overall running time of $$$O(\mathbf{K}^3 \cdot \mathbf{N})$$$. This is fast enough to pass.
There are several possible optimizations. A simple one is to search for the "closest picked integer" using a sorted structure, reducing that phase to $$$O(\log \mathbf{N})$$$ and the overall running time to $$$O(\mathbf{K}^2 \cdot \mathbf{N} \log \mathbf{N})$$$. It is also possible to search for the distance from each $$$c$$$ to each $$$\mathbf{P_i}$$$ only once, independently of our choices, which reduces the overall running time further to $$$O(\mathbf{K}^2)$$$.
Test Set 2
For Test Set 2, we can optimize all phases from the previous solution. If every integer is already picked at least once, then the answer is always $$$0$$$ as the samples demonstrate. Otherwise, we can divide the non-purchased integers from $$${1, 2, ..., \mathbf{K}}$$$ into intervals between $$$\mathbf{P_i}$$$s. For example, if the $$$\mathbf{P_i}$$$ values are $$$3, 4, 8, 3$$$ and $$$\mathbf{K}=8$$$, the intervals would be $$$[1, 2], [5, 7]$$$.
If we make only one of our picks within one of those intervals, we can get closest to all of it if the interval contains $$$1$$$ or $$$\mathbf{K}$$$, by picking ours next to the only delimiting $$$\mathbf{P_i}$$$ (picking $$$2$$$ from $$$[1, 2]$$$ in the example above). If the interval is surrounded by two $$$\mathbf{P_i}$$$s, we can get closest to at most half of the integers in the interval (rounding up), which is achievable by picking either end (picking either $$$5$$$ or $$$7$$$ from $$$[5, 7]$$$). If we make both of our picks within one of those intervals, we can get closest to all integers in the interval by picking both ends ($$$5$$$ and $$$7$$$ from $$$[5, 7]$$$).
This shows that only integers that are next to an already purchased integer are worth picking for ourselves. At this point, we can go back to our last Test Set 1 solution and do the same but restricting our picks to integers next to a $$$\mathbf{P_i}$$$, which makes the $$$\mathbf{K}$$$s in the running time be $$$O(\mathbf{N})$$$, making it fast enough with the right implementation.
A few extra reasoning steps lead to a much more efficient solution. There are only $$$O(\mathbf{N})$$$ ways to make both picks within the same interval, and we can check each of them. If we choose two different intervals, it is always optimal to choose the two most valuable ones, so we do not need to check each combination separately. This leads to a single additional case that requires $$$O(\mathbf{N})$$$ time to compute to find the top two intervals. All in all, this solution takes only linear time (after sorting the array to find the intervals). This solution requires some care about corner cases, specifically the cases when no or just one integer from $$$[1, \mathbf{K}]$$$ is not a $$$\mathbf{P_i}$$$, and the case of the intervals list containing a single interval.
Analysis — B. Roaring Years
Test Set 1
A straightforward approach
Notice that $$$1234567$$$ is a roaring year that happens after every possible input. That means that if we simply check every year after $$$\mathbf{Y}$$$ to see if it is roaring or not, we need to check no more than $$$1234567$$$ years per case. It is a lot less in practice, but that is also harder to prove.
To check whether a year $$$y$$$ is roaring, we can check for each prefix $$$p$$$ of $$$y$$$ whether "completing it" by appending $$$p+1$$$, $$$p+2$$$, etc., would work. Since only prefixes that are at most half the length of $$$y$$$ can work, this is a small number of things to check. If we are unconvinced about the running time, we can simply run a check of roaringness for every integer up to $$$1234567$$$ once initially and remember it, after which each test case is simply looking for the next "true" in a rather small table, making the running time mostly independent of the actual input, so a test run can help convince us that it will run in time without risking penalty with a real submission.
An approach with a more clear time complexity
Another way to go is to first use the observation at the end of the solution above: the length of the first number in the concatenation is small — at most 3 digits. We can try each of the $$$999$$$ possibilities and concatenate numbers to it until it goes above the $$$1234567$$$ threshold. Notice that this is at most $$$6$$$. This builds a set of all possible roaring years that matter in very little time. After that, we can use linear search in this very small list (less than $$$6000$$$ elements) to find the smallest roaring year that is larger than $$$\mathbf{Y}$$$ for each test case. Of course, we could use binary search to make each test case run even faster, but that is not required.
Test Set 2
None of the approaches above work for Test Set 2. The gap between two consecutive roaring years can easily be large (for example, you can prove as an exercise that there are no other roaring years between $$$100000000100000001$$$ and $$$100000001100000002$$$) and checking an individual one, while quick, takes a bit more time than before. For the second approach, there are now $$$10^9-1$$$ candidates for the first number in the concatenation, and the amount of concatenated numbers can also be much larger for some of those, making the full set of roaring years too big to even fit in memory, not to mention the computation time.
A case-based approach
The last sentence of the previous paragraph hints at an idea. While the full set of roaring years in range is too big, the full set of roaring years that are the concatenation of $$$3$$$ or more numbers is not: for that case, the maximum possible starting number has $$$6$$$ digits. We can use the second Test Set 2 solution with this change to solve for those. We still need to check roaring years that are the concatenation of exactly two consecutive numbers. Notice that $$$f(x) = $$$ the concatenation of $$$x$$$ and $$$x+1$$$ is an increasing function. Therefore, we can use the bisection method to efficiently find the minimum of that subset of roaring years that is above $$$\mathbf{Y}$$$. After we found the best candidate from each subset, we simply return the smallest of them.
A general approach
We can also generalize the second case of our first approach for Test Set 2. The family of functions $$$f_n(x) = $$$ concatenation of $$$x, x+1, \dots, x+n-1$$$ are all increasing. We can therefore use bisection to find the best candidate for each possible amount of consecutive numbers $$$n$$$, and then answer the best of those. Since $$$n$$$ is at most $$$\log \mathbf{Y}$$$ this yields a method that runs in $$$O(\log^2 \mathbf{Y})$$$ time, which means it can work for really large bounds.
Analysis — C. Double or NOTing
Test Set 1
Let's construct a graph where the nodes are numbers and the edges are the operations described in the statement. The problem asks us to find the shortest path from node $$$\mathbf{S}$$$ to node $$$\mathbf{E}$$$ in this graph. The graph is infinite, but we can inspect only a limited set of nodes to find the answer.
When thinking about binary representations, the double operation can be described as "add a trailing zero". Note that it is never optimal to add more zeroes than we have bits in $$$\mathbf{E}$$$: because the NOT operation can only drop leading digits, any additional zeroes will ultimately have to be dropped anyway.
We can use this fact to limit the maximal length to the sum of the lengths of $$$\mathbf{S}$$$ and $$$\mathbf{E}$$$, and then use a Breadth-first search algorithm to find the shortest path.
Test Set 2
Let's define a bit group as a maximally long group of consecutive zeroes or consecutive ones (that is, a group of all bits $$$b$$$ that does not have a $$$b$$$ adjacent to it). Let's assume that there are $$$K$$$ bit groups in $$$\mathbf{S}$$$ and $$$L$$$ bit groups in $$$\mathbf{E}$$$.
The double operation appends a bit to the right end of the binary string, and the NOT operation complements and possibly drops bits from the left end. Therefore, the result of applying operations to $$$\mathbf{S}$$$ comes from some (possibly empty) suffix of $$$\mathbf{S}$$$ (possibly complemented) and then some extra bits that were created using double. Let us call the bits that come from a bit in $$$\mathbf{S}$$$ reused.
First, let's consider the case when we do not reuse any bits from $$$\mathbf{S}$$$. In such a case we need to construct $$$\mathbf{E}$$$ naively using only the bits added by double operations and removing all the bits that came from $$$\mathbf{S}$$$ originally. We can do this by adding zeroes with double operations and applying a NOT operation whenever we need to start a new bit group. We also need to apply additional NOT operations to eliminate all bits that came from $$$\mathbf{S}$$$ originally. If we end up with $$$\mathbf{E}$$$, then let's count this as a possible answer. For example, to get from 1012 to 111002 we would need to do perform the following sequence of operations (we use a space to separate bits originated from $$$\mathbf{S}$$$ from the extra bits added with double operations):
| Operation | Result |
|---|---|
| double (to add an extra bit) | 101 0 |
| double (to add an extra bit) | 101 00 |
| double (to add an extra bit) | 101 000 |
| NOT (because the length of first bit group in $$$\mathbf{E}$$$ is 3, and we have added 3 zeros already, now we need to start a new bit group) | 10 111 |
| double (to add an extra bit) | 10 1110 |
| double (to add an extra bit) | 10 11100 |
| NOT (because we already have the desired $$$\mathbf{E}$$$ as suffix, now we just need to remove extra bits from $$$\mathbf{S}$$$) | 1 00011 |
| NOT (to remove the leftover bit of $$$\mathbf{S}$$$) | 11100 |
If $$$\mathbf{S}$$$ ends in $$$0$$$, we need to perform an extra NOT operation at the beginning so that our first double operation creates a brand new bit group. After we finish removing all bits from $$$\mathbf{S}$$$, we might need another NOT operation, if the removal process left us with the complement of $$$\mathbf{E}$$$.
Now, let's try to reuse some bits from $$$\mathbf{S}$$$.
The NOT operation removes one bit group from the left end of the binary representation and complements the rest. It is never optimal to apply a NOT operation more than $$$K + 1$$$ times, as in such a case we will either be looping between $$$0$$$ and $$$1$$$, or will be removing bits which were added with the double operation (which we could have just not added in the first place if they were not useful).
Let's assume that the answer will have NOT operations applied exactly $$$X$$$ times. Let's apply $$$X$$$ NOT operations to $$$\mathbf{S}$$$ to obtain $$$S'$$$. If $$$S'$$$ is not a prefix of $$$\mathbf{E}$$$, then it is not possible to get to $$$\mathbf{E}$$$ from $$$\mathbf{S}$$$ using $$$X$$$ NOT operations, as the double operation will not change the prefix of the string.
If $$$S'$$$ is a prefix of $$$\mathbf{E}$$$, let's see whether we can construct the suffix. We will need exactly $$$Y = \text{len}(\mathbf{E}) - \text{len}(S')$$$ double operations. Let's say there are $$$M$$$ bit groups in the suffix we need to create, then we will also need to apply $$$M$$$ or $$$M + 1$$$ NOT operations, depending on the parity of $$$M$$$ and the first bit of the prefix. Let's denote the number as $$$Z$$$. If $$$Z$$$ is greater than $$$X$$$, then this case does not work, as we would apply more than $$$X$$$ NOT operations, violating the assumption. Otherwise, the answer is $$$X + Y$$$, as even if $$$X$$$ is greater than $$$Z$$$, extra NOT operations won't affect the suffix (we can perform them before adding any extra bits with a double operation).
We can now iterate through all possible values of $$$X$$$ from $$$0$$$ to $$$K + 1$$$, inclusive,
and choose the minimum answer between all of those and the non-reuse case we considered first.
If none of the cases work, we output IMPOSSIBLE.