Google Code Jam Archive — Round 1A 2020 problems
Overview
Round 1A was the second of three weekend contests in a row! This time, we opened with Pattern Matching, which was not as difficult as it may have initially seemed. Pascal Walk was an ad hoc problem that could be solved via various graph searching strategies, or with a more "mathy" insight. Square Dance required some thought about data structures. We hope there was something for everyone!
Benq took a lead early on by solving the first and last problems in under 20 minutes, but then our six-time defending champion Gennady.Korotkevich snagged first place with a perfect score only 33 minutes and 19 seconds into the round! Next up was vepifanov at 43:01, followed by ecnerwala, semiexp., and Geothermal.
Almost 12000 contestants submitted attempts in this round! Pattern Matching got a lot of solves, but Pascal Walk was tougher, and many contestants never made it to Square Dance. Even so, there were over 400 perfect scores! The tentative cutoff for advancement to Round 2 from this round (top 1500) is 63 points, plus a fast enough penalty time; that corresponds to solving the first two problems.
As usual, we will aim to finalize the results well before next weekend's Round 1B. If you advanced in this round, you can relax until Round 2 in mid-May, but if not, you have two more chances coming up! Either way, consider practicing with some past problems from our archive.
Cast
Pattern Matching: Written by Pablo Heiber. Prepared by Mohamed Yosri Ahmed, Jonathan Irvin Gunawan, and Ian Tullis.
Pascal Walk: Written by Ian Tullis. Prepared by Artem Iglikov.
Square Dance: Written by Pablo Heiber. Prepared by Yossi Matsumoto.
Solutions and other problem preparation and review by Mohamed Yosri Ahmed, Liang Bai, Timothy Buzzelli, Kevin Gu, Jonathan Irvin Gunawan, Md Mahbubul Hasan, and Artem Iglikov.
Analysis authors:
- Pattern Matching: Pablo Heiber
- Pascal Walk: Ian Tullis
- Square Dance: Artem Iglikov
A. Pattern Matching
Problem
Many terminals use asterisks (*) to signify "any string",
including the empty string. For example, when listing files matching
BASH*, a terminal may list BASH,
BASHER and BASHFUL. For *FUL, it may
list BEAUTIFUL, AWFUL and BASHFUL.
When listing B*L, BASHFUL, BEAUTIFUL
and BULL may be listed.
In this problem, formally, a pattern is a string consisting of only
uppercase English letters and asterisks (*), and a name
is a string consisting of only uppercase English letters. A pattern p
matches a name m if there is a way of replacing every asterisk in
p with a (possibly empty) string to obtain m. Notice that each
asterisk may be replaced by a different string.
Given N patterns, can you find a single name of at most 104 letters that matches all those patterns at once, or report that it cannot be done?
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case starts with a line with a single integer N: the number of patterns to simultaneously match. Then, N lines follow, each one containing a single string Pi representing the i-th pattern.
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1) and y
is any name containing at most 104 letters such that each
Pi matches y according to the definition
above, or * (i.e., just an asterisk) if there is no such name.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 100.
2 ≤ N ≤ 50.
2 ≤ length of Pi ≤ 100, for all i.
Each character of Pi is either an uppercase English letter
or an asterisk (*), for all i.
At least one character of Pi is an uppercase English
letter, for all i.
Test set 1 (Visible Verdict)
Exactly one character of Pi is an asterisk
(*), for all i.
The leftmost character of Pi is the only asterisk
(*), for all i.
Test set 2 (Visible Verdict)
Exactly one character of Pi is an asterisk
(*), for all i.
Test set 3 (Visible Verdict)
At least one character of Pi is an asterisk
(*), for all i.
Sample
2 5 *CONUTS *COCONUTS *OCONUTS *CONUTS *S 2 *XZ *XYZ
Case #1: COCONUTS Case #2: *
In Sample Case #1, there are other possible answers, including
COCOCONUTS and ILIKECOCONUTS.
Neither COCONUTSAREGREAT nor COCOANUTS would be
acceptable. Notice that the same pattern may appear more than once within a
test case.
In Sample Case #2, there is no acceptable name, so the answer is
*.
The following cases could not appear in Test Set 1, but could appear in Test Set 2 or Test Set 3:
4 H*O HELLO* *HELLO HE*
HELLO and HELLOGOODBYEHELLO are examples of
acceptable answers. OTHELLO and HELLOO would not be
acceptable.
2 CO*DE J*AM
There is no name that matches both patterns, so the answer would be
*.
2 CODE* *JAM
CODEJAM is one example of an acceptable answer.
The following cases could not appear in Test Set 1 or Test Set 2, but could appear in Test Set 3:
2 A*C*E *B*D*
ABCDE and ABUNDANCE are among the possible
acceptable answers, but BOLDFACE is not.
2 A*C*E *B*D
There is no name that matches both patterns, so the answer would be
*.
2 **Q** *A*
QUAIL and AQ are among the possible acceptable
answers here.
B. Pascal Walk
Problem
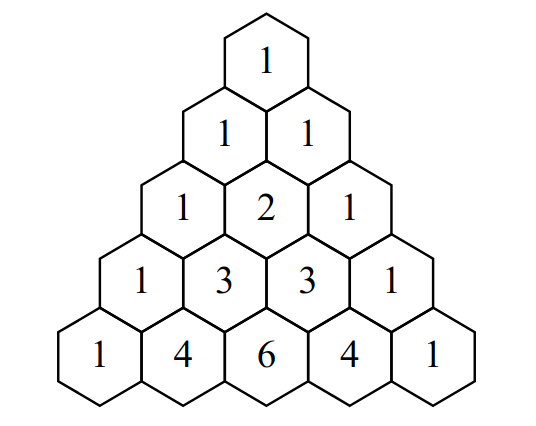
Pascal's triangle consists of an infinite number of rows of an increasing number of integers each, arranged in a triangular shape.
Let us define (r, k) as the k-th position from the left in the r-th row, with both r and k counted starting from 1. Then Pascal's triangle is defined by the following rules:
- The r-th row contains r positions (r, 1), (r, 2), ..., (r, r).
- The numbers at positions (r, 1) and (r, r) are 1, for all r.
- The number at position (r, k) is the sum of the numbers at positions (r - 1, k - 1) and (r - 1, k), for all k with 2 ≤ k ≤ r - 1.
The first 5 rows of Pascal's triangle look like this:
In this problem, a Pascal walk is a sequence of s positions (r1, k1), (r2, k2), ..., (rs, ks) in Pascal's triangle that satisfy the following criteria:
- r1 = 1 and k1 = 1.
- Each subsequent position must be within the triangle and adjacent (in one of the six possible directions) to the previous position. That is, for all i ≥ 1, (ri + 1, ki + 1) must be one of the following that is within the triangle: (ri - 1, ki - 1), (ri - 1, ki), (ri, ki - 1), (ri, ki + 1), (ri + 1, ki), (ri + 1, ki + 1).
- No position may be repeated within the sequence. That is, for every i ≠ j, either ri ≠ rj or ki ≠ kj, or both.
Find any Pascal walk of S ≤ 500 positions such that the sum of the numbers in all of the positions it visits is equal to N. It is guaranteed that at least one such walk exists for every N.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each consists of a single line containing a single integer N.
Output
For each test case, first output a line containing Case #x:,
where x is the test case number (starting from 1). Then, output
your proposed Pascal walk of length S ≤ 500 using S additional lines. The i-th of
these lines must be ri ki where
(ri, ki) is the i-th position in the walk. For example, the first line
should be 1 1 since the first position for all valid walks is (1, 1).
The sum of the numbers at the S positions of your proposed Pascal walk must be exactly N.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 100.
Test set 1 (Visible Verdict)
1 ≤ N ≤ 501.
Test set 2 (Visible Verdict)
1 ≤ N ≤ 1000.
Test set 3 (Hidden Verdict)
1 ≤ N ≤ 109.
Sample
3 1 4 19
Case #1: 1 1 Case #2: 1 1 2 1 2 2 3 3 Case #3: 1 1 2 2 3 2 4 3 5 3 5 2 4 1 3 1
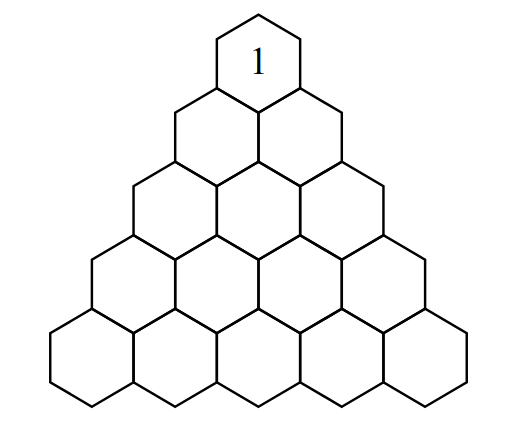
In Sample Case #1, only the starting position is needed.
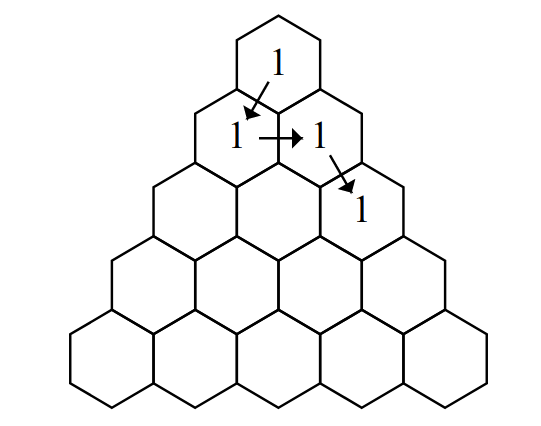
In Sample Case #2, notice that although a shorter path exists, the path does not need to be of minimal length, as long as it uses no more than 500 positions.
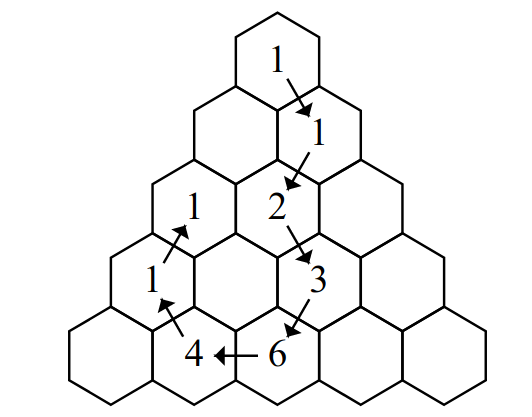
The following image depicts our solution to Sample Case #3:
C. Square Dance
Problem
You are organizing an international dancing competition. You have already obtained all of the following:
- A dance floor with R rows and C columns, consisting of unit square cells;
- R × C competitors;
- A cutting-edge automated judge for the competition.
But you are still missing an audience! You are worried that the competition might not be interesting enough, so you have come up with a way to calculate the interest level for the competition.
Each competitor occupies one square unit cell of the floor and stays there until they are eliminated. A compass neighbor of a competitor x is another competitor y chosen such that y shares a row or column with x, and there are no competitors still standing in cells in between x and y. Each competitor may have between 0 and 4 compass neighbors, inclusive, and the number may decrease if all the other competitors in one orthogonal direction are eliminated.
The competition runs one round at a time. In between rounds i and i+1, if a competitor d had at least one compass neighbor during round i, and d's skill level is strictly less than the average skill level of all of d's compass neighbors, d is eliminated and is not part of the competition for rounds i+1, i+2, i+3, etc. Notice that d still counts as a neighbor of their other compass neighbors for the purpose of other eliminations that may also happen between rounds i and i+1. Competitors that do not have any compass neighbors are never eliminated. If after a round no competitor is eliminated, then the competition ends.
The interest level of a round is the sum of skill levels of the competitors dancing in that round (even any competitors that are to be eliminated between that round and the next). The interest level of the competition is the sum of the interest levels of all of the rounds.
Given the skill levels of the dancers that are on the floor for the first round, what is the interest level of the competition?
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case begins with a line containing two integers R and C. Then, there are R more lines containing C integers each. The j-th value on the i-th of these lines, Si, j, represents the skill level of the dancer in the cell in the i-th row and j-th column of the floor.
Output
For each test case, output one line containing
Case #x: y,
where x is the test case number (starting from 1) and
y is the interest level of the competition.
Limits
Time limit: 40 seconds per test set.
Memory limit: 1GB.
1 ≤ Si,j ≤ 106, for all i and j.
Test set 1 (Visible Verdict)
1 ≤ T ≤ 100.
1 ≤ R × C ≤ 100.
Test set 2 (Hidden Verdict)
10 ≤ T ≤ 100.
1000 < R × C ≤ 105, in exactly 10 cases.
1 ≤ R × C ≤ 1000, in exactly T - 10 cases.
Sample
4 1 1 15 3 3 1 1 1 1 2 1 1 1 1 1 3 3 1 2 1 3 1 2 3
Case #1: 15 Case #2: 16 Case #3: 14 Case #4: 14
In Sample Case #1, only one competitor is on the floor. Since the competitor does not have any compass neighbors, they dance in one round, and then the competition is over. Thus the answer is equal to the dancer's skill level, 15.
In Sample Case #2, the interest level of the first round is 1+1+1+1+2+1+1+1+1=10.
The competitors that are not in the center nor in a corner have a skill level of 1, but the average of their compass neighbors is 4 / 3, which is greater than 1, so they are eliminated. The floor during the second round looks like this:
1 . 1 . 2 . 1 . 1
This round is the last one. The competitors in the corner have two compass neighbors each, but the average of their skill level is equal to their own. The competitor in the center has no compass neighbor. The interest level of the round is 1+1+2+1+1=6. This means the interest level of the competition is 10+6=16.
In Sample Case #3, the competitor with skill level 1 is eliminated after the first round, while the other two remain. In the second round, the two other competitors become compass neighbors, and this causes the competitor with skill level 2 to be eliminated. There is a single competitor in the third round, which makes it the last one. The interest levels of the rounds are 6, 5 and 3, making the interest level of the competition 14.
Analysis — A. Pattern Matching
Test Set 1
In Test Set 1, each pattern forces our answer to have a certain suffix, and we first need to check whether the patterns introduce conflicting requirements for that suffix.
Consider the letter strings coming after the initial asterisk in each pattern. We can find the longest of those strings (or any longest, if there is a tie); call that string L. Then at least one answer exists if (and only if) every other string is a suffix of L; note that we are considering L itself to be a suffix of L. We can check each other string against L by starting at the ends of both strings and stepping backwards through them in tandem until we find a discrepancy or run out of letters to check. If we ever find a discrepancy, then the case has no answer, but otherwise, we know that L itself is an acceptable answer.
Test Set 2
In Test Set 2, we can divide the patterns into (1) patterns that start with an asterisk, (2) patterns that end with an asterisk, and (3) patterns with an asterisk in the middle.
A type (1) pattern requires the output word to have a certain suffix, just as in Test Set 1. A type (2) pattern requires the output word to have a certain prefix. A type (3) pattern introduces both of these requirements, and we can split it into a suffix requirement and a prefix requirement, and then handle those separately.
Then, we can apply our strategy from Test Set 1 twice: once for the prefix constraints (with the algorithm modified to compare prefixes instead), and once for the suffix constraints. We can concatenate the two results together to obtain a valid answer that is certainly short enough (since it can be at most 99+99 characters long).
Test Set 3
We can generalize the idea above into a solution for Test Set 3. Each pattern p in Test Set 3 also prescribes a prefix of the output word (the prefix of p up to the first asterisk) and a suffix of the output word (the suffix of p starting after the last asterisk). If we allow empty prefixes and suffixes, we get exactly one of each for every pattern. We can handle those in the same way we did for Test Set 2, ending up with a prefix P and a suffix S for the output as long as we do not find a discrepancy in either phase.
However, for patterns that have more than one asterisk, we can also have a
middle part, which imposes a new type of requirement. Suppose we parse the
parts between the asterisks of a pattern so that X is the prefix up to the
first asterisk, Y is the suffix after the last asterisk, and
M1, M2, ..., Mk are the strings in between
the asterisks, in order. After checking that X is a prefix of P and Y is a
suffix of S, as before, all that remains to ensure is that the pattern
M1*M2*...*Mk is present somewhere within the output word, strictly between P and S.
Let us call M1M2...Mk — that is, the word that occurs in between the first and last asterisks with any other asterisk removed — the middle word. If we make sure a pattern's middle word occurs in the output word outside of P and S, then we fulfill the extra requirement. We can then build a full valid output then by starting with P, then adding the middle word of every pattern in any order, then appending S. We make sure to correctly handle words with a single asterisk or only consecutive asterisks by making their middle words the empty string. Since each middle word contains at most 98 characters, and the prefix and suffix contain at most 99 characters each, the output built this way has at most 99 × 2 + 50 × 98 characters, which is within the limit of 104.
Analysis — B. Pascal Walk
Test set 1
The answer for N ≤ 500 can always be constructed by walking along the leftmost positions of the rows of the triangle: (1, 1), (2, 1), ..., (N-1, 1), (N, 1).
We can handle the case N = 501 by making a detour to pick up the 2 in the third row before returning to the left side. That is, our walk takes us through the positions (1, 1), (2, 2), (3, 3), (3, 2), (3, 1), (4, 1), ..., (498, 1).
Test set 2
With only 1000 possible test cases to consider, we can find an answer to each one before submitting. One way to do this is to walk over the triangle in e.g. a breadth-first or random way, taking care never to reuse a position or visit more than 500 positions. We can check our cumulative sum at each position, and whenever we encounter a sum that we have never seen before, we record the sequence of positions that we used to obtain it. When our sum exceeds 1000, we backtrack in our search or start over with a new random path, and so on, until we have an answer for every possible N. It's difficult to prove a priori that this will work, but we can be optimistic given that the top few rows of the triangle have many small values to work with. Indeed, this method finds a full set of solutions very quickly.
An alternate method is to observe that the positions immediately to the right of the leftmost positions — named (x, 2) for each x ≥ 2 — are 1, 2, 3, 4, 5, and so on. We can move from the top position in the triangle down to the 1 at position (2, 1), then follow that line to the 2 at (3, 2), the 3 at (4, 3), etc., until our next move would cause the cumulative sum to exceed our target. Then, we can instead make a move to the left to reach a 1 on the left edge of the triangle, and then proceed downward along that edge, taking as many extra 1s as we need. Since the sum of the first 45 natural numbers is over 1000, we can be sure that we will never need to take more than 45 of these extra 1s, or visit more than 45 of the positions along this line of natural numbers. This ensures we never use more than 90 positions in total.
Test set 3
There are various ways to solve the third test set, but one of our favorites takes advantage of a special property of Pascal's triangle: the entries in the r-th row (counting starting from 1) sum to 2r-1. This is to be expected from the way in which each row is constructed from the previous one: each element in a row contributes to two elements in the next row, so the sum doubles with each row.
This observation suggests a strategy for constructing any N that we want: write N in binary, and then look through that representation, starting from the least significant bit. If the r-th least significant bit (counting starting from 1) is a 1, our path should consume all of the elements in the r-th row. If the r-th least significant bit is a 0, we should skip that row somehow. We only need the first 30 rows of the triangle, since the 31st row's sum is 230, which is larger than the maximum possible N of 109. Even if we used every element in these first 30 rows (which we would never need to), that would only use 465 positions, which is within the limit of 500.
This doesn't quite work as written, though, because our path must be continuous, and so there is no way to skip a row. But we can get close via the following variant: proceed down one side of the triangle (that is, the diagonal line of 1s) as long as we keep encountering 0 bits. Whenever we encounter a 1 bit, we send our path horizontally across the corresponding row, sending us to the other side of the triangle. This almost gets us the number we want, but we probably overshoot because we have consumed some extra 1s from the rows corresponding to 0 bits. We can be sure that there are fewer than 30 of those, though, since we visit at most 30 rows.
So, we can use that variant, but instead of constructing N, we construct N-30 instead. Once we finish, we can tack on additional 1s from our current edge of the triangle until we reach N. (We can handle cases with N ≤ 30 specially, and just go down one edge of the triangle.)
There are other less elaborate ways to solve this test set, though! One is to walk down the centers of the rows (e.g., going from (1, 1) to (2, 1) to (3, 2) to (4, 2) to (5, 3)...). This is where the largest numbers live, so we will grow our sum as rapidly as possible. At some point, though, when moving downward would make our sum grow too much, we can instead move to a one step away from the center and continue zigzagging downward, and so on. Eventually we will reach the edge full of 1s, and we can take as many more as we need. We must be careful not to increase the sum so fast that we will not be able to "escape" to the edge of 1s. Nor should we reach the edge too early, since we can only take so many 1s. However, it's not too difficult to get this method to work.
Analysis — C. Square Dance
Test Set 1
Test Set 1 can be solved by simulating the competition:
-
Iterate through all the cells of the floor. For each cell, if there is a dancer in that cell:
- Add their level to the interest level of the competition.
- Loop through their row and column to find all of their compass neighbors.
- Count the number of their compass neighbors, and sum up their levels.
- If the average level of the neighbors (calculated as sum of their levels divided by how many neighbors there are) is greater than the level of the current dancer, add this dancer to an elimination list.
- Go through the elimination list and eliminate the dancers.
- If the elimination list is empty, we are done. Otherwise, start again from step 1.
Each iteration of the above algorithm has a time complexity of O(R×C×(R + C)), and there are as many iterations as there are rounds in the competition. The number of rounds in a competition cannot be larger than the total number of dancers, R × C. So the total time complexity is O(R2×C2×(R + C)).
Test Set 2
Let's optimize our Test Set 1 solution — specifically, the following parts of it:
- For each round, we iterate through all R×C cells and check whether each dancer is eliminated.
- For each dancer, we may have to iterate through a significant part of their row and column in order to find their compass neighbors.
To improve the situation described in the first point above, we can observe that for i > 1, if dancer d is not eliminated in round i-1 and they are eliminated in round i, their set of compass neighbors must have changed in between. For that to have happened, at least one compass neighbor of d must have been eliminated in round i-1.
Using this observation, instead of checking every dancer in round i, we can limit the check to the compass neighbors of those eliminated in round i-1. Since a dancer has at most 4 compass neighbors at the time of elimination, the length of the list of candidates to check in round i is at most 4 times the length of the elimination list for round i-1. The sum of the lengths of all elimination lists is at most R × C; therefore, the sum of the lengths of all lists of candidates to check is at most 4 × R × C. With the initial check of all dancers, this means that we do O(R × C) checks overall with this improvement.
To optimize finding compass neighbors, notice that when we remove a dancer, their eastern neighbor becomes the eastern neighbor of their western neighbor and vice versa. The same thing happens to the southern and northern neighbors. So, instead of finding the neighbors each time we need them, we can maintain the specific location of the neighbor in each direction for each dancer, and update their locations in constant time whenever we eliminate one. This is effectively like keeping a linked list to represent each row and column, and this structure allows us to remove and find neighbors in constant time.
Since we do O(R × C) checks thanks to the first optimization, and each check can be done in constant time thanks to the second optimization, this yields an O(R × C) time algorithm that solves the problem fast enough for Test Set 2.