Google Code Jam Archive — World Finals 2016 problems
Overview
Our 2016 final round featured five problems instead of the typical six, but they were a bit tougher on average than usual, and they were sufficient to keep all of our contestants busy. Nobody solved all five, but each of the five was solved at least once.
Integeregex was a relatively approachable but implementation-heavy problem involving regular expressions and automata. Family Hotel and Gallery of Pillars were challenging combinatorics and math/geometry problems, respectively. Map Reduce was a graph problem that required some tough but satisfying insights, and Radioactive Islands was an unusual path optimization exercise that allowed several possible approaches.
kevinsogo jumped out to an impressive early lead with A, B, and C in just over two hours. About 45 minutes after that, defending champion Gennady.Korotkevich started to turn up the heat with an impressive flurry of solving that included D, C-small, and B-large. Throughout most of the last hour, there were several opportunities for another contestant to pass Gennady.Korotkevich, but he pulled out of reach in the last 10 minutes with the first and only complete solution to E. This left him just one dataset (C-large) shy of a perfect score, and he took the championship for the third year in a row!
kevinsogo and EgorKulikov spent some time grappling with D and C, respectively, but ultimately attained impressive scores of 120 and took the honors of second and third place. semiexp. and rng..58 also distinguished themselves as the first solvers of problems B and C, respectively. (EgorKulikov was the first to solve A, and Gennady.Korotkevich had the first solutions for D and E.)
That wraps up our 2016 season! We hope you enjoyed participating, and we'll be back again next year to serve up another selection of challenging and fun problems!
You can enjoy a detailed writeup of each problem in the following tabs, but additionally, you can check out the part of the livestream in which two of the Code Jam engineers provide a quick explanation of the problems here.
Cast
Problem A (Integeregex): Written by Pablo Heiber. Prepared by Alex Li, Seth Troisi, and Ian Tullis.
Problem B (Family Hotel): Written and prepared by Petr Mitrichev.
Problem C (Gallery of Pillars): Written by David Arthur. Prepared by Pablo Heiber.
Problem D (Map Reduce): Written by David Arthur and Pablo Heiber. Prepared by Pablo Heiber and Alex Li.
Problem E (Radioactive Islands): Written by John Dethridge. Prepared by John Dethridge and Igor Naverniouk.
Solutions and other problem preparation and review by Shane Carr, John Dethridge, Andy Huang, Alex Li, Alex Meed, Petr Mitrichev, Onufry Wojtaszczyk, Karol Pokorski, and Ian Tullis.Analysis authors:
- Integeregex: Seth Troisi
- Family Hotel: Mohammad Hossein Bateni
- Gallery of Pillars: Pablo Heiber
- Map Reduce: David Arthur and Alex Meed
- Radioactive Islands: John Dethridge, Igor Naverniouk, and Ian Tullis
Pictures in statements and analyses by Brian Hirashiki.
A. Integeregex
Problem
In this problem, a valid regular expression is one of the following. In the following descriptions, E1, E2, etc. denote (not necessarily different) valid regular expressions.
- A decimal digit: that is, one of
0 1 2 3 4 5 6 7 8 9. - Concatenation: E1E2.
- Disjunction:
(E1|E2|...|EN), for at least two expressions. Note that the outer parentheses are required. - Repetition:
(E1)*. Note that the outer parentheses are required.
For example, 7, 23, (7)*,
(45)*, (1|2|3), ((2)*|3),
(1|2|3), and ((0|1))* are valid expressions.
(7), 4|5, 4*, (1|), and
(0|1)* are not.
We say that an expression E matches a string of digits D if and only if at least one of the following is true:
- E = D.
- E = E1E2 and there exist D1 and D2 such that D = D1D2 and Ei matches Di.
- E =
(E1|E2|...|EN)and at least one of the Ei matches D. - E =
(E1)*and there exist D1, D2, ..., DN for some non-negative integer N such that D = D1D2...DN and E1 matches each of the Di. In particular, note that(E1)*matches the empty string.
For example, the expression ((1|2))*3 matches 3,
13, 123, and 2221123, among other
strings. However, it does not match 1234,
3123, 12, or 33, among other strings.
Given a valid regular expression R, for how many integers between A and B, inclusive, does R match the integer's base 10 representation (with no leading zeroes)?
Input
The first line of the input gives the number of test cases, T. T
test cases follow; each consists of two lines. The first line has two positive
integers A and B: the inclusive limits of the integer range we
are interested in. The second has a string R consisting only of
characters in the set 0123456789()|*, which is guaranteed to be a
valid regular expression as described in the statement above.
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1) and y is
the number of integers in the inclusive range [A, B] that the
the regular expression R matches.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1 GB.
1 ≤ T ≤ 100.
1 ≤ A ≤ B ≤ 1018.
1 ≤ length of R ≤ 30.
Small dataset (Test Set 1 - Visible)
R contains no | characters.
Large dataset (Test Set 2 - Hidden)
No additional limits.
Sample
8 1 1000 (0)*1(0)* 379009 379009 379009 1 10000 (12)*(34)* 4 5 45 1 100 ((0|1))* 1 50 (01|23|45|67|23) 1 1000000000000000000 ((0|1|2|3|4|5|6|7|8|9))* 1 1000 1(56|(((7|8))*9)*)
Case #1: 4 Case #2: 1 Case #3: 5 Case #4: 0 Case #5: 4 Case #6: 2 Case #7: 1000000000000000000 Case #8: 6
Note that sample cases 5 through 8 would not appear in the Small dataset.
In sample case 1, the matches in range are 1, 10, 100, and 1000.
In sample case 2, the match in range is 379009.
In sample case 3, the matches in range are 12, 34, 1212, 1234, and 3434.
In sample case 4, there are no matches in range.
In sample case 5, the matches in range are 1, 10, 11, and 100.
In sample case 6, the matches in range are 23 and 45.
In sample case 7, it is possible to form any number in the range.
In sample case 8, the matches in range are 1, 19, 156, 179, 189, and 199.
B. Family Hotel
Family Hotel
You run a hotel with N rooms arranged along one long corridor, numbered from 1 to N along that corridor. Your guests are big families, and every family asks for exactly two adjacent rooms when they arrive. Two rooms are adjacent if their numbers differ by exactly 1.
At the start of the day today, your hotel was empty. You have been using the following simple strategy to assign rooms to your guests. As each family arrives, you consider all possible pairs of adjacent rooms that are both free, pick one of those pairs uniformly at random, and assign the two rooms in that pair to the family. New families constantly arrive, one family at a time, but once there are no more pairs of adjacent rooms that are both free, you turn on the NO VACANCY sign and you do not give out any more rooms.
Given a specific room number, what is the probability that it will be occupied at the time that you turn on the NO VACANCY sign?
Input
The first line of the input gives the number of test cases, T. T lines follow. Each line contains two numbers: the number of rooms N and the room number K that we are interested in.
Output
For each test case, output one line containing Case #x: y, where x is
the test case number (starting from 1) and y is the sought probability computed
modulo 109+7, which is defined precisely as follows.
Represent the probability that room K is occupied as an irreducible fraction
p/q. The number y then must satisfy the modular equation
y × q ≡ p (mod 109+7), and be between 0 and
109+6, inclusive. It can be shown that under the constraints of this problem such a
number y always exists and is uniquely determined.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1 GB.
1 ≤ T ≤ 100.
1 ≤ K ≤ N.
Small dataset (Test Set 1 - Visible)
2 ≤ N ≤ 104.
Large dataset (Test Set 2 - Hidden)
2 ≤ N ≤ 107.
Sample
4 3 1 3 2 4 1 4 2
Case #1: 500000004 Case #2: 1 Case #3: 666666672 Case #4: 1
In sample case #3, there are four rooms and we are looking for probability that the
first room is occupied. When the first family arrives, there are 3 possible situations, each with
probability 1/3: occupy rooms 1+2, 2+3 or 3+4. In the first situation, the first room is already
occupied and will stay occupied.
In the second situation, the first room is free and no more families can be accommodated, so
it will stay free. Finally, in the third situation, the next arriving family
will definitely get rooms 1+2, and thus the first room will be occupied.
The probability that the first room is occupied
is thus 2/3, and the answer is 666666672, since
(666666672 * 3) mod 1000000007 = 2 mod 1000000007.
The probability for sample case #1 is 1/2, and for sample cases #2 and #4 it is 1.
C. Gallery of Pillars
Problem
Your friend Cody-Jamal is working on his new artistic installment called "Gallery of Pillars". The installment is to be exhibited in a square gallery of N by N meters. The gallery is divided into N2 squares of 1 by 1 meter, forming an N by N matrix. The exact center of the southwest corner cell is called the viewpoint; a person viewing the artwork is supposed to stand there. Each other cell contains a cylindrical pillar. All pillars have two circular bases of radius R: one resting on the floor, in the center of its corresponding cell, and the other touching the gallery's ceiling. The observer will stand in the viewpoint, observe the N2 - 1 pillars, and marvel.
Cody-Jamal is currently scouting venues trying to see how large he can make the value of N. Also, he has not decided which material the pillars will be made of; it could be concrete, or carbon nanotubes, so the radius R of the base of each pillar could vary from 1 micrometer to almost half a meter. Notice that a radius of half a meter would make neighboring pillars touch.
You, as a trained mathematician, quickly observe that there could be pillars impossible to see from the viewpoint. Cody-Jamal asks your help in determining, for different combinations of N and R, the number of visible pillars. Formally, a pillar is visible if and only if there is a straight line segment that runs from the center of the southwest corner cell (the viewpoint) to any point on the pillar's boundary, and does not touch or intersect any other pillar.
Input
The first line of the input gives the number of test cases, T. T lines follow. Each line describes a different test case with two integers N and R. N is the number of 1 meter square cells along either dimension of the gallery, and R is the radius of each pillar, in micrometers. Thus, R / 106 is the radius of each pillar in meters.
Output
For each test case, output one line containing Case #x: y, where x is the
test case number (starting from 1) and y is the number of pillars in the installment
that are visible from the viewpoint.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1 GB.
1 ≤ T ≤ 100.
1 ≤ R < 106 / 2.
Small dataset (Test Set 1 - Visible)
2 ≤ N ≤ 300.
Large dataset (Test Set 2 - Hidden)
2 ≤ N ≤ 109.
Sample
4 4 100000 4 300000 3 300000 100 499999
Case #1: 9 Case #2: 7 Case #3: 5 Case #4: 3
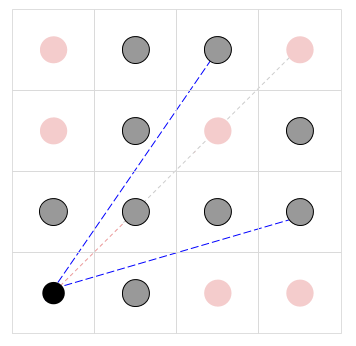
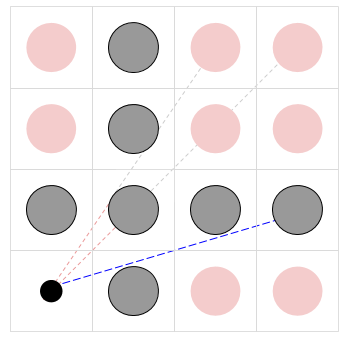
The pictures below illustrate the first two samples (not to scale). In the center of the black circle is the observer. The other circles are pillars, with the visible ones in gray and the not visible ones in red. The blue dotted lines represent some of the unblocked lines of sight; the red dotted lines represent blocked lines of sight (that turn gray at the point at which they are first blocked).
 |
 |
D. Map Reduce
Problem
Ben the brilliant video game designer is trying to design maps for his upcoming
augmented-reality mobile game. Recently, he has created a map which is
represented as a matrix of R rows and C columns. The map consists
of a bunch of . characters representing empty squares, a bunch of
# characters representing impassable walls, a single start position
represented by S and a single finish position represented by
F. For example, the map could look like:
############# #S..#..##...# ###.##..#.#F# #...##.##.### #.#.........# #############
In Ben's game, a path is a sequence of steps (up, down, left or right) to go from one cell to another while not going through any impassable walls.
Ben considers a good map to have the following properties:
- There is a path between any two empty squares (including the start and finish positions).
- To preserve structural integrity, impassable walls must meet at edges and
not just corners. For every 2×2 region in the map, if the region contains
exactly two walls, then those walls are either in the same row or the same
column. In other words, there is no 2×2 region where the walls are in one
of these two configurations:
#. .#
.# #.
- The boundary consists of only impassable walls. A cell is considered part of the boundary if it is in the uppermost/lowermost rows or if it is in the leftmost/rightmost columns.
The distance of the shortest path is the minimum number of steps required to reach the finish position from the start position. For instance, the shortest path in the above example takes 17 steps.
Being such a clever mapmaker, Ben realized that he has created a map that is too hard for his friends to solve. He would like to reduce its difficulty by removing some of the impassable walls. In particular, he wants to know whether it is possible to remove zero or more impassable walls from his map such that the shortest path from start to finish takes exactly D steps, and that the resulting map is still good. Note that it is not enough to simply find a path with D steps; D must be the number of steps in the shortest path.
For example, if D = 15, we could remove the impassable wall directly below the finish position to get a good solution.
############# #S..#..##...# ###.##..#.#F# #...##.##.#.# #.#.........# #############
There is no solution if D = 5.
Input
The first line of the input gives the number of test cases, T. T
test cases follow. Each test case starts with a line containing three
space-separated integers R, C and D: the number of rows and
columns in the map, and the desired number of steps in the shortest path from
start to finish after possibly removing impassable walls. R lines follow,
each consisting of C characters (either ., #,
S or F) representing Ben's map.
It is guaranteed that the map is good, as described in the problem statement.
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1) and y is
the word POSSIBLE or IMPOSSIBLE, depending on whether
the shortest path can be made equal to D by removing some number of walls
such that the map is still good. If it is possible, output R more lines
containing C characters each, representing the new map. In your output,
replace the # characters for removed walls (if any) with
. characters.
If multiple solutions are possible, you may output any of them.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 100.
Each test case contains exactly one S and exactly one F.
The input file is at most 3MB in size.
Small dataset (Test Set 1 - Visible)
Time limit: 60 seconds.
3 ≤ R ≤ 40.
3 ≤ C ≤ 40.
1 ≤ D ≤ 1600.
Large dataset (Test Set 2 - Hidden)
Time limit: 300 seconds.
3 ≤ R ≤ 1000.
3 ≤ C ≤ 1000.
1 ≤ D ≤ 106.
NOTE: The Large output breaks the usual cap on Code Jam output size, but you can upload it as normal.
Sample
3 6 13 15 ############# #S..#..##...# ###.##..#.#F# #...##.##.### #.#.........# ############# 5 8 3 ######## #S.....# ####...# #F.....# ######## 4 10 11 ########## #S#...#.F# #...#...## ##########
Case #1: POSSIBLE ############# #S..#..##...# ###.##..#.#F# #...##.##.#.# #.#.........# ############# Case #2: IMPOSSIBLE Case #3: POSSIBLE ########## #S#...#.F# #...#...## ##########
The sample output displays one set of answers to the sample cases. Other answers may be possible.
Sample case #1 is the example in the problem statement.
In sample case #2, it is possible to remove walls to make the distance of the shortest path either 2 or 4, for example. However, there is no way to make the distance of the shortest path exactly 3.
In sample case #3, the shortest path already takes 11 steps to begin with, so there is no need to reduce the difficulty of the map.
E. Radioactive Islands
Problem
You are steering a boat from the coordinates (-10, A) to the coordinates (10, B). The coordinates are measured in kilometers, and your boat travels at a constant speed of 1 kilometer per hour. You have full control over the path the boat takes. We model the boat as a single point.
There are N islands in the area; we model them as single points. The i-th island is at the coordinates (0, Ci).
The area is radioactive, and you constantly receive 1 microsievert per hour of radiation from the general environment, no matter where you are. Moreover, the islands themselves are radioactive, and you constantly receive additional radiation at a rate of (Di)-2 microsieverts per hour from the i-th island, where Di is your current distance (in kilometers) from the i-th island. (Formally: let Di(t) be your distance from the i-th island as a function of time t, and X be the total time your journey takes. Then the total radiation received from the i-th island is the definite integral from 0 to X of Di(t)-2.) You can get as close to an island as you would like, as long as you do not match its exact coordinates.
Find the minimum total radiation dose that you can receive if you plot your course optimally.
Input
The first line of the input gives the number of test cases, T; T test cases follow. Each test cases consists of two lines. The first line of a test case consists of three values: an integer N, and two floating-point numbers A and B, as described in the statement above. The second line of a test case consists of N floating-point numbers Ci; the i-th of these numbers gives the y coordinate of the i-th island.
All floating-point numbers are specified to exactly two decimal places.
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1) and y is
the minimum radiation dose (in microsieverts) received while completing the
journey.
y will be considered correct if it is within an absolute or
relative error of 10-3 of the correct answer. See the
FAQ for an
explanation of what that means, and what formats of real numbers we accept.
Limits
Memory limit: 1 GB.
-10.00 ≤ A ≤ 10.00.
-10.00 ≤ B ≤ 10.00.
-10.00 ≤ Ci ≤ 10.00, for all i.
Ci ≠ Cj, for all i ≠ j.
Small dataset (Test Set 1 - Visible)
Time limit: 120 seconds.
T ≤ 20;
N = 1.
Large dataset (Test Set 2 - Hidden)
Time limit: 240 seconds.
T ≤ 50;
1 ≤ N ≤ 2.
Sample
2 1 1.00 -2.00 0.00 2 0.00 0.00 3.00 -3.00
Case #1: 21.806 Case #2: 21.706
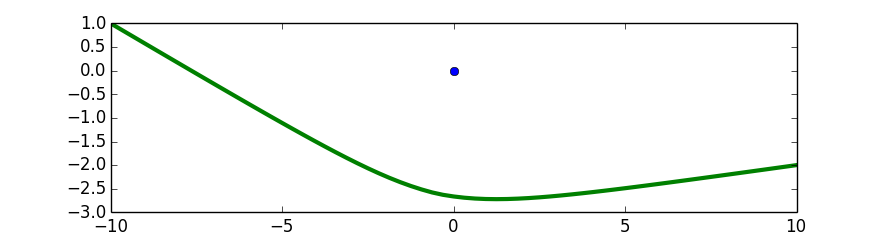
Here is a diagram of the optimal path for sample case #1. We have enlarged the island to make it more visible, but remember to treat it as a single point.
Analysis — A. Integeregex
Analysis
One handy property of regular expressions is that matching one of them is equivalent to being accepted by a special type of machine called a nondeterministic finite automaton (NFA).
An NFA is a graph of states and transitions, with a special initial and final state. Each transition is labeled with a digit or ε. When processing a string, the machine may move from a current state to another state by taking an ε-transition, or by taking a digit transition that matches the current digit of the string and moving to the next digit. After the last digit of the input string is read, only ε-transitions are allowed. If there is a path from the initial digit to the last digit that reads the entire input, we say the input string is accepted or matched, and that path is called an accepting path.
Build an NFA that matches strings to the regular expressions of the problem.
Thompson's construction is
one algorithm to construct an NFA that matches regular expressions.
The general outline is start with two special states: the initial state, q, and a
final accepting state, f.
Then build up the NFA f(E) recursively:
- If E is a digit, then f(E) contains only the two special states linked with a transition labeled with E.
- f(E = E1E2) is the union of f(E1) and f(E2), using the initial state of f(E1) as initial state of f(E), the final state of f(E2) as final state, and adding an ε-transition from the final state of f(E1) to the initial state of f(E2).
- f(E = (E1|E2|...|EN)) is the union of all the f(Ei) plus an additional initial and final state. Then, ε-transitions are added from the initial state of F(E) to each initial state of an f(Ei) and from the final state of each f(Ei) to the final state of f(E).
- f(E = (E1)*) is just f(E1) with an additional ε-transition from the final state to the initial state.
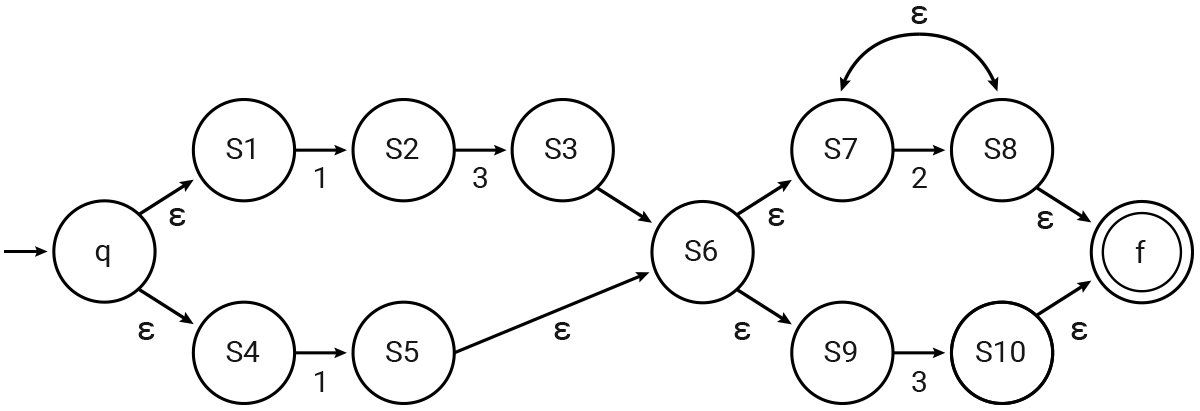
Here's an example NFA built from the Integeregex (13|1)((2)*|3)
 |
Checking that a single string matches
Consider the following example: the input string 1322 has an accepting path on the
NFA above that goes through these states:
q, s1, s2, s3, s6, s7,
s8, s7, s8, f.
Notice that there are multiple paths for each string, some may be accepting and some others may
not. Just one accepting path is enough for the string to be accepted.
Start with the set of possible states containing only the initial state (q).
For each character C in the string:
For each of the last possible states:
Find all the states that can be reached by ε-transitions then a
transition on C.
Add these to the new set of all possible states.
From the last set of possible states:
if the accepting state (f) is reached from any of these states by
ε-transitions then the NFA (and the regular expression) match!.
For example to check the string 1233 against our example NFA:
the NFA starts in the initial state q
After ε-transitions and a transition on 1, the NFA can be in any of the states
{s2, s5}.
After ε-transitions and a transition on 3, the NFA can be in any of the states
{s3, s10}.
After ε-transitions and a transition on 2, the NFA can only be state s8.
After ε-transitions and a transition on 2, the NFA can only be state s8.
Because the accepting state f can be reached from s8 with
ε-transitions, the NFA, and the regular expression, match 1322!
Quickly counting all numbers that match the NFA
We can now use dynamic programming to quickly check how many numbers less than or equal to X
match the NFA.
We keep a map of (is_empty, is_prefix_of_x, possible_states) to memoize the result starting from
that state.
We use is_empty to keep from adding zeros at the front of the number.
We use is_prefix_of_x to keep from counting numbers larger than X.
def MatchNFA(X, transitions):
x_digits = []
for c in str(X):
x_digits.append(int(c))
# Start of numbers with same length as X.
count_state = { (True, True, 'p') : 1 }
for index in range(len(X)):
# Start of shorter and shorter numbers.
new_count_state = { (True, False, 'p') : 1 }
for (is_empty, is_prefix_of_x, states), count in count_state.items():
for new_digit in range(10):
if is_empty and new_digit == 0:
continue # Numbers can't start with 0.
if is_prefix_of_x and new_digit > x_digits[index]:
continue # Numbers can't be greater than X.
# Find all possible states if new_digit was next in the string
new_possible_states = []
for start_state in states:
# Add all states that can be reached from start_state by (ε)* new_digit
for epsilon_state in transitions[start_state]['']:
new_possible_states += transitions[epsilon_state][new_digit]
new_count_state[(False, is_prefix_of_x and new_digit == x_digits[index],
set(new_possible_states))] += count
count_state = new_count_state
count_match = 0
for (is_prefix_of_x, states), count in count_state.items():
for final_state in states:
if 'f' in transitions[state]['']
count_match += count
return count_match
Finally we calculate the number of matching numbers between A and B as
MatchNFA(B, transitions) - MatchNFA(A-1, transitions).
As the number of states in the NFA grows, new_possible_states can grow exponentially
large (it can theoretically be the powerset of the states). However, the small maximum length
of the regular expression and the amount of non-digit characters consumed to include disjunctions
or repetitions make it so that the number is actually really small (for a computer) in practice.
There are mathematically provable bounds on the number, but the proofs are too long to fit
in the margins of this analysis.
Analysis — B. Family Hotel
Let P(N, K) denote the probability that room K is occupied when the NO VACANCY sign goes up. This is essentially what the problem asks for, except that it is requested in a special format. We will get to that later.
Small input
We first present an algorithm for the small input. There are N-1 ways to accommodate the first family, each with probability 1/(N-1). Suppose we assign to them adjacent rooms i and i+1. If either is equal to K, we are done. Otherwise, K falls either in the interval [1, i-1] or in the interval [i+2, N]. Take the former case without loss of generality. What happens in the interval [i+2, N] is now irrelevant. Hence the problem reduces to finding P(i-1, K). Working out the math, we get the following recurrence relation:
- P(1, 1) = 0, and
- P(N, K) = 1/(N-1) [ μ(K+1 ≤ N) + μ(K-1 ≥ 1) + ΣK+1 ≤ i ≤ N-1 P(i-1, K) + Σ1 ≤ i ≤ K-2 P(N-i-1, N-K+1) ], where 1 ≤ K ≤ N, 2 ≤ N, and μ(condition) = 1 if condition holds and 0 otherwise.
Setting aside the issues of precision and the special format requirements of the output, we can use dynamic programming to compute P(N, K) in time O(N3). This is too slow even for the small case. However, by defining S(n, k) = Σk ≤ i ≤ n P(i, k), the recurrence simplifies as follows:
P(N, K) = 1/(N-1) [ μ(K+1 ≤ N) + μ(K-1 ≥ 1) + S(N-2, K) + S(N-2, N-K+1) ].
The above recurrence can be used for an O(N2)-time algorithm, which is sufficient for the small input.
Modular arithmetic
Before proceeding to a faster solution for the large input, let us address the output format. Let M = 109+7 be the prime specified in the problem statement. For a rational solution p/q, we are asked to output the unique integer y such that 0 ≤ y < M and y*q = p (mod M). In terms of the field (ZM, +, *), we are simply looking for p/q (mod M) = p * q-1, where the latter (i.e., the inverse of q modulo M) equals qM-2 by Euler's theorem (or Fermat's little theorem). This computation requires only logarithmically many operations on integers less than M2. In fact, all the arithmetic can be carried out in this field, hence there is no need for large integers or any floating-point operations. Note that the division operation in the recurrence is well-defined since we never divide by a multiple of M.
Large input
To solve the large input, we observe the following:
Claim: P(N, K) = 1 - F(K) * F(N-K+1), where F(q) = 1-P(q, 1) denotes the probability of the left-most room being unoccupied at the end of the day.
Proof: This can be proved rigorously via induction with the base cases being when K ∈ {1, N}, and using the recurrence relation. A more elegant proof, though, is as follows. Suppose room K is left unoccupied until the end. In that case we essentially have two independent hotels, one formed with rooms from 1 to K, and the other with rooms from K to N. The first hotel gets those guests that are assigned to rooms between (1,2) and (K-1,K), and the second hotel gets those guests that are assigned to rooms between (K,K+1) and (N-1,N). It's easy to see that those two "sub-streams" of guests that are going to each hotel are also uniformly and independently distributed. The only difference between having such two hotels and one big hotel is that room K could be occupied twice in the two hotel case, but since we're considering the case where it's left unoccupied, this does not happen. Now since the two hotels are independent, we just need to multiply the probabilities that room K, which is a border room in both hotels, is left unoccupied. ■
The recurrence for P(N, K) has a simpler form for K=1, as follows:
- P(1, 1) = 0, and
- P(N, 1) = 1/(N-1) [ 1 + S(N-2, 1) ] for N ≥ 2.
Since the two one-dimensional arrays can be filled at the same time, there is an O(N)-time algorithm to compute all values of P(N, 1), hence F(N), which leads to a constant-time operation for each P(N, K) query in the input.
Final remarks
For the curious, the above recurrence yields the following solution for F(q):
F(q) = Σ0 ≤ i ≤ q-1 (-1)i 1/i!, for q ≥ 1.
This has a combinatorial meaning, as well. Consider a permutation π of 1, …, N-1, where πi denotes the time at which we try to assign pair of rooms i and i+1 (if both are vacant). Convince yourself that the number of such permutations producing a certain outcome of room assignments is proportional to that outcome's probability. Now F(q) is equal to the probability that the length of the decreasing sequence at the beginning of π be even. We calculate this via Principle of Inclusion-Exclusion.
Since the claim above is the crux of the solution for large input, it is worth noting that some contestants got the idea by simply looking at the table of 1-P(N, K) for small values of N and K.
Analysis — C. Gallery of Pillars
Gallery of Pillars: Analysis
A convenient way to look at this problem is to set up a coordinate system with the viewer at the origin and the center of every pillar at other coordinates (x,y) with x and y non-negative integers less than N.
Let us focus on a given pillar centered at (x,y). Suppose some other pillar centered at (a,b) intersects the segment [(0,0),(x,y)]. Then, (a,b) blocks at least half the view of (x,y), from the segment towards one of the sides. Then, if we consider the pillar centered at (x - a, y - b), that is, the one symmetric across the midpoint of the segment [(0,0),(x,y)], the distance from that pillar to the segment is the same, so it also covers the segment; it's located on the other side of the segment from (a,b), and so it blocks the other half of the view. It follows that the pillar centered at (x,y) is visible from the origin if and only if the segment [(0,0),(x,y)] does not intersect any other pillar. The following picture illustrates the situation.
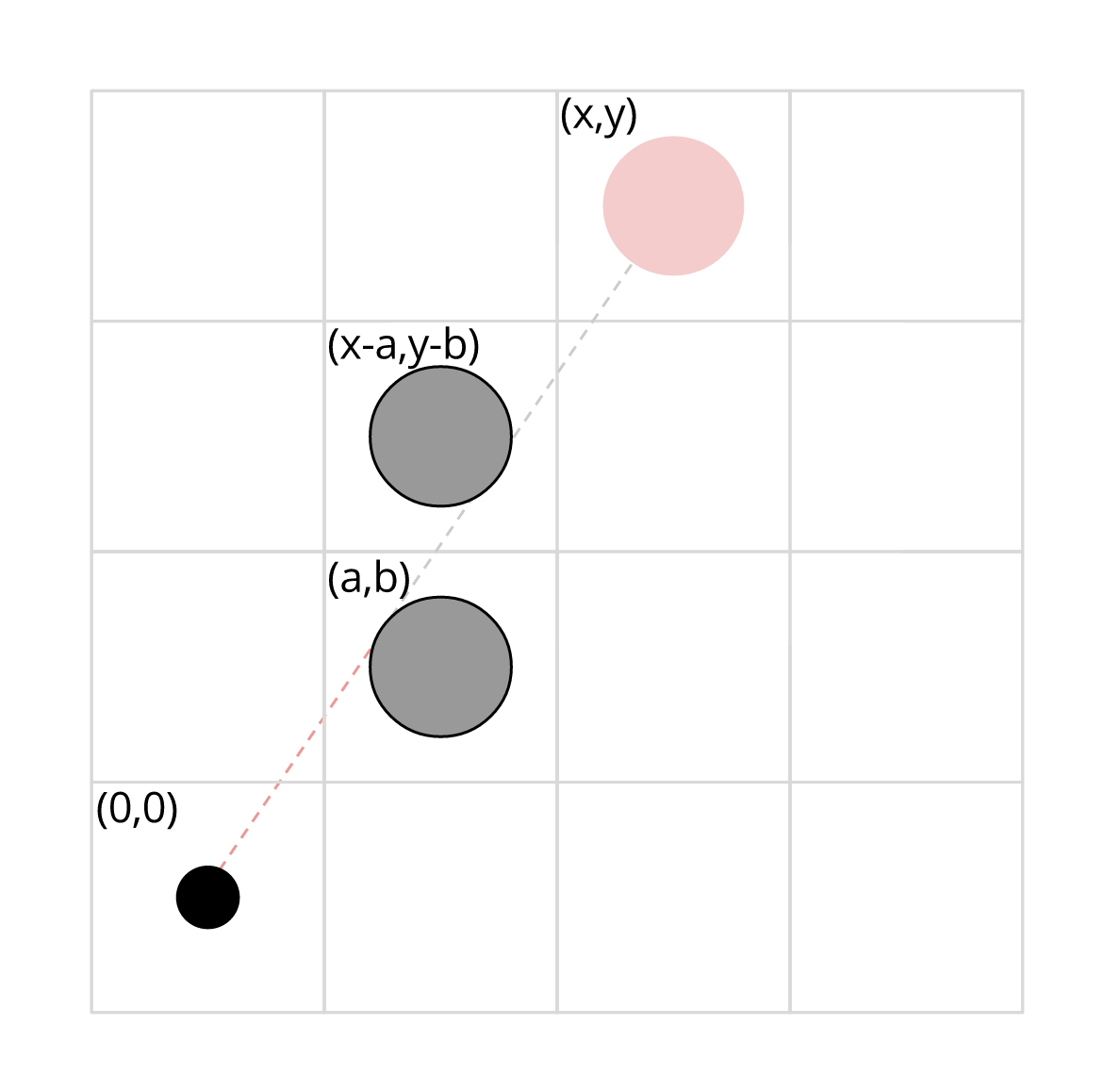
Assume the pillar centered at (a,b) intersects the segment [(0,0),(x,y)]. Clearly, a ≤ x and
b ≤ y. Moreover, the square of the
distance between the point and the segment can be expressed as
d2 = (ay - bx)2 / (x2 + y2).
Since the pillar intersects the segment, d2 × 106 ≤ R.
From this expression, we can tell in constant time whether a given pillar blocks the view of some other pillar. This immediately gives an O(N4) solution to the problem: for each pillar, check every other pillar to see whether it blocks it. This is just shy of fast enough for the Small, but there is a simple improvement: instead of checking every possible (a,b) for each (x,y), it's enough, for each possible a between 0 and x - 1, to try only b = a * y / x, rounded up and down (that is, the two points with that a coordinate that are clearly closest to the segment). This makes the complexity O(N3), which is definitely fast enough to solve the Small dataset.
The Large dataset, as usual, requires a bit more work. Let us pick up where we left off:
our expression for the squared distance
d2 = (ay - bx)2 / (x2 + y2).
If x and y are not relatively prime, choosing a = x / gcd(x,y) and b = y / gcd(x,y) yields a
pair (a,b) that fullfills every condition to cover (x,y). This is to be expected, as (a,b) clearly
covers all pillars (ka,kb) for each k > 1. If x and y are not relatively prime, then
there exist
positive a and b such that |ay - bx| = 1. Since |ay - bx| is an integer, and it can only be 0 within
our constraints when x and y are not relatively prime, choosing a pair that makes it 1 yields the
closest distance. Thus, a pillar (x,y) is visible if and only if x and y are relatively prime and
106 / (x2 + y2) < R. That is, we need to count the pairs
of relatively prime integers within a circle of radius 106 / R and a square of
size N by N.
If N ≥ 106 / R, then the square contains the circle, so let us assume further that N ≤ 106 / R ≤ 106. We can count all points inside the area, then subtract the multiples of 2, 3, 5, ..., etc, then add the multiples of 2 × 3 = 6, 2 × 5 = 10, 3 × 5 = 15, etc, that were subtracted twice, and keep doing the inclusion-exclusion argument for each possible divisor k between 1 and N. The count for points that are multiples of a given k should be multiplied by the Möbius function of k. Calculating that function for each number between 1 and N can be done efficiently with a slight modification of the sieve of Eratosthenes, which runs in linear time. For each k, we count by iterating the possible values of x, k, 2k, 3k, etc, and for each one we find the range of possible y values. We can do that by taking the minimum of N and the square root of (106 / R)2 - x2, or by binary search, or by linear search. Notice that the maximum value of y decreases from one value of x to the next, so if we pick up at the value considered for the previous x, the linear search will only take linear time overall (constant amortized time per each value of x). Linear and binary search are guaranteed to give a precise number, but using the square root also works because we are dealing with fairly small values. For the most efficient versions, the time complexity of the algorithm to get the count for a given value of k is O(N / k). Since the summation of 1 / k up to k = N can be approximated by log N, the overall complexity of the algorithm is O(N log N). Using binary search to find the range of values for y only adds a second log factor, yielding an overall O(N log2 N). Both are efficient enough for N up to 106.
Analysis — D. Map Reduce
Map Reduce: Analysis
Some initial checks
First, calculate two values: the length Li of any shortest path from the start to the finish (using BFS), and the Manhattan distance M from the start to the finish (ignoring walls). Based on those results, we can immediately detect some impossible cases:
- We can only remove walls, so we have no way to increase the length of the shortest path above Li. So, if Li is less than D, there is no solution.
- Similarly, if M is greater than D, removing walls does not help; even a blank maze consisting of only a border would still have a shortest path length > D.
- If the parity of Li and D is different, there is no solution. The lengths of all paths between any two given cells have the same parity, because each step flips the parity of the sum of the indices of the row and column.
Surprisingly, in any other case, there is always a solution. The rest of the problem is to provide a constructive proof of that fact.
A crucial observation
We want to remove walls to change the current shortest path length L to match D. The key to solving this problem is to notice that we can always remove a wall such that the new shortest path has a length of either L or L-2. The proof of this is somewhat difficult, but we can discuss it intuitively (a formal proof follows at the end of this analysis).
Consider a connected component of walls. It either includes the border or it
doesn't. Now, pick some wall W within that connected component that is as far
as possible away from either the border, or some arbitrary wall within the
component if it doesn't include the border. Using the fact that all empty
spaces are connected and that no two walls can connect at a corner, we can find
that the 3×3 neighborhood of W looks like one of the following cases,
up to symmetry (# is a wall, . is a space,
? can be either):
... ?#? ?## .W. .W. .W# ... ... ..?
Let's consider each case in turn. We will show that if the shortest path proceeded through the 3×3 neighborhood of W, removing W will decrease the length of the shortest path by at most 2:
- W has zero neighbors that are walls: The only path that would be shortened by removing W is a path that goes around W. So, removing W will shorten the path by 2, since the path can now go directly through W.
- W has one neighbor that is a wall: Say we have the case pictured above, and the shortest path proceeds from the top-left corner around the bottom to the top-right corner. Removing W again shortens the path by 2.
- W has two neighbors that are walls: Removing W doesn't shorten the path at all. (The reason we have this case is that removing this wall can open up other walls to be removed.)
Here are some illustrations of the above three cases. (For simplicity, we
assume here that all the ?s are walls, but the argument holds
regardless.)
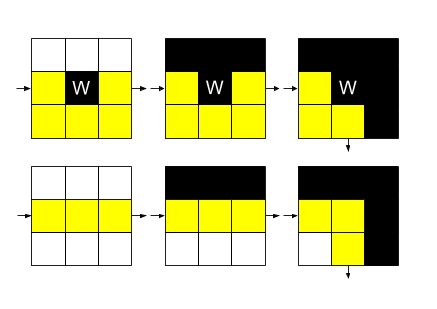
To solve the problem, then, we just continually remove walls from the map (keeping in mind that removing a wall may make another wall removable) until the shortest path is equal to D. For the Small, we can repeatedly scan the map for removable walls and remove a wall; we continue this until the shortest path is the required length.
For the Large dataset, scanning the map repeatedly is too slow, so we need a different approach. We can figure out a list of walls to remove, in order, then binary search on the number of walls to remove to make a path of the required length. To find this list, we can scan the map once, then initialize a queue containing all the removable walls. Then, each time we choose a wall to remove next, we scan each of its neighbors to see if it's removable, and add any newly-removable walls to the back of the queue. We also need to scan the neighbors for walls that may have become unremovable, and remove any such walls from the queue. For example, if a connected component is just a 2x2 square, all of its walls are initially removable, but after removing one of them, only two of the three remaining walls can be removed. So we may sometimes need to remove a wall from the queue, and then perhaps even re-insert it later.
With this method, we're only scanning the entire map once, then doing constant additional work per wall we remove (O(N) total), so it's fast enough for the Large. (This method will eventually remove every wall, except that it might leave an extra-thick unremovable border. This border doesn't matter, since removing it wouldn't change the shortest path.)
A formal proof
As before, let Li be the shortest path initially and M be the Manhattan distance. We claim that the problem is solvable for any D (of the same parity as Li) between Li and M. It suffices to show that you can always delete a wall while keeping the maze valid and without decreasing the current shortest path length L by more than 2.
Consider some connected component of walls. If it includes the outer boundary, let B be the set of walls on the outer boundary. Otherwise, let B be an arbitrary wall in the component. Let A be a wall in the component that is adjacent to an empty cell and maximally far apart from B (based on distance staying within the component). We'll delete A.
This adds an empty cell adjacent to another one, and so all empty cells stay connected. We next need to show that it can't make two walls touch only at a corner. By way of contradiction, suppose that X and Y are walls adjacent to both A and an empty cell Z. Z and A are connected by empty cells, so X and Y cannot be connected by walls after deleting A. Thus one of X or Y must be further from B than A is. But X and Y are not on the outer boundary, and are connected to B before A is deleted, and are adjacent to Z, so we have a contradiction.
Finally, we need to show that deleting A cannot make two empty cells greater than two steps closer to each other. The only way this could happen is if A were adjacent to empty opposite cells X and Y, and walls W and Z. As above, X and Y are connected, so Z and W cannot be connected by walls after deleting A. This leads to the same contradiction as before. W and Z may not be adjacent to an empty cell, but they are adjacent to something other than A that is. Either W or Z or this adjacent cell will contradict the choice of A. Note that the key claim here is false if walls are allowed to touch only at corners, but the problem setup disallows that.
Analysis — E. Radioactive Islands
Radioactive Islands: Analysis
This optimization problem touches on topics that are a bit further afield from our other problems! But a wide range of reasonable solution approaches can be successful.
We will start with some general insights, and then move on to a few of the many possible solutions.
Never get too close to an island
The radiation dose rate rises sharply as we approach an island, so any path that passes too close to an island is worse than a path that takes the time to travel around it at a greater distance away.
This is helpful because we can be more confident about numerical precision when finding approximations to the best path, since areas where the dose rate is low are also those where the derivative of the dose rate with respect to position is low.
Never move left
Although the input limits do not allow it, suppose that the boat started 0.000001 km to the left of an island. In that case, the effects of the island would be much worse than the effects of the background radiation, and we'd want to move left to "escape" from the island as fast as possible and eventually make a wide curve around it.
Also, consider a scenario where the difference in the Y-coordinates of the endpoints is large enough that the angle between them is nearly 90° from horizontal, and where there is an island in the middle of the direct path between the endpoints. Then an optimal path could start by moving almost vertically but slightly to the left, because that would give the island a wider berth without significantly increasing the total length of the path.
However, we've made the input "nice" — the boat always starts 10 km to the left of the islands, where the maximum dose rate from the islands is at most 0.02μSv/h, and the maximum angle between the endpoints is 45° from horizontal, so any movement to the left at the start would be misguided.
Similarly, leftward moves in the middle of the path do not help either — a path which zig-zags back and repeats some X-coordinates can be altered to take a more direct route with a lower total radiation dose.
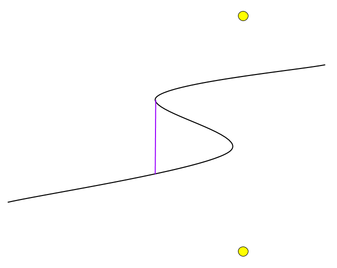
Solution #1: Hill-climbing
This optimization problem is well-suited for hill-climbing because it is easy to iteratively take a reasonable path and "nudge" it towards a better path in such a way that it will converge quickly towards a local minimum.
How many local minima are there? Since we should never move left, and there's only one or two islands, the optimal paths can only take so many forms. With one island, the optimal path will either go above the island, or go below it. With two islands, the optimal path will either go above both islands, between the two islands, or below both islands.
So if we start with a reasonable path for each of these forms and hill-climb from there, we will find each of the two or three local minima.
An easy way to do this is to model a path as a series of many small straight line segments. For each such segment, we can use calculus to find the amount of radiation received along that part of the path. Let's consider one such segment, running from (x1,y1) to (x2,y2), that we travel along between time 0 and time 1 (we've rescaled the times for convenience). Then the x and y coordinates, as a function of time t, are:
x(t) = x1 + t(x2-x1)
y(t) = y1 + t(y2-y1)
Suppose that there are two islands (the one island case is just a simpler version of this), and the y coordinates of the islands are yi1 and yi2. (Recall that the x coordinates of both islands are 0.) Then the total amount of radiation is the definite integral from 0 to 1 of:
[1 + 1 / (x(t)2 + (y(t)-yi1)2)) + 1 / (x(t)2 + (y(t)-yi2)2))] × [sqrt((x2-x1)2 + (y2-yi1)2))] dt
This integral can be solved exactly, but that's not necessary. Multiplying the length of the segment by the average of the dose rates at the endpoints of the segment is sufficiently accurate, if enough segments are used.
The question is how to find the right positions for our segments. We can lay down a rough path with endpoints whose X-coordinates are fixed and evenly-spaced between -10 and +10. Now, the Y-coordinates are a vector of real numbers, and we need to optimize that vector.
We can use gradient descent to do this — we need to iterate finding a direction to move the vector in such that the total radiation decreases.
Adjusting one value at a time doesn't work — even if a particular point needs to be moved upward, if we move only that one point upward, we'll soon be increasing the total radiation dose because the path will have a "kink" in it. But almost any other scheme will do — choosing an interval of points and nudging them all up or down in a triangular shape, moving the points in the middle more than the points at the end, will preserve the smoothness of the path. Other more sophisticated nonlinear optimization techniques like the BFGS algorithm work also.Solution #2: Calculus of Variations
We can consider the Y-coordinate of the ship to be a function of its X-coordinate and write the total radiation dose as an integral involving that function, then use techniques from the calculus of variations to minimize it. The Euler-Lagrange equation gives us a condition, expressed as a differential equation, that any solution must satisfy. This condition is entirely local, so if we knew the initial direction the ship should travel, we could find the entire path by using a numerical integration technique such as a Runge–Kutta method, to find a solution to the differential equation using the known initial conditions. However, we don't know the initial direction of the boat — we only know its starting and ending positions!
If we guess an initial direction for the boat that's reasonable, then integrating will trace out a path, but the y-coordinate of the endpoint will probably not be right. So, we can do a binary search to find the initial direction that does lead us to the desired endpoint. If we repeat the binary search for ranges that correspond to each of the forms the path can take, then we will find the optimal path.
Simple numerical integration techniques using finite differences are accurate enough to solve this problem, but one has to be careful of initial directions that point too directly towards an island or that have too large a slope, as those cases can have large numerical errors that might cause the binary search to take the wrong branch.
KalininN used this method to solve the Small dataset, and his solution would have worked for the Large with some minor tweaking.
Solution #3: Dynamic Programming
Another approach is to overlay a grid of points on the map, and use dynamic programming to find the optimal path through them. This is possible because the precision bound for this problem was not too strict, but it is still difficult to get right. A grid with too few points cannot model the optimal path accurately enough to get the right answer, and a grid with too many points would result in a dynamic programming problem that is too big to solve in time.
Gennady.Korotkevich, the only contestant to solve the Large dataset, successfully used this approach. He had two insights that made this method workable.
The ship's path is largely horizontal, with gradual changes in angle; the problem is mostly a question of how to carefully modulate the boat's vertical position. So the grid of points can have coarser horizontal granularity than vertical granularity; Gennady used a ratio of 20 to 1. In the final minutes of the contest, Gennady was testing two solutions, which only differed in their horizontal granularity. The coarser grid turned out to be more accurate, because it was able to model angles more precisely. A grid that was finer in both the horizontal and vertical directions would have been more accurate, but might have been too slow.
The second insight was that the path should have no segments which have a very steep
angle, so when computing the optimal value for a point in one column, only
points in the previous column within a certain vertical range need to be considered.
The size of that range was controlled by a constant called MAGIC in
Gennady's code. His solution ran in well
under the time limit allowed for the Large, and the answers were within our
somewhat generous error bounds.
It is possible to get a very accurate result quickly with this method by starting with a coarse grid, finding the optimal path in that grid, then iteratively improving the path by using finer and finer grids overlaying the space close to the path.
You can download our contestants' submissions to this problem (and others) from the Finals scoreboard.