Google Code Jam Archive — Round 2 2016 problems
Overview
Round 2 turned up the heat with some tougher problems. Even the easiest one, Rather Perplexing Showdown, can be tough depending on how you approach it. Red Tape Committee requires some standard dynamic programming techniques and a perhaps counterintuitive insight about probability. The Gardener of Seville is an unusual construction problem that is not trivial to implement even when you know what to do, and Freeform Factory is a tricky graph/matching problem.
The first hour of the contest saw many solves of A and B, and some correct answers to the tougher larges trickled in. SnapDragon was the first to crack C-large, at 44:09. austrin snagged the first D-large solution at 55:45, and had the only one until reigning champion Gennady.Korotkevich solved it at 1:11:07, jumping to the top of the scoreboard. For a while, many contestants were one problem away from 100, but EgorKulikov reached it first with a penalty time of 1:55:43. EgorKulikov had two wrong tries on one problem, so a tense 8 minutes passed in which another contestant could have jumped into first place, but this did not happen and victory was secured. Ahyangyi, eatmore, and betaveros followed up with our other three perfect scores.
Although the results are provisional until confirmation emails are sent, the top 500 required at least 46 points (often all of A and B plus one other Small) plus some speed, and the top 1000 required 29 points (at least one Large, usually A) plus some speed. Congratulations to the top 1000... wear your 2016 Code Jam T-shirt with pride! The top 500 will join us in Round 3 to compete for one of 25 tickets to the World Finals in New York in August! Even if you didn't advance or win a T-shirt in this round, remember that DCJ Round 1 offers another chance at a T-shirt and a trip to New York; it will take place on May 29.
Cast
Problem A (Rather Perplexing Showdown): Written by Ian Tullis. Prepared by Taman (Muhammed) Islam and Ian Tullis.
Problem B (Red Tape Committee): Written by Ian Tullis. Prepared by Karol Pokorski.
Problem C (The Gardener of Seville): Written and prepared by Petr Mitrichev and Ian Tullis.
Problem D (Freeform Factory): Written by Petr Mitrichev. Prepared by Pablo Heiber and Petr Mitrichev.
Solutions and other problem preparation and review by David Arthur, Shane Carr, John Dethridge, Minh Doan, Taman (Muhammed) Islam, Chieu Nguyen, Nathan Pinsker, Karol Pokorski, Yerzhan Utkelbayev, Jonathan Wills, and Josef Ziegler.Analysis authors:
- Rather Perplexing Showdown: Ian Tullis
- Red Tape Committee: David Arthur and Ian Tullis
- The Gardener of Seville: Timothy Loh
- Freeform Factory: Pablo Heiber, Petr Mitrichev and Amit Weinstein
A. Rather Perplexing Showdown
Problem
You've been asked to organize a Rock-Paper-Scissors tournament. The tournament will have a single-elimination format and will run for N rounds; 2N players will participate.
Initially, the players will be lined up from left to right in some order that you specify. In each round, the first and second players in the lineup (starting from the left) will play a match against each other, and the third and fourth players in the lineup (if they exist) will play a match against each other, and so on; all of these matches will occur simultaneously. The winners of these matches will remain in the lineup, in the same relative order, and the losers will leave the lineup and go home. Then a new round will begin. This will continue until only one player remains in the lineup; that player will be declared the winner.
In each Rock-Paper-Scissors match, each of the two players secretly chooses one of Rock, Paper, or Scissors, and then they compare their choices. Rock beats Scissors, Scissors beats Paper, and Paper beats Rock. If one player's choice beats the other players's choice, then that player wins and the match is over. However, if the players make the same choice, then it is a tie, and they must choose again and keep playing until there is a winner.
You know that the players this year are stubborn and not very strategic. Each one has a preferred move and will only play that move in every match, regardless of what the opponent does. Because of this, if two players with the same move go up against each other, they will keep tying and their match will go on forever! If this happens, the tournament will never end and you will be a laughingstock.
This year, there are R players who prefer Rock, P players
who prefer Paper, and S players who prefer Scissors. Knowing this,
you want to create a lineup that guarantees that the tournament will go to
completion and produce a single winner — that is, no match will ever be a
tie. Your boss has asked you to produce a list of all such lineups (written
in left to right order, with R, P, and S
standing for players who prefer Rock, Paper, and Scissors, respectively),
and then put that list in alphabetical order.
You know that the boss will lazily pick the first lineup on the list; what will
that be? Or do you have to tell your boss that it is IMPOSSIBLE to
prevent a tie?
Input
The first line of the input gives the number of test cases, T. T lines follow; each represents one test case. Each test case consists of four integers: N, R, P, and S, as described in the statement above.
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1) and y is
either IMPOSSIBLE or a string of length 2N
representing the alphabetically earliest starting lineup that solves the
problem. Every character in a lineup must be R, P, or
S, and there must be R Rs, P
Ps, and S Ss.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1 GB.
R + P + S = 2N.
0 ≤ R ≤ 2N.
0 ≤ P ≤ 2N.
0 ≤ S ≤ 2N.
Small dataset (Test Set 1 - Visible)
1 ≤ T ≤ 25.
1 ≤ N ≤ 3.
Large dataset (Test Set 2 - Hidden)
1 ≤ T ≤ 75.
1 ≤ N ≤ 12.
Sample
4 1 1 1 0 1 2 0 0 2 1 1 2 2 2 0 2
Case #1: PR Case #2: IMPOSSIBLE Case #3: PSRS Case #4: IMPOSSIBLE
In sample case #1, there are only two players and the tournament will
consist of one round. It doesn't matter what order the two line up in; the
Paper-using player will defeat the Rock-using player. You will give
your boss the alphabetically ordered list PR, RP, and
the first element is PR.
In sample case #2, the only two players both play Rock, so a tie is
unavoidable.
In sample case #3, there are four players and the tournament will go on for two
rounds. In the first round, the first player (Paper) will lose to the second
player (Scissors), and the third player (Rock) will defeat the fourth player
(Scissors). The second round lineup will be PR, and the first
remaining player (Paper) will defeat the other remaining player (Rock), so the
tournament will end with a winner and no ties.
Here is an illustration of the tournament for sample case #3:
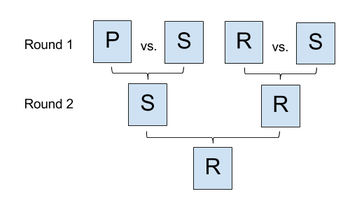
PSSR will appear on the list you give to
your boss, but PSRS is alphabetically first.
In sample case #4, the only way to organize the first round such that there are no ties is to create two matches with one Rock player and one Scissors player. But both of those matches will have a Rock winner, and when these two winners go on to face each other, there will be a tie.
B. Red Tape Committee
Problem
You are the head of the Department of Redundancy Reduction and Superfluity Shrinkage. Currently, the department cannot agree on whether there is too much "red tape" (inefficiency) in the department itself. They have asked you to form a Red Tape Committee to vote on the issue.
The department has N members. For each member, you know the probability Pi that that member will vote "Yes". If a member does not vote "Yes", they necessarily vote "No"; nobody abstains.
You must choose exactly K members to be on the committee. The department rules dictate that K must be an even number to allow for ties, which are seen as part of a healthy bureaucracy.
If you choose committee members to maximize the probability of a tie, what is that probability?
Input
The first line of the input gives the number of test cases, T. T test cases follow; each consists of two lines. The first line of a test case consists of two integers N and K, the sizes of the department and the committee. The second line of a test case consists of N decimal values Pi; each has exactly two decimal places of precision and represents the probability that the i-th department member will vote "Yes".
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1) and y is
a floating-point number: the maximum possible probability of a tie.
y will be considered correct if it is within an absolute or
relative error of 10-6 of the correct answer. See the
FAQ for an
explanation of what that means, and what formats of real numbers we accept.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 100.
2 ≤ K ≤ N.
K is even.
0.00 ≤ each Pi ≤ 1.00.
Small dataset (Test Set 1 - Visible)
Time limit: 60 seconds.
2 ≤ N ≤ 16.
Large dataset (Test Set 2 - Hidden)
Time limit: 120 seconds.
2 ≤ N ≤ 200.
Sample
3 2 2 0.50 0.50 4 2 0.00 0.00 1.00 1.00 3 2 0.75 1.00 0.50
Case #1: 0.5 Case #2: 1.0 Case #3: 0.5
In sample case #1, you must use the only two available department members to form the committee. That committee will tie only if the two committee members vote differently, which will happen half the time. (Without loss of generality, choose the vote of the first. Then the probability that the second will vote the other way is 0.5.)
In sample case #2, the best strategy is to pick one of the members with "Yes" probability 0.00 and one of the members with "Yes" probability 1.00. This guarantees a tie.
In sample case #3, suppose that we pick the two members with "Yes" probabilities of 0.50 and 0.75. A tie will happen if the first one votes "Yes" and the second one votes "No" (probability 0.5 * 0.25 = 0.125), or if the first one votes "No" and the second one votes "Yes" (probability 0.5 * 0.75 = 0.375). So the total probability of a tie is 0.125 + 0.375 = 0.5. Choosing the two members with "Yes" probabilities of 0.50 and 1.00 would also make the tie probability 0.5, since the 1.00 member will vote "Yes" and the 0.50 member must vote "No". Choosing the two members with "Yes" probabilities of 0.75 and 1.00 would make the tie probability only 0.25, since the 1.00 member will vote "Yes" and the 0.75 member must vote "No". So 0.5 is the best we can do.
C. The Gardener of Seville
Problem
You are the Gardener of Seville, a minor character in an opera. The setting for
the opera is a courtyard which is a rectangle of unit cells, with R rows
and C columns. You have been asked to install a maze of hedges in the
courtyard: every cell must contain a hedge that runs diagonally from one corner
to another. For any cell, there are two possible kinds of hedge: lower left to
upper right, which we represent with /, and upper left to lower
right, which we represent with \. Wherever two hedges touch, they
form a continuous wall.
Around the courtyard is an outer ring of unit cells, one cell wide, with the four corners missing. Each of these outer cells is the home of a courtier. The courtiers in these outer cells are numbered clockwise, starting with 1 for the leftmost of the cells in the top row, and ending with 2 * (R + C) for the topmost cell in the left column. For example, for R = 2, C = 2, the numbering in the outer ring looks like this. (Note that no hedges have been added yet.)
12
8 3
7 4
65
In this unusual opera, love is mutual and exclusive: each courtier loves exactly one other courtier, who reciprocally loves only them. Each courtier wants to be able to sneak through the hedge maze to his or her lover without encountering any other courtiers. That is, any two courtiers in love with each other must be connected by a path through the maze that is separated from every other path by hedge walls. It is fine if there are parts of the maze that are not part of any courtier's path, as long as all of the pairs of lovers are connected.
Given a list of who loves who, can you construct the hedge maze so that every
pair of lovers is connected, or determine that this is IMPOSSIBLE?
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each consists of one line with two integers R and C, followed by another line with a permutation of all of the integers from 1 to 2 * (R + C), inclusive. Each integer is the number of a courtier; the first and second courtiers in the list are in love and must be connected, the third and fourth courtiers in the list are in love and must be connected, and so on.
Output
For each test case, output one line containing only
Case #x:, where x is the test case number (starting
from 1). Then, if it is impossible to satisfy the conditions, output one more
line with the text IMPOSSIBLE. Otherwise, output R more
lines of C characters each, representing a hedge maze that satisfies the
conditions, where every character is / or \. You may
not leave any cells in the maze blank. If multiple mazes are possible, you may
output any one of them.
Limits
Time limit: 40 seconds per test set.
Memory limit: 1 GB.
Small dataset (Test Set 1 - Visible)
1 ≤ T ≤ 100.
1 ≤ R * C ≤ 16.
Large dataset (Test Set 2 - Hidden)
1 ≤ T ≤ 500.
1 ≤ R * C ≤ 100.
Sample
4 1 1 1 4 3 2 1 3 1 8 2 7 3 4 5 6 2 2 8 1 4 5 2 3 7 6 1 1 1 3 2 4
Case #1: / Case #2: //\ Case #3: // \/ Case #4: IMPOSSIBLE
In Case #3, the following pairs of courtiers are lovers: (8, 1), (4, 5), (2, 3), (7, 6). Here is an illustration of our sample output:
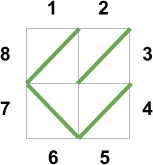
For Case #3, note that this would also be a valid maze:
/\
\/
In Case #4, the courtyard consists of only one cell, so the courtiers living
around it, starting from the top and reading clockwise, are 1, 2, 3, and 4.
There are only two possible options to put in the one cell: / or
\. The first of these choices would form paths from 1 to 4, and
from 2 to 3. The second of these choices would form paths from 1 to 2, and from
3 to 4. However, neither of these helps our lovesick courtiers, since in this
case, 1 loves 3 and 2 loves 4. So this case is IMPOSSIBLE, and
the opera will be full of unhappy arias!
D. Freeform Factory
Problem
You have just built a brand new factory. Your factory has N different machines, and each machine needs to be operated by exactly one worker for the factory to function well.
You have also hired N workers to operate those machines. Since you were in a hurry when you hired them, you did not check whether they actually know how to operate your machines. Now you have finally asked them, and so you have the information on whether the i-th worker can operate the j-th machine, for each i and j.
In a typical working day, the workers will arrive at the factory in a random order, which can be different each day. As each worker arrives, they will find all machines that they know how to operate and that do not already have an operator. They will choose one of those at random and operate it for the whole working day. If all machines they know how to operate already have an operator, they will not work that day. Your goal is to make sure that all machines are being operated each working day, regardless of what order the workers arrive in and which machines they choose.
For example, suppose there are two workers A and B, and two machines 1 and 2. Suppose that A knows how to operate 1 and 2, and B knows how to operate 1 but not 2. If worker B arrives first, he will pick machine 1, then when worker A arrives she will have to choose 2, and the factory will work well. However, if worker A arrives first, it might happen that she chooses to operate 1 on that day, and then when worker B arrives he does not have anything to do, leaving machine 2 without an operator, and causing your factory to waste a whole day!
As another example, suppose there are two workers A and B, and two machines 1 and 2, and that A knows how to operate 1 but not 2, and B does not know how to operate anything. Then, regardless of the order in which the workers arrive, the factory will not be able to function well.
Before you open your factory, in order to guarantee that the factory will constantly function well, you can teach your workers how to operate machines. It costs one dollar to give a single worker a lesson on how to operate a single machine. Each lesson involves only one worker and only one machine, but you can teach any number of lessons to any number of workers, and the same worker can receive multiple lessons. You cannot make a worker forget how to operate a machine if they already know how to operate it.
For example, both examples above can be fixed by teaching worker B to operate machine 2. In that case each machine is guaranteed to have an operator every day, regardless of which order the workers arrive in and which machines they choose to operate when they have more than one possibility.
What is the minimum amount of dollars you need to spend on training workers to make sure the factory functions well every day?
Input
The first line of the input gives the number of test cases, T. T
test cases follow. Each test case starts with one line with an integer
N, the number of workers (and machines). This line is followed by N lines with
a string of N characters each. The j-th character on the i-th of those lines is
1 if the i-th worker knows how to operate the j-th machine, and
0 otherwise.
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1), and y is
a non-negative integer: the minimum amount of dollars you need to spend to make sure that
all N machines will always have an operator.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1 GB.
1 ≤ T ≤ 100.
Small dataset (Test Set 1 - Visible)
1 ≤ N ≤ 4.
Large dataset (Test Set 2 - Hidden)
1 ≤ N ≤ 25.
Sample
5 2 11 10 2 10 00 3 000 000 000 1 1 3 000 110 000
Case #1: 1 Case #2: 1 Case #3: 3 Case #4: 0 Case #5: 3
Sample cases #1 and #2 are the ones described in the problem statement.
In sample case #3, nobody knows how to do anything! One optimal strategy is to teach worker A to operate machine 1, worker B to operate machine 2, and worker C to operate machine 3.
In sample case #4, no action is necessary. There is only one worker, and the worker already knows how to operate the one machine.
In sample case #5, worker B already knows how to operate machines 1 and 2. One optimal strategy is to teach worker A to operate machine 3, and make A the only worker who can operate that machine. But now we have to consider that B might operate either machine 1 or 2 upon arrival, so C needs to be able to operate the one not chosen by B. So C must be taught to operate both 1 and 2.
Analysis — A. Rather Perplexing Showdown
Rather Perplexing Showdown: Analysis
There are multiple ways to attack this problem. We will present two methods for building the correct tournament tree, and a method for finding the arrangement of that tree that produces the alphabetically earliest lineup. It is possible to combine the tree building and tree optimization methods into a single algorithm, but we present the analysis this way for ease of explanation.
Building the tree: starting from the beginning
Let's start from the beginning of the tournament and create each new round. At
any point, you have some number of Rs, Ps, and
Ss remaining, and you can only create RP,
RS, and PS matches, because anything else would
result in a tie. Call the number of RP matches you will create
x — that is, you will make x of the Rs match
up with x of the Ps. Then all other Rs
must face Ss, so you will create R-x RS
matches. There will be P-x leftover Ps and
S-(R-x) leftover Ss, and these numbers must be
equal to avoid creating tied matches, so P-x =
S-R+x and x = (R+P-S)/2. If
this x causes an impossible situation (e.g, there must be more
RP matches than there are Rs or Ps),
then the answer is IMPOSSIBLE. Otherwise, match the players
accordingly, note the winners (all RPs become Ps, all
RSs become Rs, and all PSs become
Ss), and then you have a smaller instance of the same problem.
This strategy tells you whether the tournament will end, and how to make all
your matchups; with that information and some careful bookkeeping along the
way, you can generate the entire tree.
Building the tree: starting from the end
Let's start from the end of a tournament instead. Suppose that the winning
player is a P. What do we know about the match that produced
that winner? One of the participants must have been that P, and
the other must have been the opponent that the P defeated, namely,
an R. That R must have defeated an S,
and so on. That is, for any node in the tournament tree, including the bottom
(winning) node, we can easily regenerate the entire part of the tree that led
to it!
This also implies that for a given N, there is only one possible
(R, P, S) triplet that will produce a
successful tournament ending in R, and likewise for P
and S. Almost all triplets are doomed to fail! There are only
three valid ones for any N, and each of them must produce a different
winner.
So, we can try all three possible winners (R, P, and
S) for every value of N from 1 to 12, and store the
resulting tournament trees and their numbers of Rs,
Ps, and Ss. Then, for each test case, either the
given N, R, P, and S values match one of the stored
trees, or we know the case is IMPOSSIBLE.
Finding the alphabetically earliest lineup
Having the tournament tree is not enough, because a tree can generate many
possible lineups. For any internal (non-leaf) node in the tree, you can swap
the two branches; this does not change the tree, but it does change the initial
lineup! For instance, the lineups PSRS, PSSR,
RSPS, RSSP, SPRS, SPSR,
SRPS, and SRSP all represent the same tree. There are
2N-1 internal nodes in the tree, and we can't try all 2 to
the (2N-1) ways of flipping or not flipping each of them.
Fortunately, we don't have to.
Consider any pair of players who face off in the first round; let's say they're using moves X and Y, where X is alphabetically earlier than Y. These two players will contribute to two consecutive characters in the lineup; either XY or YX, depending on whether we flip their node. Flipping other nodes in the tree may move this pair of characters around in the final lineup, but it cannot reverse or separate them. So we have nothing to lose by choosing XY; this decision is totally independent of whatever we do with other nodes later. More generally, for any node, we should put the "alphabetically earlier" branch before the "alphabetically later" branch. Moreover, we should optimize shallower nodes in the tree before optimizing deeper nodes, so that we can be sure that we're only making decisions about branches that are already themselves alphabetically optimized.
So we can start with any lineup corresponding to our tree (ideally, whatever came out of our algorithm earlier), and first examine the lineup in 2N-1 chunks of length 2 and swap the letters in each chunk whenever that would make the chunk alphabetically earlier. Then we can examine the lineup in 2N-2 chunks of length 4, and swap the subchunks of length 2 in each chunk whever that would make the chunk alphabetically earlier. And so on, until we've examined and possibly swapped the 2 chunks of length 2N-1; that final lineup will be our alphabetically earliest answer.
Analysis — B. Red Tape Committee
Red Tape Committee: Analysis
This problem poses two challenges: figuring out which sets of members to consider as possible committees, and calculating the tie probability for each committee. In the Small dataset, brute force will suffice for both of these subproblems. However, in the Large dataset, we will need more efficient methods for both of them.
Who should we choose?
One might think that in order to create ties, we should choose from among the most "moderate" department members — that is, the ones with Yes probabilities closest to 0.5. In fact, the opposite is true! The best way to create a tie is to choose department members from one or both extremes. That is, we should choose the M (possibly zero) of the department members with the lowest Yes probabilities, and the K - M of the department members with the highest Yes probabilities. This makes sense intuitively; to take an extreme case, a committee of two members with Yes probabilities of 0.00 and 1.00 will always tie, whereas a committee of two members with Yes probabilities of 0.50 and 0.50 will tie only half the time. Experimentation bears this idea out. But how can we prove it?
Without loss of generality, let's sort the members in increasing order of Yes probability. Suppose that we have chosen a committee of these members that maximizes the tie probability. If there are multiple such committees, suppose that we have chosen the one that also minimizes the sum of the members' indexes in that sorted list.
We'll show that this set consists of the M (possibly zero) leftmost members and the K - M rightmost members, as described above. Suppose that there exist the following: a member X, who is in our set, and members Y and Z, who are not in our set, and that they are in the left to right order Y, X, Z. Fix all the other members and consider the tie probability as a function of member X's Yes probability. This is a linear function. If it has slope 0, then we can get an equally good set with a smaller sum of member indices by replacing X with Y. If it has slope > 0, we can get a better set by replacing X with Z. If it has slope < 0, we can get a better set by replacing X with Y. So X must not exist!
Therefore, we can try all values of M and consider only those committees. This linear search adds a multiplier of O(K) to the running time of the calculation of tie probabilities. The one-time sort also adds a single O(N log N) term.
How likely is a tie?
For a large committee, we cannot explicitly consider all 2N possible voting outcomes. Many of these outcomes are very similar, and we would do a lot of redundant work. This is an ideal situation for dynamic programming.
Let's build a table in which the columns represent the committee members, the rows represent the total number of Yes votes so far, and the numbers in the cells measure the probability of being in the situation represented by that row and column. We start with a 1.00 in the upper left cell, which represents the situation before anyone has voted; there is a 100% chance that there will be no "Yes" votes at this stage. Let's consider a committee with Yes probabilities of 0.10, 0.20, 0.50, and 1.00. We will label the columns in that order (although the order does not matter).
- init 0.10 0.20 0.50 1.00
0 1.00 ---- ---- ---- ----
1 ---- ---- ---- ---- ----
2 ---- ---- ---- ---- ----
3 ---- ---- ---- ---- ----
4 ---- ---- ---- ---- ----
When the first member votes, either the vote will be "Yes" with 10% probability (and we will have one Yes vote), or "No" with 90% probability (and we will have zero Yes votes). So the 1.00 value gets split up among two cells in the next column: the "0 Yes votes after 1 member has voted" and "1 Yes vote after 1 member has voted" cells.
- init 0.10 0.20 0.50 1.00
0 1.00 0.90 ---- ---- ----
1 ---- 0.10 ---- ---- ----
2 ---- ---- ---- ---- ----
3 ---- ---- ---- ---- ----
4 ---- ---- ---- ---- ----
Let's look at the "0 Yes votes after 1 member has voted" cell, which represents 90% of all possible situations after the first member has voted. That probability will feed into two of the cells in the next column: the one just to the right, and the one just below that. Since the second member has an 80% probability of voting No, 80% of that 90% possibility space branches off to the "0 Yes votes after 2 members have voted" cell. The other 20% of that 90% branches off to the "1 Yes vote after 2 members have voted" cell.
- init 0.10 0.20 0.50 1.00
0 1.00 0.90 0.72 ---- ----
1 ---- 0.10 0.18 ---- ----
2 ---- ---- ---- ---- ----
3 ---- ---- ---- ---- ----
4 ---- ---- ---- ---- ----
And now for the "1 Yes vote after 1 member has voted" cell, which represents 10% of all possible situations after the first member has voted. Again, that probability will feed into the right and down-and-right neighboring cells in the next column. Note that we add 0.08 to the existing value of 0.18 in the "1 Yes vote after 2 members have voted" cell; there are multiple ways of getting to that cell. The power of dynamic programming is that it merges separate possibilities like this and lets us consider them together going forward; this prevents an exponential increase in the number of possibilities.
- init 0.10 0.20 0.50 1.00
0 1.00 0.90 0.72 ---- ----
1 ---- 0.10 0.26 ---- ----
2 ---- ---- 0.02 ---- ----
3 ---- ---- ---- ---- ----
4 ---- ---- ---- ---- ----
Continuing in this way, we can fill in the whole table. Note that every column sums to 1, as expected.
- init 0.10 0.20 0.50 1.00
0 1.00 0.90 0.72 0.36 0.00
1 ---- 0.10 0.26 0.49 0.36
2 ---- ---- 0.02 0.14 0.49
3 ---- ---- ---- 0.01 0.14
4 ---- ---- ---- ---- 0.01
The tie probability is the value in the "2 Yes votes after 4 members have voted" cell: 0.49. We could have optimized this further by not considering any rows below the number of Yes votes needed for a tie. In practice, in problems like this, one should store the logarithms of probabilities instead of the actual values, which can become small enough for floating-point precision errors to matter.
The number of calculations in this method is proportional to the dimensions of the table, each of which is proportional to K, so the running time of this part is O(K2). Combining that with the O(K) method of selecting committees, the overall running time of our approach is O(K3) + O(N log N). Since K cannot exceed N, and N cannot exceed 200 for the Large, this is fast enough, albeit not optimal. (For example, we could do a ternary search on the value of M mentioned above, instead of a linear search.)
Analysis — C. The Gardener of Seville
The Gardener of Seville: Analysis
Small dataset
Small dataset
For the Small dataset, there are at most 16 cells in the courtyard that we must assign hedge directions to, a total of at most 65536 different hedge mazes. Note that because every cell must have a diagonal hedge, any maze creates a bijection between courtiers; it is impossible for the paths used by two different pairs of lovers to intersect, so we don't need to worry about that. We can use brute force to generate and check all possible hedge mazes, as long as we can efficiently work out which outer cells are paired up through the hedge maze. This can be done in various ways, including:
- Consider hedges to be mirrors, and imagine shining a beam of light into the maze from an outer cell, perpendicular to the edge it's on. At each cell the light will reflect off the cell's mirror at a 90 degree angle and continue to the next cell in its new direction. It repeatedly bounces off mirrors until it exits the maze at the cell it's paired with.
- Imagine drawing both hedges in each cell, splitting each cell into four quadrants. We can represent the maze as a graph in which the nodes are these quadrants, and there are edges between adjacent quadrants that are not blocked by part of a hedge. We can find which courtiers are paired by starting at the node corresponding to that courtier's starting edge of the maze, and traversing the graph until we reach another edge. Equivalently, we can find the connected components of the graph.
Large dataset
The Large dataset has test cases with up to 100 cells, which is too large for our
brute force approach. A more fruitful approach is to take the given pairs
and install hedges so that those pairs are connected. The easiest cases would be
connecting two cells which are adjacent (either along an edge or around a
corner). For example, to connect the two outer cells adjacent to the upper left
corner, a single / hedge is sufficient. Does it ever make sense to
connect them any other way? The illustration for test case 3 from the sample input
connects the two outer cells adjacent to the upper right corner via a longer
winding path, but it would also work to make this connection direct and leave the
center of the garden unreachable. The direct
connection covers just two triangular quadrants (as defined in the Small dataset
section) in the corner, and it is easy to see that any other possible path
between the two cells also covers these two quadrants. Thus there is no reason
not to use this direct path if we need to connect the cells at a corner.
How about outer cells next to each other along an edge? These can be easily connected using two hedges, which covers four triangular quadrants. All possible connections will necessarily cover the two quadrants at the edge of the board, but we can construct paths which do not cover the other two quadrants. However, any path that does not use those two quadrants is guaranteed to block them off and make them inaccessible from other edges. Thus, any path between the two cells will either cover the four quadrants forming the simplest path, or render some of them unusable; there is no reason to use anything more complex than the simplest path.
If every pair to connect has a similarly optimal path which we can easily determine, then we can solve the problem by installing hedges so each pair is connected via its respective optimal path, and if any of the paths intersect then there is no solution. Consider, however, a pair between outer cells on the left and right sides of the garden. Depending on the other connections we need to make, we may be able to freely choose between (for example) having the path go through the top half of the garden and the bottom half of the garden. As such, there isn't a clear single optimal path for connecting this pair. However, we can consider uppermost and lowermost paths, which leave the most space for paths below and above them, respectively. For an uppermost path, for example, we want to take the least space possible to connect the pair, and all the pairs above it. turns out there is a optimal way to connect such pairs.
For the rest of the analysis, we will assume that there is a solution to the problem. If there is a solution, then our strategy will provide a way to find it. If there is no solution, our strategy may not be correct but we can easily detect that it fails by checking the hedge maze as we did in the Small solution.
Define a 'group of pairs' as a non-zero number of pairs where all the outer cells used form a fully contiguous section around the perimeter (but not the full perimeter). For a pair connecting the left and right sides of the garden, we can consider the group of pairs above the path connecting this pair, and the group of pairs above and including this pair. Every group of pairs has an optimal set of triangular quadrants to join all pairs in that section. Similar to before, optimality here means that we can install hedges to connect each pair in the group without covering quadrants outside the optimal set (this property is sufficiency), and if all pairs in the group are connected, no paths from other pairs can ever cover quadrants inside the set (this property is necessity).
We already know the optimal sets for the groups with a single pair of adjacent outer cells. If we have two groups of pairs, which together would form a larger group of pairs, the optimal set will be the union of the optimal sets for the two smaller groups. We can prove that this meets both the sufficiency and necessity properties (as stated before, this requires the assumption that there is a solution).
Consider again the case of a pair connecting the left and right sides of the garden. If we have the optimal set for the group of pairs above this pair, then we can try and extend this to the optimal set for the group of pairs above and including this pair. It makes sense to try and make the path for this pair as high up as possible, staying as close as possible to the paths above it. It can be proven that including this path makes a new optimal set. In general, this works for any non-adjacent pair. If we have the optimal set of quadrants for the group of pairs on one side of a pair, we can extend it by adding a path that stays as close to those quadrants as possible. This means we can inductively find optimal sets of quadrants until we cover all the pairs (note that we did not define all pairs as a valid group of pairs, as the definition of optimality doesn't work for that case).
These ideas give us the following algorithm:
- Start with no hedges in the garden
- Iterate over pairs, in increasing order of distance (along the perimeter)
between the two cells. Ties can be broken arbitrarily.
- Let the two outer cells be A and B, such that A→B clockwise around the edge is shorter than counterclockwise. Due to the chosen iteration order, we've already built paths for all points on the left side of the A→B path we're going to construct.
- Walk through maze starting at A (the mirror analogy is useful here). We want to stay to the left as much as possible, so if we get to a cell without a hedge installed we pick one so that we turn left. Once we exit the maze, check if we actually made it to B. (If there is no solution we might end up somewhere else.)
- Fill in remaining cells arbitrarily
A sample implementation of this in Python is provided below. We encode directions with integers, which allows us to rotate direction and calculation movement easily using bitwise operations and array lookups.
def position(v, R, C):
# Map from outer cell number to a direction facing into the maze
# and the position of the outer cell
# 0->downwards, 1->leftwards, 2->upwards, 3->rightwards
if v <= C: return 0, v-1, -1
v -= C
if v <= R: return 1, C, v-1
v -= R
if v <= C: return 2, C-v, R
v -= C
return 3, -1, R-v
def move(x, y, direction):
return x + [0,-1,0,1][direction], y + [1,0,-1,0][direction]
def solve(R, C, permutation):
board = [[None] * C for _ in range(R)]
size = 2*(R+C)
permutation = zip(permutation[::2], permutation[1::2])
permutation.sort(key=lambda(a,b): min((b-a)%size, (a-b)%size))
for start, end in permutation:
if (start-end) % size > R+C:
start, end = end, start
direction, x, y = position(start, R, C)
x, y = move(x, y, direction)
while 0<=x<C and 0<=y<R:
if board[y][x] is None:
board[y][x] = "/\\"[direction & 1]
direction ^= {"/": 1, "\\": 3}[board[y][x]]
x, y = move(x, y, direction)
if (x, y) != position(end, R, C)[1:]:
return "IMPOSSIBLE"
return "\n".join("".join(c or "/" for c in row) for row in board)
if __name__ == "__main__":
for t in range(1, input() + 1):
R, C = map(int, raw_input().split())
permutation = map(int, raw_input().split())
print "Case #%d:" % t
print solve(R, C, permutation)Analysis — D. Freeform Factory
As the first step in solving this problem, we will move it from worker/factory terms to graph terms: we are given a bipartite graph with N vertices in each part, and need to add the smallest amount of edges to this graph to guarantee that every maximal matching (one where it is impossible to add more edges) is a perfect matching (one which covers all vertices).
In order to determine that, we need to understand which bipartite graphs have the property that every maximal matching is perfect. One can tackle this part by drawing a few graphs on paper and trying to add edges one by one to find a maximal matching.
After a few experiments, we can form a hypothesis: every maximal matching is perfect if and
only if each connected component of the bipartite graph is a
complete bipartite graph
with same number of
vertices in each part. The "if" part is somewhat clear, but the "only if" part
looks surprising at first and definitely needs a formal proof, which you can find at the end of
this editorial. Here's an example of such graph:
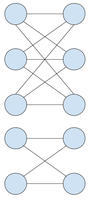
Now we can return to solving our problem. As the first step, we need to find the number of vertices in each half for each connected components of the graph. Let us put those numbers into a list of pairs, one pair per connected component: (p1, q1), (p2, q2), ... The above hypothesis tells us that we need to split this list into groups such that in each group the sum r of all ps equals the sum of all qs, those groups corresponding to the connected components of the graph after adding more edges. The number of added edges is the total number of edges in the resulting graph minus the number edges we have initially, and the number of edges in the resulting graph is equal to the sum of squares of rs. Thus we need to minimize the sum of squares of rs.
Since N is quite small — up to 25 — there are quite a few approaches that work, almost all revolving around dynamic programming/memoization.
Here is one possibility: for each subset Y of the (multi-)set X of pairs we have, and each number t between 0 and N, we will check if it is possible to group all components in Y into groups in such a way that there are several balanced groups with total size t, and possibly one unbalanced group with all remaining components. In case it is possible, we will find the smallest possible sum of squares of sizes of the balanced groups, denoted as dpY,t. Looking at dpX,N will give us the answer to the problem.
At first sight, it seems that we are considering 250 subsets here as we might have up to 50 components in the original graph (if we have no edges at all), but we can note that equal components are interchangeable, so a graph with no edges simply has 25 components of one type and 25 components of the other type, and thus has the total of 26*26=676 different subsets of components. The maximum amount of different subsets of components for N=25 is 43008, formed by the following initial components: 6×(0,1), 5×(1,0), 3×(1,1), 1×(1,2), 1×(1,3), 1×(1,4), 1×(2,1), 1×(2,2), 1×(3,1), 1×(3,2), 1×(4,1).
The most straightforward way to compute the dpY,t values is to use the so-called forward dynamic programming: after finding dpY,t, we will iterate over all ways to add a new element to the unbalanced group in Y, updating t in case the unbalanced group becomes balanced.
All that is left is to prove the hypothesis. We will prove by contradiction: assume that the hypothesis is false — in other words, that there exists a bipartite graph where every maximal matching is perfect, but one of its connected components is not a complete bipartite graph with same number of vertices in each part.
Consider such counterexample G with the smallest number of vertices (note that looking at the smallest counterexample is essentially the same as proving by induction). First of all, G is connected — otherwise any of its connected components would form a smaller counterexample. It is also clear that both its parts have the same number of vertices, as otherwise no perfect matching exists at all, while at least one maximal matching always exists, so we would have a contradiction. Since G is a counterexample, it is missing at least one edge. Let us say that the missing edge connects vertices a and b.
Consider any edge (a, c) that exists from a (there is one since G is connected). Consider the graph G' obtained by removing a, c and all their incident edges from G. Every maximal matching in this smaller graph is perfect, since it can be extended to a maximal matching in G by adding (a, c). And since G' has fewer vertices than G, it is not a counterexample to our hypothesis, and thus each connected component of G' is a complete bipartite graph with same number of vertices in each part.
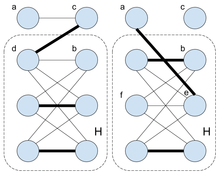
Let us look at the connected component H of G' containing b. There are three cases, each leading to a contradiction:
- There is at least one edge (d, c) in G from H to c. Since all connected components of G' are complete, we can easily build a matching M' in G' that covers all vertices except d and b. By adding the edge (d, c) to this matching we get a matching M in G. Matching M is maximal: its only two uncovered vertices are a and b, and there is no edge between them. M is not perfect, and thus we get a contradiction with the definition of G.
- There is no edge from H to c, but there exists an edge (a, e) from a to H. Consider any vertex f from H in a different part from e. Since H and all other connected components of G' are complete, we can now build a matching M' in G' that covers all vertices except e and f. By adding the edge (a, e) to this matching we get a matching M in G. Matching M is maximal: its only two uncovered vertices are f and c, and there is no edge between them since there is no edge between the entire H and c. M is not perfect, and thus we get a contradiction with the definition of G.
- Finally, if H is not connected to a and c, then G is disconnected, which is also a contradiction.
The first two contradiction cases are depicted below:
There is also a more beautiful argument leading to a contradiction which does not even require the counterexample G to be the smallest, but it can be a bit harder to come up with. Since G is connected, there is a simple path P between a and b. Since the graph is bipartite, P has odd length and covers some subset of the vertices, the same number from each part. We construct a maximal (therefore perfect) matching as follows: we take every odd edge along the path P, and then complete it with arbitrary edges. Now, we can change our choice of edges and take the even edges of P instead of the odd ones. As a result, our matching has one less edge, and vertices a and b are the only non-covered ones. Since a and b are not connected by an edge, we are left with a maximal matching which is not perfect, in other words a contradiction.