Google Code Jam Archive — Round 1C 2016 problems
Overview
In another Code Jam first, all three of the problems in this round allowed multiple answers per test case. Senate Evacuation was the easiest of the trio; many greedy approaches were possible. The other two were tougher, and even the Smalls required some insights on top of pure brute force. Slides! gave you nearly free rein to construct a graph with certain properties, and Fashion Police was set in New York, in a nod to our upcoming World Finals venue.
Contestant artberryx grabbed the first place slot with six correct submissions in 38 minutes and 49 seconds, and there were 144 perfect scores. To advance, you needed at least 52 points and some speed. Contestants who didn't solve the Slides! large quickly enough had to contend with Fashion Police, a problem in which the tempting greedy solution doesn't work.
We'll see our 3000 advancers — 1000 each from Rounds 1A, 1B, and 1C — in Round 2 and Distributed Round 1 on May 28 and 29. If you didn't advance in Round 1, thanks for participating, and we hope to see you again in the 2017 contest!
Cast
Problem A (Senate Evacuation): Written by Pablo Heiber. Prepared by Pablo Heiber and Yerzhan Utkelbayev.
Problem B (Slides!): Written by Pablo Heiber. Prepared by Pablo Heiber and Ian Tullis.
Problem C (Fashion Police): Written by Ian Tullis. Prepared by Jackson Gatenby and Ian Tullis.
Solutions and other problem preparation and review by Shane Carr, Taman (Muhammed) Islam, Yiming Li, Igor Naverniouk, Patrick Nguyen, Nathan Pinsker, Karol Pokorski, Steve Thomas, and Yerzhan Utkelbayev.
Analysis authors:
- Senate Evacuation: Ian Tullis
- Slides!: Nathan Pinsker
- Fashion Police: Pablo Heiber, Steve Thomas, and Ian Tullis
A. Senate Evacuation
Problem
A small fire started in the senate room, and it needs to be evacuated!
There are some senators in the senate room, each of whom belongs to of one of N political parties. Those parties are named after the first N (uppercase) letters of the English alphabet.
The emergency door is wide enough for up to two senators, so in each step of the evacuation, you may choose to remove either one or two senators from the room.
The senate rules indicate the senators in the room may vote on any bill at any time, even in the middle of an evacuation! So, the senators must be evacuated in a way that ensures that no party ever has an absolute majority. That is, it can never be the case after any evacuation step that more than half of the senators in the senate room belong to the same party.
Can you construct an evacuation plan? The senate is counting on you!
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case consists of two lines. The first line contains a single integer N, the number of parties. The second line contains N integers, P1, P2, ..., PN, where Pi represents the number of senators of the party named after the i-th letter of the alphabet.
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1) and y is
the evacuation plan. The plan must be a space-separated list of instructions,
in the order in which they are to be carried out, where each instruction is
either one or two characters, representing the parties of the senators to
evacuate in each step.
It is guaranteed that at least one valid evacuation plan will exist. If multiple evacuation plans are valid, you may output any of them.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 50.
No party will have an absolute majority before the start of the evacuation.
1 ≤ Pi ≤ 1000, for all i.
Small dataset (Test set 1 - Visible)
2 ≤ N ≤ 3.
sum of all Pi ≤ 9.
Large dataset (Test set 2 - Hidden)
2 ≤ N ≤ 26.
sum of all Pi ≤ 1000.
Sample
4 2 2 2 3 3 2 2 3 1 1 2 3 2 3 1
Case #1: AB BA Case #2: AA BC C BA Case #3: C C AB Case #4: BA BB CA
The sample output displays one set of answers to the sample cases. Other answers may be possible.
In Case #1, there are two senators from each of the parties A and B. If we remove one from each party every time, the perfect balance is maintained until evacuation is complete.
Case #2 proceeds as follows:
Initially in the room: 3 A, 2 B, 2 C.
Evacuate AA. Still in the room: 1 A, 2 B, 2 C.
Evacuate BC. Still in the room: 1 A, 1 B, 1 C.
Evacuate C. Still in the room: 1 A, 1 B.
Evacuate AB. Evacuation complete!
Note that it would not be valid to begin the evacuation with BC, which would leave 3 A, 1 B, and 1 C in the room; party A would have an absolute majority (3 out of 5 = 60%).
For Case #3, note that CC AB would also be a valid answer, and
C C AB is also valid even though it requires three evacuation
steps instead of two.
B. Slides!
Problem
Gooli is a huge company that owns B buildings in a hilly area. The buildings are numbered from 1 to B.
The CEO wants to build a set of slides between buildings that she can use to travel from her office in building 1 to her favorite cafe in building B. Slides, of course, are one-way only, but the buildings are tall and have elevators, so a slide can start in any building and end in any other building, and can go in either direction. Specifically, for any two buildings x and y, you can build either zero or one slides from x to y, and you can build either zero or one slides from y to x. The exception is that no slides are allowed to originate in building B, since once the CEO reaches that building, there is no need for her to do any more sliding.
In honor of Gooli becoming exactly M milliseconds old, the design must ensure that the CEO has exactly M different ways to travel from building 1 to building B using the new slides. A way is a sequence of buildings that starts with building 1, ends with building B, and has the property that for each pair of consecutive buildings x and y in the sequence, a slide exists from x to y. Note that the CEO is not requiring that any building be reachable from any other building via slides.
Can you come up with any set of one or more slides that satisfies the CEO's requirements, or determine that it is impossible?
Input
The first line of the input gives the number of test cases, T. T lines follow; each consists of one line with two integers B and M, as described above.
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1) and y is
the word POSSIBLE or IMPOSSIBLE, depending on whether
the CEO's requirements can be fulfilled or not. If it is possible, output an
additional B lines containing B characters each, representing a
matrix describing a valid way to build slides according to the requirements.
The j-th character of the i-th of these lines (with both i and j counting
starting from 1) should be 1 if a slide should be built going from
building i to building j, and 0 otherwise. The i-th character of
the i-th line should always be 0, and every character of the last
line should be 0.
If multiple solutions are possible, you may output any of them.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1 GB.
1 ≤ T ≤ 100.
Small dataset (Test Set 1 - Visible)
2 ≤ B ≤ 6.
1 ≤ M ≤ 20.
Large dataset (Test Set 2 - Hidden)
2 ≤ B ≤ 50.
1 ≤ M ≤ 1018.
Sample
3 5 4 2 1 4 20
Case #1: POSSIBLE 01001 00110 00001 00101 00000 Case #2: POSSIBLE 01 00 Case #3: IMPOSSIBLE
The sample outputs show one possible way to fulfill the specifications for each case. Other valid answers may exist.
Here is an illustration of the sample answer for Case #1:
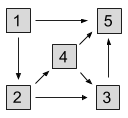
The four ways to get from building 1 to building 5 are:
- 1 to 5
- 1 to 2 to 3 to 5
- 1 to 2 to 4 to 5
- 1 to 2 to 4 to 3 to 5
In Case #3, building slides from 1 to 2, 2 to 3, 3 to 1, and 1 to 4 would create infinitely many ways for the CEO to reach building 4 (she could go directly to 4, or go around the loop once and then go to 4, or go around the loop twice...), but the CEO requested exactly 20 ways.
C. Fashion Police
Problem
You are so excited about the 2016 Code Jam World Finals that you just moved to New York. You have brought along J different jackets (numbered 1 through J), P different pairs of pants (numbered 1 through P), and S different shirts (numbered 1 through S). You have at least as many shirts as pairs of pants, and at least as many pairs of pants as jackets. (J ≤ P ≤ S.)
Every day, you will pick one jacket, one pair of pants, and one shirt to wear as an outfit. You wash all of your garments every night so all of your garments are available to use each day.
In New York, the Fashion Police officers are always watching and keeping track of what everyone wears every day. If they find out that you have worn the exact same outfit twice, you will immediately be taken to the Fashion Jail on 5th Avenue for a mandatory makeover; you definitely want to avoid that! You will also immediately be taken to Fashion Jail if they find out that you have worn the same two-garment combination more than K times in total. A combination consists of a particular jacket worn with a particular pair of pants, a particular jacket worn with a particular shirt, or a particular pair of pants worn with a particular shirt. For example, in the set of outfits (jacket 1, pants 2, shirt 3) and (jacket 1, pants 1, shirt 3), the combination (jacket 1, shirt 3) appears twice, whereas the combination (pants 1, shirt 3) only appears once.
You will wear one outfit per day. Can you figure out the largest possible number of days you can avoid being taken to Fashion Jail and produce a list of outfits to use each day?
Input
The first line of the input gives the number of test cases, T. T test cases follow; each consists of one line with four integers J, P, S, and K.
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1) and y is
an integer: the maximum number of days you will be able to avoid being taken to
Fashion Jail. Then output y more lines, each of which consists of
three integers: the numbers of the jacket, pants, and shirt (in that order) for
one day's outfit. The list of outfits can be in any order, but the outfits must
not cause you to go to Fashion Jail as described in the statement above.
If multiple answers are possible, you may output any of them.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1 GB.
1 ≤ T ≤ 100.
1 ≤ J ≤ P ≤ S.
1 ≤ K ≤ 10.
Small dataset (Test Set 1 - Visible)
S ≤ 3.
Large dataset (Test Set 2 - Hidden)
S ≤ 10.
Sample
4 1 1 1 10 1 2 3 2 1 1 3 2 1 2 3 1
Case #1: 1 1 1 1 Case #2: 4 1 1 2 1 2 3 1 2 1 1 1 1 Case #3: 2 1 1 2 1 1 1 Case #4: 2 1 1 3 1 2 1
The sample output displays one set of answers to the sample cases. Other answers may be possible.
In Case #1, even though the Fashion Police officers have set a lenient K value of 10, there is only one possible outfit that you can form, so you can only avoid Fashion Jail for one day.
In Case #2, adding any other outfit would cause you to go to Fashion Jail:
- Adding
1 1 3would use the combination (jacket 1, pants 1) more than 2 times. - Adding
1 2 2would use the combination (jacket 1, pants 2) more than 2 times.
In this case, any set of 5 outfits would include at least one fashion violation.
Note that the numbers of the jacket, pants, and shirt within an individual outfit do not have to be in nondecreasing order in the same way that J, P, and S do.
In Case #3, you have only one jacket + pants combination which you must keep reusing, so no matter which shirts you wear, you cannot form more than K = 2 different outfits.
In Case #4, another possible maximally large set of outfits is:
1 2 2
1 1 1
Analysis — A. Senate Evacuation
Test set 1
With at most three parties and at most nine senators, various brute force approaches will work. One exhaustive strategy is to generate all possible different evacuation orders, treating senators from the same party as interchangeable, and then try all possible different ways of chopping those into groups of one or two senators.
Another, simpler strategy is to keep randomly choosing and trying one of the nine possible evacuations (A, B, C, AA, AB, AC, BB, BC, CC) as long as the chosen senator(s) exist and the evacuation will not cause a new absolute majority. You may worry that this strategy could get stuck, but the outcome of any legal evacuation will just be another possible test case for the problem, and the statement guarantees that every test case has a solution! With more parties and senators, though, this strategy might bog down in the details of checking the legality of evacuations, so we should come up with a more efficient approach.
Test set 2
Intuitively, it is safest to remove one senator at a time, and to always draw from whichever party has the most remaining senators (or any such largest party, if there is a tie). But this strategy won't always work! For example, if we have two senators from party A and two from party B, and no others, which is a valid test case, then removing one senator from either party will give the other party an absolute majority.
However, this strategy is always safe whenever there are more than two parties present. Suppose that party 1 is currently the largest, or tied for the largest, of at least three parties, and that we remove a single senator from party 1. Clearly, making party 1 smaller cannot give it an absolute majority that it didn't have before. But could some other party acquire an absolute majority as a result? Suppose that the removal of a senator from party 1 were to cause party 2, which currently has X senators, to have an absolute majority. But since party 1 was the largest, or tied for the largest, before a senator was removed, party 1 must still have at least X-1 senators. Moreover, since at least one more party is present, there is at least 1 other senator who is not from party 1 or 2. So there are a total of at least X remaining senators who are not from party 2, which means the X senators of party 2 are not enough to give it an absolute majority, so we have a contradiction.
If we start with three or more parties and keep evacuating a single senator from the largest party in this way, then at some point, we must reach a step in which we go from three parties to two parties. These two remaining parties must have only one senator each. Since we just removed the one remaining senator from the third party, it must have been a largest party, so the other two can be no larger. So we can remove this last pair of senators in a single evacuation as a final step.
What if we start with two parties? Since the problem statement guarantees that no party begins with a majority, these parties must have equal numbers of senators. So, we can evacuate them in pairs, one from each party, until the evacuation is complete.
This approach takes more steps than are needed — most of those single evacuations can be paired up — but it gets the job done.
Analysis — B. Slides!
Slides!: Analysis!
Small dataset
The Small dataset has bounds that suggest we can construct all possible sets of slides, but this turns out to be overly optimistic. We represent a set of slides as a directed graph G, with each node representing a building, and a directed edge from node i to node j representing a slide leading from building i to building j. The most straightforward construction tries either including or not including each of the B * (B-1) possible slides, for a total of 2B * (B-1) possible sets of slides. Unfortunately, even for B = 6, this is too many: there are approximately 230 sets to check, or about a billion.
However, one observation allows us to dramatically cut down the number of sets we have to examine. Notice that there can never be a cycle as part of any valid path from building 1 to building B. If there were a cycle, then we could generate new, valid paths by traversing that cycle arbitrarily many times before continuing to our destination, meaning that the number of valid paths would be infinite. (The G that we use can still contain a cycle that is not on any valid path; however, removing that cycle would not affect the number of valid paths, and thus we only need to consider graphs G with no cycles at all.)
This means that any valid path from building 1 to building B cannot visit the same building twice, so each path can have length at most B. As a result, running a depth-first search on G starting from node 1 will take O(B) time for each path found. If we find more than M paths, then we can terminate our search immediately, since this set of slides cannot be valid. This means that our worst-case running time to test any given set of slides is O(M*B). We can also calculate a smaller upper bound on the number of sets we have to examine: for each pair of slides i and j, exactly one of three possibilities must be true:
- There is a slide from i to j.
- There is a slide from j to i.
- There is no slide from i to j and no slide from j to i.
Since there are B * (B-1) / 2 different pairs of slides, this gives us an upper bound of 3B * (B-1) / 2 possible sets of slides. For B = 6, this number is around fourteen million, which is a manageable number of sets to check.
Another helpful observation that makes the small even more tractable is that since our graph has no cycles, it is a directed acyclic graph, and so it has a topological sorting. So, for any correct solution, we could renumber the buildings (other than 1 and B) such that every slide's end building has a larger number than its start building. Since this is true, we only need to consider slides that go from lower to higher building numbers.
Large dataset
The Large dataset requires a more efficient approach. A natural first question to ask is: what is the maximum number of paths from building 1 to building B that we can possibly construct? One straightforward construction that seems to yield a large number of paths is to construct a slide from building i to building j for every pair of positive integers i, j with 1 ≤ i < j ≤ B. To compute the number of paths for this set of slides, notice that every path from building 1 to building B corresponds uniquely to a set of distinct integers from the set {2, ..., B-1} representing the buildings visited along that path. For example, if B = 5, then the set {2, 4} would correspond to the path 1 -> 2 -> 4 -> 5, and the empty set would correspond to the path 1 -> 5. Since there are B-2 integers strictly between 1 and B, each of which can be either absent or present in a set, there are 2B-2 unique sets that can be constructed, and thus 2B-2 possible paths from 1 to B.
But is this the largest possible number of paths we can construct? It turns out that it is. We can show this by the pigeonhole principle. We assume that there exists some set of slides that yields some number M > 2B-2 paths, and derive a contradiction. Each path corresponds to some set of distinct integers {2, ..., B-1} representing the buildings visited along that path, and since there are 2B-2 distinct such sets, it follows that two paths of slides must visit the exact same buildings. This means there is some pair of buildings i and j such that i is visited before j on one of these paths, but is visited after j on the other path. (If there were no such pair, then these two paths would be exactly the same, since no building can ever be visited twice.) Since we can reach building i from building j and vice versa, it follows that there is a cycle between the two buildings. This contradicts what we showed earlier, meaning that we cannot construct a set of slides with exactly M paths for M > 2B-2.
Now we show how to extend the ideas above to handle the case where M < 2B-2. We start by constructing all possible slides from building i to building j for every pair of positive integers i, j with 2 ≤ i < j ≤ B. Notice that there are exactly 2B-1-i ways to get from building i to building B. Each path from building i to building B maps uniquely to a subset of distinct integers from the set {i + 1, ..., B-1}. This set contains B-1-i integers, so there are 2B-1-i possible subsets that we can choose. If we build a slide from building 1 to building i for i strictly between 1 and B, then this increases the number of ways to get from 1 to B by exactly 2B-1-i, since there are that many ways to get from building i to building B. This suggests a method for generating a network with exactly M slides. We start by writing M in binary. If the i-th digit of M (counting from the right, starting from 1) is a 1, then we add a path between building 1 and building B-i. This will add 2i-1 new paths to our slide network. If we repeat this process for each value of i, then we will end up with a network with a number of paths from 1 to B exactly equal to M. This process will work if M has at most B-2 digits, meaning M ≤ 2B-2-1. Since M = 2B-2 is the largest value we are able to construct, this gives us a method for constructing all values of M between 1 and 2B-2. We have previously shown a construction for M = 2B-2, which is equivalent to the solution for M = 2B-2 - 1 with an additional path from building 1 to building B.
This means that a sequence of slides is therefore possible to construct if, and only if, M ≤ 2B-2, and the above construction works for any such M. The sequence itself is computed by the construction above.
To illustrate the above method, here are valid answers for all cases with B = 5, and M = 1 through 8:
M = 1 M = 2 M = 3 M = 4 M = 5 M = 6
M = 7 M = 8
00010 00100 00110 01000 01010 01100 01110 01111
00111 00111 00111 00111 00111 00111 00111 00111
00011 00011 00011 00011 00011 00011 00011 00011
00001 00001 00001 00001 00001 00001 00001 00001
00000 00000 00000 00000 00000 00000 00000 00000
Observe that the solutions only differ in their first lines. The first lines of
the solutions for M = 1 through 7 are 1, 2, ..., 7 in binary plus an
extra 0 at the end. The first line of the solution for M = 8 is 7 in
binary, plus an extra 1 at the end: the direct connection from building 1 to
building 5 that brings the total to 8. For M ≥ 9, the answer is
IMPOSSIBLE.
Analysis — C. Fashion Police
Fashion Police: Analysis
Small dataset
Let us denote the number of possible outfits by W; W = J * P * S. A viable brute force approach is to produce all 2W subsets of the set of possible outfits, check them for violations, and take one of the largest sets with no violation. We can check a set of outfits without worrying about what order they are worn in; if some outfits in that set create a fashion violation, it will eventually happen no matter what order those outfits (and any other outfits) are worn in. Another helpful observation is that if S ≤ K, then the answer is trivial: simply return every possible outfit.
This approach works for most of the Small cases, but not all of them. For
the cases 3 3 3 1 and 3 3 3 2, there are
227 possible sets of outfits, and that is over 100 million. One
approach is to just solve these "problem cases" before downloading a dataset.
You can notice a pattern in the other answers (more on this later) and infer
that the maximum numbers of outfits you can wear are 9 and 18, respectively.
It is more tractable to find a set of outfits of a particular size than to
find the set of outfits of maximum size. If you are pretty sure that that size
is 18, for instance, you can check all sets of size 18 until you find a working
one, and maybe even check all sets of size 19 to confirm that none of them
work. This is much faster than checking every size between 1 and 19, especially
since 27 choose 18 is much smaller than 27 choose 13 and 27 choose 14, for
example.
In fact, there are only 100 possible test cases that fall within the limits of the Small dataset, so you can compute the answer to any possible input before even downloading the dataset!
Large dataset
Again, if S ≤ K, we can return every possible outfit. Otherwise, a key insight is that that the pigeonhole principle tells us that a maximum solution can have no more than min(J × P × K, P × S × K, J × S × K) different outfits. Since J ≤ P ≤ S, this puts an upper bound of J × P × K on our solution. You can also infer this from the output of a brute force solution.
One pitfall to watch out for in this problem is that there exist sets of outfits that are maximal — that is, you cannot add any new outfit to such a set without going to jail — but are not the largest possible. That is, they are maximal but not maximum.
For instance, for an input of J = 1, P = 3,
S = 3, K = 2, the following is a maximal set of
outfits that is not maximum (the maximum size is 6): 1 1 1,
1 1 2, 1 2 2, 1 2 1, 1 3 3.
So, if we just randomly choose outfits without violating the law, we are in danger of being trapped in a locally maximal set.
Fortunately, there are several greedy approaches to achieve a set of size J × P × K outfits without angering the Fashion Police. As argued above, we know that J × P × K is the maximum possible size, so if we can find a set of that size, we are done!
We cannot use a jacket-pants combination more than K times, so if we want to produce J × P × K outfits we are forced to use each combination exactly K times. To simplify the math, we use jacket, pants and shirt numbers between 0 and the appropriate total minus 1. We just need to remember to add 1 to every identifier when we print it to the output.
Let us fix a combination with jacket number j and pants number p. Our proposal is assign to it shirts (j + p) % S, (j + p + 1) % S, ..., (j + p + K - 1) % S, where % stands for the modulo operation. Since S > K, these are all different, and by construction, the combination of jacket and pants is used exactly K times, as desired.
What about jacket-shirt and pants-shirt combinations? Let us fix a jacket number j and a shirt number s. If the outfit (j, p, s) appears in the constructed set, then s = (j + p + d) % S for some d between 0 and K - 1, inclusive. Then, by modular arithmetic, and noticing that j % S = j, p % S = p, and s % S = s, it turns out that p = (s - j - d) % S. Then, each choice of d uniquely determines p, so there cannot be more ps to go with a given combination of j and s than choices of d, and there are K choices of d, which means the combination of j and s does not exceed the maximum.
Since this is valid for any j and s, and a symmetrical proof is valid for each pants-shirt combination, we have proven that the proposed set of outfits does not break any of the rules of the Fashion Police.
Another way of thinking about it
The problem is equivalent to trying to select as many cells as possible in a 3-D J by P by S grid such that no line of three cells in the x, y, or z direction includes more than K selected cells. Each outfit corresponds to one such cell.
Here is an illustration of this approach for two cases. The left-right axis
corresponds to shirts, the up-down axis corresponds to pants, and the layers
(imagine them stacked up) correspond to jackets. Each * represents
a selected outfit, and each . represents an unused outfit.
J = 2, P = 3, S = 4, K = 1:
*... .*..
.*.. ..*.
..*. ...*
Outfits: 1 1 1, 1 2 2, 1 3 3,
2 1 2, 2 2 3, 2 3 4.
J = 2, P = 3, S = 4, K = 2:
**.. .**.
.**. ..**
..** *..*
Outfits: 1 1 1, 1 1 2, 1 2 2,
1 2 3, 1 3 3, 1 3 1, 2 1 2,
2 1 3, 2 2 3, 2 2 4, 2 3 4,
2 3 1.
Observe that:
- In both cases, the second layer (jacket 2) is the first layer (jacket 1) shifted one unit to the right (and wrapping around).
- We can get the answer to the second case from the answer to the first case
just by adding a
*to the right of every existing*(and wrapping around). - By construction, the first layer does not have more than K
*s in any row or column. This is also true of each additional layer, since they are all rotations of the first layer. Moreover, no line of cells parallel to the jacket axis (that is, across layers) can possibly have more than K*s; considering how the layers are constructed, that would directly imply more than K*s in one row of the first layer.
This construction works for any set of J, P, and S values. It takes advantage of the J ≤ P ≤ S condition in the problem statement. We put that condition in to save you the trouble of adding a bunch of case-based logic to try to figure out which dimension was largest; the fashion-conscious GCJ staff is well aware that some closets have more pants than shirts!