Google Code Jam Archive — Round 1B 2016 problems
Overview
Round 1B featured two problems with possible greedy approaches, Getting the Digits and Close Match; the latter was much trickier to wrestle with! Technobabble required bipartite matching for the Large; more advanced techniques like this tend to show up as the contest goes on.
Two of our competitors in Round 1B, ikatanic and rng..58, accomplished a feat that we've never seen before in Code Jam: by submitting their final correct datasets at exactly the same time (37 minutes and 32 seconds into the contest, with no penalties for wrong Smalls), they tied for first place! Congratulations to our co-winners of this round.
Almost 8,000 contestants submitted at least one correct dataset, and there were 324 perfect scores. To be in the top 1000, you needed at least 56 points (which usually meant at least two Larges) plus some speed.
The top 1000 contestants in this round advance to Round 2 and Distributed Round 1, joining the 1000 advancers from Round 1A. We will email official results early next week. If you weren't in the top 1000 in Rounds 1A or 1B, Round 1C will give you one more chance to advance; see the schedule.
Cast
Problem A (Getting the Digits): Written by Ian Tullis. Prepared by Steve Thomas and Ian Tullis.
Problem B (Close Match): Written by Pablo Heiber. Prepared by Karol Pokorski and Ian Tullis.
Problem C (Technobabble): Written by Ian Tullis. Prepared by John Dethridge and Karol Pokorski.
Solutions and other problem preparation and review by Shane Carr, John Dethridge, Minh Doan, Jackson Gatenby, Taman (Muhammed) Islam, Timothy Loh, Karol Pokorski, Steve Thomas, and Yerzhan Utkelbayev.
Analysis authors:
- Getting the Digits: Ian Tullis
- Close Match: Ian Tullis
- Technobabble: Shane Carr
A. Getting the Digits
Problem
You just made a new friend at an international puzzle conference, and you asked for a way to keep in touch. You found the following note slipped under your hotel room door the next day:
"Salutations, new friend! I have replaced every digit of my phone number with its spelled-out uppercase English representation ("ZERO", "ONE", "TWO", "THREE", "FOUR", "FIVE", "SIX", "SEVEN", "EIGHT", "NINE" for the digits 0 through 9, in that order), and then reordered all of those letters in some way to produce a string S. It's up to you to use S to figure out how many digits are in my phone number and what those digits are, but I will tell you that my phone number consists of those digits in nondecreasing order. Give me a call... if you can!"
You would to like to call your friend to tell him that this is an obnoxious way to give someone a phone number, but you need the phone number to do that! What is it?
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each consists of one line with a string S of uppercase English letters.
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1) and y is
a string of digits: the phone number.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1 GB.
1 ≤ T ≤ 100.
A unique answer is guaranteed to exist.
Small dataset (Test Set 1 - Visible)
3 ≤ length of S ≤ 20.
Large dataset (Test Set 2 - Hidden)
3 ≤ length of S ≤ 2000.
Sample
4 OZONETOWER WEIGHFOXTOURIST OURNEONFOE ETHER
Case #1: 012 Case #2: 2468 Case #3: 114 Case #4: 3
B. Close Match
Problem
You are attending the most important game in sports history. The Oceania Coders are playing the Eurasia Jammers in the Centrifugal Bumble-Puppy world finals. Unfortunately, you were sleep deprived from all the anticipation, so you fell asleep during the game!
The scoreboard is currently displaying both scores, perhaps with one or more leading zeroes (because the scoreboard displays a fixed number of digits). While you were asleep, some of the lights on the scoreboard were damaged by strong ball hits, so one or more of the digits in one or both scores are not being displayed.
You think close games are more exciting, and you would like to imagine that the scores are as close as possible. Can you fill in all of the missing digits in a way that minimizes the absolute difference between the scores? If there is more than one way to attain the minimum absolute difference, choose the way that minimizes the Coders' score. If there is more than one way to attain the minimum absolute difference while also minimizing the Coders' score, choose the way that minimizes the Jammers' score.
Input
The first line of the input gives the number of test cases, T. T cases follow. Each case consists of one line with two non-empty strings C and J of the same length, composed only of decimal digits and question marks, representing the score as you see it for the Coders and the Jammers, respectively. There will be at least one question mark in each test case.
Output
For each test case, output one line containing Case #x: c j, where
x is the test case number (starting from 1), c is
C with the question marks replaced by digits, and j is
J with the question marks replaced by digits, such that the absolute
difference between the integers represented by c and
j is minimized. If there are multiple solutions with the same
absolute difference, use the one in which c is minimized; if there
are multiple solutions with the same absolute difference and the same value of
c, use the one in which j is minimized.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1 GB.
1 ≤ T ≤ 200.
C and J have the same length.
Small dataset (Test Set 1 - Visible)
1 ≤ the length of C and J ≤ 3.
Large dataset (Test Set 2 - Hidden)
1 ≤ the length of C and J ≤ 18.
Sample
4 1? 2? ?2? ??3 ? ? ?5 ?0
Case #1: 19 20 Case #2: 023 023 Case #3: 0 0 Case #4: 05 00
In sample case #4, note that the answer cannot be 15 10; that
minimizes the absolute difference, but does not minimize the Coders' score.
Nor can the answer be 05 10; that minimizes the absolute
difference and the Coders' score, but does not minimize the Jammers' score.
C. Technobabble
Problem
Every year, your professor posts a blank sign-up sheet for a prestigious scientific research conference on her door. If a student wants to give a lecture at the conference, they choose a two-word topic that is not already on the sheet and write it on the sheet. Once the deadline has passed, the professor has one of her grad students put the topics in a random order, to avoid biasing for or against students who signed up earlier. Then she presents the topics to you for review.
Since the snacks at the conference are excellent, some students try to fake their way into the conference. They choose the first word of some topic already on the sheet and the second word of some topic already on the sheet, and combine them (putting the first word first, and the second word second) to create a new "topic" (as long as it isn't already on the sheet). Since your professor is open-minded, sometimes this strategy actually works!
The fakers are completely unoriginal and can't come up with any new first or second words on their own; they must use existing ones from the sheet. Moreover, they won't try to use an existing first word as their own second word (unless the word also already exists on the sheet as a second word), or vice versa.
You have a list of all N of the submitted topics, in some arbitrary order; you don't know the order in which they were actually written on the sheet. What's the largest number of them that could have been faked?
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each consists of one line with an integer N, followed by N lines, each of which represents a different topic and has two strings of uppercase English letters: the two words of the topic, in order.
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1) and y is
an integer: the largest number of topics that could have possibly been faked.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1 GB.
1 ≤ T ≤ 100.
1 ≤ length of each word ≤ 20.
No topic is repeated within a case.
Small dataset (Test Set 1 - Visible)
1 ≤ N ≤ 16.
Large dataset (Test Set 2 - Hidden)
1 ≤ N ≤ 1000.
Sample
3 3 HYDROCARBON COMBUSTION QUAIL BEHAVIOR QUAIL COMBUSTION 3 CODE JAM SPACE JAM PEARL JAM 2 INTERGALACTIC PLANETARY PLANETARY INTERGALACTIC
Case #1: 1 Case #2: 0 Case #3: 0
In sample case #1, one possibility is that the topics were added to the sheet in this order:
QUAIL BEHAVIOR (real)
HYDROCARBON COMBUSTION (real)
QUAIL COMBUSTION (fake)
There is no scenario in which more than one of the topics can be fake.
In sample case #2, all of the topics must be real. Whatever order they were written in, at no point would it have been possible to use existing words to create a new topic that was not already on the list.
In sample case #3, neither topic can be fake. For example, if
INTERGALACTIC PLANETARY had been the first and only topic written
on the sheet, a faker could only have used INTERGALACTIC as the
first word of a new topic and could only have used PLANETARY as
the second word of a new topic... but the only topic that the faker could have
formed would have been INTERGALACTIC PLANETARY, which would have
been off limits since it was already on the sheet. So
PLANETARY INTERGALACTIC must have also been a real topic.
Analysis — A. Getting the Digits
Getting the Digits: Analysis
Small dataset
Since the string can be no longer than 20 letters in the Small dataset, the
phone number can be no longer than six digits (since the digits with the
shortest spelled-out length, ONE and TWO, have three
letters, and 7 * 3 > 20). A key observation is that this means there are no
more than a million possible answers; in fact, there are far fewer than that,
since only phone numbers with digits in nondecreasing order are valid.
So, you can look at all possible phone numbers from 0 to
9, 00 to 99 (note that 00
is different from 0), and so on, up to 000000 through
999999, and save the numbers that have their digits in
nondecreasing order. (In fact, for that last range, you only need to go up to
222222.) Then, turn each of those into letters. There are
multiple possible orderings for those letters — 1 could be
given as EON, ENO, or NEO, among others
— but you can just take the alphabetically ordered version. 0
becomes EORZ, 1 becomes ENO, ...,
01 becomes EENOORZ, and so on.
Then you can make a dictionary (hash table) with these strings as keys and the phone numbers as values. (It turns out that each of those keys maps to only one phone number — more on that later.) To solve a test case, take the string your friend gave you, sort it alphabetically, and then look that up in the dictionary. (Your friend could have given you the same string in any order, so you can permute it however you want without changing the identity of the underlying phone number.)
There's no need to generate this dictionary every time you solve a test case; you can do it just once, before your program starts processing test cases. You can even produce the entire dictionary before you download an input file and store it in your source code or in a separate file that your source code reads, as long as this does not cause your source code to exceed the standard limit of 100kB.
Large dataset
The dictionary for all 1000-digit phone numbers would be too huge to generate and store beforehand, let alone produce on the fly.
One tempting approach is to greedily remove spelled-out digits: for instance,
keep taking the letter set NINE (one E, one
I, and two Ns) away until you no longer can, then
keep taking the letter set EIGHT away, and so on. But this won't
necessarily work — what if there are no 9s in the actual
phone number, and the first NINE you try to take away is really
the N from a SEVEN, the I from a
SIX, and the NE from a ONE? This will
eventually leave you with a mess of letters from which no digit's letters can
be removed!
It turns out that you can make this method work... as long as you pick the
right order in which to remove the digits! For instance, FOUR is
the only digit out of the ten that contains a U. So, if you see
three Us in the string, there must be three instances of
FOUR. You can safely remove three Fs, three
Os, three Us, and three Rs, and record
that the phone number has three 4s. Once all the
FOURs are gone, FIVE is the only remaining digit with
an F, so you can remove as many FIVEs as there are
Fs, and so on. If you had tried to do this in the other order,
starting by removing as many FIVEs as there were Fs,
it might not have worked, depending on how many FOURs,
SIXes, SEVENs, etc. were in the number!
Here is one safe order in which to remove digits, based on their letters that
are unique at the time of removal: ZERO,
SIX, EIGHT, TWO,
FOUR, FIVE, SEVEN,
THREE, NINE, ONE.
Note, for example, that even though all of the letters in ONE
appear in other digits besides ONE, by the time we get to removing
ONEs, there are only ONEs left.
The existence of an ordering like this also explains why we didn't have to
worry about two different phone numbers having the same alphabetized string in
our dictionary for the Small solution. Two different phone numbers cannot
produce the same string because no subset of digit words is a linear
combination of other digit words. This would not necessarily hold for
arbitrary sets of words, though. For example, in a language in which the digit
words are AB, AC, BD, and
CD, given the string ABCD, it is impossible to know
whether it was formed from one AB and one CD, or from
one AC and one BD.
Analysis — B. Close Match
Close Match: Analysis
Small dataset
A brute force algorithm will work just fine for the Small. For each case, we
can try all possible ways to fill in the ?s and see which way
produces the smallest absolute difference. It is important to break any ties
first by the first score, or, if necessary, by the second score. Even in the
worst case for brute force, ??? ???, there are only 106
= one million different possibilities to check.
Large dataset
Many Code Jam problems look complex and challenging, but have a surprisingly simple solution. But sometimes we throw in just the opposite sort of problem! In this case, it's easy to come up with a tantalizing greedy approach that will sometimes fail. We'll present an approach that gets greedy only when it's safe to do so.
We will investigate various different ways to fill in the ?s, and
we will constantly keep track of the best set of scores (using tiebreaker
rules) seen so far. We will look at the pair of characters in the first
position of each string, then the pair of characters in the second position of
each string, and so on.
When we look at a pair of characters, we must decide how to fill in any
?s. We may be able to make those two digits of the final scores be
the same, either by filling in ?s appropriately, or because the
two characters are already the same digit and we have no choice. If we're
lucky, and we never encounter a position where the two strings have different
digits, we can make every pair of digits in the final scores the same! This is
as good as it gets; our difference will be 0.
For example, for the case ?1? 2??, we can make all the digits
equal to get 210 210. We choose 0s for any pair of
?s to satisfy the tiebreaker rules.
However, we won't have this option in every test case. If the strings have
different digits at some position, then there's no way the score difference
can be 0. Moreover, we may even need to introduce our own difference before
that first existing point of difference! For instance, in the case ??0
?99, we don't want to just make the digits equal until we get to the
first point of difference, because that would leave us with
090 099, whereas we can do better with 100 099.
So, if we have two different digits at any position in the strings, then either we can make everything equal up to that first existing point of difference, or we can introduce a first point of difference earlier. That is, we will start from the left, and for some number of positions (possibly zero), we will make the digits in the final scores equal. Then we will encounter (or make) our first point of difference.
Once we've reached our first point of difference, we know something crucial:
which of the two final scores is larger. Because the scores have been
equal up until the first point of difference, the score with the larger digit
in this position is guaranteed to be larger, no matter how we fill in any
?s beyond this point.
Moreover, we know exactly how to fill in those ?s to minimize the
difference between the two scores! We have no reason to make the larger number
any larger, so all of its ?s should become 0s. And we
want to make the smaller number as large as possible, so all of its
?s should become 9s.
So, as we step through our strings from left to right, for every position of the strings, we'll do the following:
- If we encounter two identical digits, move on.
- If we encounter two different digits, fill in all remaining
?s, compare those scores with the best we've seen so far, and stop. We're done! - If we encounter a digit and a
?:- If the digit is not
9: try changing the?to 1 more than that digit. This would introduce a first point of difference, so we know how we would fill in all remaining?s. Compare those scores with the best we've seen so far. Then... - If the digit is not
0: try changing the?to 1 less than that digit. This would introduce a first point of difference, so we know how we would fill in all remaining?s. Compare those scores with the best we've seen so far. Then... - Change the
?to that digit and move on. (Why didn't we try changing the?to all possible digits? We can get away with doing this, but it's not necessary. If we have control over the digits at the first point of difference, there's no reason to make them differ by more than 1; this would just make the overall difference larger, regardless of what we do with the rest of the strings.)
- If the digit is not
- If we encounter two
?s:- Try changing the first
?to a0and the second?to a1. Figure out the scores and compare. Then... - Try changing the first
?to a1and the second?to a0. Figure out the scores and compare. Then... - Change both
?s to 0s and move on. (Again, there is no reason to make the?s differ by more than1.)
- Try changing the first
We must make sure our implementation also checks the case in which there is no point of difference. Once we're done, the best scores will be our answer.
This approach has some room for improvement, but it solves the Large very quickly. It makes one full pass through the strings, and at each position, it might make up to 2 additional partial passes, so the worst case running time is O(N2), where N is the length of C (and J). We leave an O(N) approach as an exercise!
Analysis — C. Technobabble
Technobabble: Analysis
Small dataset
Each topic on the list could be "faked" or "un-faked." One natural brute force solution is to enumerate all possible orderings of the topics, and pick the one that has the most faked topics.
It's easy to check whether a topic could have been faked: simply check whether the first word of the topic appears as a first word earlier in the list, and the second word of the topic appears as a second word earlier in the list. Note that marking a topic as faked does not change whether or not topics later in the list can be marked as faked, so using this strategy, it is optimal to always count a topic as faked if possible.
However, there are N! possible orderings, which is too large to enumerate even for the small dataset where N ≤ 16 (16! is on the order of 21 trillion). We need a better approach. Rather than trying to maximize the number of faked topics, let's think about the reverse problem: trying to minimize the number of un-faked topics.
The key observation is that any possible set of un-faked topics must contain every first word at least once and every second word at least once — otherwise, there would be a faked topic that contained a word that was not available for the faker to use. Conversely, any set containing every first word at least once and every second word at least once could be a possible set of un-faked topics — simply put all the topics from the un- faked set at the top of the list. So, the question we need to answer is this: What is the smallest set of topics that contains every first word at least once and every second word at least once?
A brute-force approach, which works for the Small dataset, is to enumerate all subsets of topics and pick the subset with the fewest topics that covers every first word at least once and every second word at least once. Since there are 2N subsets, this solution runs in exponential time, which is fine for the Small dataset (216 = 65,536).
Large dataset
For the large dataset, the exponential time solution will not work. It turns out that there is a polynomial time solution to the problem. We will illustrate the solution using graph theory.
Let each word be a vertex in a bipartite graph in which each topic is an edge connecting two vertices. The sample input below corresponds to the following graph (we'll explain the colors of the edges in a moment).
HYDROCARBON COMBUSTION
BIOMASS COMBUSTION
QUAIL COMBUSTION
QUAIL BEHAVIOR
QUAIL CONTAMINATION
GROUNDWATER CONTAMINATION
GROUNDWATER HYDROLOGY
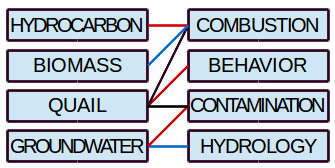
The problem we're trying to solve on this graph is the minimum edge cover; that is, finding the smallest set of edges such that each vertex is connected to at least one edge. This corresponds to the smallest set of topics containing every first word at least once and every second word at least once.
The minimum edge cover problem is related to finding a maximum matching of a graph (the largest set of edges without any common vertices): the two will always have the same number of connected components. If it's not immediately obvious why this is the case, convince yourself by drawing some graphs on paper and trying to come up with a counter-example. We can additionally observe that every vertex left out of a maximum matching must be connected to a vertex in the maximum matching; otherwise, we could have added that pair to the maximum matching. With these facts, we can use a two-step algorithm to compute a minimum edge cover on our bipartite graph:
- Find a maximum cardinality bipartite matching of the graph, which can be done in polynomial time using an approach such as the Ford-Fulkerson algorithm or the Hopcroft–Karp algorithm. One such matching is shown above in red.
- Iterate over the remaining edges, and greedily add edges that connect to an unused vertex. The edges added by this step are shown above in blue.
In fact, all we really need to know is the size of a minimum edge cover: the number of edges in a maximum matching plus the number of vertices not included in a maximum matching. The solution to the problem is then simply the total number of edges (topics) minus the size of a minimum edge cover.