Google Code Jam Archive — Round 1A 2016 problems

The Last Word: Analysis

Small dataset

In the Small dataset, there will be at most 15 letters in S. At each step of the game, we are given a letter to add to either the front or the back of the current word. The number of possible words after adding the i-th letter (during step i) is at most twice the number of possible words after step i-1, since we have two choices of where to add the new letter. This means that the number of possible last words that can be made from all of the letters is at most 2¹⁵. We can generate each of these possible last words and find which one comes last alphabetically.

Here is one way of doing this in Python:

def alphabetically_last_word(S):
  possible_words = set([''])
  for c in S:
    possible_words = set([c + r for r in possible_words] + [r + c for r in possible_words])
  return max(possible_words)

Large dataset

The approach in the previous paragraph is too slow for the Large dataset, and so some additional observations are required. During step i, we are adding a single new letter S_i to the front or the back of our current word X_i-1, yielding a new word X_i = X_i-1S_i or X_i = S_iX_i-1. To have the end result be as alphabetically late as possible, it is always better to have X_i be as alphabetically late as possible as well. We can show this formally: during every step of the process that produces the alphabetically latest answer, after i letters have been chosen, our string X_i should be the alphabetically latest substring that we can produce from the first i letters of S under the given rules.

Assume we are at the i-th step, and we can either add the new letter S_i at the beginning or the end of X_i-1. Let Y_i be the alphabetically earlier of S_iX_i-1 and X_i-1S_i, and Z_i be the alphabetically later of the two. Suppose that Y_i were the optimal choice at this step. Then we could write our last word as AY_iB for some A and B. We could instead choose Z_i and insert the letters during future steps in the same way to yield AZ_iB as the last word. No matter what the values of A and B are, it is always true that AZ_iB comes no alphabetically earlier than AY_iB, because Z_i comes no alphabetically earlier than Y_i. This means that any word using Y_i can be turned into a word that is at least as late in alphabetical order by substituting Z_i at this step instead. It follows that choosing Z_i is always correct.

This means that our X_i must be the alphabetically latest of X_i-1S_i and S_iX_i-1. Therefore, when we add S_i to X_i-1, we only need to check whether putting S_i in the front or putting S_i in the back would produce the alphabetically latest string.

Here is some simple Python code that implements the optimized procedure:

def alphabetically_last_word(S):
  result = ''
  for c in S:
    result = max(c + result, result + c)
  return result

Note that the solutions for the Small and Large datasets are very similar. The only difference is that the solution to the Large recognizes which one of the possible words that can be formed at each step will necessarily be part of the optimal last word. Instead of keeping an amount of information that may grow exponentially with the number of steps in the game, the code for the Large keeps track of a single string at each step, allowing it to run much faster and use less memory. The presented solution for the Small dataset requires exponential time and memory, whereas the presented solution for the Large dataset requires only polynomial time and memory.

Another way to think about this is that the max operation commutes with the set-building step inside the code for the Small, allowing us to keep the maximum at each step rather than computing the maximum at the end. This observation shows a path for extending a solution that solves the Small dataset into the one we explained that can also solve the Large dataset. (Check out "A possible stepping stone..." in this essay.)

Rank and File: Analysis

Small dataset

A natural first approach is to reconstruct the grid by brute force: try all ways of assigning the lines to the rows and columns until the lines all overlap perfectly, with no conflicts. But as we get into later rounds of Code Jam, pure brute force becomes less likely to work for every Small dataset! In this case, with N = 10, we can have up to 19 lines that we must turn into a 10 x 10 array. Trying all 20! = about 2.4 * 10¹⁸ ways of assigning those 19 lines (plus the one empty line that we need to figure out) to the 20 rows and columns would just take too long, and Sergeant Argus isn't going to give us that much time.

Here's one approach that takes advantage of the unusual properties of the grid. Let's continue with our 19-line case. We'll assume (without loss of generality) that the grid has a column missing. In that case, our grid has 10 rows. We can try all 19 choose 10 = 19! / (10! * 9!) = 92378 ways of choosing ten of our lines to call the "rows". But what order should they go in? Well, we know that the values in the first column, like the values in any other column, must be in strictly increasing order. If any two of the "rows" that we've chosen begin with the same number, then we must not have chosen the right set, and we can move on. Otherwise, we know exactly how to order them, so we already have a complete potential grid! Then we can just check the 10 columns to see if 9 of them match the 9 lines we didn't use in this set. If they do, then the remaining line is the answer.

Large dataset

With up to 99 lines, the approach above won't work: 99 choose 50 is roughly 5 * 10²⁸.

It is possible to write a solution that reconstructs such a large grid. But it turns out that we don't need to frame the problem that way at all! We haven't fully taken advantage of the fact that we're only asked for the missing row or column, not for the entire grid.

In a complete set of lists of rows and columns of a grid, every cell of the grid appears twice: once in the list for the row it is in, and once in the list for the column it is in. There may be multiple copies of the same number in the grid, but we can still say that every number appears an even number of times in total within that complete set of lists.

But what about our input set of lists, which is missing the list for one row or column? All of the numbers in that missing list are different, and each of them appears one time fewer in the input than it would in the complete set of lists. This means that all of those numbers appear an odd number of times in our input. Moreover, they are the only numbers that appear an odd number of times in our input!

Therefore, we don't need to build a grid at all. All we need to do is look through all the numbers in all the lists and see which N of them appear an odd number of times; those are the numbers in our missing row/column. We can put them in the order they must go in (strictly increasing), and then we have our answer. And we haven't even done a single push-up!

BFFs: Analysis

Small dataset

The Small dataset has a pretty low limit of 10 kids. That allows us to try every possible arrangement and check which ones would make valid circles (circles in which every kid is next to their BFF). For every possible subset of kids and every possible circular ordering of them, check that for every kid at least one of their neighbors is a BFF, and if that is the case, update a running global maximum if it is greater than the size of the circle we just checked.

There are a number of small but powerful optimizations to this approach. Notice that the permutations of a subset of kids S always appear as a prefix of the permutations of any other subset of kids that includes S. Moreover, the only difference in BFF checking is what we do for the first and last kid. So, we can just check all the permutations of N kids and consider whether each prefix forms a valid circle, and that accounts for all permutations of all subsets while reducing the number of total checks substantially. Note that some subsets are checked multiple times, but that is unimportant, as long as the procedure runs in the allotted time.

There are other possible optimizations, but this is more than enough. The following Python code implements the approach outlined above:

import itertools
# The F parameter is the list of BFF identifiers, but 0-based (subtracting 1 from the input).
def cc(F):
  n = len(F)
  r = 0
  # Iterate over all possible orderings of the n kids.
  for O in itertools.permutations(xrange(n)):
    first = O[0]
    second = O[1]
    for i in xrange(1, n):  # Iterate over the permutation, skipping the first.
      # Check if i can be the last one by checking it and the first.
      prev = O[i - 1]
      cur = O[i]
      if ((F[cur] == first or F[cur] == prev) and
          (F[first] == cur or F[first] == second)):
        r = max(r, i + 1)
      # Check if i can be in the middle, and stop if it can't.
      if F[cur] != prev and (i == n - 1 or F[cur] != O[i + 1]):
        break
  return r

Large dataset

Of course, a simple brute force approach, even with many additional optimizations, will not be fast enough for the Large dataset. Let's examine the input more closely. It is actually a function BFF that maps each kid to another kid. We can represent this function with a graph where the nodes are kids and the edges go from each kid to that kid's BFF. As you can see from the linked article, this type of graph has a particular property: each connected component is made up of a directed cycle and branches of nodes with the edges directed towards the cycle. To visualize it better, if we compressed the cycle into a single node, we would obtain a tree with all the edges pointing towards the root. Here's an important fact that will come up a lot: each connected component contains exactly one cycle.

Now that we have examined the input a bit, let's examine the output, or, better yet, let's examine the form of a valid circle. It must contain at least one kid k₁. It must also contain k₁'s BFF, k₂, who must be sitting next to k₁. And k₂'s BFF k₃ (who might or might not be k₁), and so on. The BFF of the BFF of the BFF ... of k₁ must be in the circle. In terms of the graph we mentioned above, we are starting on the node representing the first kid k₁, and moving through the edges. Therefore, we will eventually end up cycling through the cycle in k₁'s connected component. (That cycle may or may not include k₁.) This a second important property: for any connected component containing at least one kid who is in the circle, all of the kids in that component's cycle must be in the circle..

Consider a connected component with a cycle of more than 2 kids. If we put that cycle in the circle, there is no room for anyone else, as the cycle already forces the two neighbors of each kid. So, one possibility is that the final circle consists entirely of a single cycle from the graph.

Since nobody is their own BFF, there are no cycles with just 1 kid. If we consider a connected component with a cycle of exactly 2 kids l and r, the situation is different. We can sit l and r together, and we already know they are both happy, and we have room on l's left and r's right (or vice versa, but it is equivalent) to seat more kids. We could choose anybody, even from another component. However, we want the maximum number of kids, so we might as well choose an l₁ whose BFF is l to sit next to l (if there exists such an l₁). l₁ is already happy, so can choose an l₂ whose BFF is l₁ and sit it next to l₁. And we can continue this process. We can build a chain of kids to l's left following the edges of the graph in reverse, and similarly, we can build a chain of kids on r's right. When we are done, having added zero or more kids to each side, we have a line of kids from the same component that are all happy, so we can continue to add kids from other components right next to them!

To summarize the previous paragraph, we can build a chain of kids from each component with a cycle of length 2 (we already showed that cycles longer than that do not allow chains to be added). Since we want to construct the largest possible chain, we take the longest chain from each component with a cycle of length 2, and put them all together. That is, we sum their lengths as a possible final result to be compared with the largest cycle from the first case.

The following image illustrates the previous paragraph. On the left, a graph with three separate connected components is displayed. Red nodes are nodes in the cycles of each component. From the component with a cycle of length 4, we can build a circle (which we've shown on the right side of the image) but not add anything else. However, we can build a chain from each component with a cycle of length 2. Marked in green and orange are optimal choices for a chain on each side, and on the right you can see the circle of kids with the arrows indicating their BFFs at their side. You can see here how the cycles of length 2 allow us to add more kids, even including different connected components of the graph in the same circle, whereas longer cycles don't leave room for anyone else.

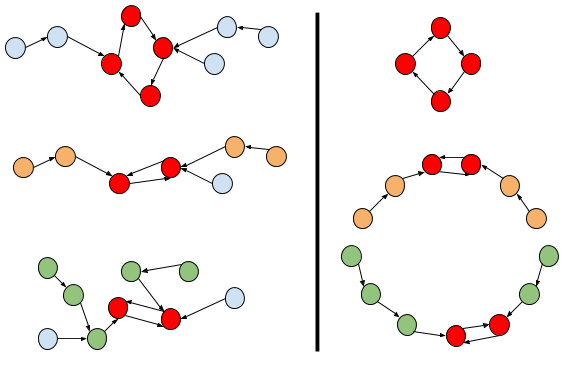
It is easy to find the connected components and their cycles using DFS or a number of other ways that we leave up to the reader to find and choose. There are also a number of ways to find the longest chains on each side of each cycle of length 2, that we also leave up to the reader. Notice that the process on each side is really similar to finding the height of a tree.