Google Code Jam Archive — Qualification Round 2016 problems
Overview
This year, we had 58,520 registrants, 27,170 contestants with at least one solved dataset on the scoreboard, and 1,710 contestants with perfect scores! We had a full 27 hours of coding fun, with the first correct submission at 2 minutes and 15 seconds. For the fourth year in a row, xiaowuc1 had the first correct submission of the Qualification Round! xiaowuc1 was also the third to a perfect score (49:13), behind Lewin in first place (40:51) and Endagorion in second place (47:47).
The first problem, Counting Sheep, was a relatively simple "try it and see" implementation exercise. Revenge of the Pancakes playfully alluded to Infinite House of Pancakes, a harder pancake-related problem from last year's Qualification round, but admitted a much simpler solution. Coin Jam was an unusual exercise in "mining" for "coins" with certain properties... or easily constructing them outright, if you found the right math trick! Finally, Fractiles was a more complex problem about logic and information.
Congratulations to our 22,154 competitors who earned at least 30 points and advanced to the Round 1 contests; we'll see you soon in Round 1A!
Cast
Problem A (Counting Sheep): Written and prepared by Ian Tullis.
Problem B (Revenge of the Pancakes): Written and prepared by Ian Tullis.
Problem C (Coin Jam): Written and prepared by Ian Tullis.
Problem D (Fractiles): Written by Pablo Heiber and Ian Tullis. Prepared by Jackson Gatenby and Pablo Heiber.
Solutions and other problem preparation and review by David Arthur, Minh Doan, Sumudu Fernando, Jackson Gatenby, Taman (Muhammed) Islam, Sean Lip, Igor Naverniouk, Karol Pokorski, Steve Thomas, Yerzhan Utkelbayev, and Jonathan Wills.
Analysis authors:
- Counting Sheep: Ian Tullis
- Revenge of the Pancakes: Timothy Loh and Pablo Heiber
- Coin Jam: Timothy Loh
- Fractiles: Pablo Heiber
A. Counting Sheep
Problem
Bleatrix Trotter the sheep has devised a strategy that helps her fall asleep faster. First, she picks a number N. Then she starts naming N, 2 × N, 3 × N, and so on. Whenever she names a number, she thinks about all of the digits in that number. She keeps track of which digits (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) she has seen at least once so far as part of any number she has named. Once she has seen each of the ten digits at least once, she will fall asleep.
Bleatrix must start with N and must always name (i + 1) × N directly after i × N. For example, suppose that Bleatrix picks N = 1692. She would count as follows:
- N = 1692. Now she has seen the digits 1, 2, 6, and 9.
- 2N = 3384. Now she has seen the digits 1, 2, 3, 4, 6, 8, and 9.
- 3N = 5076. Now she has seen all ten digits, and falls asleep.
What is the last number that she will name before falling asleep? If she will
count forever, print INSOMNIA instead.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each consists of one line with a single integer N, the number Bleatrix has chosen.
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1) and y is
the last number that Bleatrix will name before falling asleep, according to
the rules described in the statement.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1 GB.
1 ≤ T ≤ 100.
Small dataset (Test Set 1 - Visible)
0 ≤ N ≤ 200.
Large dataset (Test Set 2 - Hidden)
0 ≤ N ≤ 106.
Sample
5 0 1 2 11 1692
Case #1: INSOMNIA Case #2: 10 Case #3: 90 Case #4: 110 Case #5: 5076
In Case #1, since 2 × 0 = 0, 3 × 0 = 0, and so on, Bleatrix will never see any digit other than 0, and so she will count forever and never fall asleep. Poor sheep!
In Case #2, Bleatrix will name 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. The 0 will be the last digit needed, and so she will fall asleep after 10.
In Case #3, Bleatrix will name 2, 4, 6... and so on. She will not see the digit 9 in any number until 90, at which point she will fall asleep. By that point, she will have already seen the digits 0, 1, 2, 3, 4, 5, 6, 7, and 8, which will have appeared for the first time in the numbers 10, 10, 2, 30, 4, 50, 6, 70, and 8, respectively.
In Case #4, Bleatrix will name 11, 22, 33, 44, 55, 66, 77, 88, 99, 110 and then fall asleep.
Case #5 is the one described in the problem statement. Note that it would only show up in the Large dataset, and not in the Small dataset.
B. Revenge of the Pancakes
Problem
The Infinite House of Pancakes has just introduced a new kind of pancake! It has a happy face made of chocolate chips on one side (the "happy side"), and nothing on the other side (the "blank side").
You are the head waiter on duty, and the kitchen has just given you a stack of pancakes to serve to a customer. Like any good pancake server, you have X-ray pancake vision, and you can see whether each pancake in the stack has the happy side up or the blank side up. You think the customer will be happiest if every pancake is happy side up when you serve them.
You know the following maneuver: carefully lift up some number of pancakes (possibly all of them) from the top of the stack, flip that entire group over, and then put the group back down on top of any pancakes that you did not lift up. When flipping a group of pancakes, you flip the entire group in one motion; you do not individually flip each pancake. Formally: if we number the pancakes 1, 2, ..., N from top to bottom, you choose the top i pancakes to flip. Then, after the flip, the stack is i, i-1, ..., 2, 1, i+1, i+2, ..., N. Pancakes 1, 2, ..., i now have the opposite side up, whereas pancakes i+1, i+2, ..., N have the same side up that they had up before.
For example, let's denote the happy side as + and the blank side
as -. Suppose that the stack, starting from the top, is
--+-. One valid way to execute the maneuver would be to pick up
the top three, flip the entire group, and put them back down on the remaining
fourth pancake (which would stay where it is and remain unchanged). The new
state of the stack would then be -++-. The other valid ways would
be to pick up and flip the top one, the top two, or all four. It would not be
valid to choose and flip the middle two or the bottom one, for example; you can
only take some number off the top.
You will not serve the customer until every pancake is happy side up, but you don't want the pancakes to get cold, so you have to act fast! What is the smallest number of times you will need to execute the maneuver to get all the pancakes happy side up, if you make optimal choices?
Input
The first line of the input gives the number of test cases, T. T
test cases follow. Each consists of one line with a string S, each
character of which is either + (which represents a pancake that is
initially happy side up) or - (which represents a pancake that is
initially blank side up). The string, when read left to right, represents the
stack when viewed from top to bottom.
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1) and y is
the minimum number of times you will need to execute the maneuver to get all
the pancakes happy side up.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1 GB.
1 ≤ T ≤ 100.
Every character in S is either + or -.
Small dataset (Test Set 1 - Visible)
1 ≤ length of S ≤ 10.
Large dataset (Test Set 2 - Hidden)
1 ≤ length of S ≤ 100.
Sample
5 - -+ +- +++ --+-
Case #1: 1 Case #2: 1 Case #3: 2 Case #4: 0 Case #5: 3
In Case #1, you only need to execute the maneuver once, flipping the first (and only) pancake.
In Case #2, you only need to execute the maneuver once, flipping only the first pancake.
In Case #3, you must execute the maneuver twice. One optimal solution is to
flip only the first pancake, changing the stack to --, and then
flip both pancakes, changing the stack to ++. Notice that you
cannot just flip the bottom pancake individually to get a one-move solution;
every time you execute the maneuver, you must select a stack starting from the
top.
In Case #4, all of the pancakes are already happy side up, so there is no need to do anything.
In Case #5, one valid solution is to first flip the entire stack of pancakes to
get +-++, then flip the top pancake to get --++, then
finally flip the top two pancakes to get ++++.
C. Coin Jam
Problem
A jamcoin is a string of N ≥ 2 digits with the following properties:
- Every digit is either
0or1. - The first digit is
1and the last digit is1. - If you interpret the string in any base between 2 and 10, inclusive, the resulting number is not prime.
Not every string of 0s and 1s is a jamcoin. For
example, 101 is not a jamcoin; its interpretation in base 2 is 5,
which is prime. But the string 1001 is a jamcoin: in bases 2
through 10, its interpretation is 9, 28, 65, 126, 217, 344, 513, 730, and 1001,
respectively, and none of those is prime.
We hear that there may be communities that use jamcoins as a form of currency. When sending someone a jamcoin, it is polite to prove that the jamcoin is legitimate by including a nontrivial divisor of that jamcoin's interpretation in each base from 2 to 10. (A nontrivial divisor for a positive integer K is some positive integer other than 1 or K that evenly divides K.) For convenience, these divisors must be expressed in base 10.
For example, for the jamcoin 1001 mentioned above, a possible set
of nontrivial divisors for the base 2 through 10 interpretations of the jamcoin
would be: 3, 7, 5, 6, 31, 8, 27, 5, and 77, respectively.
Can you produce J different jamcoins of length N, along with proof that they are legitimate?
Input
The first line of the input gives the number of test cases, T. T test cases follow; each consists of one line with two integers N and J.
Output
For each test case, output J+1 lines. The first line must consist of
only Case #x:, where x is the test case number
(starting from 1). Each of the last J lines must consist of a jamcoin of
length N followed by nine integers. The i-th of those nine integers
(counting starting from 1) must be a nontrivial divisor of the jamcoin when
the jamcoin is interpreted in base i+1.
All of these jamcoins must be different. You cannot submit the same jamcoin in two different lines, even if you use a different set of divisors each time.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1 GB.
T = 1. (There will be only one test case.)
It is guaranteed that at least J distinct jamcoins of length N
exist.
Small dataset (Test Set 1 - Visible)
N = 16.
J = 50.
Large dataset (Test Set 2 - Hidden)
N = 32.
J = 500.
Note that, unusually for a Code Jam problem, you already know the exact contents of each input file. For example, the Small dataset's input file will always be exactly these two lines:
1
16 50
So, you can consider doing some computation before actually downloading an input file and starting the clock.
Sample
1 6 3
Case #1: 100011 5 13 147 31 43 1121 73 77 629 111111 21 26 105 1302 217 1032 513 13286 10101 111001 3 88 5 1938 7 208 3 20 11
In this sample case, we have used very small values of N and J for ease of explanation. Note that this sample case would not appear in either the Small or Large datasets.
This is only one of multiple valid solutions. Other sets of jamcoins could have been used, and there are many other possible sets of nontrivial base 10 divisors. Some notes:
-
110111could not have been included in the output because, for example, it is 337 if interpreted in base 3 (1*243 + 1*81 + 0*27 + 1*9 + 1*3 + 1*1), and 337 is prime. -
010101could not have been included in the output even though10101is a jamcoin, because jamcoins begin with1. -
101010could not have been included in the output, because jamcoins end with1. -
110011is another jamcoin that could have also been used in the output, but could not have been added to the end of this output, since the output must contain exactly J examples. -
For the first jamcoin in the sample output, the first number after
100011could not have been either 1 or 35, because those are trivial divisors of 35 (100011in base 2).
D. Fractiles
Problem
Long ago, the Fractal civilization created artwork consisting of linear
rows of tiles. They had two types of tile that they could use: gold
(G) and lead (L).
Each piece of Fractal artwork is based on two parameters: an original sequence of K tiles, and a complexity C. For a given original sequence, the artwork with complexity 1 is just that original sequence, and the artwork with complexity X+1 consists of the artwork with complexity X, transformed as follows:
- replace each
Ltile in the complexity X artwork with another copy of the original sequence - replace each
Gtile in the complexity X artwork with KGtiles
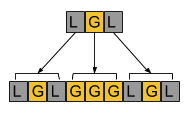
For example, for an original sequence of LGL, the pieces of
artwork with complexity 1 through 3 are:
- C = 1:
LGL(which is just the original sequence) - C = 2:
LGLGGGLGL - C = 3:
LGLGGGLGLGGGGGGGGGLGLGGGLGL
Here's an illustration of how the artwork with complexity 2 is generated from the artwork with complexity 1:
You have just discovered a piece of Fractal artwork, but the tiles are too
dirty for you to tell what they are made of. Because you are an expert
archaeologist familiar with the local Fractal culture, you know the values of
K and C for the artwork, but you do not know the original
sequence. Since gold is exciting, you would like to know whether there is at
least one G tile in the artwork. Your budget allows you to hire
S graduate students, each of whom can clean one tile of your choice (out
of the KC tiles in the artwork) to see whether the
tile is G or L.
Is it possible for you to choose a set of no more than S specific tiles
to clean, such that no matter what the original pattern was, you will be
able to know for sure whether at least one G tile is present in
the artwork? If so, which tiles should you clean?
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each consists of one line with three integers: K, C, and S.
Output
For each test case, output one line containing Case #x: y, where
x is the test case number (starting from 1) and y is
either IMPOSSIBLE if no set of tiles will answer your question, or
a list of between 1 and S positive integers, which are the positions of
the tiles that will answer your question. The tile positions are numbered from
1 for the leftmost tile to KC for the rightmost tile.
Your chosen positions may be in any order, but they must all be different.
If there are multiple valid sets of tiles, you may output any of them. Remember that once you submit a Small and it is accepted, you will not be able to download and submit another Small input. See the FAQ for a more thorough explanation. This reminder won't appear in problems in later rounds.
Limits
Time limit: 20 seconds per test set.
Memory limit: 1 GB.
1 ≤ T ≤ 100.
1 ≤ K ≤ 100.
1 ≤ C ≤ 100.
KC ≤ 1018.
Small dataset (Test Set 1 - Visible)
S = K.
Large dataset (Test Set 2 - Hidden)
1 ≤ S ≤ K.
Sample
5 2 3 2 1 1 1 2 1 1 2 1 2 3 2 3
Case #1: 2 Case #2: 1 Case #3: IMPOSSIBLE Case #4: 1 2 Case #5: 2 6
Note: for some of these sample cases, other valid solutions exist.
In sample case #1, there are four possible original sequences: GG,
GL, LG, and LL. They would produce the
following artwork, respectively:
- Original sequence
GG:GGGGGGGG - Original sequence
GL:GGGGGGGL - Original sequence
LG:LGGGGGGG - Original sequence
LL:LLLLLLLL
One valid solution is to just look at tile #2. If tile #2 turns out to be
G, then you will know for sure the artwork contains at least one
G. (You will not know whether the original sequence is
GG, GL, or LG, but that doesn't matter.)
If tile #2 turns out to be L, then you will know that the original
sequence must be LL, so there are no Gs in the
artwork. So 2 is a valid solution.
On the other hand, it would not be valid to just look at tile #1. If it turns
out to be L, you will only know that the original sequence could
have been either LG or LL. If the original sequence
is LG, there is at least one G in the artwork, but if
the original sequence is LL, there are no Gs. So
1 would not be a valid solution.
Note that 1 2 is also a valid solution, because tile #2 already
provides all the information you need. 1 2 3 is not a valid
solution, because it uses too many tiles.
In sample case #2, the artwork must consist of only one tile: either
G or L. Looking at that tile will trivially tell you
whether or not the artwork has a G in it.
In sample case #3, which would not appear in the Small dataset, the artwork
must be either GG, GL, LG, or
LL. You can only look at one tile, and neither of them on its own
is enough to answer the question. If you see L for tile #1, you
will not know whether the artwork is LG or LL, so you
will not know whether any Gs are present. If you see
L for tile #2, you will not know whether the artwork is
GL or LL, so you will not know whether any
Gs are present.
Sample case #4 is like sample case #3, but with access to one more tile. Now you can just look at the entire artwork.
In sample case #5, there are eight possible original sequences, and they would produce the following artwork:
- Original sequence
GGG:GGGGGGGGG - Original sequence
GGL:GGGGGGGGL - Original sequence
GLG:GGGGLGGGG - Original sequence
GLL:GGGGLLGLL - Original sequence
LGG:LGGGGGGGG - Original sequence
LGL:LGLGGGLGL - Original sequence
LLG:LLGLLGGGG - Original sequence
LLL:LLLLLLLLL
One valid solution is to look at tiles #2 and #6. If they both turn out to
be Ls, the artwork must be all Ls. Otherwise, there
must at least one G. Note that 1 2 would not be a
valid solution, because even if those tiles both turn out to be Ls,
that does not rule out an original sequence of LLG.
6 2 would be a valid solution, since the order of the positions
in your solution does not matter.
Analysis — A. Counting Sheep
The most natural approach to this problem is to simulate the process: keep track of which digits Bleatrix has seen so far, and then keep generating and checking the numbers she names until she has seen all of the digits 0-9. But are there other cases like N = 0 that go on forever or take an unacceptably long time?
One way to answer this question for the purposes of the problem to just check all possible cases between 0 and 106 before downloading the Large dataset. With a well-written program on a reasonably fast machine, this should take only a few seconds.
More generally, it can be proven that for any N > 0, the sheep doesn't have to keep naming numbers for very long:
- Regarding the digit 0: The tenth number that Bleatrix names is 10 times N, and is therefore guaranteed to end in 0.
- Regarding digits 1-9: Consider the smallest power of 10 greater than N; call it P. Once the process reaches a number at least as large as P, then the leftmost digit will take on every possible value from 1-9 as the number increases up to (or past) 9P. No digit can be skipped, because that would require the step between successive numbers (which equals N) to be larger than P... but we know that N is less than P because of how we chose P.
Since, by definition of P, 10N ≥ P, we will reach a number larger than P after naming at most 10 numbers, and we will reach a number greater than 9P after naming at most 90 numbers. So, after checking for the special case of N = 0, we can run our simulation without fear of running forever, running for long enough to run out of time, or overflowing even a 32-bit integer. Within the limits of the Small and Large datasets, the worst cases turn out to be 125 followed by any number of zeroes. In those cases, Bleatrix will name 72 numbers before falling asleep.
Analysis — B. Revenge of the Pancakes
In the small case we have a stack of at most 10 pancakes. The total number of possible different states we can get by performing any number of flips is thus 210 = 1024. As this is a small number of states, we can solve the small test case by performing a breadth first search over this state space. For N pancakes, this can be implemented to complete within O(N 2N) time.
The large case requires a much more efficient solution. Imagine a large stack of pancakes, starting with a few happy side up, then a few blank side up, a few more happy side up, and so on. Intuitively it seems like a good idea to avoid flipping between two pancakes facing the same direction and instead try and make larger groups of pancakes facing the same direction. Define the "grouped height" of a prefix of the stack of pancakes (possibly the entire stack) to be the number of groups of contiguous pancakes facing the same direction. The goal state has a grouped height of 1. We can consider how various flips affect the grouped height of a stack of pancakes:
- If we flip a group of pancakes that has an even grouped height, then the stack's grouped height will be unchanged.
- If we flip a group of pancakes that has an odd grouped height, then the
stack's grouped height will
- increase by 1 if we flip between two pancakes facing the same direction.
- decrease by 1 if we flip between two pancakes facing opposite directions.
- be unchanged if we flip the entire stack.
Since the above statements categorize all possible flips, a flip can reduce the grouped height of a stack by at most 1. As the goal state has a grouped height of 1, a stack with grouped height of H requires at least H-1 flips to reach the goal state. Considering simple cases, for example those in the sample input, we can see that H-1 flips is not necessarily sufficient. A stack consisting only of blank side up pancakes has H = 1 but we need to flip the entire stack to make the pancakes happy side up. Given a stack where the bottom pancake is blank side up, we need to flip the entire stack at least once as the bottom pancake is only flipped when we flip the entire stack. Flipping the entire stack does not affect the grouped height of a stack so this gives us a stricter lower bound of either H-1 flips if the bottom pancake is happy side up or H flips if the bottom pancake is blank side up.
For a stack with H > 1, we can always flip the topmost group of pancakes facing the same direction to decrease the grouped height by 1. Thus the stricter lower bound is a sufficient number of flips as the following greedy strategy takes exactly that many moves: repeatedly flip the topmost group of pancakes facing in the same direction (reducing the grouped height by 1 each flip) until the grouped height is 1 and then flip the entire stack once if needed.
The problem only asks for the minimum number of flips and not which flips to
make. As argued above, this is 1 less than the grouped height if the bottom
pancake is happy side up and exactly the grouped height if the bottom pancake
is blank side up. A sample implementation in Python is provided below, using
the fact that the grouped height is one more than the number of times the
string changes from + to - or vice versa.
def minimumFlips(pancakes):
groupedHeight = 1 + pancakes.count('-+') + pancakes.count('+-')
if pancakes.endswith('-'):
return groupedHeight
else:
return groupedHeight - 1
Analysis — C. Coin Jam
One approach here is to enumerate strings of length N and see if they are jamcoins. To iterate over potential jamcoins, we can iterate over the base-2 interpretations (odd numbers between 2N-1+1 and 2N-1, inclusive) and use a recursive method to convert these to different bases.
For the Small dataset, it is sufficient to use trial division to find factors of potential jamcoins. Concretely, we can look for a nontrivial divisor of an integer k by testing divisibility of every integer in increasing order from 2 to the square root of k, inclusive and stopping if we find one. Searching past the square root of the number is not needed as if k has some nontrivial divisor d, then k / d is also a non-trivial divisor and the smaller of d and k / d is at most the square root of k. A sample implementation of this in C++ looks like this:
long long convertBinaryToBase(int x, int base) {
// Some languages have built-ins which make this easy.
// For example, in Python, we can avoid recursion and
// just return int(bin(x)[2:], base)
if (x == 0)
return 0;
return base * convertBinaryToBase(x / 2, base) + (x % 2);
}
long long findFactor(long long k) {
for (long long d = 2; d * d <= k; d++)
if (k % d == 0)
return d;
return 0;
}
void printCoins(int N, int X) {
for (long long i = (1 << N-1) + 1; X > 0; i += 2) {
vector<long long> factors;
for (int base = 2; base <= 10; base++) {
long long x = convertBinaryToBase(i, base);
long long factor = findFactor(x);
if (!factor)
break;
factors.push_back(factor);
}
if (factors.size() < 9)
continue;
cout << convertBinaryToBase(i, 10);
for (long long factor : factors)
cout << " " << factor;
cout << endl;
X -= 1;
}
}
Solving the large test case may present unique challenges, depending on the programming language used. We're given that N = 32, which means that in base 10 we'll have 32-digit numbers, which we can't store in a 64-bit integer. These numbers are also large enough that running the trial division algorithm on a single prime would take a huge amount of time, potentially longer than the duration of this contest! While we can solve these issues by stopping the trial division early (say, after checking up to 1000) and using arbitrary precision integers, there's actually a much nicer approach!
We can make some observations about jamcoins if we look at the output to the Small dataset from our program above. Considering the first 50 jamcoins of length 16, we find that 18 of them have divisors "3 2 3 2 7 2 3 2 3" and 11 of them have divisors "3 2 5 2 7 2 3 2 11". What's the pattern in these numbers? The numbers 5, 7, 11 from the second list provide a useful hint: they're one more than their respective bases. Giving this some thought, we can notice that the second list of divisors is formed by taking the smallest prime factor of b+1 for each base b. This suggests that b+1 is always a divisor for each of these 11 jamcoins, and we can easily verify that this is true. Understanding the other common divisor list is left as an exercise for the reader.
Note that b+1 in base b is 11b. A simple test
exists to determine divisibility of 11 in base-10: a number is divisible by 11
if the sum of its digits in odd positions and the sum of its digits in even
positions differ by a multiple of 11. This
divisibility rule
for 11 can be extended to a simple rule: a string of 0s and
1s which starts and ends with a 1 and has the same
number of 1s at odd and even indices is divisible by b+1 when
interpreted as a base-b number. Such a string is therefore a jamcoin,
but not every jamcoin necessarily matches this condition. A stricter condition
that may be easier to notice is that a string of 0s and
1s which starts and ends with a 1 is a jamcoin if all
1s are paired, i.e. it matches the regular expression
11(0|11)*11. For example, in any base b,
11011b = 1001b × 11b.
The last example here also suggests a more general rule. Consider any string
p of 0s and 1s with at least two
characters, which starts and ends with a 1. Any string which is
p repeated multiple times with any number of 0s
between repetitions is a jamcoin. In the previous example we have
p = 11 and this general rule can be expressed as the
regular expression (1[01]*1)(0*\1)+. For example, in any base b,
1110100011101011101b =
11101b × 100000001000001b.
We can use any of these rules to mine jamcoins easily. The Python 2 code below
mines jamcoins with exactly 5 pairs of 11s, which finds enough for
both the Small and Large datasets.
def printCoins(N, X):
# N digits, 10 1s, N-10 0s
for i in range(N-10):
for j in range(N-10-i):
for k in range(N-10-i-j):
l = N-10-i-j-k
assert l >= 0
template = "11{}11{}11{}11{}11"
output = template.format("0"*i, "0"*j, "0"*k, "0"*l)
factors = "3 2 5 2 7 2 3 2 11"
print output, factors
X -= 1
if X == 0:
return
# If we get here, we didn't mine enough jamcoins!
assert False
Analysis — D. Fractiles
This problem is more about analyzing an existing algorithm than writing a new one. Once you understand how more complex artwork depends on the original sequence, you can solve the problem with a short piece of code.
The first thing to notice is that if the original sequence is all Ls, the artwork will
be all Ls, no matter what the value of C is. If we choose some set of tiles
that all turn out to be Ls for some original sequence other than all Ls,
then our solution is invalid, because we won't be able to tell whether the artwork was based on
that original sequence or on an original sequence of all Ls. This means we have to
come up with a set of positions to check out such that for any original sequence besides all
Ls, we will see at least one G.
Small dataset
In the Small dataset, since we can check as many tiles as the length of the original sequence, we may be tempted to try to reconstruct it in full. And while this is possible (we'll get there in a moment), there is an easier alternative. The simplest solution, as it turns out, is to always output the integers 1 through K. It can be easily proved that it works with the following two-case analysis. Let us call the original sequence O, and let Ai be the artwork of complexity i for a fixed O.
1. Suppose that O starts with an L. Let us prove that each
Ai starts with O. This is trivially true for
A1 = O. Now, if Ai starts with O, it also
starts with an L, and since the transformation maps that first L into a
copy of O, Ai+1 starts with O. By induction, each
Ai starts with O. Then, by checking positions 1 through K,
we are checking a copy of the original sequence O, so if there are any Gs in
O, we will see a G.
2. Suppose instead that O starts with a G. Let us prove that each
Ai starts with a G. This is trivially true for
A1 = O. Now, if Ai starts with a G,
then Ai+1 also starts with a G, since the transformation maps
that G at the start of Ai to K Gs at the
start of Ai+1. By induction, each Ai starts with
G. Then, since we are checking position 1, we will see a G.
Since we will see at least one G for any original sequence that is not all
Ls, and only Ls for the original sequence that is all Ls,
we have answered the question successfully. Notice that this also proves that there is no
impossible case in the Small dataset.
The proofs above hint at another possible solution for the Small dataset that gets enough information from the tiles to know the entire O. We will explain it not only because it is interesting, but also because it is a stepping stone towards a solution for the Large dataset.
We have seen that position 1 of any Ai is always equal to position 1 of O. Is there any position in Ai that is always equal to position 2 of O? It turns out that there is, and the same is true for any position of O.
Consider position 2 of O as an example. It is position 2 in A1 = O. When A2 is produced from A1, the tile at position 2 of A1 determines which tiles will appear at positions K + 1 through K + K of A2. In particular, the second of those tiles, the tile at position K + 2 of A2, is the same as the tile at position 2 of A1. Then, it follows that position K + 2 of A2 generates positions K*(K + 2 - 1) + 1 through K*(K + 2) of A3, and the second of those tiles, at position K*(K + 2 - 1) + 2 of A3, is also a copy of position 2 of O. You can follow this further to discover which position of AC is equal to position 2, or you can write a program to do it for you. Similarly, for each position of O there is exactly one "fixed point" position in AC that is always equal in value, and you can get those with a program by generalizing the procedure described for position 2. If you check out all of those positions, you obtain a different result for every possible O, which makes the solution valid.
Large dataset
The reasoning that we just used to find fixed points will help us solve the Large. Each position
in Ai generates K positions in Ai+1. So,
indirectly, each position in Ai also generates K2
positions in Ai+2, K3 positions in
Ai+3, and so on. Let us say that a position in
Ai+d is a descendant of a position p in
Ai if it was generated from a position in
Ai+d-1 generated from a position in
Ai+d-2 ... generated from position p in
Ai. Notice that a G in any given position of any
Ai implies a G in all descendant positions. However, if there
is an L in position p of Ai, a descendant position
(p - 1)*K+d (with 1 ≤ d ≤ K) of
Ai+1 will be equal to position d of O. So, position
(p - 1)*K+d of Ai+1 is an L if and only
if both position p of Ai and position d of O are
Ls. If we take this further, we arrive at a key insight: any position of any
Ai is an L if and only if a particular set of positions in
O are Ls.
We can find those positions by thinking about the orders in which the descendants at each level
were produced. For instance, for K=3, position 8 of A3 is descendant
number 2 of position 3 of A2, which in turn is descendant number 3 of position
1 of A1. That means that position 8 of A3 is L
if and only if positions 2, 3 and 1 of O are all Ls. So, just by looking at
position 8 of A3, we know whether the original sequence had a
G in at least one of those three positions.
Generalizing this, if we start at position p1 of A1 = O,
and take its p2-th descendant in A2, and then take its
p3-th descendant in A3, and so on, until taking the
pC-th descendant in AC, we have a single position
that tells us whether the original sequence has a G in positions
p1, p2, ..., pC. And, conversely, for
any position in AC, we can find a corresponding sequence of C
positions that lead to it. So, each position we check on AC can cover up
to C positions of O, and will cover exactly C positions if we make the right
choice. Since we need to cover all K positions of the original sequence, that means the
impossible cases are exactly those where S*C < K — that is, where
getting C positions out of every one of our S tile choices is still not enough.
For the rest, we can assign a list of positions [1, 2, ..., C] to tile choice 1,
[C+1, C+2, 2C] to tile choice 2, and so on until we get to K. If the
last tile choice has a list shorter than C, we can fill it up with copies of any integer
between 1 and K. Now all we need to do is match each of these lists to a position in
AC, which we can do by following the descendant path (descendants of
position p are always positions (p - 1)*K+1 through
(p - 1)*K+K). This simple Python code represents this idea:
def Solve(k, c, s):
if c*s > k:
return [] # returns an empty list for impossible cases
tiles = []
# the list for the last tile choice is filled with copies of k
# i is the first value of the list of the current tile choice
for i in xrange(1, k + 1, c):
p = 1
# j is the step in the current list [i, i+1, ..., i+C-1]
for j in xrange(c):
# the min fills the last tile choice's list with copies of k
p = (p - 1) * k + min(i + j, k)
tiles.append(p)
return tiles