Google Code Jam Archive — World Finals 2015 problems

Let us call the length of the input sequence N. There are N+1 possible "slots" in which the new element can end up — we number them from 0 to N, where 0 is the slot before the first element of a, and N is the slot after the last element of a.

At any point in our search, we will have narrowed down the possible location of the correct slot to an interval of possible slots. We then want to find out which slot in that interval is the correct one; we call this "solving" the interval.

For a given cost C and position X, we want to compute the largest possible interval of slots, beginning at X, which we can solve in cost C or less. Call the rightmost slot of that interval f(C,X). We will compute f using dynamic programming.

Clearly if C=0, then f(C,X)=X and the interval is empty. (Since each comparison costs at least 1, we cannot make any comparisons.)

Otherwise, assume we have an interval [X,Y], where X < Y, that we can solve at a cost no greater than C. The solution must involve an initial comparison at an index i, where i is in [X,Y-1], which costs a_i. Then we will have narrowed down the correct slot to either the interval of slots to the left of index i, which is [X,i]; or the interval of slots to the right of index i, which is [i+1,Y].

Each of these intervals must be solvable with a cost no greater than C-a_i, i.e., f(C-a_i, X) ≥ i, and f(C-a_i, i+1) ≥ Y.

We want to find the largest Y for which the above statements hold. To limit the number of possible choices for i and Y, we always use Y=f(C-a_i, i+1), since by definition this is the largest possible Y for a given choice of X and i. Also, instead of trying every value of i in [X, f(C-a_i, X)], we iterate through each possible value of a_i from 1 to 9, and try the largest index i in [X, f(C-a_i, X)] with that value. (Smaller indices i with the same value of a_i could not produce a larger Y). If there are no usable values of i (because C is too small, or X=N) then f(C,X)=X.

We compute f(C,X) in this way for increasing values of C, until we find the minimal C such that f(C,0)=N. This C is the answer.

The maximum value for the resulting C occurs when every array value is 9, in which case we can't do better than a standard binary search, which takes O(log N) comparisons of cost 9 each. That means computing f(C,X) over a domain of size 9 log N × N. Since the computation at each position takes constant time (we try 9 things), the overall algorithm takes O(N log N) time, with a somewhat large constant because of the two factors of 9 mentioned previously.

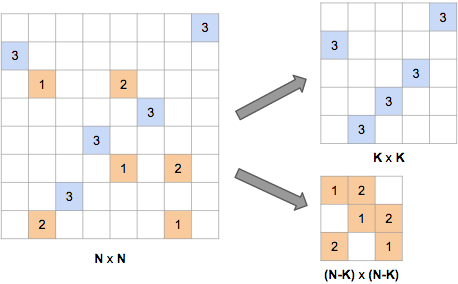
Let N be the size of the grid, and K be the number of 3-family tents. We can decompose the problem of counting the number of arrangements for given values of N and K by noting that we can first choose a set of K rows and K columns to contain the 3-family tents, and the remaining set of N-K rows and N-K columns will contain the 2-family and 1-family tents. (See the diagram above.) The number of arrangements is then the product of the following:

• The number of ways to choose the sets of rows and columns. There are C(N,K)^2 ways of choosing the K rows and columns, where C(N,K) is a binomial coefficient.
• The number of ways to assign the 3-family tents to (row, column) pairs. We can do this assignment by taking a permutation of the columns, and assigning the i^th column in the permutation to the i^th row in the set of K rows. There are K! such permutations.
• The number of ways to assign the 2-family tents to (row, column) pairs. Similarly to the 3-family tents, there are (N-K)! ways to do this.
• The number of ways to assign the 1-family tents to (row, column) pairs. Not all of the (N-K)! permutations of columns can be used, since we have the additional requirement that we can't use a (row, column) pair in which we've already placed a 2-family tent. To deal with this, we reformulate what we need to do here: for each row X in the set of N-K rows, we need to choose a unique row Y from the same set, find the column C such that there is a 2-family tent at (Y,C), and place a 1-family tent at (X,C). The space at row X, column C is guaranteed not to already have a tent. So we need a permutation of the N-K rows, with the additional requirement that no row is unchanged by the permutation – that is, for each row X, we choose a row different to X as the corresponding row Y in the permutation. Such a permutation is called a derangement. The number of derangements of size N-K is written !(N-K).

Now, the product of all these terms is:

C(N,K)^2 × K! × (N-K)! × !(N-K) = N!^2 / (K! × (N-K)!) × !(N-K).

We get the answer to the problem by summing this value (mod 10^9 + 7) for all values of K from X to N.

We can do that efficiently by precomputing K!, 1/K!, and !K mod 10^9 + 7 for all values of K up to N. Factorials can be computed with the obvious recurrence. 1/K! mod 10^9+7 can be computed from K! with the extended Euclidean algorithm or using Fermat's little theorem. !K can be computed with the recurrence:

!1 = 0, !2 = 1, !X=(X-1)(!(X-1)+!(X-2)).

A brute force O(N²) strategy will work for the Small dataset: for each position, compute the cumulative number of ones seen so far, and then check every possible pair of start and end points in the sequence. But N can be up to half a million in the Large dataset!

We will read the string from left to right and keep track of the number of ones O_i seen after reading the first i digits. We will examine each i between 0 and N, inclusive, so that we consider both the empty prefix and the full string. We will maintain an initially empty set of points, and for each i, we will add p_i = (i, F × i - O_i) to the set. Notice that the fraction of ones in the substring starting at position i+1 and ending at position j is (O_j - O_i) / (j - i), and the difference from F is F - (O_j - O_i) / (j - i) = (F(j - i) - O_j + O_i) / (j - i), which is the slope between p_i and p_j. Finding the p_i and p_j that minimize the absolute value of this slope is equivalent to solving the problem.

It is hard to see (but easy to prove) that the slope with minimal absolute value occurs between two points that are consecutive in sorted order by y coordinate: if there is a point r that has a y coordinate between the y coordinates of two other points p and q, the slope between p and q (call it s) is the weighted average of the slope between p and r and the slope between q and r; either those two slopes are equal to s, or one of them must be less than s. A more visual way to see this is to draw the segment p-q and place r on it. That makes all three slopes equal. Moving r horizontally clearly makes the slope of one of the segments pr and qr increase and the slope of the other one decrease.

This insight saves us from checking all pairs of points, and reduces the time complexity of the problem to O(N log N), which is imposed by the single sorting operation.

Let G be the graph, s be the entrance node, and t be the node with the secret weapon.

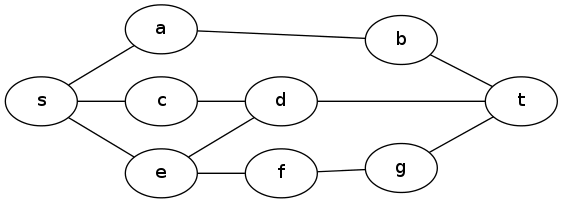
For the small input, we start by finding the shortest distance through the graph from s to t using, e.g., Dijkstra’s algorithm. Call this distance L. If K=0, we cannot obstruct anything, so the answer is simply L.

Now assume K > 0. It is always advantageous to obstruct s, so let’s begin by doing this: reduce K by one, and increase L by 1. Next we want to find if we can increase L one more by obstructing other nodes. This means that every shortest path from s to t must have another obstructed node in it (other than s). We can turn this into a standard graph problem in the following way -- take the subgraph of G which contains all the edges and nodes in a shortest path from s to t. Make each edge directed, pointing in the direction of the path it belongs to.

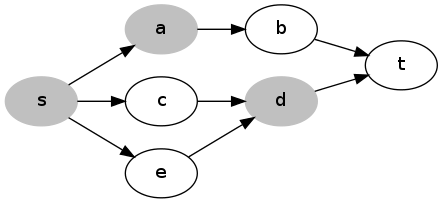
Now, if there is a set of up to K nodes we can obstruct that covers all the paths, for example a and d in the diagram above, then removing those nodes cuts the graph, separating s and t. So we need to solve the minimum vertex cut problem on this graph and check if the cut has size at most K. To do this, we convert it to an edge cut problem by changing the graph so that each vertex except s and t is split into two nodes, with an edge of capacity 1 between them. The original edges are converted to infinite-capacity edges, as in the diagram below:

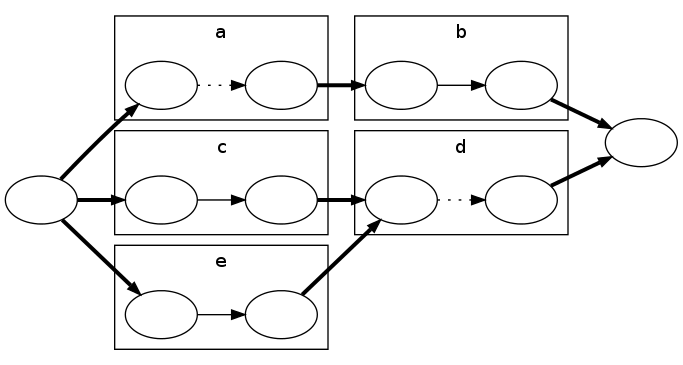
A vertex cut of K vertices in the earlier graph will correspond to an edge cut of capacity K in this new graph. In the example above, cutting the edges between the pairs of nodes for a and d cuts the graph. Now we have a minimum edge cut problem, and we can apply the max flow / min cut theorem — the size of the minimum edge cut is the size of the maximum flow — and use one of the standard algorithms for finding the maximum flow. If there exists a flow that is larger than K, then the answer is L, otherwise the answer is L+1.

Now for the large input. We will check, for successive values of X starting at 1, whether it is possible to obstruct up to K nodes in order to stop the guards traveling from node s to node t in time ≤ X. We call this proposition P(X). The first value of X where P(X) is false is the answer.

To determine the truth of P(X) for a specific X, we construct a new graph G', which has a node for each triplet (v, x, b) where v is a vertex in G, x is an integer between 0 and X, and b is true or false. Node (v, x, b) represents that the guards can reach node v in time x if b is false, or reach node v and surpass the obstruction in time x, if b is true. We add the following edges:

1. (v, x, false) to (v, x, true), for each v and x. (This means a free pass through an obstruction; removing one of these is equivalent to not adding an obstruction at v, if you remove the one for the appropriate x.)
2. (v, x, false) to (v, x+1, true), for each v and x < X-1. (a non-free pass through an obstruction) (v, x, false) to (v, x+1, false), for each v and x < X; (Stay put for 1 time unit.)
3. (v, x, true) to (w, x+1, false), for each x < X and each edge vw in G. (Transverse an edge in 1 time unit).

Let σ be the node (s, 0, false), and τ be the node (t, X, false). Assuming no nodes are obstructed, we can see that the following properties hold for G':

• There is a path from σ to (v, x, false) if and only if the guards can arrive at node v at a time ≤x.
• There is a path from σ to (v, x, true) if and only if the guards can leave node v at a time ≤x.
• There is a path from σ to τ if and only if it is possible for the guards to travel from s to t in G in time ≤ X.

If some nodes in G are obstructed, the properties above still hold if we delete all the edges in set 1 of the four sets above, where the corresponding v is one of the obstructed nodes. So P(X) is equivalent to a graph cut problem -- determining whether we can disconnect σ and τ by cutting the set 1 edges for up to K nodes of G.

In G, after we choose the nodes to obstruct, for each node v, all of the optimal paths from s to t that pass through v do so at the same time, so the ability to obstruct v was only "useful" at a given time time. So if our ability to obstruct a node were changed to an ability to obstruct a node at just one particular time, the result would be no different. Similarly, in G', after removing a set of edges, for each v, there will only be at most one x for which it was "useful" to cut the edge from (v, x, false) to (v, x, true).

We can prove this more formally: let A be a set of edges from set 1 that have been removed to disconnect σ and τ, and say that it contains the edges from (v, x₀, false) to (v, x₀, true) and from (v, x₁, false) to (v, x₁, true) for some v and x0 < x₁. If both edges are necessary, then there must be paths from σ to (v, x₀, false) and (v, x₁, false), and paths from (v, x₀, true) and (v, x₁, true) to τ. But now there is a path from σ to τ via (v, t₀, false), (v, t₁-1, false), and (v, t₁, true), so σ and τ are not disconnected at all! So for any set of edges A which disconnect σ and τ, there is a subset of A which disconnects σ and τ and has at most one edge cut for any node in G.

This means that P(X) is equivalent to being able to disconnect σ and τ by cutting up to K edges from set 1. As with the small input, this is equivalent to a max flow problem, with unit capacity on the set 1 edges and infinite capacity on the others.

We can solve all these flow problems quite quickly, since we do not need to recompute the maximum flow from scratch each time we increase X — we just add one more "layer" of nodes and edges for the new X value, and update the flow.

Every spell in the spell-testing procedure can be interpreted as an M-dimensional vector, and the current state of Edythe’s inventory is also an M-dimensional vector (initially an all-zero vector). Casting a spell is equivalent to adding the vector describing the spell to the vector describing Edythe’s inventory, and then changing all the negative values in Edythe’s inventory to zero (this corresponds to retrieving the exact necessary amount from Merlin’s storehouse). Edythe is aiming to maximize the sum of all the coordinates at the end.

Note that even if we allowed Edythe to zero a coordinate of the vector describing her inventory at any time, it would never be advantageous to zero it when it is positive, and it would never be disadvantageous to zero it when it is negative - so the final answer will not change if we give Edythe full freedom over when and which coordinates of her inventory get zeroed. We will solve this less constrained problem from now on.

Notice that it never makes sense to zero a given coordinate more than once, since the last zeroing will make the previous ones irrelevant anyway. So from now on, we will solve an equivalent problem — given a list of spells, and the opportunity to zero each coordinate of the accumulated sum exactly once, at any point of the summation, maximize the final sum of all the coordinates. Thus, a solution candidate can be equivalently described as a permutation of the N spells, plus the moments in time at which we zero each coordinate.

Let’s fix the order in which coordinates get zeroed (we will later iterate over all M! possible orderings), and look at one particular spell. We will try to figure out the best time to cast it. If we cast it before any coordinate is zeroed, then the result will be the same as if we had not cast it at all — every coordinate will eventually be reset to zero after casting the spell anyway. Now assume we cast it when k coordinates have already been zeroed, and the others have not. Compared to the situation when we don’t cast it at all, the end result is that the values of the spell on the k already-zeroed coordinates will be added to the final values of these coordinates, and so the sum of these values will be added to Edythe’s final result. So, for every spell, we check each of the M+1 possibilities for k, and choose the one which will give the largest contribution to the final result.

So a solution can work as follows: take every possible ordering P of the M dimensions. For each ordering P, iterate over all the spells, and for each spell find which of the M+1 values for k will cause the spell to contribute the most to the final result. The sum of all these contributions for all the spells is the best possible score for this ordering P; the maximum score over all orderings is the answer. The runtime is O((M+1)! N), which will easily run in time for N = 100 and M = 8.

In this problem, we are given a version of a small programming language, and we are required to track the number of operations executed as a program runs. The memory is a circular array of 2⁴⁰ positions, and all values are considered modulo 256 (for convenience, we shift values one position to make them go [0,255]). The program can run for a really long time, so our approach is to simulate it efficiently by bundling together many of those operations. The actual code is long and complicated — this is the last problem in a finals round, after all — so we just present an overview of the main idea.

The program can be factorized into 5 parts: A(B)C(D)E. Some of these may be empty; in particular, in the Small dataset, D and E are always empty. Each sequence of simple instructions can be translated, via simulation, into a complex instruction of the form:

1. Let i be the current position of the truck.
2. Add some x_j to position i+j for j in [-2000, 2000]. (2000 is the maximum length of each part.)
3. Move the current position to i+k, where k is also in [-2000, 2000].

Running A
After executing A, only values within 2000 of the starting position can be modified. Let us call the area within 2000 of the starting position the "red" area.

Running (B)
After running B several times, we can either finish or move out of the red area. After several more runs outside, the memory outside the red area will start to look periodic with period |k| and we are going to keep moving the current position according to B's k in the 3rd step until we come back to the red area on the other side, completing a full circle. So, we bundle together all the instructions required to complete the circle and we represent the non-red area as a repetition of a period with length at most 4001 (the range of j's in step 2). We can keep doing this in this way until the loop finishes (which is guaranteed). Notice that after at most 4001 complete circles around the memory, we are going to repeat the initial positions inside the red area. And once we've done that, we are going to start repeating the values there, so we can't do more than 4001 × 256 loops without it being an infinite loop (which is forbidden by input constraints).

Running C
After that, we can simulate C, which can modify the range [-4000, 4000] because the previous loop finished within 2000 of the starting point. Let us call that the "green" area.

Running (D)
When running D, something similar to running B happens, but the memory outside the green area is now the sum of two periodic things with period of size at most 4001, so it can have a period of up to 4001². Luckily, this is still small enough to simulate, and other than that, we can proceed with the same idea as we did for B.

Running E
For E, we proceed again in the same fashion. In this case, the non-periodic area's size can increase to a couple of millions due to the quadratic size of the last period, but that is still well under the memory limits.