Google Code Jam Archive — Round 2 2015 problems
Overview
The problems were much tougher this round; only 10 people got a perfect score! But 500 contestants advance to round 3, so solving problem A and just the small inputs to problems B and C with a fast enough time was sufficient.
Pegman was an easy warmup problem. Over 2000 people solved it! Kiddie Pool was a simple optimization problem that could be solved with some thinking about the structure of the optimal solution. Bilingual was another optimization problem, which could be transformed in a non-obvious way such that it can be solved with a network flow algorithm. Drum Decorator was a difficult dynamic programming problem, which required careful handling of several cases.
Congratulations to everyone who has now advanced to Round 3!
Cast
Problem A. Pegman written and prepared by Ian Tullis.
Problem B. Kiddie Pool written by Bartholomew Furrow. Prepared by Carlos Guía Vera and Ian Tullis.
Problem C. Bilingual written by Bartholomew Furrow. Prepared by John Dethridge, Dustin Tseng, and Ian Tullis.
Problem D. Drum Decorator written by Ian Tullis. Prepared by John Dethridge.
Solutions and other problem preparation by Ahmed Aly, Brian Hirashiki, David Spies, Ian Tullis, Igor Naverniouk, Jackson Gatenby, John Dethridge, Jonathan Wills, Md. Arifuzzaman Arif, Nikolay Kurtov, Petr Mitrichev, Steve Thomas, and Yiming Li.
A. Pegman
Problem
While using Google Street View, you may have picked up and dropped the character Pegman before. Today, a mischievous user is going to place Pegman in some cell of a rectangular grid of unit cells with R rows and C columns. Each of the cells in this grid might be blank, or it might be labeled with an arrow pointing in one of four possible directions: up, right, down, or left.
When Pegman is placed on a grid cell, if that cell is blank, Pegman stands still forever. However, if that cell has an arrow, Pegman starts to walk in that direction. As he walks, whenever he encounters a blank cell, he just keeps walking in his current direction, but whenever he encounters another arrow, he changes to the direction of that arrow and then keeps walking.
You know that it is possible that Pegman might keep happily walking around and around the grid forever, but it is also possible that Pegman's walk will take him over the edge of the grid! You may be able to prevent this and save him by changing the direction of one or more arrows. (Each arrow's direction can only be changed to one of the other three possible directions; arrows can only be changed, not added or removed.)
What is the smallest number of arrows you will need to change to ensure that Pegman will not walk off the edge, no matter where on the grid he is initially placed?
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each begins with one line with two space-separated integers R, C. This line is followed by R lines, each of which has C characters, each of which describes a grid cell and is one of the following:
. period = no arrow
^ caret = up arrow
> greater than = right arrow
v lowercase v = down arrow
< less than = left arrow
Output
For each test case, output one line containing "Case #x: y", where x is the test case number (starting from 1) and y is the minimum number of arrows that must be changed to ensure that Pegman will not leave the grid no matter where he is initially placed, or the text IMPOSSIBLE if it is not possible to ensure this, no matter how many arrows you change.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 100.
Small dataset
Time limit: 240 seconds.
1 ≤ R, C ≤ 4.
Large dataset
Time limit: 480 seconds.
1 ≤ R, C ≤ 100.
Sample
4 2 1 ^ ^ 2 2 >v ^< 3 3 ... .^. ... 1 1 .
Case #1: 1 Case #2: 0 Case #3: IMPOSSIBLE Case #4: 0
In Case #2, no matter where Pegman is placed, he will walk around and around the board clockwise in a circle. No arrows need to be changed.
In Case #3, the mischievous user might place Pegman on the up arrow in the middle of the grid, in which case he will start walking and then walk off the top edge of the grid. Changing the direction of this arrow won't help: it would just make him walk off a different edge.
In Case #4, the only possible starting cell is blank, so Pegman will stand still forever and is in no danger.
B. Kiddie Pool
Problem
A kiddie pool is a big container in which you can put water, so that small children can play in it.
You have access to N different sources of water. The ith source of water produces water at rate Ri and at temperature Ci. Initially, all of the water sources are off. Each source of water can be switched on only once, and switched off only once; the act of switching a source on or off takes no additional time. Multiple sources can be on at the same time.
Your pool can hold an infinite amount of water, but you want to fill the pool to a volume of exactly V with a temperature of exactly X, as quickly as possible. If you turn sources on and off optimally (not every source necessarily has to be used), what's the minimum number of seconds it will take you to do this?
For the purposes of this problem, combining water that has volume V0 and temperature X0 with water that has volume V1 and temperature X1 will instantaneously create water with volume V0+V1 and temperature (V0X0 + V1X1) / (V0 + V1). For example, combining 5L of water at 10 degrees with 10L of water at 40 degrees will result in 15L of water at 30 degrees. You should also assume that water does not heat or cool over time except as a result of being combined with other water.
Input
The first line of the input gives the number of test cases, T. T test cases follow. The first line of each test case contains three space-separated numbers: an integer N, and real numbers V and X as described above.
The next N lines each contain two space-separated real numbers, Ri and Ci, the rate of flow and temperature of the ith water source respectively. The volume is expressed in liters, rates of flow are expressed in liters per second, and temperatures are expressed in degrees Celsius.
All real numbers will be exactly specified to four decimal places.
Output
For each test case, output one line containing "Case #x: y", where x is the test case number (starting from 1) and y is the minimum number of seconds it takes to fill the kiddie pool to the right volume and temperature. If it is impossible to do so given the inputs, y should be the string IMPOSSIBLE.
y will be considered correct if it is within an absolute or relative error of 10-6 of the correct answer. See the FAQ for an explanation of what that means, and what formats of real numbers we accept. You can also read there about the format of our input real numbers, in which the decimal point will be represented by the . character.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 100.
0.1 ≤ X ≤ 99.9.
0.1 ≤ Ci ≤ 99.9.
Small dataset
Time limit: 240 seconds.
1 ≤ N ≤ 2.
0.0001 ≤ V ≤ 100.0.
0.0001 ≤ Ri ≤ 100.0.
Large dataset
Time limit: 480 seconds.
1 ≤ N ≤ 100.
0.0001 ≤ V ≤ 10000.0.
0.0001 ≤ Ri ≤ 10000.0.
Sample
6 1 10.0000 50.0000 0.2000 50.0000 2 30.0000 65.4321 0.0001 50.0000 100.0000 99.9000 2 5.0000 99.9000 30.0000 99.8999 20.0000 99.7000 2 0.0001 77.2831 0.0001 97.3911 0.0001 57.1751 2 100.0000 75.6127 70.0263 75.6127 27.0364 27.7990 4 5000.0000 75.0000 10.0000 30.0000 20.0000 50.0000 300.0000 95.0000 40.0000 2.0000
Case #1: 50.0000000 Case #2: 207221.843687375 Case #3: IMPOSSIBLE Case #4: 0.500000000 Case #5: 1.428034895 Case #6: 18.975332068
In Case #1, the one available source happens to be the exact temperature we need. The optimal strategy is to immediately turn it on and let it run until we have 10 L. Since 0.2 L will come out every second, this takes 50 seconds.
In Case #2, one optimal strategy is to turn on the first source and let it run for 207221.843687375 seconds, and then, about 0.092778156 seconds before the end, also turn on the second source.
In Case #3, both available water sources are cooler than the target temperature, so there is no way to reach it.
C. Bilingual
Problem
Elliot's parents speak French and English to him at home. He has heard a lot of words, but it isn't always clear to him which word comes from which language! Elliot knows one sentence that he's sure is English and one sentence that he's sure is French, and some other sentences that could be either English or French. If a word appears in an English sentence, it must be a word in English. If a word appears in a French sentence, it must be a word in French.
Considering all the sentences that Elliot has heard, what is the minimum possible number of words that he's heard that must be words in both English and French?
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each starts with a single line containing an integer N. N lines follow, each of which contains a series of space-separated "words". Each "word" is made up only of lowercase characters a-z. The first of those N lines is a "sentence" in English, and the second is a "sentence" in French. The rest could be "sentences" in either English or French. (Note that the "words" and "sentences" are not guaranteed to be valid in any real language.)
Output
For each test case, output one line containing "Case #x: y", where x is the test case number (starting from 1) and y is the minimum number of words that Elliot has heard that must be words in both English and French.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 25.
Each word will contain no more than 10 characters.
The two "known" sentences will contain no more than 1000 words each.
The "unknown" sentences will contain no more than 10 words each.
Small dataset
Time limit: 240 seconds.
2 ≤ N ≤ 20.
Large dataset
Time limit: 480 seconds.
2 ≤ N ≤ 200.
Sample
4 2 he loves to eat baguettes il aime manger des baguettes 4 a b c d e f g h i j a b c i j f g h d e 4 he drove into a cul de sac elle a conduit sa voiture il a conduit dans un cul de sac il mange pendant que il conduit sa voiture 6 adieu joie de vivre je ne regrette rien adieu joie de vivre je ne regrette rien a b c d e f g h i j a b c i j f g h d e
Case #1: 1 Case #2: 4 Case #3: 3 Case #4: 8
In Case #2, the last two sentences could either be: English English, English French, French English, or French French. The second of those possibilities is the one that minimizes the number of words common to both languages; that set turns out to be d, e, i, and j.
D. Drum Decorator
Problem
You are the drummer in the rock band Denise and the Integers. Your drum is a cylinder around which you've wrapped a rectangular grid of cells.
Your band is scheduled to perform in Mathland. The Mathlanders are a tough audience, and they will expect every cell of your drum to contain a positive integer; zeroes and negative integers are not allowed. Moreover, each integer K must border (share an edge, and not just a point, with) exactly K other cells with the same integer -- that is, a cell with a 1 must touch exactly one other cell with a 1, a cell with a 2 must touch exactly 2 other cells with a 2, and so on. Apart from this restriction, it does not matter what other cells a cell touches. (The circular top and bottom of the drum do not count as cells and do not need to be decorated. Note that this means that the cells along the top and bottom of the drum only touch three other cells each, whereas all the other cells touch four other cells each.)
For example, this is a valid decoration of a cylinder formed by a grid with 3 rows and 5 columns:
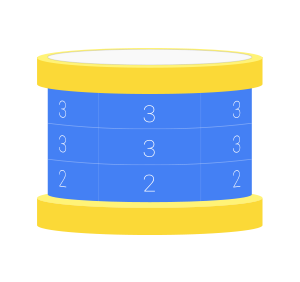
(Imagine that the unseen two columns on the back of the drum are the same as the three visible columns.)
You want to know how many different valid decorations are possible. Two decorations are different if one cannot be rotated (around the cylinder's axis of symmetry) to produce the other. The top and bottom of a drum are considered different, so this decoration of a 3x5 grid is different from the one above:
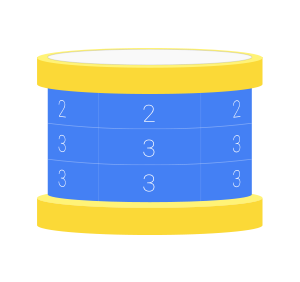
(Again, imagine that the unseen two columns on the back of the drum are the same as the three visible columns.)
Your drum has R rows and C columns. How many different valid decorations are possible? The number may be large, so return the number of decorations modulo 109 + 7 (1000000007).
Input
The first line of the input gives the number of test cases, T. T lines follow; each contains two space-separated integers, R and C, which are the number of rows and columns in the drum.Output
For each test case, output one line containing "Case #x: y", where x is the test case number (starting from 1) and y is the number of valid decorations modulo 109 + 7, as described above.
Limits
Memory limit: 1 GB.
Small dataset
Time limit: 240 seconds.
1 ≤ T ≤ 20.
2 ≤ R ≤ 6.
3 ≤ C ≤ 6.
Large dataset
Time limit: 480 seconds.
1 ≤ T ≤ 100.
2 ≤ R ≤ 100.
3 ≤ C ≤ 100.
Sample
2 2 4 3 5
Case #1: 1 Case #2: 2
In Case #2, the only two solutions are the two depicted in the problem statement.
Analysis — A. Pegman
IMPOSSIBLE.
Analysis — B. Kiddie Pool
While the pool is being filled, each source of water is turned on for some fraction of the time. This is equivalent to having each source turned on for the whole time at a fixed rate which is between zero and Ri. So the problem is to find what rate each source should be set to in order to maximize the total flow and get the correct temperature. Then the fill time is the capacity of the pool divided by the total flow rate.
Find the temperature of the water we get when setting each source's rate to the maximum. If the temperature is exactly the desired temperature, then we have the solution.
If the temperature is too hot, then we need to lower the temperature by lowering the flow rate of some of the sources. To lower the total flow by as little as possible, we decrease flow starting with the hottest source, moving to the cooler sources if necessary, until the average temperature of the flowing water equals the desired temperature. If we never reach the desired temperature, then no solution was possible.
If the temperature is too low when all the sources are set to their maximum rate, then the solution is similar — we raise the temperature by reducing the flow rate of sources, starting from the coldest source.
Analysis — C. Bilingual
Construct a graph with a node for each sentence and word. For each sentence S, add edges in the graph between the node for S and each of the nodes for the words in S.
Now consider a path in the graph from sentence 0 to sentence 1. The nodes on the path will alternate between sentences and words. Since the language of the sentences in the path must at some point change from English to French, one of the words along the path must belong to both languages. We need to find a minimal set of words such that every path from sentence 0 to sentence 1 in the graph goes through one of the words in the set. This is equivalent to finding a minimal vertex cut in the graph, where the cut vertices can only include the nodes for words.
We can solve this by transforming the problem into an edge cut problem in a directed graph. For each word w, create two nodes Aw and Bw. Add a directed edge from Aw to Bw with capacity 1, and for each sentence S which contains w, add directed edges from S to Aw and from Bw to S, both with infinite capacity.
Now we find the size of the minimum cut using a maximum flow algorithm, and the max-flow min-cut theorem. Each edge in the cut will cut the edge from Aw to Bw for some word w, since those are the only finite-capacity edges. These words form a minimal set of bilingual words which solves the problem.
Analysis — D. Drum Decorator
Some important initial insights are:
- A cell can only take three values: 1, 2, or 3. 4s would have to keep propagating until they hit an edge cell, and edge cells only border three other cells.
- If a 3 appears, it must be in a band of 2 complete rows. To see this, place a 3 along the border of the top of the drum, and note that the 3 adjacent cells must all contain 3s. This must continue all the way around the top, which also fills up the row below. Suppose that some other finite arrangement of 3s was valid — then there must be a highest 3 in the pattern, above which no other 3 can be placed, but then that 3 can only be part of a set of 2 rows of 3s, by the same argument above.
- If a 2 appears, it must be either in a 2x2 square of 2s, or in a (possibly winding) line of 2s that goes all the way around the drum and reconnects with itself.
- 1s can only appear in adjacent "dominoes" of two.
Besides the bands of 3s, there are four patterns using 1s and 2s:
I. one-thick bands of 2s:
2...
II. alternating upright dominoes of 1s and 2x2 squares of 2s:
122...
122...
III. a line of 2s winding around horizontal dominoes of 1s:
222112...
112222...
IV. a line of 2s winding around vertical dominoes of 1s:
2212...
1212...
1222...
None of these patterns can border each other, but they can be separated by bands of 3s. The number of columns in a drum can rule out some patterns -- II, III, and IV require multiples of 3, 6, and 4, respectively.
Now we can use dynamic programming to assign patterns to the drum. Our state is how many rows we have filled, and whether the previous pattern was a pair of rows of 3s.
Each of the five patterns repeat with some period P, which is either 1, 3, 4 or 6, so there are P ways to place that pattern on the drum.
Each overall drum assignment also has a period, which is the least common multiplier of the periods of all of the patterns on it.
An extra complication is that drum assignments that are rotations of each other should only be counted once. So our dynamic programming state should also include the period of the current drum assignment. When counting the final number of solutions, we divide the number of solutions in each state by the state's period. For example, if we have 18 ways to produce a solution of period 3, this only corresponds to 6 solutions.
Another way to handle equivalent patterns is to use Burnside's lemma. We leave the details as an exercise to the reader!