Google Code Jam Archive — Round 1B 2015 problems
Overview
Round 1B was considerably tougher than Round 1A, with no clear “easy” Large input. Counter Culture is solvable using a fairly simple algorithm, but it’s not trivial to get the details right, and 31% of attempts on the Large input failed. Noisy Neighbors is an ad hoc problem that requires some clever insight to see the correct strategy, and there's a corner case that is easy to overlook. Hiking Deer was very challenging for a Round 1 problem -- its second Small input was worth more than each of the other two problems’ Large inputs! Its Large, which set a daunting bar of up to 500000 hikers per test case, was designed to weed out all but the very fastest solutions; only 88 contestants dared to attempt it, of which 52 got it right.
5619 contestants downloaded at least one input, and at the end of the day, 60.5% of the contestants solved at least one Small or Large input. To advance, it was generally necessary to solve at least three inputs, including at least one Large. Only 30 people (including our defending world champion) got a perfect score.
We hope everybody enjoyed the round! Congratulations to the Top 1000 who have now made it to Round 2.
Cast
Problem A. Counter Culture written and prepared by Ian Tullis.
Problem B. Noisy Neighbors written by Ian Tullis. Prepared by Ahmed Aly.
Problem C. Hiking Deer written by Ian Tullis. Prepared by Yiming Li.
Solutions and other problem preparation by Ahmed Aly, Artur Satayev, Calvin Li, Carlos Guía Vera, David Spies, Felix Halim, Ian Tullis, Igor Naverniouk, Ilham Kurnia, Jackson Gatenby, John Dethridge, Jonathan Paulson, Onufry Wojtaszczyk, Tsung-Hsien Lee, and Yiming Li.
Contest analysis written by John Dethridge, Artur Satayev, Felix Halim, David Spies, and Ian Tullis.
A. Counter Culture
Problem
In the Counting Poetry Slam, a performer takes the microphone, chooses a number N, and counts aloud from 1 to N. That is, she starts by saying 1, and then repeatedly says the number that is 1 greater than the previous number she said, stopping after she has said N.
It's your turn to perform, but you find this process tedious, and you want to add a twist to speed it up: sometimes, instead of adding 1 to the previous number, you might reverse the digits of the number (removing any leading zeroes that this creates). For example, after saying "16", you could next say either "17" or "61"; after saying "2300", you could next say either "2301" or "32". You may reverse as many times as you want (or not at all) within a performance.
The first number you say must be 1; what is the fewest number of numbers you will need to say in order to reach the number N? 1 and N count toward this total. If you say the same number multiple times, each of those times counts separately.
Input
The first line of the input gives the number of test cases, T. T lines follow. Each has one integer N, the number you must reach.
Output
For each test case, output one line containing "Case #x: y", where x is the test case number (starting from 1) and y is the minimum number of numbers you need to say.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 100.
Small dataset
Time limit: 240 seconds.
1 ≤ N ≤ 106.
Large dataset
Time limit: 480 seconds.
1 ≤ N ≤ 1014.
Sample
3 1 19 23
Case #1: 1 Case #2: 19 Case #3: 15
In Case #3, the optimal strategy is to count up to 12, flip to 21, and then continue counting up to 23. That is, the numbers you will say are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 21, 22, 23.
B. Noisy Neighbors
Problem
You are a landlord who owns a building that is an R x C grid of apartments; each apartment is a unit square cell with four walls. You want to rent out N of these apartments to tenants, with exactly one tenant per apartment, and leave the others empty. Unfortunately, all of your potential tenants are noisy, so whenever any two occupied apartments share a wall (and not just a corner), this will add one point of unhappiness to the building. For example, a 2x2 building in which every apartment is occupied has four walls that are shared by neighboring tenants, and so the building's unhappiness score is 4.
If you place your N tenants optimally, what is the minimum unhappiness value for your building?
Input
The first line of the input gives the number of test cases, T. T lines follow; each contains three space-separated integers: R, C, and N.
Output
For each test case, output one line containing "Case #x: y", where x is the test case number (starting from 1) and y is the minimum possible unhappiness for the building.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 1000.
0 ≤ N ≤ R*C.
Small dataset
Time limit: 240 seconds.
1 ≤ R*C ≤ 16.
Large dataset
Time limit: 480 seconds.
1 ≤ R*C ≤ 10000.
Sample
4 2 3 6 4 1 2 3 3 8 5 2 0
Case #1: 7 Case #2: 0 Case #3: 8 Case #4: 0
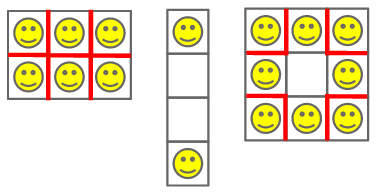
In Case #2, there are various ways to place the two tenants so that they do not share a wall. One is illustrated below.
In Case #3, the optimal strategy is to place the eight tenants in a ring, leaving the middle apartment unoccupied.
Here are illustrations of sample cases 1-3. Each red wall adds a point of unhappiness.
C. Hiking Deer
Problem
Herbert Hooves the deer is going for a hike: one clockwise loop around his favorite circular trail, starting at degree zero. Herbert has perfect control over his speed, which can be any nonnegative value (not necessarily an integer) at any time -- he can change his speed instantaneously whenever he wants. When Herbert reaches his starting point again, the hike is over.
The trail is also used by human hikers, who also walk clockwise around the trail. Each hiker has a starting point and moves at her own constant speed. Humans continue to walk around and around the trail forever.
Herbert is a skittish deer who is afraid of people. He does not like to have encounters with hikers. An encounter occurs whenever Herbert and a hiker are in exactly the same place at the same time. You should consider Herbert and the hikers to be points on the circumference of a circle.
Herbert can have multiple separate encounters with the same hiker.
If more than one hiker is encountered at the same instant, all of them count as separate encounters.
Any encounter at the exact instant that Herbert finishes his hike still counts as an encounter.
If Herbert were to have an encounter with a hiker and then change his speed to exactly match that hiker's speed and follow along, he would have infinitely many encounters! Of course, he must never do this.
Encounters do not change the hikers' behavior, and nothing happens when hikers encounter each other.
Herbert knows the starting position and speed of each hiker. What is the minimum number of encounters with hikers that he can possibly have?
Solving this problem
Usually, Google Code Jam problems have 1 Small input and 1 Large input. This problem has 2 Small inputs and 1 Large input. You must solve the first Small input before you can attempt the second Small input; as usual, you will be able to retry the Small inputs (with a time penalty). Once you have solved both Small inputs, you will be able to download the Large input; as usual, you will get only one chance at the Large input.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each begins with one line with an integer N, and is followed by N lines, each of which represents a group of hikers starting at the same position on the trail. The ith of these lines has three space-separated integers: a starting position Di (representing Di/360ths of the way around the trail from the deer's starting point), the number Hi of hikers in the group, and Mi, the amount of time (in minutes) it takes for the fastest hiker in that group to make each complete revolution around the circle. The other hikers in that group each complete a revolution in Mi+1, Mi+2, ..., Mi+Hi-1 minutes. For example, the line
180 3 4
would mean that three hikers begin halfway around the trail from the deer's starting point, and that they take 4, 5, and 6 minutes, respectively, to complete each full revolution around the trail.
Herbert always starts at position 0 (0/360ths of the way around the circle), and no group of hikers does. Multiple groups of hikers may begin in the same place, but no two hikers will both begin in the same place and have the same speed.
Output
For each test case, output one line containing "Case #x: y", where x is the test case number (starting from 1) and y is the minimum number of encounters with hikers that the deer can have.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 100.
1 ≤ Di ≤ 359.
1 ≤ N ≤ 1000.
1 ≤ Hi.
1 ≤ Mi ≤ 109. (Note that this only puts a cap on the time required for the fastest hiker in each group to complete a revolution. Slower hikers in the group will take longer.)
Small dataset 1
Time limit: 240 seconds.
The total number of hikers in each test case will not exceed 2.
Small dataset 2
Time limit: 240 seconds.
The total number of hikers in each test case will not exceed 10.
Large dataset
Time limit: 480 seconds.
The total number of hikers in each test case will not exceed 500000.
Sample
3 4 1 1 12 359 1 12 2 1 12 358 1 12 2 180 1 100000 180 1 1 1 180 2 1
Case #1: 0 Case #2: 1 Case #3: 0
In Case #2, the second hiker is moving much faster than the first, and if Herbert goes slowly enough to avoid overtaking the first hiker, he will have multiple encounters with the speedy second hiker. One optimal strategy for Herbert is to go exactly as fast as the second hiker, encountering the first hiker once and never encountering the second hiker at all.
In Case #3, the two hikers start in the same place, but one is twice as fast as the other. One optimal strategy is for Herbert to immediately catch up to the slower hiker without overtaking him, follow just behind him until he passes the deer's starting position, and then finish quickly before the faster hiker can catch Herbert.
Analysis — A. Counter Culture
For the small dataset, it suffices to use a breadth-first search to find the minimum number of moves required to generate all numbers from 1 to 106. You will never want to construct a number larger than 106 and later flip it to get a smaller number, so you only need to consider 106 states.
For the large dataset, the following solution works. The key ideas are:
- You should first build the numbers 10, 100, 1000, ... until you get a power of 10 with the same number of digits as N, and then build N.
- You should make at most one flip while the number is at a given number of digits.
Our algorithm works in two parts.
Part 1: Get to the right number of digits as fast as possible.
To get from a 1 followed by X 0s to a 1 followed by X+1 0s: first count until the right half of the number is filled with 9s. (When the length is odd, make the left half shorter than the right half.) Then flip, then count until the number is all 9s. Then add 1. (To get from 1 to 10, obviously we don't need to flip.)
Part 2: Either count directly to the answer, or do some counting, flip, and then do some more counting, whichever is faster.
Once we're at the right number of digits, we use a similar algorithm to produce N: count until the right half looks like the left half of N in reverse, then flip, then count up to the target. For example, to get from 100000 to 123456:
- count to 100321
- flip to get 123001
- count to 123456.
If the left half is just a 1 followed by 0s, we can skip the first two steps and just count to N.
When the right half of N is all zeroes the above method doesn't work, because after we flip, the right half ends with 1. Instead, we make the right half look like the left half of N-1, flip, then count up to N. For example, to get from 100000 to 300000:
- count to 100992
- flip to get 299001
- count to 300000.
However, as before, if the left half of N-1 is a 1 followed by 0s, we can skip the first two steps. For example, to get from 100000 to 101000, it's best to count up directly.
Why do we need to do at most one flip? The goal of the flip is to allow us to reach the left half of the number as quickly as possible. Raising the right half to the desired value is better done by directly counting the number up. In other words, there is no added value in doing multiple flips.
Sample implementation in C++:
#include <cstdio>
#include <cstdlib>
#include <string>
#include <algorithm>
using namespace std;
long long p10[10]; // p10[i] == 10^i
bool is_1_followed_by_0s(string S) {
reverse(S.begin(), S.end());
return atoi(S.c_str()) == 1;
}
int solve(long long N) {
if (N < 10) return N; // Trivial case.
char X[20]; sprintf(X, "%lld", N);
string S = X;
int M = S.length(); // Number of digits of N.
// Starts from 1.
int ans = 1;
// Part 1: from 1, get to the M digits as fast as possible.
for (int d = 1; d < M; d++) {
// For digits = 7, it starts from 7 digits: 1000000
ans += p10[(d + 1) / 2] - 1; // Count up 9999: 1009999
if (d > 1) ans++; // Flip once: 9999001
ans += p10[d / 2] - 1; // Count up 999: 10000000
}
// Part 2:
// Split N into two halves. For example N = "1234567"
string L = S.substr(0, M / 2); // L = "123"
string R = S.substr(M / 2); // R = "4567"
// Handles the case where the right half is all zeroes.
if (atoi(R.c_str()) == 0) return solve(N - 1) + 1;
// Special case: Count directly to the answer.
if (is_1_followed_by_0s(L))
return ans + atoi(R.c_str());
// Count until the right half looks like the left half of N
// in reverse. In this case, count from 1000000 to 1000321.
reverse(L.begin(), L.end());
ans += atoi(L.c_str());
// Flip 1000321 to 1230001.
ans++;
// Count up 4566 to the target from 1230001 to 1234567.
ans += atoi(R.c_str()) - 1;
return ans;
}
int main() {
p10[0] = 1;
for (int i = 1; i < 10; i++)
p10[i] = p10[i - 1] * 10;
long long T, N;
scanf("%lld", &T);
for (int TC = 1; TC <= T; TC++) {
scanf("%lld", &N);
printf("Case #%d: %d\n", TC, solve(N));
}
}
Analysis — B. Noisy Neighbors
Small number of tenants, N <= ceil(R * C / 2)
For N <= ceil(R * C / 2), we can put the tenants in a checkerboard pattern inside the R x C apartment complex and get the minimum possible unhappiness score of zero. See the following examples:
.X.X .X.X. X.X.X
X.X. X.X.X .X.X.
.X.X .X.X. X.X.X
X.X. X.X.X .X.X.
X.X.X
4 x 4 4 x 5 5 x 5
The left figure shows a 4 x 4 complex where we can place up to 8 tenants to apartments marked by ‘X’ and get zero unhappiness score (an empty apartment is marked by ‘.’). Observe that no two occupied apartments share a wall. Similarly for the middle figure, we can place up to 10 tenants and get zero unhappiness score.
With either R or C even (the left and middle figures), exactly half of the apartments can be rented. However, when both R and C are odd, two checkerboard patterns are possible. We should pick the checkerboard pattern with larger size. So for the right figure, we pick the checkerboard that has 13 ‘X’ marks, instead of the other checkerboard with only 12 ‘X’ marks.
Large number of tenants, N > ceil(R * C / 2)
For N > ceil(R * C / 2), some level of unhappiness will be present, since we must place at least one pair of tenants next to each other. Instead of starting with an empty building and adding tenants, it is easier to solve this case by starting with a building completely filled with tenants, and then removing K = R*C - N of them. We now need to determine which K tenants to remove in order to decrease the unhappiness score by as much as possible.
Let’s first solve the smaller cases where R = 1 or C = 1. For those cases, we can always remove up to K tenants in such a way that each removal decreases the unhappiness score by 2, which is the maximum possible, and thus is optimal. To show this, look at the two possible examples below where C is even and C is odd:
.X.X.. .X.X.X. even C=6 odd C=7
For even C, K is at most C / 2 - 1 since N > ceil(R * C / 2). Thus for even C, it is always possible to remove tenants using the pattern shown on the left figure (marked by ‘X’) to guarantee that each removal decreases the unhappiness score by 2 (i.e., the maximum possible decrease).
For odd C, K is at most (C - 1) / 2. In this case, it is always possible to remove tenants using the pattern shown on the right figure (marked by ‘X’) to guarantee that each removal decreases the unhappiness score by 2 (i.e., the maximum possible decrease).
To get some idea for solving a general case where R and C are at least 2, let’s observe the four buildings below with the checkerboard pattern. The cells marked by a number represent the apartments where the tenants may be removed. The numbers represent the amount of unhappiness each tenant is contributing to the building, or equivalently, the decrease in unhappiness that will occur if those tenants were removed:
.3.2 .3.3. 2.3.2 .3.3.
3.4. 3.4.3 .4.4. 3.4.3
.4.3 .4.4. 3.4.3 .4.4.
2.3. 2.3.2 .4.4. 3.4.3
2.3.2 .3.3.
4 x 4 4 x 5 5 x 5 5 x 5
We can devise an optimal K-tenant-removal strategy (i.e., remove K tenants such that the total unhappiness score is minimal) as follows:
- For K <= (R - 2) * (C - 2) / 2, we can always remove K tenants from the inner building (at the positions marked by ‘4’ in the figures) where each tenant removal decreases the unhappiness score by 4, which is the maximum decrease we can get, and thus it is optimal.
- For K > (R - 2) * (C - 2) / 2, after removing all the tenants at positions marked by ‘4’, we start removing more tenants at the sides of the building marked by ‘3’ (each tenant removal at these positions decreases the unhappiness score by 3). If all tenants at the sides of the building have been removed but we still need to remove more tenants (i.e., the total number of removed tenants has not reached K yet), remove more tenants at the corners of the building marked by ‘2’ (each tenant removal at these positions decreases the unhappiness score by 2). It is guaranteed that K tenants can be removed by now, since K is at most R * C / 2.
Note that for odd R and odd C, there are two possible checkerboard patterns. Both of them must be considered, and we pick the one that yields the minimum unhappiness score.
Why does this strategy work?
Each removal can reduce unhappiness by at most 4. Below is a 5 x 5 building where the number in each apartment cell is the amount of unhappiness score reduction if the tenant at that cell location is removed:
23332 34443 34443 34443 23332
We can place at most ceil((R-2) * (C-2) / 2) 4s, so we cannot do better than to place this many 4s, and for the remainder place 3s. So we can put an upper bound U on the amount of unhappiness reduction we can achieve — U <= 4 * K for K <= ceil((R-2) * (C-2) / 2), and U <= 3 * K + ceil((R-2) * (C-2) / 2) otherwise.
Consider the removal strategy using this checkerboard pattern (let's call this pattern1):
2.3.2 .4.4. 3.4.3 .4.4. 2.3.2
This achieves U exactly when K <= floor(R * C / 2) - 3 for R and C odd, and K <= floor(R * C / 2) - 2 when one of R and C are even, so this strategy is optimal for these cases.
For the remaining cases, this strategy achieves either U-1 and U-2, because we need to place some 2s. Since this strategy uses the maximal number of 4s, and the maximal number of 3s possible when using the maximal number of 4s, the only possible way to improve upon it would be to use 1 fewer 4 in order to use more 3s.
It is indeed possible to do this to improve the case K = floor(R * C / 2) - 1 from 4 total unhappiness to 3 total unhappiness, using the other checkerboard pattern (let’s call this pattern2):
.3.3. 3.4.3 .4.4. 3.4.3 .3.3.
That is, if we were to use the checkerboard pattern1, removing K = 11 tenants reduces the unhappiness score by 5*4 + 4*3 + 2*2 = 36. On the other hand, pattern2 reduces the unhappiness score by 4*4 + 7*3 = 37, by using 1 fewer 4s and more 3s.
On the other hand, pattern1 is optimal is when K = 5, for example. In this case, pattern1 reduces the unhappiness score more than pattern2 since pattern1 has 5 of 4s while pattern2 only has 4 of 4s and would need to remove another 1 of 3s.
Sample implementation in C++:
#include <cassert>
#include <cstdio>
#include <algorithm>
using namespace std;
int T, R, C, N;
int remove_tenants(int &K, int max_remove, int remove_cost) {
int removed = min(K, max_remove);
K -= removed;
return removed * remove_cost;
}
int get_score(int all, int corners, int inners) {
int sides = all - corners - inners;
int K = R * C - N;
int unhappiness = R * C * 2 - R - C;
unhappiness -= remove_tenants(K, inners, 4);
unhappiness -= remove_tenants(K, sides, 3);
unhappiness -= remove_tenants(K, corners, 2);
assert(K == 0);
return unhappiness;
}
int min_unhappines() {
// Guaranteed zero unhappiness.
if (N <= (R * C + 1) / 2) return 0;
if (R == 1) {
int K = R * C - N;
int unhappiness = C - 1;
int remove_cost = 2;
return unhappiness - K * remove_cost;
}
if (R % 2 == 1 && C % 2 == 1) {
// 2.3.2
// .4.4.
// 3.4.3
// .4.4.
// 2.3.2
int pattern1 = get_score(
(R * C + 1) / 2, // Max #tenants that can be removed.
4, // #tenants at the corners of the building.
((R-2) * (C-2) + 1) / 2 // #tenants at inner building.
);
// .3.3.
// 3.4.3
// .4.4.
// 3.4.3
// .3.3.
int pattern2 = get_score(
(R * C) / 2, // Max #tenants that can be removed.
0, // #tenants at the corners of the building.
((R-2) * (C-2)) / 2 // #tenants at inner building.
);
return min(pattern1, pattern2);
}
// .3.2 2.3. 2.3.2
// 3.4. or .4.3 or .4.4.
// .4.3 3.4. 3.4.3
// 2.3. .3.2 .3.3.
return get_score(
(R * C + 1) / 2, // Max #tenants that can be removed.
2, // #tenants at the corners of the building.
((R-2) * (C-2) + 1) / 2 // #tenants at inner building.
);
}
int main() {
scanf("%d", &T);
for (int TC = 1; TC <= T; TC++) {
scanf("%d %d %d", &R, &C, &N);
if (R > C) swap(R, C);
printf("Case #%d: %d\n", TC, min_unhappines());
}
}
Analysis — C. Hiking Deer
Some programming contest problems have their origins in everyday life. This year, the Qualification Round's "Standing Ovation" was written during a concert, and Round 1A's "Haircut" was written while waiting in a long line for a sandwich at Google's Go Cafe. You may not be surprised to learn that this problem was inspired by a circular hike on a day with an unusually large number of hikers on the trail!
Let H be the total number of hikers. One important observation is that the answer can't be larger than H, since no matter what the hikers' initial positions and speeds are, Herbert can just go around so fast that no hiker gets a chance to move very far, so he encounters each of them once.
Another key observation is that allowing Herbert to wait or vary his speed makes no difference to the answer. If we know the time he arrives at the end, we can put a lower bound on the answer based on the number of hikers he must have overtaken and the number of times hikers must have overtaken him. This lower bound is exactly the answer we get by having Herbert move at a constant speed, so no strategy of waiting or changing speed can improve on it.
So now, we will find a finish time that minimizes the number of encounters.
Consider the case of a single hiker. As the trail is circular and the hiker walks endlessly, the hiker repeatedly reaches Herbert’s starting point. Call the time at which Herbert finishes his hike X, and the times when the hiker reaches Herbert’s starting point T1, T2, T3, etc.
- If X <= T1, then there is one encounter with the hiker as Herbert passes.
- If T1 < X < T2, then there are no encounters with the hiker.
- If T2 <= X < T3, then the hiker passes Herbert once.
- If T3 <= X < T4, then the hiker passes Herbert twice.
- etc.
So as we increase Herbert's finish time, there are multiple "events" where the number of encounters changes. It decreases by 1 for the first event, then it increases by 1 for each event after that.
Now when we have multiple hikers, there is a series of events for each of them that can increase or decrease the total number of encounters.
There will never be a reason for Herbert to take so long that we see more than H events for a single hiker, because then the number of encounters with that single hiker will be at least H. So a solution that will work for the small datasets is to make a sorted list of the first H events for all of the hikers, and then find the optimal number of encounters in this way:
- Initialize the number of encounters to H.
- For each event, in order of time, subtract 1 from the number of encounters if it is the first event for the hiker, otherwise add 1.
The answer is the minimum number of encounters for any time.
For the large dataset, we need a more efficient solution. Note that there are only H events that subtract 1 from the number of encounters, and the rest add 1. So once we have processed 2H events, we will never find a time with fewer than H encounters, so we can stop searching.
We still need to avoid storing H^2 events. To do this, we can maintain a priority queue of events. We initialize the queue with one event for each hiker -- the event for that hiker's T1. Whenever we process an event, we replace that event on the queue with the next event for that hiker. In this way we only need O(H) memory, and O(H log H) time.
One subtlety to note is that if multiple hikers reach Herbert’s starting point at the same time, we must process the events that add an encounter (those for a hiker's T2, T3, etc.) before the events that subtract an encounter (those for a hiker's T1) since the number of encounters only really decreases once Herbert's finish time is larger than T1.
52 people successfully solved the large input for this problem during the contest. See, for example, Belonogov's solution, which you can download from the scoreboard.