Google Code Jam Archive — Round 1A 2015 problems
Overview
Round 1A has 5686 contestants who downloaded at least one input. Contestants faced three challenging problems: Mushroom Monster where Bartholomew wants to determine Kaylin’s minimum rate of eating mushrooms using two different methods (based on a true story!). With 98% correct attempts on the Large input. Haircut was a tricky binary search problem, with the danger of off-by-one errors, and unlike problem A, had only 64% correct attempts of the Large input. The toughest problem was Logging for which contestants needed computational geometry. Most contestants needed everything but C-large to advance, although some solved all of C or C-small plus all of B, or just solved all of A and B very fast.
At the end of the day, 88% of our contestants solved at least one input, and 323 people got everything right (That is really a huge number!).
We hope everybody enjoyed the round! Congratulations to the Top 1000, who have now made it to Round 2; and to everyone else, we'll see you in Rounds 1B and 1C!
Cast
Problem A. Mushroom Monster written by Bartholomew Furrow, prepared by Greg Tener, analysis written by Felix Halim.
Problem B. Haircut written by Ian Tullis, prepared by Steve Thomas, analysis written by Artur Satayev.
Problem C. Logging written by John Dethridge, prepared by David Spies, analysis written by John Dethridge.
Solutions and other problem preparations and reviews by Ahmed Aly, Chieu Nguyen, David Gómez Cermeño, David Spies, Dustin Tseng, Felix Halim, Ian Tullis, Igor Naverniouk, Ilham Kurnia, Jackson Gatenby, John Dethridge, Jonathan Shen, Luis Giro Valdes, Risan, Taman (Muhammed) Islam, and Topraj Gurung.
A. Mushroom Monster
Problem
Kaylin loves mushrooms. Put them on her plate and she'll eat them up! In this problem she's eating a plate of mushrooms, and Bartholomew is putting more pieces on her plate.
In this problem, we'll look at how many pieces of mushroom are on her plate at 10-second intervals. Bartholomew could put any non-negative integer number of mushroom pieces down at any time, and the only way they can leave the plate is by being eaten.
Figure out the minimum number of mushrooms that Kaylin could have eaten using two different methods of computation:
- Assume Kaylin could eat any number of mushroom pieces at any time.
- Assume that, starting with the first time we look at the plate, Kaylin eats mushrooms at a constant rate whenever there are mushrooms on her plate.
For example, if the input is 10 5 15 5:
With the first method, Kaylin must have eaten at least 15 mushroom pieces: first she eats 5, then 10 more are put on her plate, then she eats another 10. There's no way she could have eaten fewer pieces.
With the second method, Kaylin must have eaten at least 25 mushroom pieces. We can determine that she must eat mushrooms at a rate of at least 1 piece per second. She starts with 10 pieces on her plate. In the first 10 seconds, she eats 10 pieces, and 5 more are put on her plate. In the next 5 seconds, she eats 5 pieces, then her plate stays empty for 5 seconds, and then Bartholomew puts 15 more pieces on her plate. Then she eats 10 pieces in the last 10 seconds.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each will consist of one line containing a single integer N, followed by a line containing N space-separated integers mi; the number of mushrooms on Kaylin's plate at the start, and at 10-second intervals.
Output
For each test case, output one line containing "Case #x: y z", where x is the test case number (starting from 1), y is the minimum number of mushrooms Kaylin could have eaten using the first method of computation, and z is the minimum number of mushrooms Kaylin could have eaten using the second method of computation.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 100.
Small dataset
Time limit: 240 seconds.
2 ≤ N ≤ 10.
0 ≤ mi ≤ 100.
Large dataset
Time limit: 480 seconds.
2 ≤ N ≤ 1000.
0 ≤ mi ≤ 10000.
Sample
4 4 10 5 15 5 2 100 100 8 81 81 81 81 81 81 81 0 6 23 90 40 0 100 9
Case #1: 15 25 Case #2: 0 0 Case #3: 81 567 Case #4: 181 244
B. Haircut
Problem
You are waiting in a long line to get a haircut at a trendy barber shop. The shop has B barbers on duty, and they are numbered 1 through B. It always takes the kth barber exactly Mk minutes to cut a customer's hair, and a barber can only cut one customer's hair at a time. Once a barber finishes cutting hair, he is immediately free to help another customer.
While the shop is open, the customer at the head of the queue always goes to the lowest-numbered barber who is available. When no barber is available, that customer waits until at least one becomes available.
You are the Nth person in line, and the shop has just opened. Which barber will cut your hair?
Input
The first line of the input gives the number of test cases, T. T test cases follow; each consists of two lines. The first contains two space-separated integers B and N -- the number of barbers and your place in line. The customer at the head of the line is number 1, the next one is number 2, and so on. The second line contains
Output
For each test case, output one line containing "Case #x: y", where x is the test case number (starting from 1) and y is the number of the barber who will cut your hair.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 100.
1 ≤ N ≤ 109.
Small dataset
Time limit: 240 seconds.
1 ≤ B ≤ 5.
1 ≤ Mk ≤ 25.
Large dataset
Time limit: 480 seconds.
1 ≤ B ≤ 1000.
1 ≤ Mk ≤ 100000.
Sample
3 2 4 10 5 3 12 7 7 7 3 8 4 2 1
Case #1: 1 Case #2: 3 Case #3: 1
In Case #1, you are the fourth person in line, and barbers 1 and 2 take 10 and 5 minutes, respectively, to cut hair. When the shop opens, the first customer immediately has the choice of barbers 1 and 2, and she will choose the lowest-numbered barber, 1. The second customer will immediately be served by barber 2. The third customer will wait since there are no more free barbers. After 5 minutes, barber 2 will finish cutting the second customer's hair, and will serve the third customer. After 10 minutes, both barbers 1 and 2 will finish; you are next in line, and you will have the choice of barbers 1 and 2, and will choose 1.
C. Logging
Problem
A certain forest consists of N trees, each of which is inhabited by a squirrel.
The boundary of the forest is the convex polygon of smallest area which contains every tree, as if a giant rubber band had been stretched around the outside of the forest.
Formally, every tree is a single point in two-dimensional space with unique coordinates (Xi, Yi), and the boundary is the convex hull of those points.
Some trees are on the boundary of the forest, which means they are on an edge or a corner of the polygon. The squirrels wonder how close their trees are to being on the boundary of the forest.
One at a time, each squirrel climbs down from its tree, examines the forest, and determines the minimum number of trees that would need to be cut down for its own tree to be on the boundary. It then writes that number down on a log.
Determine the list of numbers written on the log.
Input
The first line of the input gives the number of test cases, T. T test cases follow; each consists of a single line with an integer N, the number of trees, followed by N lines with two space-separated integers Xi and Yi, the coordinates of each tree. No two trees will have the same coordinates.
Output
For each test case, output one line containing "Case #x:", followed by N lines with one integer each, where line i contains the number of trees that the squirrel living in tree i would need to cut down.
Limits
Memory limit: 1 GB.
-106 ≤ Xi, Yi ≤ 106.
Small dataset
Time limit: 240 seconds.
1 ≤ T ≤ 100.
1 ≤ N ≤ 15.
Large dataset
Time limit: 480 seconds.
1 ≤ T ≤ 14.
1 ≤ N ≤ 3000.
Sample
2 5 0 0 10 0 10 10 0 10 5 5 9 0 0 5 0 10 0 0 5 5 5 10 5 0 10 5 10 10 10
Case #1: 0 0 0 0 1 Case #2: 0 0 0 0 3 0 0 0 0
Analysis — A. Mushroom Monster
Each method can be solved independently because they answer different questions. With the first method, Kaylin can eat any number of mushroom pieces at any time. Since the only way mushrooms can leave the plate is by being eaten, whenever we see a decrease in the number of mushrooms (in an interval) it must be because they were eaten by Kaylin. The minimum number of mushrooms Kaylin could have eaten using this method is the sum of the observable decreases for each interval. Since we only care about how many mushrooms Kaylin ate, we do not need to calculate how many mushrooms Bartholomew added.
With the second method, Kaylin always eats mushrooms at a constant rate whenever there are mushrooms on her plate. For each interval, we can observe Kaylin’s eat-rate (i.e., the decrease of the number of mushrooms for that time interval). Since we want to find the minimum number of mushrooms Kaylin could have eaten, we should find Kaylin’s minimum eat-rate. Since the eat-rate must be constant for each interval from the beginning until the end, only the highest observable eat-rate makes sense. It may appear that Kaylin eats fewer mushrooms than her eat-rate in some intervals, either because her plate becomes empty during the interval and she stops eating, or because Bartholomew added more mushrooms during the interval.
The number of mushrooms Kaylin could have eaten using the second method is the sum of min(M[i], max_rate) for all intervals i, where M[i] is the number of mushrooms at the beginning of interval i and max_rate is the highest observable eat-rate. That is, if at the beginning of the interval the number of mushrooms is larger than the maximum eat-rate, Kaylin can only eat max_rate mushrooms, otherwise Kaylin can only eat M[i] mushrooms and the plate becomes empty until the end of that interval. Note that we don’t care about the number of mushrooms at the end of an interval. Since we want to minimize the eat-rate, we should assume that Bartholomew puts in mushrooms instantaneously at the end of the interval to maximize Kaylin’s idle time.
Below is a sample implementation in Python:
def first_method(M, N):
min_eat = 0
for i in range(1, N):
min_eat += max(0, M[i - 1] - M[i])
return min_eat
def second_method(M, N):
max_rate = 0
for i in range(1, N):
max_rate = max(max_rate, M[i - 1] - M[i])
min_eat = 0
# exclude the last mushroom
for i in range(0, N - 1):
min_eat += min(M[i], max_rate)
return min_eat
for tc in range(int(input())):
N = int(input())
M = map(int, raw_input().split())
print "Case #%d: %d %d" % (tc + 1,
first_method(M, N), second_method(M, N))
Analysis — B. Haircut
Direct simulation
Iterate over each minute, from the shop opening at time T = 0 until the last customer is served. At time T assign new customers to all available barbers (a barber is available if T is multiple of his M). Finally, report the barber who serves you.
public int naiveGetBarberNumber(int N) {
int customer = 1;
for (int T = 0; ; T++) {
for (int barber = 0; barber < B; barber++) {
if (T % M[barber] == 0) {
if (customer == N) return barber;
customer++;
}
}
}
}
This algorithm has time complexity O(N * max(M) * B), so it will be very slow, even for a small input, since N can be as large as 1,000,000,000.
Exploit periodicity
Consider the case where there are two barbers B1 and B2, who take 2 and 3 minutes respectively to cut a customer's hair.
| Time | Events |
| T = 0 | Both barbers are ready to serve customers. B1 serves customer #1 and B2 serves customer #2 |
| T = 2 | B1 serves customer #3 |
| T = 3 | B2 serves customer #4 |
| T = 4 | B1 serves customer #5 |
| T = 6 | Both barbers are ready to serve customers. B1 serves customer #6 and B2 serves customer #7 |
At T = 6, both barbers have become available, just as they were at T = 0. So we will see the same pattern of availability for the next 6 minutes as we did for the first 6 minutes — at T = 2 + 6, B1 will serve customer #(3+5); at T = 3 + 6, B2 will serve customer #(4+5), and so on until T = 6 + 6, at which point the process starts repeating itself again.
What's so special about 6? It's the least common multiple (LCM) of M1 = 2 and M2 = 3. At time T = LCM(M1, M2) = 6 each barber is available, because T % M = 0 for every barber. We can compute the LCM of all Ms as follows: LCM(M1, M2, M3, ...) = LCM(M1, LCM(M2, M3, M4, …)) and the least common multiple of two numbers is LCM(A, B) = A * B / GCD(A, B).
We can exploit the fact that the whole process is periodic and only simulate for a small number of customers. For example, say M1 = 2, M2 = 3, and you are N = 14th in line. We already know that we have a period of LCM(2, 3) = 6. During one phase B1 serves LCM(2, 3) / M1 = 3 customers and B2 serves LCM(2, 3) / M2 = 2 customers, i.e. in total 5 customers per phase are served in the shop. Since N = 14, you will be served in the 3rd phase. When the third phase starts you are going to be 4th in line, because a total of 10 customers have been served in the previous two phases. Finally, to figure out your barber's number, we can naively simulate your phase, similar to what we did in the first solution.
Since we are only simulating a single phase, we only really need to simulate at most LCM(M1, M2, M3, …) minutes. So our improved algorithm has time complexity O(B * LCM(M1, M2, M3, …)). Note that the LCM of all Ms is not going to exceed max(M)^B, i.e. LCM of all Ms is less than 25^5 for the small input.
public int slowGetBarberNumber(int N) {
int period = M[0];
for (int i = 1; i < B; i++)
period = period / gcd(period, M[i]) * M[i];
int customers_per_phase = 0;
for (int i = 0; i < B; i++)
customers_per_phase += period / M[i];
int N_in_my_phase = N % customers_per_phase;
return naiveGetBarberNumber(N_in_my_phase != 0
? N_in_my_phase : customers_per_phase);
}
For the large input, B and Ms can be as high as 10,000, so the LCM of them can get very large, and this approach will not work.
Binary Search
For a given time T, it is easy to compute the number of customers who have been assigned to a barber up to and including at time T. The number of customers who have been assigned to barber i is T/M_i + 1 (rounded down), so we can just sum these values for all the barbers.
public int countServedCustomers(long T) {
if (T < 0) return 0;
int served_customers = 0;
for (int barber = 0; barber < B; barber++)
served_customers += T / M[barber] + 1;
return served_customers;
}
This means we can use a binary search to figure out the time T when you are going to be served. After that, all you are left to do is figure out which of the available barbers at time T is going to serve you.
Keep in mind that at time T multiple barbers may become available, so you have to account for the customers that are ahead of you in line and are going to be served at the same time. Since you know that you will be served at time T, the number of potential customers ahead of you that are going to be served at time T is less than the number of available barbers. We can then simulate that, given that we know the number of customers that are going to be served up to and including time T-1. More precisely, the number of customers to be seated in the barber chair at time T is equal to countServedCustomer(T) - countServedCustomers(T-1).
What should the bounds for the binary search be?
For the upper bound, imagine a worst-case scenario: every customer ahead of you is served by the slowest and the only available barber. Meaning you are guaranteed to be served after max(M)*N minutes. For the lower bound, in the best case you are going to be served at the time the shop opens.
The implementation below assumes that you always will have been served at T = high or earlier, while at T = low you have not been served yet. So initially we want low to be -1, not 0.
The final complexity of this solution is O(B * log(N * max(M))).
public int fastGetBarberNumber(int N) {
long low = -1, high = 10000L*N;
while (low + 1 < high) {
long mid = (low + high) / 2;
if (countServedCustomers(mid) < N)
low = mid;
else
high = mid;
}
long T = high;
int customers_served_before =
countServedCustomers(T - 1);
int customers_to_be_served =
N - customers_served_before;
for (int barber = 0; barber < B; barber++)
// Is the barber available at time T?
if (T % M[barber] == 0) {
customers_to_be_served--;
if (customers_to_be_served == 0)
return barber;
}
}
Analysis — C. Logging
If there is only one tree in the forest, then obviously there is no need to cut anything down, and the answer for that tree is zero.
Otherwise, let's assume we have cut down some trees so that a given point P is on the boundary. If we follow the boundary clockwise from P, we will reach another boundary point Q. Imagine we are standing at P and looking along the boundary line towards Q. There can be no trees still standing to the left of this line, otherwise this would not be the boundary.
This suggests an algorithm for determining the minimum number of trees to cut down — for each point P, try each other point as a candidate for the next point around the boundary, Q; then check how many points lie on the left of the line PQ. The size of the smallest of those sets of points is the best answer:
For each point P
Let M = N-1
For each point Q ≠ P
Let Temp = 0
For each point R ≠ P, Q
If R is to the left of the line PQ
Temp = Temp + 1
If Temp < M
M = Temp
Output M
Cutting down all the trees to the left of PQ for some Q is sufficient to produce a valid solution, because no matter where the remaining trees are, P will be on the boundary. We can also be sure that this method will find the minimal solution, since whatever the minimal solution is, it will have some point Q which is the next along the boundary, and we have cut down the minimal number of trees to make that so.
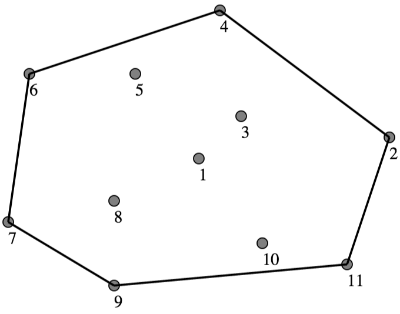
Figure 1
Consider the case in figure 1. Point #4 is already on the boundary, with Q equal to point #2, and we can see that there are no points to the left of the line PQ that we need to cut down, so the answer for point #4 is 0.
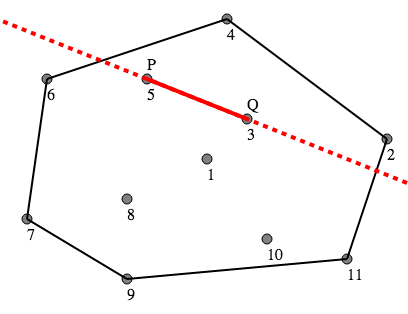
Figure 2
However, if P is point #5, then P is not already on the boundary. When we choose Q to be point #3, as in Figure 2, we find that there are two points to the left of the line PQ: point #2 and point #4. Cutting down those two trees will put P on the boundary.
However, this is not the minimal solution — when we try point #2 for Q, we will find a better solution, since only point #4 will need to be cut down.
This algorithm takes time O(N^3). But we can do better than this.
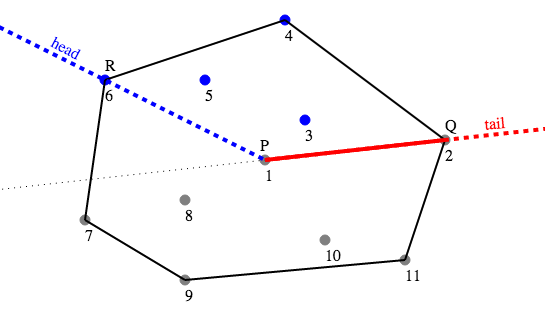
Figure 3
For each new point P, build an array S containing all the other points. Sort S by the angle of the line from P to that point. Now, we can try each possible point Q ≠ P by iterating through S, which gives an ordering of the points which moves counter-clockwise around P.
The advantage of this method is that for any choice of Q, all the points which lie to the left of the line PQ will occur after Q in the list S. So we can represent our current choice of Q and the set of points which lie to the left of PQ together as a "window" of points, implemented as two pointers into S — a "tail" pointer which points to Q, and a "head" pointer which points to the last point after Q which lies to the left of PQ. We call this point R in the diagrams.
In figure 3, we can see the state of this window for P = #1, Q = #2, R = #6. The tail of the window (in red) is at point #2, and the head of the window (in blue) is at point #6. The points #3, #4, #5, #6 are the ones which are to the left of PQ, so this choice of Q gives us a candidate solution which requires 4 trees to be cut down.
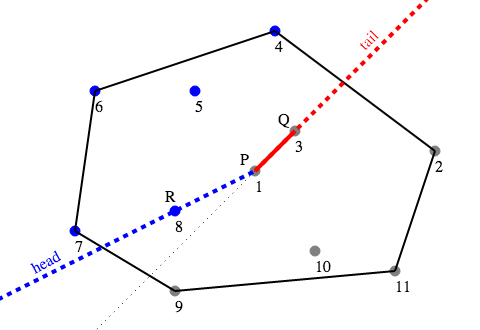
Figure 4
To update the position of the window for the next choice of Q, we need to do two things — move the tail ahead one point to the new choice of Q, and scan forward from the current position of the head pointer to find the new choice for R. In Figure 4, we can see that the tail has moved to point #3, and the head has moved to point #8. We now have a candidate solution which requires cutting down 5 trees (#4, #5, #6, #7, #8).
Since the tail of the window iterates through each point once, and the head of the window iterates through each point at most twice, this part of the algorithm takes O(N) time for each choice of P.
Sorting the points takes O(N log N) time for each choice of P, so in total this solution takes O(N^2 log N) time.
There are a few things to be careful of when implementing this algorithm:
- The head of the window will reach the end of S before the tail does. The head pointer then needs to wrap around to the start of S again, to include all the points to the left of PQ. For example, when Q = #6, the head of the window is #11. Then when Q advances to #7, the head of the window needs to wrap around to #2, which is at the start of the list, because point #2 is to the left of the line PQ.
- There may be no points to the left of PQ at all; for example, if P=#4, and Q=#2. A simple way to deal with this case is to have the head of the window equal to the tail. The calculation of the number of trees to cut down should naturally give zero. Then, when we advance the tail of the window by one point, also advance the head if it was at the same point.
- There may be more than one point at the same angle from P. This case is handled automatically. The points that are at the same angle will occur consecutively in S. When we choose the last such point as Q, we will correctly calculate the number of trees that need to be cut down. For the other points at the same angle, we will mistakenly think that extra trees need to be cut down, but we will still find the minimum, so we needn't write extra code to handle this case.
- When updating the position of the head of the window, we need to stop when the next point will be at an angle π or more greater than the angle of Q. Floating point numbers are imprecise, so we need to use an epsilon when doing comparisons in these calculations. The largest difference in angle between two points is approximately 1.25 * 10-13 radians. 64-bit floating point values have easily enough precision to represent angles with this difference, so using these with an epsilon of 10-13 will work.
Burunduk1, who won round 1A and had the fastest time for this problem, used an implementation of this algorithm.