Google Code Jam Archive — Round 3 2014 problems

There is an array of devices, each containing a known number of transistors, and among these there is 1 golden transistor both players want. Player 1 (Arnar) specifies a section of the array (this will divide the array into 3 sections [0,i), [i,j], (j,N-1]), then player 2 (Solveig) will pick one of the sections to take, leaving the other two for player 1. The problem asks us to find Arnar's chances of getting the special transistor given that both players act optimally and that every transistor has the same probability of being the golden one.

First, we recognize that we can compute the summation of any section of the array in O(1) time after precomputing a sum array. A sum array can be constructed using the following recurrence from 0 to N:

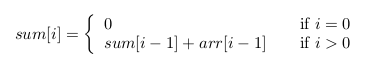
Then, for any partition of the device array, we can efficiently find the number of transistors inside each section using:

In order to determine the best boundaries that Arnar can put on the array, we can iterate through all the possible boundaries and store the best one. In code, this translates to using 2 for loops that cover all combinations of i and j with i <= j. For each, we can obtain the number of transistors in each resulting section (using the sum array as discussed above). Then, since Solveig will always take the section with the most transistors, Arnar’s score for a particular choice of boundaries is the minimum of any combination of 2 sections (right + left, middle + left, middle + right).

This solution runs in O(N^2) because we consider all combinations of i and j. This is good enough to pass the small input; however, it will timeout when running the large input. To pass the large input, we should come up with an O(N log N) algorithm. We need a couple more key observations for the O(N log N) algorithm:

First, notice that we can reformulate this problem as finding which 3-way partitioning minimizes the largest value of any partition, since Solveig will definitely choose the section with the most transistors after Arnar has decided on the 3-way partition.

Second, as a follow-up to the observation above, it only makes sense for Arnar to choose boundaries in which the values of the 3 sections are as close as possible with each other (otherwise Solveig will gain the upper hand by choosing the section that has significantly more transistors than the other 2, leaving less for Arnar).

The last insight that will allow us to come up with an O(N log N) algorithm is that the cumulative sum array is by nature sorted therefore it is monotonically increasing, which hints at the idea that we can utilize binary search. The algorithm idea is to iterate through the possible values for i (left boundary), and then to binary search for the optimal j (right boundary) given that left boundary. Specifically, we want the value of j that minimizes the difference between the transistor counts in the [i,j] section and the (j,N-1] section. We now describe the binary search process. We will start with 2 pointers (the possible range that our right boundary could be). The pivot will be in the middle of the 2 pointers (this is our guess at where the right boundary will be). If the right side of the pivot is greater than the left side of the pivot then we know our right boundary will be somewhere on the right and vice versa, so we can cut our possible range by half (and do so repeatedly until there is only one possibility).

Let’s go through an example for clarification. This example is taken from sample input 2 :

INPUT: 10 17 1 7 1  generates  [2 5 1 4 7 3 6 2 5 1]

Now let’s say our left pointer is between index 0 and 1 and we are trying to find the best right boundary using binary search. Our first guess should be for the right boundary to be between the left boundary and the end of the array (which puts it between values 3 and 6). The table below will illustrate the progression of our binary search. The first column contains a visualization of our array and the boundaries we are checking. The next 3 columns contain the values of each partition that is made by the boundaries. The last 2 columns tells us how many transistors each player will receive with the given partition. Each row is an iteration of our binary search.

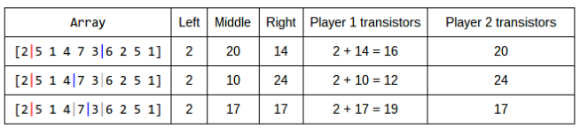
Notice that the right partition is always moving in such a way to maximize the value of the partition (middle and right) that is lacking (i.e. in the second row in the figure above we moved to the left because the middle partition value is greater than the right partition value in the first row).

Since we have a way to find the optimal partitioning with a given left boundary, our answer is then the best answer out of those after we iterate through all possible left boundaries. Binary search takes O(log N) and we do that for N left boundaries which gives us a total of O(N log N) runtime.

This solution is good enough to pass all of our tests; however, it is possible to do even better. For example, we can try to find a tight lower bound on Solveig's score by answering questions of the form: "Can Arnar produce a 3-way partitioning that limits Solveig to a score of at most Z?". Clearly there is some value K such that the answer to this question is "no" for Z < K and "yes" for Z >= K, which means that K can be found by binary search.

In order to answer such a question, we note that given Z, Arnar can't do better than to choose the left and middle sections greedily: he selects i as large as possible while putting no more than Z transistors in the left section, and then j as large as possible while putting no more than Z transistors in the middle section. Then, if the resulting right section also contains no more than Z transistors, the answer to the question is "yes", otherwise "no". Finally, we see that these values for i and j can be found efficiently by using binary search in the sum array, so we can answer our question for a specific Z in O(log N) time.

This strategy takes O((log N)^2) for the outer binary search (we ask O(log N) questions that each take O(log N) time to answer), but of course it also requires use of the sum array which takes O(N) time to compute. Therefore, the overall complexity is O(N). Perhaps surprisingly, it is even possible to solve this problem in O((log r)(log N)^2)! See if you can figure out how to use some complicated math to avoid computing all O(N) elements of the sum array (hint: you need to exploit the particular formula given for the number of transistors in each device).

Diana and the tower take turns in shooting N monsters and Diana goes first. Diana can shoot any monster or skip the turn, while the tower always shoots the monster that is the closest to the tower. Each monster i starts with a certain hit points H_i and it decreases by P when shot by Diana and decreases by Q when shot by the tower. If the hit points goes below 1, the monster dies and cannot be shot further. Diana is awarded G_i gold if her shot kills the i-th monster, but none if the tower’s shot kills it. What is the maximum amount of gold Diana can obtain?

The key observation here is that, for Diana, shooting a monster other than the one currently targeted by the tower is exactly equivalent to not shooting any monster in this turn and instead getting an “extra” shot that can be used at a later turn. Later, Diana may use some or all of her accumulated extra shots consecutively. So instead of making the decision “which monster do I shoot?” before each tower shot, Diana only needs to decide whether to use one of her extra shots (on the closest living monster) or let the tower take a shot.

This reduces the problem to a dynamic programming (DP) solution with the state being: the current monster i to target, the remaining hits points for the current monster and the number extra shots that Diana has. Note that since there is a lower limit on P and Q, the maximum number of extra shots for Diana is 1000. In the DP solution, there are three transitions:

1. The current monster is dead and we move on to the next monster,
2. Diana skips a shot and gains one extra shot (letting the tower shoot once),
3. Diana shoots the monster once using her extra shots, possibly killing the current monster and getting its gold.

Below is the pseudocode for the top-down dynamic programming with some clarifying comments:

# We are at monster i which has rem_hp HP left and Diana has
# extra_shots shots saved up, how much gold can she get?
function rec(i, rem_hp, extra_shots)
  # Base case: all monsters have been killed.
  if (rem_hp <= 0 && i + 1 == N) return 0

  # Monster i is dead, move on to the next one.
  if (rem_hp <= 0) return rec(i + 1, H[i + 1], extra_shots)

  # Memoization.
  if is_set(memo[i][rem_hp][extra_shots])
    return memo[i][rem_hp][extra_shots]

  # The tower shoots next. Diana saves up another shot.
  ret = rec(i, rem_hp - Q, extra_shots + 1)

  # Diana shoots next, using one of the saved up shots.
  # If the shot kills the current monster, she gets its gold.
  if (extra_shots > 0)
    gold = (rem_hp <= P) ? G[i] : 0
    ret = max(ret, gold + rec(i, rem_hp - P, extra_shots - 1))

  return memo[i][rem_hp][extra_shots] = ret


# Since Diana plays first, she has one extra shot initially.
print rec(0, H[0], 1)

You are given a log of criminals entering and leaving a house from the front door. The log is for one day, and at the start of the day there might be criminals in the house. This house may have other entrances and exits besides the front door, and the criminals might wear masks when entering/leaving the house. The task is to figure out if, given the log, it is possible that there is only one door (i.e. the front door only), and if so to figure out the minimum number of people that could be in the house at the end of the day.

Building intuition:

Before proceeding with the solution, let us develop some intuition for the problem. Let us say we are actually given a log where none of the criminals wore a mask, i.e. none of the entries are ‘E 0’ or ‘L 0’. In that case, the solution would be to simulate the log from start to end, i.e. simulate criminals entering and leaving the house via one door only, and to see if the simulation is valid. When is a simulation valid? Let us instead discuss when a simulation would be invalid. During the simulation, if we encounter a ‘E X’ command (note X > 0), and ‘X’ was already in the house then it is invalid (impossible to enter twice without leaving). Similarly if we encounter a ‘L X’ command, and ‘X’ isn’t already in the house then it is invalid. Note that if it was the first time encountering the ‘L X’ command then we can say that ‘X’ was already in the house at the start of the day so it would be valid.

The reason why the problem we are given is complicated is because of the presence of masked criminals. We are going to tackle this problem using a greedy strategy. We will first assume that there are ‘S’ number of criminals at the start of the day. Then we will do a simulation like we described before (i.e. simulation from start to end), except whenever we encounter a masked criminal, we will try to greedily assign a criminal number to the masked criminal. We will describe this greedy assignment later, but first let us describe a few terms we use in the editorial.

Terms:

Let us first describe some of the terms we use in this editorial. We call the log an event queue, which is a sequence of ‘E 0’, ‘L 0’, ‘E X’, or ‘L X’ (where X > 0) events. During our simulation, we will go through the queue from start to end. During the simulation let us say we are at index i in the event queue, then we define the current event queue to be the subsequence of the event queue starting from index i to the end of the queue. During the simulation, we will also maintain a set of criminal numbers that are inside the house: we call the set INSIDE. Finally, the last term to define is the next known event for a particular criminal (non-zero) number. To help understand this term, we will use an example. Let us say our current event queue (along with the location indices) is:

0: ‘E 0’
1: ‘E 0’
2: ‘E 5’
3: ‘L 1’
4: ‘E 1’
5: ‘L 1’
6: ‘E 1’
7: ‘L 5’
8: ‘E 2’

There are three unmasked criminal numbers: 1, 2 and 5. Note we do not consider the masked criminals. Criminal ‘1’ appears 4 times in the current queue at indices 3, 4, 5, and 6. The next known event for criminal ‘1’ is defined to be ‘L 1’ at index 3 (which is the earliest among the 4 events). Similarly criminal ‘2’ appears 1 time at index 8, therefore the next known event for criminal ‘2’ is ‘E 2’ at index 8. Similarly criminal ‘5’ appears 2 times, at indices 2 and 7. The next known event for criminal ‘5’ is defined to be ‘E 5’ at index 2.

Greedy strategy:

Now, let us proceed with the explanation for the greedy solution. First, let us assume we start with ‘S’ criminals already in the house. We will simulate the presence of these ‘S’ criminals in the house by adding ‘S’ ‘E 0’ events at the start of the event queue. To make things simpler during the simulation, we will pretend that all the criminals leave at the end of the day. To do so, we can add ‘T’ ‘L 0’ events to the end of the event queue such that the number of ‘E’ events and ‘L’ events are equal. We will then proceed to simulate this resulting event queue to check for validity and also in the process, if possible, assign numbers to the masked criminals. If the simulation is a valid simulation then for this event queue, our answer is ‘T’ i.e. the number of criminals remaining in the house at the end of the day. We will discuss how we find ‘S’ (and correspondingly ‘T’) later.

We now describe the simulation. As mentioned earlier, we simulate from the start to the end. If we are able to successfully go through all the events then this event queue is a valid event queue. At any instant we have a current event queue (which is defined above). Note that at the start of the simulation, the set INSIDE is an empty set. We will now discuss how to address the four cases for the first event in the current queue, i.e. the cases ‘E X’, ‘L X’, ‘E 0’ and ‘L 0’ (note that X > 0).

Case ‘E X’:

In this case, person ‘X’ is entering the house. It will only be valid if ‘X’ is not already inside the house, which we can check by seeing if the INSIDE set does not already contain ‘X’. If true, then this is a valid event, else it is an invalid event hence an invalid simulation therefore we end the simulation. Also, if ‘E X’ is valid, we need to update the INSIDE set by adding ‘X’ to it.

Case ‘L X’:

In this case, person ‘X’ is leaving the house. It will only be valid if ‘X’ is already inside the house, which we can check by seeing if the INSIDE set contains ‘X’. If true, then this is a valid event, else it is an invalid event hence an invalid simulation therefore we end the simulation. Also, if ‘L X’ is valid, we need to update the INSIDE set by removing ‘X’ from it.

Case ‘E 0’:

In this case, a masked criminal is entering. Our objective is to assign a number to this masked criminal. If we are able to assign a number to the masked criminal, the criminal will then enter the house which we do so by adding the assigned criminal number to the INSIDE set. Now the question is how do we assign numbers to this masked criminal. There are two cases to consider:

Case ‘E 0’ (a):

First, we consider the set of known criminals (i.e. ones that aren’t masked) in the current queue who are also not inside the house (i.e. not in the INSIDE set). Out of these criminals, we consider the criminals for which the next known event is a leave event (i.e. ‘L X’ for criminal ‘X’). These are the people who need to leave the house at some point, but it isn’t known when they leave the house. All of these people must enter the house in ‘E 0’ events that happen before they leave. If such a person exists, we make a greedy choice and choose the person who is leaving soonest, to leave ourselves with maximum time to get the remaining people out. Why do we make this greedy choice? Consider two such people, 1 and 2. The sequence, then, looks like this:

‘E 0’ ... ‘L 1’ ... ‘L 2’

Note that the ‘...’ denotes other events in the event queue which we do not list out to avoid complexity. In order for this event queue to be valid, there must be another ‘E 0’ to match the ‘L 1’ and ‘L 2’ events (note that 1 and 2 are not in the INSIDE set). There are two possibilities then:

‘E 0’ ... ‘E 0’ ... ‘L 1’ ... ‘L 2’

‘E 0’ ... ‘L 1’ ... ‘E 0’ ... ‘L 2’

In both situations, choosing the entering masked criminal to have been criminal number ‘1’ works. But if we had instead chosen the entering masked criminal to have been criminal number ‘2’, then the second possibility listed above would be invalid (the second ‘L 1’ cannot be matched with the ‘E 0’ that comes after it). Therefore we are better off if we choose ‘1’. This logic generalizes to the case where there are more than two people.

Case ‘E 0’ (b):

If no such person in Case ‘E 0’ (a) exists, we simply create a new person who doesn't show up anywhere unmasked (i.e. assign a number that is big e.g. a million; make sure to assign unique numbers to each new person). Why create a new person? It is because the alternative is to use someone who is outside the building, but whose next known event is an enter event. For example, let's suppose the person doing that is person 5. Then we have a sequence like this:

‘E 0’ ... ‘E 5’

For person 5 to be entering at the start, we need the sequence to look like this:

‘E 0’ ... ‘L 0’ ... ‘E 5’

In that situation, having person 1,000,000 enter is just as good as having person 5 enter. But in the situation where there is no ‘L 0’ between the ‘E 0’ and the ‘E 5’, person 1,000,000 could leave the house later (if there is a ‘L 0’ afterwards), but person 5 is stuck entering the house, then entering it again causing the simulation to be invalid. Therefore we better off to create a new person with a new unique number in such cases.

Case ‘L 0’:

In this case, a masked criminal is leaving the house. As in the case for case ‘E 0’, the goal is to assign a number to the masked criminal. After assigning the number ‘X’ to the criminal (if that is possible), we must update the INSIDE set by removing ‘X’ from the set. Note that if the INSIDE set is empty when we encounter the ‘L 0’ event then it is an invalid simulation. For cases when there are criminals in the INSIDE set, there are three cases to consider:

Case ‘L 0’ (a):

Consider all the criminals who are inside, and whose next known event is that they are entering the house. By the same logic as in Case ‘E 0’ (a), we choose the one who is entering the soonest. If we are able to do such an assignment, we need not consider any of the other ‘L 0’ cases.

Case ‘L 0’ (b):

If no such person in the previous case exists, then we consider all criminals who are inside the house. If there is one criminal who has no next known event (either ‘E X’ or ‘L X’) with the house, have that person leave; they have to leave at some point in no particular order, and it's better to have them leave than someone whose next known event is that they are leaving. If we were able to choose such a criminal, then we need not consider the last case.

Case ‘L 0’ (c):

If no such person in the previous two cases exists, we're now stuck with criminals who are inside and whose next known event is that they're leaving. In such a case, we make a greedy choice and take the one who leaves as late as possible, so we have the maximum number of chances for our selected person to enter the house again (with an ‘E 0’ event). Why do we make this greedy choice? Consider two such people we need to choose from, 1 and 2. The sequence, then, looks like this:

‘L 0’ ... ‘L 1’ ... ‘L 2’

In order for this to be valid, there must be another ‘E 0’. There are two possibilities:

‘L 0’ ... ‘E 0’ ... ‘L 1’ ... ‘L 2’

and

‘L 0’ ... ‘L 1’ ... ‘E 0’ ... ‘L 2’

In both situations, assigning the leaving masked person (‘L 0’) to be person 2 works, but choosing 1 does not work for the second possibility. So we are better off to choose person 2 for ‘L 0’. This logic generalizes to the case where there are more than two people.

And so that concludes the four cases to consider for the first event in the current queue. As discussed earlier, if the first event is deemed invalid when considering the four cases, then we have an invalid simulation. But if we are able to successfully assign a criminal number, then we advance to the next event in the event queue and get a new current queue, and continue on with our simulation. If we reach the end, then it is a valid event queue.

Picking ‘S’ criminals initially in the house:

Earlier on, we had assumed there were ‘S’ criminals initially in the house. But the question is what value do we consider for ‘S’? We can try all values from 0 to N (the size of the queue). Doing so one by one might still be slow for the large input. However, we can use binary search to make the search faster. Note that having more people (larger ‘S’) in the house gives us more flexibility to make the simulation work i.e. bigger values of ‘S’ gives us more ‘E 0’ at the start and more ‘L 0’ at the end to work with. Also if the simulation was valid for ‘S’ = i, it would be valid for ‘S’ = i + 1 too because we are adding a ‘E 0’ at the start and correspondingly a ‘L 0’ at the end (which can match each other in our already valid simulation for ‘S’ = i). This means that for the smaller values of ‘S’, we might get invalid simulations (i.e. false values), but after a certain ‘S’ value we will start getting valid simulations (i.e. true values). This indicates that the boolean function (i.e. that function that indicates whether the simulation is valid or not) is a monotonic boolean function (for input ‘S’ = 0 to N). When a function is monotonic, we can use binary search to make the search faster.

Finally, as specified in the problem, if we are unable to find any valid simulation for any of the values of ‘S’ then we report “CRIME TIME” as the answer.

The problem can be paraphrased as follows: we are given a tree with N vertices where each vertex i has Ci coins. There are two players taking turns in the game. First, each player picks a starting vertex (could be the same vertex), then player 1 makes the first move. In a move, the player picks a new neighboring vertex adjacent to the last picked vertex, forming a simple path. The path of one player is allowed to intersect with at most one vertex (i.e., no edges overlap) with the path of the other player. The game ends when neither player can make a move. The score for the player is the sum of all coins in the vertices picked by the player subtracted by the sum of all coins in the vertices picked by the other player. Our task is to find the maximum score player 1 can get.

There are N possible starting vertices for player 1. After player 1 picks a starting vertex, player 2 also has N possible starting vertices. Both players will pick a starting vertex that maximizes their score. The high level solution for finding the maximum score for player 1 is shown in the pseudocode below:

  p1_max_score = -INFINITE
  for p1_start_vertex in 1 .. N:
    min_score = INFINITE
    for p2_start_vertex in 1 .. N:
      p1_score = minimax(p1_start_vertex, p2_start_vertex)
      min_score = min(min_score, p1_score)
    p1_max_score = max(p1_max_score, min_score)

  print p1_max_score

Player 1 tries to pick the starting vertex that maximizes the p1_max_score while player 2 tries to pick the starting vertex that minimizes player 1’s score. The function minimax is the main algorithm to maximize the score for the first player, given the starting vertex of each player.

In the next two sections, we will present two minimax algorithms. The first minimax algorithm is based on a depth-first search simulation which runs in O(N^2), thus giving the overall complexity of O(N^4). The other minimax algorithm is based on dynamic programming which can be precomputed in O(N^2) and gives answers in O(1), thus giving the overall complexity of O(N^2 + N^2) = O(N^2).

Minimax using simulation O(N^2)

Given the starting vertex for each player, we can do a depth-first search (DFS) simulation for the minimax algorithm. The DFS state is the last vertices picked by each player and the player currently making the turn. The current player that makes the turn first grabs the coins at the current vertex and then tries to pick a neighboring vertex to visit that maximizes the total coins. Before visiting the neighboring vertex, the (bi-directional) edge connected to the new vertex is removed and later restored when the DFS backtracks. Finally, if the current player cannot make a move, then the player gives the turn to the other player to continue to make a move. The pseudocode below shows the sketch of the algorithm.

function rec(i, j, turn)  # See note 1
  if visited[i][j][turn] return 0  # See note 2
  visited[i][j][turn] = true

  ci = C[i]  # See note 3
  C[i] = 0  # Remove the coins at vertex i

  ret = -INF
  for each neighbor ni of i
    remove edge[i][ni]  # See note 4
    ret = max(ret, -rec(j, ni, 1 - turn))
    restore edge[i][ni]

  if ret == -INF
    ret = -rec(j, i, 1 - turn)  # See note 5

  C[i] = ci  # Restore the coins at vertex i

  return ret + ci

Notes:

1. The first parameter i of the rec function is the last vertex picked by the current player that is currently making the turn. The second parameter j is the last vertex picked by the other player. The third parameter turn is the player ID that is making the turn (0 is the first player and 1 is the second player)
2. The state (i, j, turn) is visited exactly once. The next visit to this vertex returns 0 which signifies a terminal condition.
3. We temporarily store the coins at the vertex of the current player. Then we remove coins from the vertex i (so that further moves in the DFS cannot reuse the coins again), and later restore the coins before returning.
4. Removing the connecting edge before visiting (recursing) the next vertex ensures that the edge will not be used any further by any of the players later in the DFS. Notice that the edge is restored later when the recursion backtracks. The same is true for the coins.
5. If the current player cannot move, it must give the turn to the other player.

Given the starting vertex of both players, the DFS simulation above runs in O(N^2) to compute the maximum score for the first player. This comes from the number of distinct states in the parameters (N^2) and the fact that we never process the same state twice. The inner loop which loops through the neighbors of i can be amortized to O(1) since on average each vertex has 1 outgoing edge.

Unfortunately, for different starting vertices, we cannot reuse the computation (i.e., we need to clear the visited states and start from scratch). Therefore the overall runtime complexity is O(N^4) which is only good for the small input N = 80.

Minimax with Dynamic Programming O(1)

The idea behind the O(1) runtime complexity is to be able to reuse the computation when computing for different starting vertices for each player. The DFS state described in the previous section is not independent from another DFS state because it has to keep track of the coins that have already been taken and also the edges that cannot be used anymore. Different DFS states have different sets of coins and edges that are available. If we can design a state where it does not need to care about which coins or edges are available, then we can make each state independent and we can memoize (cache) the state results and reuse it to compute other states. This way, each state can be computed in O(1).

To design a state that is independent of each other, we need to make an important observation: after a player makes a move, the edge connecting the last vertex to the new vertex is removed. If the new vertex is now unreachable from the other player’s last vertex then the two vertices are disconnected and each vertex is in its own tree, then the solution becomes trivial: each player simply takes the best path that remains open (the best path is the path that gives the maximum total coins) in its own tree. We therefore only need to perform minimax across states where the last vertices for both players are still in the same tree.

In our new minimax algorithm, the state space can be entirely described by the last edge traversed by each player (which is only O(N^2) pair of edges). There are two choices for the current player to move (i.e., to pick the new neighboring vertex):

1. Pick the vertex towards the other player’s last vertex. Note that the input graph is a tree, therefore, there is exactly one unique path connecting the last vertices of both player. The player picks the next vertex in this path that brings them closer together. This move will transition (recurse) to a new state where the other player is now the one taking the turn. The new state is independent from the previous state since we do not need to care about which coins or edges have been removed (i.e., the current player cannot go back to the previous vertex and the other player cannot reach the vertices behind the current player anyway). The vertex that leads to the other player’s last vertex can be found in O(1) by precomputing it beforehand. The precomputation uses dynamic programming where the states are the last edge used by the current player, and the last vertex of the other player. The transition for the current player is to move closer to the last vertex of the other player which can be done in O(1) since each vertex has 1 edge on average (please refer to the sample implementation below for the details of how the next_node_to is pre-calculated). Now, let’s see an example for the first choice we have just described:
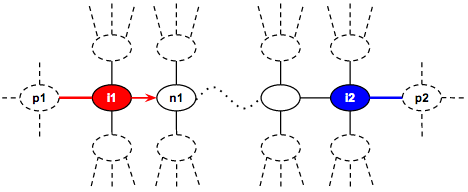
   Player 1 is the current player that is making the move and is at vertex i1 and the last edge used is the connecting edge to vertex p1. Player 2 is at vertex i2 and the last edge used is the connecting edge to vertex p2. The current player 1 makes a move by picking the vertex n1 that leads to i2 (there is exactly one path that leads to i2). After player 1 makes a move, we can recurse to a new independent state where the current player is player 2 at i2 with the same last edge and the other player is player 1 at n1 with the last edge being the connecting edge to i1.
   
   
2. Pick the next best vertex that does not lead to the other player’s last vertex. We can pick the vertex in O(1) if we precompute the list of next best vertex beforehand. This move will disconnect the current player’s newly picked vertex from the other player’s last vertex and their maximum total coins can now be processed independently in O(1) as explained in the example below. The other player can then independently pick the best path that avoids the edges used by the current player in O(1). We demonstrate it with the following example:
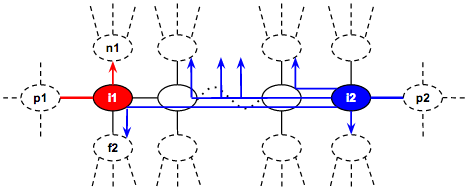
   Just like before, player 1 is the current player that is making the move and is at vertex i1 with the last edge connecting to vertex p1. The other player is player 2 at vertex i2 with the last edge connecting to vertex p2. The current player 1 picks the new vertex n1 which is the vertex leading to the best path that is disconnected with the other player’s last vertex i2. At this point, both players become independent. Player 2 is free to pick the best path that avoids the two edges used by player 1 (marked as red edges). Player 2 can try moving in the direction to i1 and then “branch-off” at any time to another direction to find its best path. The special case is when it has reached i1, it cannot branch-off in the direction of p1 nor n1 since those edges are already used. Player 2 can only branch-off to vertex f2 from vertex i1. This means that it is sufficient to keep the best 3 outgoing edges for each vertex because when we branch-off, we only consider the next best path to branch-off and the 3rd best path is used only in the special case. We can pre-compute the maximum total coins gained via branching-off in between i2 to i1 (both inclusive) using dynamic programming in O(N^2) (please refer to the branch_off_between method and its comments in the sample implementation below). Thus, to answer the maximum coins that player 2 can get in this case can be answered in O(1).

The two cases above can be answered in O(1), therefore each state can be computed in O(1) and the result can be cached and reused to compute other states (i.e., it does not need to be re-set for different starting vertices). Since there are O(N^2) possible last edges for each player, there are only O(N^2) distinct states. Therefore, given any two starting vertices for each player, the new minimax algorithm can answer the maximum score for player 1 in O(1).

Below is the sample implementation in C++11.

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <vector>

using namespace std;

#define MAXN 4001
#define MAXE (MAXN * 3)

vector<int> con[MAXN];
int T, N, C[MAXN], id;
int edge_id[MAXN][MAXN];
int next_node_to[MAXN][MAXN];
int best_coins[MAXE];
int best_nodes[MAXE][3];
int memo_rec[MAXE][MAXE];
int memo_branch_off[MAXE][MAXE];

// Pre-calculate the next_node_to, best_coins, best_nodes.
void precalc(int i, int pi, int from, int first_node) {
  next_node_to[from][i] = first_node;
  int &best = best_coins[edge_id[i][pi]];
  best = 0;
  vector<pair<int, int> > arr;
  for (int ni : con[i]) if (ni != pi) {
    precalc(ni, i, from, first_node);
    int coins = best_coins[edge_id[ni][i]];
    arr.push_back(make_pair(coins, ni));
    best = max(best, coins);
  }
  sort(arr.rbegin(), arr.rend());
  for (int j = 0; j < arr.size() && j < 3; j++)
    best_nodes[edge_id[i][pi]][j] = arr[j].second;
  best += C[i];
}

// Returns the best next vertex when coming from
// edge (pi -> i), excluding vertex v1 and v2.
int next_best_except(int i, int pi, int v1, int v2 = -1) {
  int ei = edge_id[i][pi];
  int j = 0, *arr = best_nodes[ei];
  if (arr[j] == v1 || arr[j] == v2) j++;
  if (arr[j] == v1 || arr[j] == v2) j++;
  return arr[j];
}

// Maximum coins for sub-tree i with parent pi.
int max_coins(int i, int pi) {
  return (i < 0) ? 0 : best_coins[edge_id[i][pi]];
}

// Maximum coins for branching off at any vertex in [i, j].
int branch_off_between(int i, int pi, int j, int pj) {
  int ei = edge_id[i][pi];
  int ej = edge_id[j][pj];
  int &ret = memo_branch_off[ei][ej];
  if (ret != -1) return ret;

  if (i == j) {
    int ni = next_best_except(i, pi, pj);
    int nj = next_best_except(i, pi, pj, ni);
    // The other player takes the third best vertex nj since
    // the best two are already taken by the current player.
    return ret = max_coins(nj, j);
  }

  int nj = next_node_to[j][i];
  int njb = next_best_except(j, pj, nj);
  int branch_off_now = max_coins(njb, j);
  int branch_off_later = ((nj == i) ? 0 : C[nj])
    + branch_off_between(i, pi, nj, j);

  return ret = max(branch_off_now, branch_off_later);
}

// Minimax for the current player with last edge (pi -> i)
// and the other player with last edge (pj -> j).
int rec(int i, int pi, int j, int pj) {
  int ei = edge_id[i][pi];
  int ej = edge_id[j][pj];
  int &ret = memo_rec[ei][ej];
  if (ret != -1) return ret;

  if (i == j) {
    // The current player pick the next best path.
    int ni = next_best_except(i, pi, pj);
    // The other player pick the next next best path.
    int nj = next_best_except(i, pi, pj, ni);
    return ret = max_coins(ni, i) - max_coins(nj, j);
  }

  // The first option for the current player:
  // The current player pick the vertex ni
  // that leads to other player last vertex.
  int ni = next_node_to[i][j];
  int option1 = ((ni == j) ? 0 : C[ni]) - rec(j, pj, ni, i);

  // The second option for the current player:
  // The current player go to the best path other than ni.
  ni = next_best_except(i, pi, ni);
  int p1coins = max_coins(ni, i);
  // The other player branch off at any point
  // between vertex i and j (inclusive).
  int p2coins = branch_off_between(i, pi, j, pj);
  int option2 = p1coins - p2coins;

  // Pick the best outcome for the current player.
  return ret = max(option1, option2);
}

int main() {
  scanf("%d", &T);
  for (int TC = 1; TC <= T; TC++) {
    scanf("%d", &N);
    for (int i = 0; i < N; i++) {
      scanf("%d", &C[i]);
      con[i].clear();
    }
    id = 0;
    memset(edge_id, -1, sizeof(edge_id));
    for (int i = 0, j; i < N - 1; i++) {
      scanf("%d", &j); j--;
      con[i].push_back(j);
      con[j].push_back(i);
      edge_id[i][j] = id++;
      edge_id[j][i] = id++;
    }
    for (int i = 0; i < N; i++) {
      edge_id[i][N] = id++;
    }

    // These memoizations are reset per test case.
    memset(best_coins, -1, sizeof(best_coins));
    memset(best_nodes, -1, sizeof(best_nodes));
    memset(next_node_to, -1, sizeof(next_node_to));
    memset(memo_rec, -1, sizeof(memo_rec));
    memset(memo_branch_off, -1, sizeof(memo_branch_off));

    // Pre-calculation.
    for (int i = 0; i < N; i++) {
      precalc(i, N, i, N);
      for (int j : con[i]) precalc(j, i, i, j);
    }

    int max_diff = -1000000000;
    for (int i = 0; i < N; i++) {
      int min_diff = 1000000000;
      for (int j = 0; j < N; j++) {
        int cost = C[i] - (i == j ? 0 : C[j]);
        min_diff = min(min_diff, cost + rec(i, N, j, N));
      }
      max_diff = max(max_diff, min_diff);
    }
    printf("Case #%d: %d\n", TC, max_diff);
  }
}