Google Code Jam Archive — Round 1B 2014 problems

Let us first examine the winning condition for Omar. For this we will consider the following example:

3
aabcaa
abbcaa
abccaa

We represent the given strings by borrowing an idea from Run-length Encoding. Using the idea from this encoding the string “aabcda” can be represented as “2:a, 1:b, 1:c, 1:d, 1:a”. The representation shows an ordered list of pairs of frequency and the corresponding character, let’s call it the frequency string. Similarly, we can figure out the frequency strings for all the original strings. The frequency strings for the strings in the example are listed below:

aabcaa  ->  2:a, 1:b, 1:c, 2:a
abbcaa  ->  1:a, 2:b, 1:c, 2:a
abccaa  ->  1:a, 1:b, 2:c, 2:a

So we know how to figure out if Omar can win or not, we are now interested in the minimum number of actions to win the game. Notice that the actions performed on the i^th character in the frequency strings can be applied independently from characters in other positions in the frequency strings. Thus, we can process a set of characters at position i before processing the characters in the next position. For the example above, we can solve the leading “a” first, then “b”, then “c”, and finally the trailing “a”. From hereon, we will describe solving for one character (at the i^th position) in the frequency strings. All other characters can be solved in the same way.

Brute force algorithm:

In the brute force solution, we will try all possible frequencies for a single character, that is for the character “a”, we will try all possible frequencies of “a” which are “1:a”, then “2:a”, then “3:a”, etc. We call each frequency we try the target frequency. In this problem, as the length of the string is only upto a 100 therefore we can try all possible frequencies from 1 through 100. For each target frequency, we can compute the sum of total actions (which will be the absolute difference between the frequency of that character and the target frequency) and maintain the target frequency that gives us the minimum sum of total actions.

The time complexity for the brute force algorithm is O(L*N*X), where L is the maximum length of any string, N is the number of strings, and X is the number of characters in the frequency string.

This solution should be sufficient to solve the provided small and large data set.

Efficient algorithm:

In the brute force solution, we tried all possible frequencies for a single character. But we don’t need to do so, we can just try only one target frequency!

We would like to point out that intuitively, one might think that the mean would be the target frequency. Let’s go through an example. Suppose we are given the frequencies {1, 1, 100}. The mean is 34. The sum of absolute differences from the provided frequencies to the target frequency is 33 + 33 + 66 = 132. But what if the target frequency was 30 instead of 34? Then the sum of absolute differences is 128, which is less than 132! In fact, if we tried all possible values for the target frequency (from 1 through 100), we would find that the minimum is at 1 with a sum of 99. In fact, it is the median that minimizes sum of absolute differences (1 is the median of {1, 1, 100}).

In our example above, the frequencies for leading “a” are {2, 1, 1}, for “b” are {1, 2, 1}, for “c” are {1, 1, 2}, and for trailing “a” are {2, 2, 2}. Therefore for the leading “a”, we would use the median which is 1 as the target frequency. Similarly for “b” and “c” we use 1, while for the trailing “a” the target frequency is 2.

You might be wondering why the median is the right target frequency, we refer to an excellent explanation by Michal Forišek to the question “Why does the median minimize the sum of absolute deviations?” which we quote here:

Imagine the given values as trees along a road. The quantity you are trying to minimize is the sum of distances between you and each of the trees.

Suppose that you are standing at the median, and you know the current value of the sum. How will it change if you move in either direction? Note that regardless of which direction you choose, in each moment you will be moving away from at least half of the trees, and towards at most half of the trees. Therefore, the sum of distances can never decrease -- and that means the sum of distances at the beginning had to be optimal.

In the explanation above, minimizing the sum of absolute deviations is equivalent to minimizing the total actions required to convert any i^th character in the frequency string to a target frequency in our problem.

In this problem, we are given three positive integers A, B and K. We are asked to calculate the number of pairs of integers (a, b) such that:

1. 0 ≤ a < A
2. 0 ≤ b < B
3. (a AND b) < K (denote AND means bitwise-AND of a and b).

Solving the small dataset

For the small dataset, we can simply enumerate all pairs (a, b) that meet the first two constraints and count how many match the third constraint. Most programming languages have the built-in bitwise-AND operation, usually as the character “&”. This procedure will have a time complexity of O(AB), which is sufficient for the small dataset. Following is a sample implementation in Python 3:

def f(A, B, K):
  return len([(a, b) for a in range(A) for b in range(B) if (a & b) < K])

Solving the large dataset

We present two approaches for solving the large dataset in this problem. The first one is a standard Dynamic Programming solution (DP on digits/bits) that can be applied to different problems which are of a similar flavor. The second approach divides the search space into different sets, and computes the size of each set recursively.

First approach

Before delving into the actual solution, let us start thinking about a simpler problem: given an integer M, write a recursive function to count all non-negative integers m where 0 ≤ m < M. The answer is trivially M, but bear with us as our intent for this simpler problem is to build an intuition for the Dynamic Programming (DP) function which will be similar to the DP function we will write for the actual problem.

The core idea is based on counting the number of ways to generate the bits for the number m, such that they are always less than or equal to M but then we only count those that are strictly less than m. We can start by generating the bits of m from the most significant bit to the least significant bit, and for each bit position, generating only the feasible values. Note that the feasible values for the i-th bit can sometimes be both 0 and 1, or only 0.

Let’s say M is 29 (which is 11101₂ in binary). The most significant bit is the bit at the fourth position and the least significant bit is at the zeroth position as shown here:

11101 (M = 29)
^^^^^
|||||
43210 (bit positions 4, 3, 2, 1, 0)

We will refer to the i-th bit as m_i. Let’s say we have generated value 1 for m₄, value 0 for m₃, and we want to generate the feasible values for the bit at position i = 2. We can represent our current state as: 10cyy, where 1 and 0 are the values we have chosen, ‘c’ is the current (i-th) bit we want to generate and ‘y’ denotes the bits we will try to generate in the future. We call the bits to the left of position i as prefix. The prefix for the partially generated m_i = 10cyy is 10 (where i = 2). Now we explain the rules which help us decide the feasible values to use for the i-th bit c:

• Rule 1: we can always use value 0 for bit at position i.
• We can use value 1 for bit at position i if either:
  • Rule 2a: The prefix of the bits before position i in m (which is already generated) is less than the prefix of the bits before position i in M, or
  • Rule 2b: The i-th bit of M is 1.

1. Let’s say our current state is m = 10cyy as before. We want to determine candidate values for ‘c’. In this case, the prefix is 10, and M’s prefix is 11 therefore both values 0 and 1 are feasible. Value 0 is always feasible (Rule 1) while from Rule 2a, value 1 is feasible.
2. If our current state is m = 11cyy, then both values 0 and 1 are feasible since value 0 is always feasible (Rule 1) while from Rule 2b, value 1 is feasible.
3. If our current state is m = 111cy, then only value 0 is feasible (Rule 1) but value 1 is not feasible since neither Rule 2a nor Rule 2b can be satisfied.

Note that as soon as the current prefix of m before position i is less than the prefix of M before position i, we can use both values 0 and 1 for the rest of the bit positions from i down to 0. Remember that we generate the bits from the most significant bit to the lowest (i.e., decreasing i).

We now proceed with describing the implementation. We define a recursive function count(i, lessM, M), where i is the i-th bit being generated and lessM is a boolean which denotes whether the prefix of m before position i is less than the prefix of M before position i.

As noted earlier, we start generating the number from the most significant bit (the leftmost bit) to the least significant bit (the rightmost bit). Therefore, the base case is when i is -1 which implies we have successfully constructed a whole number m. For the base case we return 1 if the generated number m is less than M otherwise we return 0 (since we only want to count such m that is strictly less than M).

We can do Dynamic Programming by caching (memoizing) on the parameters i and lessM and the result. Here is a sample implementation in Python 3 (note that lru_cache provides the required memoization):

from functools import lru_cache

def getBit(num, i):
  return (num >> i) & 1  # Returns the i-th bit value of num.

@lru_cache(maxsize = None)
def count(i, lessM, M):
  if i == -1:  # The base case.
    return lessM  # only count if it is strictly less than M.

  maxM = lessM or getBit(M, i) == 1

  res = count(i - 1, maxM, M)  # Value 0 is always feasible. See (1) below.

  if maxM: # Value 1 is feasible if maxM is true. See (2) below.
    res += count(i - 1, lessM, M)  # See (3) below.

  return res

# Prints how many non-negative numbers that are less than 123456789
print(count(31, False, 123456789))

Notes:
(1): To compute the boolean value of lessM for the next bit of m in the recurrence, we look at the value of the current lessM. If the current lessM is already true, then lessM for the next bit in the recurrence will also be true. Another case when lessM for the next bit is true is when the i-th bit of M is equal to 1. Since we pick value 0 for the current (i-th) bit in m and it is less than the i-th bit of M (which is 1), it means that lessM is true for the next bit. maxM captures what we described just now, therefore the next value for lessM for the next bit in the recursion is set to maxM.
(2): Value 1 is feasible if lessM is true (which means we are free to use both values 0 and 1) or the i-th bit of M is 1 (which means we are still generating feasible partial number m that is less than or equal to M).
(3): The value for lessM in the next bit can only be true if lessM is previously true. If the current lessM is false, then we know that the i-th bit of M is 1. Since we picked value 1 for the current bit, the next value for lessM will not change (since 1 is not less than 1).

Now, with the above intuition for generating non-negative numbers that are less than M, we can generalize it to count all possible pairs (a,b) that are less than A and B respectively and where the bitwise ANDing of the pair (a,b) is less than K. We enumerate all possible values for current bit in a and b (i.e. the 4 possible values (0, 0), (0, 1), (1, 0), (1, 1)) and add new constraints to ensure that the bitwise ANDing of the pair (a,b) < K.

The code for the original problem is of a similar style as in the simpler problem. The code is presented below. The purpose of the variable lessA is equivalent to lessM, similar for lessB and lessK. We try to generate all feasible values for a and b and keep k in check (see the following notes).

@lru_cache(maxsize = None)
def countPairs(i, lessA, lessB, lessK, A, B, K):
  if i == -1:  # The base case.
    return lessA and lessB and lessK  # Count those that are strictly less.

  maxA = lessA or getBit(A, i) == 1
  maxB = lessB or getBit(B, i) == 1
  maxK = lessK or getBit(K, i) == 1

  # Use value 0 for a, b, and k which is always possible. See (1).
  count = countPairs(i - 1, maxA, maxB, maxK, A, B, K)

  if maxA:  # Use value 1 for a, and 0 for b and k. See (2).
    count += countPairs(i - 1, lessA, maxB, maxK, A, B, K)

  if maxB:  # Use value 1 for b, and 0 for a and k. See (3)
    count += countPairs(i - 1, maxA, lessB, maxK, A, B, K)

  if maxA and maxB and maxK:  # Use value 1 for a, b, and k. See (4)
    count += countPairs(i - 1, lessA, lessB, lessK, A, B, K)

  return count

Notes:
(1): If we choose 0 for a and 0 for b, the value for k should be 0 since 0 & 0 = 0
(2): If we choose 1 for a and 0 for b, the value for k should be 0 since 0 & 1 = 0
(3): If we choose 0 for a and 1 for b, the value for k should be 0 since 1 & 0 = 0
(4): If we choose 1 for a and 1 for b, the value for k should be 1 since 1 & 1 = 1

To avoid overflows, you should take care to use 64-bit integers. Also, this solution pattern is a standard way to solve these kinds of problems and can be generalized to any number system (and not just base 2 as was the case in our problem).

The complexity of this solution is based on the size of the DP table which here is 31 * 2 * 2 * 2.

Second approach

We can group the pairs (a, b) in S(A, B, K) based on whether a and b are odd or even, i.e. have the least significant bit set. Each such pair will be accounted for in one of the four sets below (written using set-builder notation), so summing up the sizes of the four sets will give us the value f(A, B, K).

1. {(a/2, b/2) | (a, b) ∈ S(A, B, K) && a even && b even}
   = S(ceil(A/2), ceil(B/2), ceil(K/2))
2. {(a/2, (b-1)/2) | (a, b) ∈ S(A, B, K) && a even && b odd}
   = S(ceil(A/2), floor(B/2), ceil(K/2))
3. {((a-1)/2, b/2) | (a, b) ∈ S(A, B, K) && a odd && b even}
   = S(floor(A/2), ceil(B/2), ceil(K/2))
4. {((a-1)/2, (b-1)/2) | (a, b) ∈ S(A, B, K) && a odd && b odd}
   = S(floor(A/2), floor(B/2), floor(K/2))

Note that in the 4 sets, the values for ‘k’ are forced. If ‘a’ or ‘b’ is even, ‘k’ will also be even while if both ‘a’ and ‘b’ are odd, then ‘k’ is also odd (because of the bitwise ANDing).

Let us provide more intuition on the 4 sets. We show it with an example where we list even numbers. If A is odd, e.g. 7 then the possible ‘a’ values that are even are 0, 2, 4, 6. If A is even, e.g. 8 then the possible ‘a’ values that are even are also 0, 2, 4, 6. The numbers in their binary representation are 000, 010, 100, 110. The 4 sets is akin to fixing (or eliminating) the least significant bit (i.e. by shifting right by 1, i.e. a>>1) which results in the set: 00,01,10,11 i.e. values 0, 1, 2, 3. The new value for A here is 4 (i.e. first integer greater than 0, 1, 2, 3). We generalize and say the following: If we are considering even values for ‘a’, then the new A is given by (A+1)>>1 (which is also ceil(A/2)). By going through a similar exercise for when ‘a’ is odd and A is odd or even (which we leave to the reader), we find the new A is given by A>>1 (which is also floor(A/2)).

The 4 sets give us a simple recursive procedure to compute f(A, B, K), as the sizes of the sets on the right hand side of the equations are simply calls to f. The appropriate base cases here are f(1, 1, K) = 1 and f(A, B, K) = 0 if any of A, B, K are equal to zero. To turn this recursive procedure into an efficient algorithm, we can memoize computed values. This means that after computing some f(A, B, K), we cache the result so future computations with the same values will take constant time.

Sample implementation in Python 3:

@lru_cache(maxsize = None)
def f(A, B, K):
    if A == 0 or B == 0 or K == 0:
        return 0
    if A == B == 1:
        return 1
    return f((A+1)>>1, (B+1)>>1, (K+1)>>1) + \
           f((A+1)>>1, B>>1, (K+1)>>1) + \
           f(A>>1, (B+1)>>1, (K+1)>>1) + \
           f(A>>1, B>>1, K>>1)

Complexity Analysis

It can be shown by induction that a recursive call f(A’, B’, K’) of recursive depth n has A’ equal to either floor(A / 2ⁿ) or 1+floor(A / 2ⁿ), and that B’ and K’ satisfy similar relations. From this, we can see that at a given recursive depth there are at most 8 different calls to f. Due to our chosen base cases, we can also see that the maximum recursion depth is O(log(max(A, B))). We conclude that the algorithm is O(log(max(A, B))).

We can model this problem as a graph problem where the cities are nodes in the graph and the bidirectional flight tickets between cities are the bidirectional edges connecting the nodes. Each node has a distinct zip code number. The given constraints on the tickets and how it should be used can be modelled as a modified depth-first-search-like traversal where: when we visit a node, we are not required to visit all of its neighbors but in the end all nodes must be visited. When a node is visited, its zip code is printed (i.e., pre-order traversal). When all nodes have been visited, the printed (concatenated) zip codes must form the smallest number possible.

Brute Force Solution:

The small input has at most 8 nodes. It is small enough that we can try all possible paths according to the rules (including all possible starting nodes), and pick the one with the smallest number (of concatenated zip codes). The brute force solution can have a time complexity of O(N! * N), where N! comes from having to potentially list all possible permutation of cities and for each permutation we can check its validity in O(N). As the large input can have up to 50 cities, this algorithm will be too slow. Therefore we propose an alternative solution to handle the large input.

Greedy Solution:

We can rank nodes based on its zip codes (i.e., the smallest node is the node with the smallest zip code). Since all of the zip codes are the same length, we can think of each zip code as a single digit number and to form the smallest concatenated digits we can just greedily concatenate the digits in increasing order. This means that the node with the smallest zip code should be the first node to be visited (i.e., the source node for the traversal). Thus, to minimize the final concatenated number, we should always visit the next smallest feasible node (we will discuss node feasibility later). Note that it is always possible to complete the traversal from the smallest node (or any node) since the input graph is connected.

Before we provide the pseudocode of the greedy algorithm, let’s define some variables. We provide examples that make use of these variables in subsequent paragraphs:

• DEAD: The set of nodes we’ve already visited and left (which we may never visit again).
• ACTIVE: The stack of nodes along our current path (originating from the source node).
• HEAD: The node at the top of the ACTIVE stack, which is the node we are currently on.

At each step, we may either:

• Visit some not-yet-visited neighbor of HEAD, which adds the newly visited node to the top of the ACTIVE stack and make it as the new HEAD. This action is analogous to flying to a new city for the first time. Note that when we visit a new city, we should concatenate its zip code to our final answer.
• Leave HEAD, which pops HEAD from the ACTIVE stack and moves it to the DEAD set. This action is analogous to taking the return flight from HEAD using the return ticket used to visit HEAD. Note that we do not concatenate the city’s zip code to the final answer when leaving the city.

With that, we are ready to present the pseudocode for our greedy algorithm:

  root = the node with smallest zip code
  DEAD = new Set()
  ACTIVE = new Stack()
  ACTIVE.push(root)
  answer = “”
  concatenate zipcode[root] to answer
  while ACTIVE is not empty:
    HEAD = ACTIVE.peek()
    next = next_smallest_feasible_node_to_visit()
    if next is EMPTY or no flight from HEAD to next:
      # leave the HEAD node
      insert HEAD to the DEAD set
      ACTIVE.pop()
    else:
      # visit the next node
      ACTIVE.push(next)
      concatenate zipcode[next] to answer
  print answer

Now, the hard part is: how do we compute the next_smallest_feasible_node_to_visit()? We first demonstrate it with an example.

Suppose we have a graph and we start traversing from the source node S (which has the smallest zip code). Suppose the next nodes with smallest zip codes are nodes A, B, C in that order and A is connected to S, B is connected to A, and C is connected to B. Then the greedy algorithm will go from S -> A -> B -> C. The figure below shows the current state of the traversal and the rest of the graph. Nodes S, A, B, C are in the ACTIVE stack where C is the HEAD:

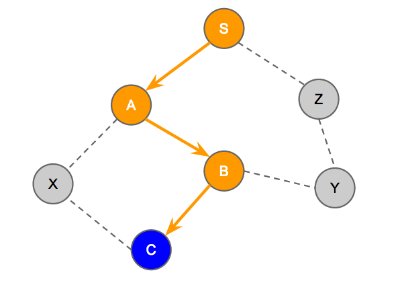
How do we pick the next smallest feasible node to visit from C? Could we arbitrarily pick a node that is connected to the ACTIVE stack then decide to visit that node next? Actually not. We investigate the following three scenarios to clarify why we cannot arbitrarily pick a node connected to the ACTIVE stack.

• Scenario 1: Z’s zip code is smaller than both X and Y
  In this case, we cannot visit Z as the next node since it requires us to travel back from C -> B -> A -> S, then visit Z. This will put nodes C, B, A in the DEAD set. This becomes a problem for node X since it has not yet been visited and now there is no way to reach node X from any ACTIVE nodes (note that as we cannot visit the DEAD nodes therefore the DEAD nodes A, B, C disconnect X from S, Z and Y). Thus, node Z is not feasible as the next node to be visited next (after C).
• Scenario 2: X’s zip code is smaller than Y’s, and Y’s is smaller than Z’s
  In this case, we can directly visit X from the currently active node C. Then, we can visit the next smallest node Y by traveling back from X -> C -> B -> Y. Finally, we visit the next smallest node Z directly from Y. After that, we can go back all the way to S via Z -> Y -> B -> A -> S to complete the traversal.
• Scenario 3: Y’s zip code is smaller than X’s, and X’s is smaller than Z’s
  In this case, we can visit the next smallest node Y by travelling back from C -> B -> Y while putting node C in the DEAD set. The next smallest node X can still be reached by traveling back from Y -> B -> A -> X and putting nodes B and Y in the DEAD set. Finally, the next smallest node Z can be visited by travelling back from X -> A -> S -> Z.

From the scenarios above, we know that Z is not feasible as the next node but both X and Y are feasible and we can visit the one with the smaller zip code first.

In general, we need to be able to figure out if a node is feasible as the next node. To do so, we can instead ask when is a node not feasible as the next node. It is not a feasible node if by visiting that node, some nodes that are not-yet-visited become unreachable from the nodes in the ACTIVE stack (i.e., they can never be visited later because they are disconnected from the ACTIVE set due to some nodes that will be placed in the DEAD set when taking the return flight as in Scenario 1). Observe that nodes that are still reachable from nodes in the ACTIVE stack can still be visited later.

To check whether the not-yet-visited nodes are still reachable from the ACTIVE nodes, we can do a connectivity check (via breadth-first-search or depth-first-search) from the source node to all the not-yet-visited nodes, avoiding the DEAD nodes. Note that since all ACTIVE nodes are all connected to the source node, doing the connectivity check from the source node is equivalent to doing the connectivity check from all ACTIVE nodes.

Now, we are ready to devise an iterative algorithm to find the feasible nodes and pick the smallest node. Referring to our example above, in this iterative algorithm we will generate X, Y and Z in that order. The algorithm will terminate when we reach Z (please refer to Scenario 1 for the reason). Note that when this algorithm returns, it should not alter the ACTIVE stack and the DEAD set. Therefore, when running this algorithm we can either make a local copy of the ACTIVE stack and the DEAD set, or restore the changes we made (if we run this algorithm in place). The iterative algorithm is as follows:

1. Check the neighbors of the current HEAD and record the next smallest node to visit.
2. Try to abandon the current HEAD node and take the return flight to the previous node in the ACTIVE stack. If it is not possible to abandon this HEAD (i.e., it makes some not-yet-visited nodes unreachable), then we stop and return the smallest node we recorded. Otherwise, we take the return ticket from HEAD (abandon the current HEAD) and keep on looping by going to step 1.

The following pseudocode shows one way to implement the above algorithm (with in place modification of the ACTIVE stack and DEAD set, and restoration of the changes before returning):

  def next_smallest_feasible_node_to_visit():
    temp = new Stack()
    best = EMPTY
    while ACTIVE is not empty:
      HEAD = ACTIVE.top()
      # Check the neighbors of HEAD and record the 
      # next smallest node as best.
      for each neighbor i of HEAD that is not-yet-visited:
        if best == EMPTY or zipcode[i] < zipcode[best]:
          best = i

      # Abandon HEAD and go back up in the ACTIVE stack.
      insert HEAD to the DEAD set
      temp.push(HEAD)
      ACTIVE.pop()

      if there exists a not-yet-visited node that \
        is not reachable from the source node:
        break

    # Restore the ACTIVE nodes and the DEAD set.
    while temp is not empty:
      HEAD = temp.top()
      remove HEAD from the DEAD set
      temp.pop()
      ACTIVE.push(HEAD)

    return best

How fast is this greedy algorithm? The greedy algorithm calls the search for the next smallest feasible node routine N times. Each search runs through all the nodes in the ACTIVE stack with at most O(N) nodes. For each node in the ACTIVE stack, we perform one connectivity check that takes O(N) time, and we loop through all of the node’s O(N) children. Therefore overall, it is O(N³), which fits easily into the time limits.