Google Code Jam Archive — Qualification Round 2014 problems

In the first arrangement, when the volunteer tells the magician the row that contains her card, the magician is able to see a set of four cards in that row. Similarly, in the second arrangement, the magician is able to see another set of four cards in the selected row.

Therefore, after hearing the two volunteer’s answers, the magician will have two sets of cards:
- the first set of four cards that lie in the selected row in the first arrangement, and
- the second set of four cards that lie in the selected row in the second arrangement.

To know which card the volunteer chose, the magician must be able to find exactly one card that is in both sets (i.e., the intersection size of the two sets must be equal to one). If there is more than one card that is in both sets (i.e., the intersection size is bigger than one), then it means the magician can not determine which card the volunteer chose since there are more than one possible card that could have been chosen by the volunteer (the magician did a bad job). If none of the card in the first set is in the second set (i.e., the intersection size is zero), then there is no card consistent with the volunteer's answers (the volunteer cheated).

The sample input covers all three possible cases:

In Case #1, the two sets are {5, 6, 7, 8} and {9, 10, 7, 12}. There is exactly one card (i.e., card 7) that is in both sets, and thus the volunteer chosen card must be 7.

In Case #2, the two sets are {5, 6, 7, 8} and {5, 6, 7, 8}. The card chosen by the volunteer can be any of {5, 6, 7, 8} because all of them contains in both sets. Bad magician!

Lastly, in Case #3, the two sets are {5, 6, 7, 8} and {9, 10, 11, 12}. None of the cards in the first set is in the second set. The volunteer must have cheated!

In this problem, we need to decide on the number of cookie farms to buy and also need to decide on when to buy the farms.

The strategy is perhaps surprisingly simple: first, collect enough cookies to buy a farm. Then figure out whether it's faster to buy one farm and then collect X cookies, or simply to collect X cookies now. If it's faster to collect X cookies now, you should do that. If it's faster to buy a farm first, buy that farm and then repeat this process (collect enough cookies to buy another farm...).

It's very easy to say that, but it's not as easy to prove it works. How many farms might you end up buying? If it's in the billions, your program might be too slow, and we never proved it wouldn't be. We also didn't prove that it's best to buy a farm right away as soon as you have enough cookies. The rest of this editorial will go into those questions in detail.

We build the intuition for the solution by using geometry. We represent the problem in the 2d plane. Let the x-axis represent time (in seconds) and the y-axis represent the number of cookies. Initially, we gain cookies at the rate of 2 cookies per second which is shown by line L₀ in Figure 1. Let’s say the target number of cookies (X) is 16. We can represent it with line y=16 (L_X). This means that if we do not buy any cookie farm then the time it takes to get 16 cookies is given by the intersection between L_X and L₀. See Figure 1.

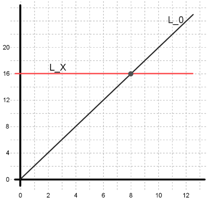
Figure 1

Now, let’s delve into what happens (geometrically speaking) when we buy a cookie farm. Let’s say the cost for buying a cookie farm (C) is 6, and the extra cookies per second (F) is 2. In Figure 2, we buy a farm as soon as we have 6 cookies. This means at time = 3, we go from having 6 cookies to 0 cookies (to pay for the cookie farm), and our cookies per second increases to 4. This information is represented by L₁ in Figure 2. Note that the dashed lines represent the drop of current cookies when we buy a cookie farm. Notice that L₀ and L₁ intersect at the 6 second mark (and correspondingly, X=12 cookies). It means that, if our target number of cookies X is anywhere between 0 and 12 then it is not advantageous to buy a cookie farm! Why? Let’s look at an example line L_Xa which is in that range. In Figure 2, we see that L₀ intersects L_Xa earlier (at 4 second mark) than L₁ intersects L_Xa (at 5 second mark). At X = 12 (represented by L_Xb), it does not matter if we buy a cookie farm or not. But if X is higher than 12, for example X = 16 (represented by L_X), we should buy a cookie farm since L₁ intersect L_X earlier (at 7 second mark) than L₀ (at 8 second mark). Jumping ahead briefly, we notice a similar behavior for the intersection between L₁, L₂ and L_X in Figure 4 (we'll describe how we compute L₂ in subsequent paragraphs). If we choose X = 18, it doesn't matter if we choose L₁ or L₂, but if X is below 18 then L₁ intersection is better than L₂ intersection, but if X is above 18 then L₂ intersection is better than L₁ intersection.

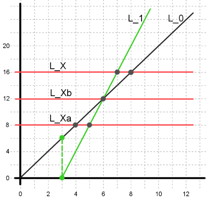
Figure 2

Now we discuss the strategy for how early we should buy a cookie farm i.e. should we buy a cookie farm as soon as we have C cookies, or should we wait a little longer before buying a cookie farm? We claim that we should buy a farm as soon as we have C cookies (and not wait any second longer).

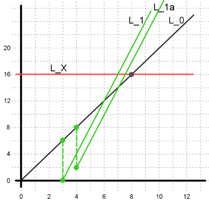
Figure 3

In Figure 3 as before, L₁ represents buying a cookie farm as soon as we have 6 cookies (at 3 second), while L₁a represents delaying buying a cookie farm by a second (at 4 second). Note that L₁ and L₁a are going to be parallel to each other (i.e. they have the same rate: 4 cookies for second) but L₁ is located to the left of L₁a. What does this mean? It means that the intersection between any line L_X and L₁ will always be at an earlier time than the intersection between L_X and L₁a. Therefore we should not wait to buy cookie farms any more than needed. This means that if buying a cookie farm contributes to your winning strategy, then we should buy a cookie farm as soon as possible, i.e. as soon as we have C cookies.

In Figure 4, we can observe that the earliest time to buy the first cookie farm is on the intersection of line L₀ with line L_C (y=C). Then, the earliest time to buy the second cookie farm is on the intersection of line L₁ with L_C.

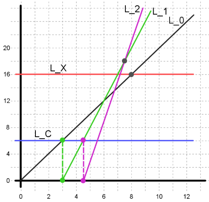
Figure 4

Now, we are ready to describe our solution strategy. We first determine the time t₀ it takes to get X cookies without buying a cookie farm (i.e. intersection between L₀ and L_X). Then we try to buy 1 cookie farm and figure out the time t₁ it takes to get X cookies (i.e. intersection between L₁ and L_X). Then compute t₂ for buying another cookie farm (i.e. intersection between L₂ and L_X), and so on. We stop when t_n+1 is greater than t_n (i.e. we do worse, in terms of time, by buying an additional cookie farm). For example, in Figure 4, we do worse with L₂ than with L₁ (intersections with L_X). We finally report t_n as our winning time.

A note on doing the actual line intersection computation follows. We want to compute the line intersections between lines L₀, L₁, L₂, etc and y = C or y = X. Let our current line be L_n starting at (S_n, 0) and have a slope of m (i.e. cookies per second after buying n cookie farms). Note that s₀ is 0, and m = 2 + n * F. Then the time required to get A cookies is given as: S_n + A / m.

Our solution strategy mentioned above iterates until a winning condition is achieved. But you might be wondering about total iterations needed before we are done. We want to point out that the number of iterations is bounded. In the solution strategy, we noted that the stopping condition for iteration is when we do worse (in terms of time) when buying an additional farm. Let’s formulate that as an equation. Let’s say our current iteration is i with line L_i with the next line being L_i+1. The intersection between line y = X and L_i is given as t_i = s_i + X / (2 + i * F), and similarly intersection between line y = X and L_i+1 is given as t_i+1 = s_i+1 + X / (2 + (i + 1) * F). We stop when t_i+1 > t_i. Note that s_i+1 - s_i = C / (2 + i * F). After going through some math, we get i > (X / C) - 1 - (2 / F), which is the iteration when t_i+1 becomes bigger than t_i. Therefore the iteration should terminate around X / C.

There are many ways to generate a valid mine configuration. In this analysis, we try to enumerate all possible cases and try to generate a valid configuration for each case (if exists). Later, after having some insight, we provide an easier to implement algorithm to generate a valid mine configuration (if exists).

Enumerating all possible cases

We start by checking the trivial cases:

• If there is only one empty cell, then we can just fill all cells with mines except the cell where you click.
• If R = 1 or C = 1, the mines can be placed from left to right or top to bottom respectively and click on the right-most or the bottom-most cell respectively.

If the board is not in the two trivial cases above, it means the board has at least 2 x 2 size. Then, we can manually check that:

• If the number of empty cells is 2 or 3, it is Impossible to have a valid configuration.
• If R = 2 or C = 2, valid configurations exists only if M is even. For example, if R = 2, C = 7 and M = 5, it is Impossible since M is odd. However, if M = 6, we can place the mines on the left part of the board and click on the bottom right, like this:

            ***....
            ***...c

If the board is not in any of the above case, it means the board is at least 3 x 3 size. In this case, we can always find a valid mine configuration if the number of empty cells is bigger than 9. Here is one way to do it:

• If the number of empty cells is equal or bigger than 3 * C, then the mines can be placed row by row starting from top to bottom. If the number of remaining mines can entirely fill the row or is less than C - 2 then place the mines from left to right in that row. Otherwise, the number of remaining mines is exactly C - 1, place the last mine in the next row. For example:

            ******        ******
            *****.        ****..
            ......   ->   *.....
            ......        ......
            .....c        .....c

• If the number of empty cells is less than 3 * C but at least 9, we first fill all rows with mines except the last 3 rows. For the last 3 rows, we fill the remaining mines column by column from the left most column. If the remaining mines on the last column is two, then last mine must be put in the next column. For example:

            ******        ******
            **....   ->   ***...
            **....        *.....
            *....c        *....c

Now, we are left with at most 9 empty cells which are located in the 3 x 3 square cells at the bottom right corner. In this case, we can check by hand that if the number of empty cells is 5 or 7, it is Impossible to have a valid mine configuration. Otherwise, we can hard-coded a valid configuration for each number of empty cell in that 3 x 3 square cells.

Sigh... that was a lot of cases to cover! How do we convince ourselves that when we code the solution, we do not miss any corner case?

Brute-force approach

For the small input, the board size is at most 5 x 5. We can check all (25 choose M) possible mine configurations and find one that is valid (i.e., clicking an empty cell in the configuration reveal all other empty cells). To check whether a mine configuration is valid, we can run a flood-fill algorithm (or a simple breath-first search) from the clicked empty cell and verify that all other empty cells are reachable (i.e., they are in one connected component). Note that we should also check all possible click positions. This brute-force approach is fast enough for the small input.

The brute-force approach can be used to check (for small values of R, C, M) whether there is a false-negative in our enumeration strategy above. A false-negative is found when there exist a valid mine configuration, but the enumeration strategy above yields Impossible. Once we are confident that our enumeration strategy does not produce any false-negative, we can use it to solve the large input.

An easier to implement approach

After playing around with several valid mine configurations using the enumeration strategy above, you may notice a pattern: in a valid mine configuration, the number of mines in a particular row is always equal or larger than the number of mines of the rows below it and all the mines are left-aligned in a row. With this insight, we can implement a simpler backtracking algorithm that places mines row by row from top to bottom with non-increasing number of mines as we proceed to fill in the next row and prune if the configuration for the current row is invalid (it can be checked by clicking at the bottom right cell). This backtracking with pruning can handle up to 50 x 50 sized board in reasonable time and is simpler to implement (i.e., no need to enumerate corner / tricky cases).

If the contest time were shorter, we may not have enough time to enumerate all possible cases. In this case, betting on the backtracking algorithm (or any other algorithm that is easier to implement) may be a good idea. Finding such algorithms is an art :).

Ken's best possible game of War

First, let's think about the best possible outcome for Ken in a game of War. Let's suppose the maximum number of points Ken can get is k; then after a little work convincing yourself, you should see that Ken can achieve that outcome if Ken's k heaviest blocks are played in decreasing order against Naomi's k lightest blocks, also in decreasing order.

That exact pairing likely won't happen, and without knowing Naomi's blocks' weights, Ken doesn't even know what the pairing would be; but Ken can follow a simple strategy to score k points anyway.

Ken's strategy

Ken's strategy is simple: when Naomi plays a block, Ken beats it with the lightest possible block if he can; and if he can't beat it, he plays his lightest block. It is clear that using such strategy will maximize Ken's winning potential for the following rounds because Ken not only wins one point for this round, but also preserves his heavier blocks for the following rounds.

The following block of text proves that this strategy will earn Ken the maximum possible number of points, k, no matter what Naomi does. If that's obvious to you, or you aren't into formal proofs, go ahead and skip it.

Proof

In this strategy, to win k points Ken wants to maintain an invariant: after Ken has scored i points, Ken's k-i heaviest blocks will still beat Naomi's k-i lightest blocks. When k-i is zero, Ken cannot win any more points because his heaviest block is lighter than any of Naomi's blocks. Therefore, if that invariant is maintained Ken must have k points when there are no more blocks left.

Proof of invariant:
Suppose Ken has i points. We'll refer to "pairs" of blocks later: Ken has k - i heaviest blocks remaining and his j-th heaviest remaining block is "paired" with Naomi's (k-i-j)-th lightest remaining block. There are three types of blocks Naomi might play:

1. If Naomi plays a block that's heavier than all of Ken's, it isn't from Naomi's lightest k-i blocks. Ken will play his lightest block which isn't from his heaviest k-i blocks, and the invariant is maintained.
2. If Naomi plays a block that's lighter than one of Ken's blocks but isn't from Naomi's lightest k-i blocks, Ken will either beat it with his heaviest block—in which case Naomi's lightest k-i-1 blocks will lose to Ken's heaviest remaining k-i-1 blocks, since nothing has changed about how the remaining blocks are paired—or Ken will beat it with something lighter, in which case his position is obviously no worse. Either way Ken has i+1 points and the invariant is maintained.
3. If Naomi plays a block from her lightest k-i blocks, Ken will either beat it with the block it's paired with, in which case Ken now has i+1 points and the remaining k-i-1 pairs are maintained; or Ken will beat it with something lighter, in which case Ken is clearly no worse off. Either way Ken has i+1 points and the invariant is maintained.

Naomi's best possible game of War

As we saw in the proof above, Ken can force his maximum possible number of points in War no matter what Naomi does. No wonder Naomi is tired of playing it!

Naomi's best possible game of Deceitful War

In Deceitful War, however, it turns out that the situation is exactly reversed: as we'll show in the following paragraphs. In War, Ken got the best possible pairings for himself but Naomi will get the best possible pairings for herself in Deceitful War.

Naomi's strategy for Deceitful War

There are several strategies for Naomi to play Deceitful War optimally. We present one here. Naomi's strategy for that is almost trivial. Assume k is the best possible score Naomi could achieve. Naomi can do score k points by pairing her k heaviest blocks with Ken's k lightest blocks.

Naomi will take her i-th heaviest block and tell Ken that it is heavier than all of Ken's blocks. Ken will believe her and play his lightest block, which is what Naomi wanted. Now Naomi simply has to repeat the process of playing her remaining heaviest blocks from lightest to heaviest and inciting Ken to play his lightest block from lightest to heaviest. After Naomi scores k points, her heaviest block will be lighter than any of Ken's available blocks. Now, since Naomi cannot lie anymore Naomi plays her remaining blocks without lying about their mass.

Conclusion

It's a particularly beautiful piece of symmetry that Ken can achieve his optimal pairing by being reactive, despite being honest and without information; and Naomi can reverse Ken's advantage by beating Ken's reactiveness with dishonesty and perfect information.