Google Code Jam Archive — World Finals 2013 problems
Overview
Ivan Miatselski (mystic) earns the 2013 Champion title.
The problem set for the 2013 finals was nearly impossible to solve in its entirety. This meant that the contestants had to be strategic in deciding which problems they were going to try their hand at if they wanted a chance to win the grand prize. The point values for the problems were 25, 29, 39, 43, 64, making problem E “Let Me Tell You a Story” by far the most important. Strangely enough, it was the high point value that perhaps was the reason problem E went unsolved: many contestants mentioned after the finals that they assumed it to be too difficult because of the high point value, explaining why they didn’t try too hard to crack it.
However, problem C “X Marks the Spot” suddenly took its place as the toughest problem that was still solved. Geometry problems are always hard no matter how easy they look, and only staniek (winner of Round 1C), managed to deal with all its tricks correctly in almost two hours: he spent one hour before trying to submit, submitted an incorrect solution for C-small, then found a bug (he was drawing the border directly through a gold mine) and fixed it in 30 more minutes, and then spent another 20 minutes before getting the large input done. That put him in the prime position to win the grand prize, and the spectators were waiting for him to solve the problems that proved to be quite tractable for other contestants and jump into the first place - but he lost his best shot at victory when the clock ran out on his attempt to solve D-large.
That left the prizes up for grabs for people who were solving problems A, B and D. The eventual top three all managed to solve those three problems completely, and also solve one or two other smalls. In third place was Russia’s winger: but spending almost an hour and a half on D made it difficult for him to challenge the first two contestants. In second place was Ukraine’s Vasyl, who was actually the first to get all of A, B and D solved. The winner was Belarus’s mystic, who overtook Vasyl in the last hour of the contest by solving E-small about 10 minutes earlier than his Ukrainian opponent, and then cementing his first place with C-small. Having placed second in 2011, mystic has finally made the final step - congratulations to him, and to all finalists!
Google Code Jam 2013 is over now, but Google Code Jam 2014 will be here before you know it. We’re looking forward to seeing you all again soon!
Cast
Problem A. Graduation Requirements Written by David Arthur, with Onufry Wojtaszczyk. Prepared by Onufry Wojtaszczyk.
Problem B. Drummer Written by Igor Naverniouk. Prepared by Jan Kuipers.
Problem C. X Marks the Spot Written by Onufry Wojtaszczyk, with Tomek Czajka. Prepared by John Dethridge and Tomek Czajka.
Problem D. Can't Stop Written by David Arthur and Bartholomew Furrow. Prepared by Tomek Kulczyński, with Bartholomew Furrow.
Problem E. Let Me Tell You a Story Written Igor Naverniouk, with Tiancheng Lou. Prepared by Tiancheng Lou.
Contest analysis presented by Topraj Gurung, Tsung-Hsien Lee, Denis Savenkov, Onufry Wojtaszczyk, Jonathan Paulson, Petr Mitrichev and Bartholomew Furrow.
Sample solutions, statement and input verification and other problem preparation by Karim Nosir, Jan Kuipers, Igor Naverniouk, Petr Mitrichev, John Dethridge, David Arthur, Onufry Wojtaszczyk, Bartholomew Furrow, Steve Thomas and Jonathan Wills.
A. Graduation Requirements
Problem
Before graduating from Awesome Programmer University, students traditionally perform certain "graduation requirements". One of these is driving around a traffic circle backwards. For most people, this is crazy enough, but as an extra challenge, you want to see if you can go backwards around the traffic circle multiple times without stopping.
The traffic circle consists of N intersections, spaced evenly around the circle. A car would normally enter the traffic circle at one intersection, and then every second, it will move to the next counter-clockwise intersection, until eventually it reaches its destination and leaves.
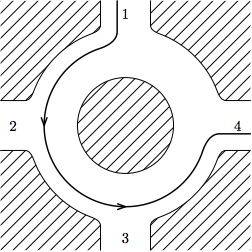
You have been watching cars enter and leave the traffic circle for X seconds. For each car, you record the time it enters the circle, as well as the intersections it enters and leaves at. All cars are moving counter-clockwise at the rate of 1 intersection per second. Each car you watched exited the circle before coming back to the intersection it entered at. There are multiple lanes on the traffic circle, so multiple cars can occupy the same position at the same time.
If you had planned it just right, how long could you have driven clockwise in the traffic circle during this time? You must enter the circle at some integer time >= 0, leave at time <= X, and once you leave, you are not allowed to come back. When in the traffic circle, you must travel clockwise at the rate of 1 intersection per second. You want to play it safe (well, as safe as driving backwards on a traffic circle can be), so you must never touch or pass by another car. In particular, you cannot leave the circle at an intersection at which another car is entering at the same moment, and you cannot enter the circle at an intersection at which another car is leaving at the same moment. You can choose when and where to enter and leave the circle.
Input
The first line of the input gives the number of test cases, T. T test cases follow. The first line of any test case describes the number C of cars you observed. The second line contains two integers, X and N — the time (in seconds) for which you observed the circle, and the number of intersections on the circle. Next C lines describe the cars you have seen. Each of those lines contains three integers si, ei and ti — the intersection at which the car entered the circle, the intersection on which it left and the time at which it entered. The intersections are numbered from 1 to N, counterclockwise (that is, the intersection number 2 is the next intersection counterclockwise from number 1).
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is the maximum number of seconds you can travel on the circle. Note that y can be zero both in the case where you cannot enter the circle at all and in the case when you can enter it, but can't travel even one intersection.
Remember that you are required to enter the circle at a time expressed as an integer number of seconds — you must enter at an integer time, and thus arrive at each intersection at an integer time.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 100
1 ≤ si, ei ≤ N
si ≠ ei
0 ≤ ti
Each observed car leaves the circle at time X or earlier.
Small dataset (Test set 1 - Visible)
3 ≤ N ≤ 10
1 ≤ X ≤ 10
0 ≤ C ≤ 10
Large dataset (Test set 2 - Hidden)
3 ≤ N ≤ 1010
1 ≤ X ≤ 1010
0 ≤ C ≤ 1000
Sample
5 1 3 4 1 4 0 6 3 5 5 2 0 5 1 2 1 3 0 1 2 2 2 3 0 3 4 0 3 2 3 1 3 0 2 1 0 3 2 0 0 6 4 1 2 3 1 3 0
Case #1: 1 Case #2: 2 Case #3: 0 Case #4: 6 Case #5: 0
In the first sample case, we have one car, going as in the picture in the statement. There are a number of ways allowing us to travel backwards for one second — for instance, we can enter at intersection 1 at time 1 (we can't enter at time zero, because the other car is there), and travel to intersection 4 (we can't go on to intersection 3, as we would pass the other car which will be going from 3 to 4). Another option is to enter at intersection 4 at time 0, and travel to intersection 3 (and then exit).
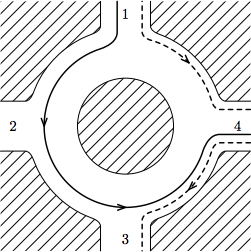
In the second sample case, we can travel for two seconds by entering at intersection 5 at time 1, and traveling backwards to intersection 3. In the third sample case, we can't even enter the circle - there are cars at all intersections at every full second. In the fourth case there are no cars, so we can just enter the circle at any point at time 0 and travel round and round till time 6. In the fifth case we can enter the circle, but since there are only three intersections, we will always collide with the other car if we try to move to the next one.
Note: Driving against the direction of the traffic on a traffic circle is typically not a wise thing to do and may cause harm to you or other people. Google (and Google Code Jam in particular) encourages you not to try this.
B. Drummer
Problem
The drummer has a very important role in any band -- keeping the rhythm. If the drummer's rhythm is uneven, it can ruin the entire performance.
You are the lead singer of a very popular rock band, and you have a bit of a problem. Your drummer has just quit the band to become a professional video gamer. You need to find a new drummer immediately. Fortunately, there is no shortage of candidates. Everyone wants a chance to join your band. Your task is to find the best drummer among the candidates, and you want the person who can keep the most consistent rhythm.
Your plan is as follows. You will ask each candidate to audition individually. During the audition, the candidate will play one drum by striking it with a drum stick several times. Ideally, the time difference between consecutive strikes should be exactly the same, producing a perfect rhythm. In a perfect rhythm, the drum strikes will have time stamps that follow an arithmetic progression like this:
In real life, of course, it is nearly impossible for a human to produce a perfect rhythm. Therefore, each candidate drummer will produce a rhythm that has an error E, such that each
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each one consists of two lines and represents the audition of one candidate. The first line contains a single integer -- N. The next line contains N integers separated by spaces -- the time stamps, in milliseconds, of the drum strikes played by the candidate. The time stamps are in increasing order.
Output
For each test case, output one line containing "Case #x: E", where x is the case number (starting from 1) and E is the smallest among all possible numbers that describe the error of the candidate's drum strike sequence.
Your answer will be considered correct if it is within an absolute or relative error of 10-6 of the correct answer. See the FAQ for an explanation of what that means, and what formats of floating-point numbers we accept.
Limits
Memory limit: 1GB.
1 ≤ T ≤ 100.
Small dataset (Test set 1 - Visible)
Time limit: 60 seconds.
2 ≤ N ≤ 10.
0 ≤ Ti ≤ 100.
Large dataset (Test set 2 - Hidden)
Time limit: 120 seconds.
For 90% of the test cases, 2 ≤ N ≤ 1000.
For all test cases, 2 ≤ N ≤ 50000.
0 ≤ Ti ≤ 106.
Sample
3 2 10 70 4 0 10 19 30 6 2 5 10 15 20 24
Case #1: 0 Case #2: 0.5 Case #3: 0.75
C. X Marks the Spot
Problem
Fair King Tyrone and his four sons conquered the nation of Carrania. His four sons immediately started to squabble about dividing the land between the four of them. The main point of contention was the gold mines of Carrania - each son wanted to have no fewer gold mines than any other.
Fair King Tyrone soon got tired of the squabbling, especially when he learned the number of mines is 4N, so dividing them should be easy. He gathered his sons, took a map, drew an X on it and declared each son would get one quarter of the nation, with borders defined by the X he drew.
Unfortunately, Fair King Tyrone is a bit shortsighted, and the map he drew on was not a map of Carrania. His first minister quickly hid the map, and now tries to draw an identical X on the map of Carrania so that each son gets the same number of gold mines. Unfortunately all sons saw King Tyrone draw the X, and know the borders should be two perpendicular straight lines - so the minister has to make them so.
Help him! Your task is to draw two perpendicular straight lines such that no gold mine lies on a border, and the borders divide the gold mines equally.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case begins with a number N, describing the number of gold mines each son should get. 4N lines follow, each containing two integers, being the coordinates xi, yi of one of the gold mines. No three gold mines are co-linear.
Output
For each test case, output one line containing "Case #x: xa ya xb yb", where x is the case number (starting from 1), (xa, ya) are the coordinates of the point where the two borders intersect, and (xb, yb) are the coordinates of some other point on the X.
All coordinates must be between -109 and 109, have at most 9 digits after the decimal point, and not use exponential notation. They must be exact: the resulting X will be drawn exactly at these coordinates. You should output IMPOSSIBLE instead if there is no good placement of borders.
Limits
Memory limit: 1GB.
1 ≤ T ≤ 20
-106 ≤ xi, yi ≤ 106
Small dataset (Test set 1 - Visible)
Time limit: 30 seconds.
1 ≤ N ≤ 10
Large dataset (Test set 2 - Hidden)
Time limit: 60 seconds.
1 ≤ N ≤ 2500
Sample
2 1 0 0 1 0 0 1 1 1 1 1 0 0 1 -1 0 0 -1
Case #1: 0.5 0.5 2 0.5 Case #2: 0 0 -3 -3
D. Can't Stop
Problem
This problem was inspired by a board game called Can't Stop, designed by Sid Sackson. This problem has a similar idea, but does not assume you have played Can't Stop.
You're playing a (very large) board game. In this game, you're given a sequence of N roll sets. Each roll set consists of D die rolls. Each die roll is an integer.
To win the game, you have to find the largest totally awesome interval of the sequence. An interval is any consecutive sequence of roll sets. An interval is called totally awesome if there exist k numbers such that every roll set in the interval contains at least one of those k numbers.
For example, suppose D=2 and k=3, and the roll sets are as follows:
Set 0: 10 20 Set 1: 50 60 Set 2: 70 30 Set 3: 40 40 Set 4: 30 30 Set 5: 20 40The interval from Set 0 to Set 2 is totally awesome because roll sets 0-2 all contain 10, 50 or 70. The interval from Set 1 to Set 5 is totally awesome because roll sets 1-5 all contain 50, 30 or 40. That interval contains 5 roll sets, and it is the largest totally awesome interval.
Your job is to output the indices of the first and last roll set in the longest totally awesome interval. If there are multiple totally awesome intervals of that length, output the indices for the one with the lowest first index. Note that the first roll set has index 0.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case starts with three space-separated integers: N, D and k, as described above. On the next line, there will be N*D integers. The first D integers will be the rolls from the first roll set; the second D integers will be the rolls from the second roll set; and so on.
Output
For each test case, output one line containing "Case #x: y z", where x is the case number (starting from 1), and y and z are the first and last indices of the longest totally awesome interval (with ties broken using the lowest index), as described above.
Limits
Memory limit: 1GB.
1 ≤ T ≤ 100.
1 ≤ D ≤ 4.
1 ≤ every die roll ≤ 105.
For 6 test cases, 1 ≤ N ≤ 105.
For all the other test cases, 1 ≤ N ≤ 103.
Small dataset (Test set 1 - Visible)
Time limit: 60 seconds.
k = 2.
Large dataset (Test set 2 - Hidden)
Time limit: 120 seconds.
2 ≤ k ≤ 3.
Sample
4 8 1 2 1 2 3 2 4 5 4 6 4 3 2 1 2 3 4 5 6 7 8 9 10 11 12 6 2 3 10 20 50 60 70 30 40 40 30 30 20 40 10 1 3 2 4 3 1 4 5 3 1 1 2
Case #1: 1 3 Case #2: 0 1 Case #3: 1 5 Case #4: 1 4
The board game Can't Stop was designed by Sid Sackson, and has been published by many publishers. Neither Mr. Sackson nor any of the publishers endorses, or has any involvement with, Google Code Jam.
E. Let Me Tell You a Story
Problem
The story goes...
A long, long time ago, King Tyrone the Fair had 4 ministers. The first minister (the king's top adviser) was paid 7 gold pieces per week. The second minister was paid 4 gold pieces per week. The third and fourth ministers were each paid 6 gold pieces per week. Unfortunately, Tyrone accidentally forgot the Ministerial Compensation List in the photo copier one day, and the List ended up on the front page of the Kingdom Times newspaper. At this point, the second minister requested to speak to the king, upset that his own salary was lower than that of the lower ranked third minister.
His Fairness King Tyrone saw no other solution than to fire the third minister. After all, lowering the third minister's salary, raising the salary of the second minister, or changing job titles were all unfair solutions to the problem, in the king's opinion. And who are we to question King Tyrone? Of course, firing the third minister did not solve the problem. The second minister continued to complain because his salary was still lower than that of the fourth minister. So King Tyrone fired the fourth minister as well. At this point, neither of the two remaining ministers complained, and everyone lived happily ever after.
...wait a minute. I messed that up. I'm sorry. My memory is not what it used to be. One moment please... Right. King Tyrone the Fair. Four ministers. Paid 7, 4, 6, and 6 respectively. Ah, yes. The ending went like this...
When the second minister complained of unfairness, King Tyrone fired the first minister. Some might say this was a bit harsh, as the first minister wasn't involved in any way, but we shouldn't question King Tyrone. Obviously, the second minister still complained, so King Tyrone simply fired him. Of the remaining two ministers, each one was being paid at least as much as any minister below him, so none of them complained. And everyone lived happily ever after.
Much better... I think. Maybe? Now I'm not sure anymore. I know for certain that there were N ministers, and I clearly remember their salaries. I also know that every time a minister's salary was lower than the salary of a minister below him, somebody would complain, and some minister got fired; but that it could have been any minister, regardless of whether that minister had anything at all to do with the problem. Ministers continued to be fired until no one complained because all of the salaries were non-increasing. At that point, the firings stopped. But I do not remember in which order the ministers got fired.
Can you help me fix my story? Or at least please tell me how many different stories I could have told. Two stories are different if the sequences of fired ministers in them are not the same.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each one consists of two lines. The first line will contain an integer N, and the second line will contain N space-separated integers denoting the ministers' salaries, in order from the first minister to the N'th minister.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is the number of stories I could tell you, modulo 10007.
Limits
Memory limit: 1GB.
Each salary will be positive and at most 10000.
Small dataset (Test set 1 - Visible)
Time limit: 60 seconds.
1 ≤ T ≤ 100.
1 ≤ N ≤ 100.
Large dataset (Test set 2 - Hidden)
Time limit: 120 seconds.
1 ≤ T ≤ 20.
For 80% of test cases, 1 ≤ N ≤ 2000.
For all test cases, 1 ≤ N ≤ 8000.
Sample
3 4 7 4 6 6 8 90 80 70 60 50 50 40 30 2 7 8
Case #1: 14 Case #2: 1 Case #3: 2
Analysis — A. Graduation Requirements
In this problem we are interested in finding the maximum time we can drive against the direction in a traffic circle. For small test cases, the size of the input is small enough to try all possible intersections, time to start, and check the length to drive without touching any other car.
For large test cases, the above approach is not good enough due to the extremely large N and X (up to 1010). Therefore in order to solve the large test cases, we transform the problem into the 2-dimensional plane with intersection and time as axes. Then, each car can be represented as line segments; your car will be represented as a line segment orthogonal to other line segments formed by other cars. Figure 1 shows the second sample test case. Lined segments corresponding to different cars are denoted with different colors while the black dotted segment corresponds to your car. Note that as the intersections are in a traffic circle, we show it by repeating intersection 5 and 1 on the two ends in Figure 1.
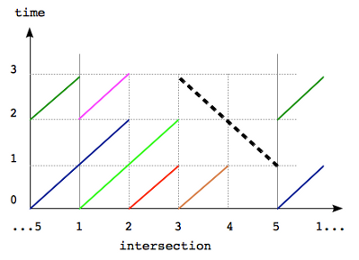
Figure 1
So the problem can be reformulated as follows: given a set of line segments, find the maximum possible length of a perpendicular segment which does not touch any other segment. Note that if two segments have a point in common the corresponding cars touch each other.
To solve the large test case one needs to notice that a line segment of maximum possible length can be chosen so that it goes near one of the endpoints of another segment. By “near” we mean distance = 1 in one of the axes. Indeed, if we have a segment of maximum possible length, that does not go near one of the endpoints, we can always move it so that it does, see Figure 2 for an example.
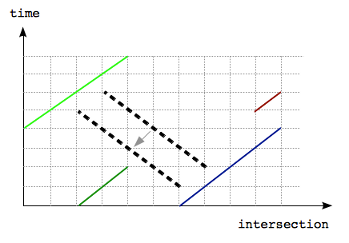
Figure 2
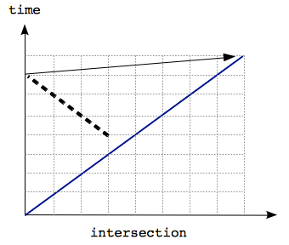
Figure 3
The statement is also true in examples such as in Figure 3 because intersections are arranged in a circular manner and the solution segment is near the top right endpoint which is shown with an arrow.
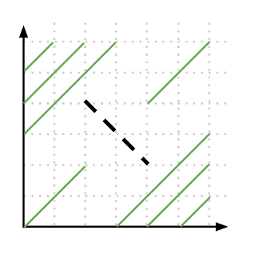
Figure 4
Thus we note that changes in the length of segments happen near these endpoints. Therefore to solve the problem we need to go over all endpoints of car segments and consider its neighbourhood (-1 and +1 in both of the axes). Note that we also need to consider segments that go through endpoints +/-(1,1), an example is shown in Figure 4. Then we can compute all segments that pass through these near points and pick the longest segment as the answer.
For each such candidate point, we need to check how far up and down a segment that go through the candidate point can reach without touching other segments. This can be done simply by going over all car segments and checking if and where our candidate segment intersect them. The complexity of this algorithm is O(C2), which is enough to solve the large case.
Analysis — B. Drummer
This problem can be viewed as a modified version of finding the minimum width of a convex hull [1] which can be solved using a modified version of the rotating calipers technique [2,3]. We present below the intuition on why the problem is similar to finding the modified minimum width of the convex hull.
First off, we can plot the sequence of drum strikes as (i, Ti )on the 2-dimensional plane. If the drummer performs perfectly, then let's call the sequence Pi and (i, Pi) falls on the same line L (see Figure 1 and Figure 2).
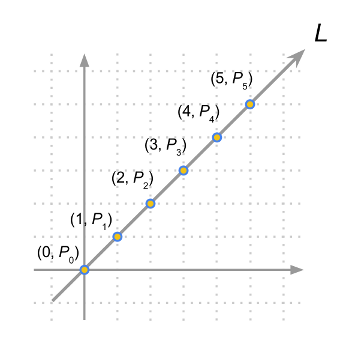
Figure 1
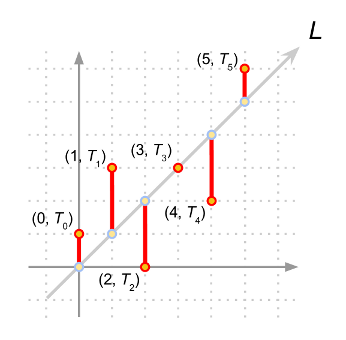
Figure 2
Unfortunately the drummer does not perform perfectly and has error Ei (which is |Ti - Pi|) (see Figure 3).
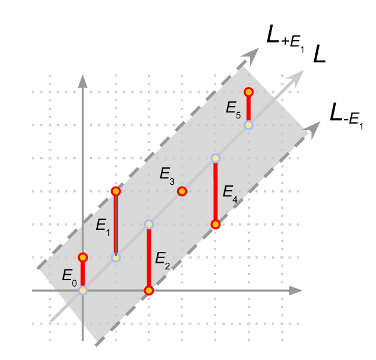
Figure 3
So in the example in Figure 3, we have our line L, and it is clear that our answer is the maximum among all Ei, which in this case is E1 (or E2 or E4). If we draw two lines parallel to L shifted in the y-axis by +E1 and -E1, denoted as L+E1 and L-E1 (see Figure 3), you will notice that the region between the two lines contains all the points (i, Ti); this example fits the definition of the problem which is a drum rhythm where each strike differs by at most E from some perfect rhythm. On the other hand, if we choose E5 as the error candidate, the region between the two lines L+E5 and L-E5 will not contain all the points (i, Ti) (see Figure 4).
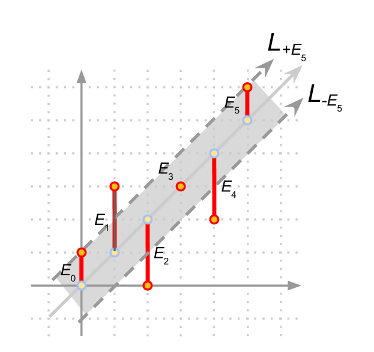
Figure 4
In essence, we want to find a line denoting the perfect rhythm and two parallel lines that are shifted in the y-axis by +E and -E such that the two parallel lines contain all the points (i, Ti) and also that E is the minimum possible value. We would like to point out that instead of trying to find the line with the perfect rhythm which can be a hard problem due to the error associated with each (i, Ti), we can instead focus on the equivalent problem of finding the two parallel lines. Note that each of these two lines must touch at least one point otherwise we can always reduce the distance between these two lines, and further reduce the distance on y-axis to get a smaller error E.
In fact, all candidate parallel lines touch (without intersecting) the convex hull of the points (i, Ti). Therefore we transform the problem to finding the minimum distance between two parallel lines in y-axis touching (without intersecting) the convex hull. For example, the convex hull of the points in Figure 2 are shown in Figure 5.
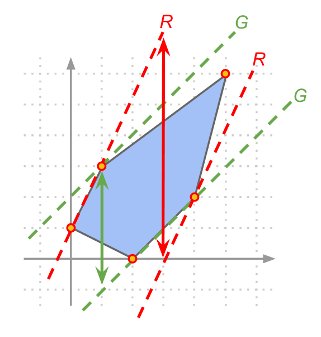
Figure 5
Therefore to solve this problem, we first compute the convex hull of the points (i, Ti). Then we go through all the line segments on the boundary of the convex hull and find the corresponding parallel line on the opposite side of the convex hull (see Figure 5 for some examples), then get the y-distance between these two parallel lines, and report the minimum among all such y-distances.
Analysis — C. X Marks the Spot
Median choice
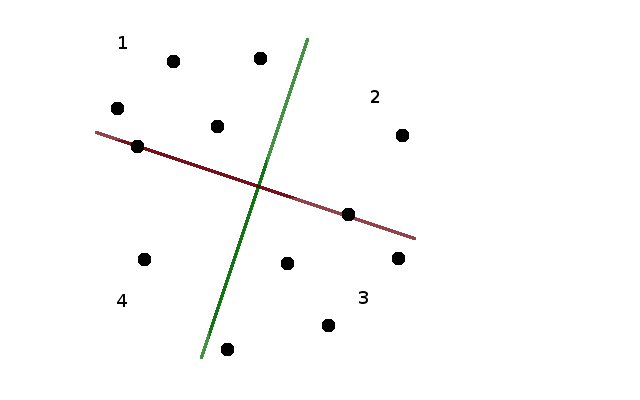
Since the four quarters formed by the two lines have to contain the same number of mines, each of the two lines has to split the set in half. Thus, if we know the inclination of the two lines (given as, e.g., the directed angle the first line forms with the horizontal axis), we can position the each line in any place such that it splits the points in half (by, for instance, sorting the points by the value of the cross-product with the direction of the line). Let's begin by choosing any angle alpha as our initial angle, and draw the two lines according to the procedure above.
Suppose that the first quarter contains X points. The second quarter contains 2N - X, since there have to be 2N points above the red line. The third quarter will again contain X points (because there are 2N points to the right of the green line), and the fourth will contain 2N - X. So if X = N, our two lines are a correct solution. This doesn't need to be the case, though, as we can see on the figure above.
Rotating the lines
If the angle alpha we chose happens not to be a correct solution to the problem, we will try rotating the lines (by increasing alpha) until it becomes valid.
Let's consider what happens when we rotate the lines. At some moment, one or both of the lines will rotate to a point where instead of splitting the set neatly in half, the "splitting line" passes through two mines, with 2N-1 mines on either side (note that we are taking advantage of the fact that no three points are collinear, so we know the line passes through exactly two points, and not, say, four). We will call the moment at which there are two points on at least one of the splitting lines a "discontinuity". After we rotate a tiny bit more, the lines split the set neatly again.
We will prove in a moment that at any discontinuity, X changes at most by one (it can also happen to stay the same). Notice, however, that when we increase alpha by 90 degrees, the red and green lines will exchange places, which means that the first quarter (which also rotated by 90 degrees) now contains 2N-X points. Thus, somewhere in between X had to be exactly equal to N!
Discontinuity
Let's analyze what happened after the discontinuity. Obviously, only the points that were on the dividing lines could have changed quarters at the discontinuity. One of the points that were on the red line crosses from one of quarters (1, 2) to one of quarters (4, 3), and the other point crosses in the other direction. Thus, if the discontinuity had points on one line only, X changes by at most one.
We will see that even if there were points on both lines at the discontinuity, X will still change only by one. The points on the red line go from quarters (1, 4) to quarters (2, 3). So, for X to, say, grow by two, we would have to have a point from 2 go to 3 and point from 4 go to 1 on the red line, while a point from 4 went to 3 and a point from 2 went to 1 on the green line. However, the red line (and the green line as well, but for now it's the red line that matters) is rotating clockwise - thus, it's the more leftward point that will go down, and the more rightward point that will go up — so the situation described above is impossible.
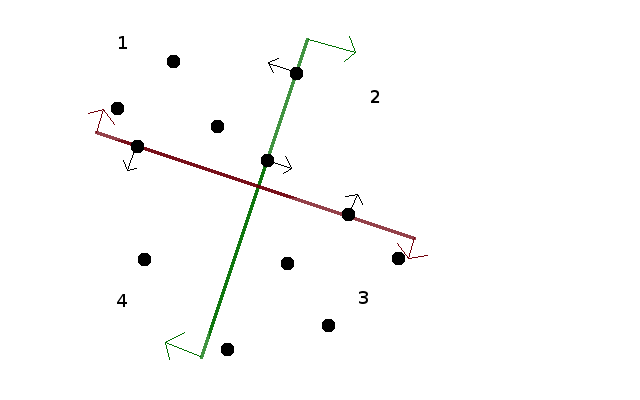
Finding the solution
We can now use binary search to find a solution to the problem. Begin with an arbitrary angle alpha as the left bound, and alpha + 90 degrees as the right bound, assume that for the left bound X is smaller than N (if it's equal, we're done, and if it's larger, take alpha + 90 as left and alpha + 180 as right). We know somewhere between the two there is a point in which X = N. So we pick an angle midway between left and right, and check how big is X for this median angle. If it's equal to N, we are done. If it's smaller, the median angle is our new left, if it's larger, it's the new right. Proceed until success.
A single iteration, with the standard implementation, takes O(N logN) time - sort the points twice, assign each to the appropriate quarter, find X. If somebody cared enough (one doesn't need to in this problem) it can be done in O(N) time, using a faster algorithm to find the median values (either a randomized one, like quicksort, but recursing only into the bigger of two halves, or even deterministically with the median of medians algorithm.
The key question is "how many iterations of the binary search algorithm will we need to find the angle we are looking for?". This depends on the size of the interval of angles that we will try to hit. This interval will occupy the space between some two discontinuities, and each discontinuity is defined by a line connecting two of the input points - thus, the size of the interval can be expressed as an angle between two lines, each crossing two points with integral coordinates no larger than 10-6. Such an angle can be on the order of 10-12, which means we will need roughly 40 steps of the binary search. Thus, our algorithm will easily run in time.
Precision issues
There are three types of precision issues that can hit one on the solving of this problem.
First, it can happen that one of the lines we choose happens to be a discontinuity. This can be either worked around (by choosing a median angle a bit to the left or right - there are only finitely many discontinuities, after all), or avoided by choosing a random angle to begin with - since there are finitely many discontinuities, it's very unlikely to hit one. It's also possible to choose a deterministic angles to avoid discontinuities.
Second, the interval of angles that we are trying to find can happen to be rather small, and so we will need many iterations of the binary search. This means that we need to use relatively high precision numbers to deal with the quantities involved. It's a pretty standard issue in geometry problems, though, and shouldn't surprise anyone.
Third, there are limits on the precision with which we can output the result, and the checker for the problem will check whether the output values are correct. Since there is a finite precision of the output, there will be some rounding happening. This means that if we were unlucky, and our chosen angle happened to be quite close to the boundary of the "good" interval, the rounding can push it out of the interval. There are two things we can do to mitigate this. First, we can add a few more steps of the binary search to find a few more points within the good interval, and then choose for our answer a point that we know is relatively far from the edge. Second, we should use all the precision that we are allowed in the input. In particular, when we know the line we want to draw, we should choose the second point we output (the one other than the crossing) to be as far away from the crossing as the limits on the output allow us, to minimize the error in the angle of the line resulting from rounding.
Analysis — D. Can't Stop
There is a nice divide-and-conquer solution. Split the input down the middle; the best interval is either entirely in the left half, entirely in the right half, or crosses the middle. We handle the right and left cases recursively; if we can handle the "crosses" case in linear time, we will have an O(N lg N) algorithm, which is good enough.
If the best interval crosses the middle, we know it must use the middle element, so we must pick one of the D numbers in that roll to use. Now go out as far as we can to the left and right with that number. Once we stop, we can extend either to the left or the right, so there are 2D different numbers to try. Expand again, and get 2D more numbers to try for a final expansion. In total, we only tried D*2D*2D different choices, so the whole thing runs in 256N time, and we get our O(N lg N) time algorithm.
Note: surprisingly for a divide and conquer algorithm, we don't use any information from the left and right halves to solve the middle case; the fact that it crosses is enough.
Slow and Simple
There's another set of approaches to this problem. Try every starting position, expanding out to the right and only making choices when necessary (just as in the divide-and-conquer). This is O(DK * N) for each starting position, or O(DK * N2) overall, which is too slow. However, there are several different improvements (some small, some large) one could make in order to make this linear in N.
Linear Time
One improvement works in this way: Every time you pick a number, check if the roll before your starting position contains that number. If so, we can safely ignore that choice (because we would have done better starting one roll earlier and choosing the same set of numbers).
It turns out that this runs in linear time, but the reason why isn't obvious. We want to prove that a particular index i is only visited from O(1) starting positions. Imagine we have reached i from start. Now imagine starting at i and going leftward (as usual, we expand left as far as possible before picking each new number). If we only choose numbers from the set that got us from start to i, we must get back to start (and no further, since the optimization above guaranteed that start - 1 doesn't contain any of our numbers). But there are only 1 + D + D2 + D3 different choices of numbers starting from i, so there are only that many possible positions for start, so i will only be visited O(D3) times.
Analysis — E. Let Me Tell You a Story
Dissecting the problem
The problem statement asks for the number of ways to remove elements from a sequence until we obtain a non-increasing sequence. Looking at the problem from the end, suppose we know the final non-increasing sequence, and it's of length K. Certain elements have been eliminated, and we removed N-K elements in total. There are (N-K)! (factorial of N-K) ways to remove those elements. So the first approximation seems to be to sum those factorials over all non-increasing subsequences of the the original sequence.
However, this is not entirely correct. Some non-increasing subsequences are not even reachable since we stop as soon as our sequence becomes non-increasing. For example, in the second example from the problem statement the sequence is non-increasing from the start, so no proper subsequence is reachable at all. For subsequences that are reachable, not every way of reaching them might be possible. For example, in the first example from the problem statement we can reach the '7 <first 6>' subsequence (note, it should be considered different from '7 <second 6>' subsequence) by eliminating the second 6, and then 4. However, it can't be reached by doing those operations in reverse order, since we'd stop right after eliminating 4.
Now instead of all (N-K)! ways to reach a certain subsequence, we need to count just the possible ways. The main trick in solving this problem is: let's count the impossible ways instead, and then subtract. The impossible ways are simply those when before the last removal, the subsequence was already a non-increasing sequence of length K+1. And for each such subsequence there are exactly K+1 ways to make an impossible removal and arrive at a subsequence of length K. That means the sum of numbers of impossible ways to reach all non-increasing subsequences of length K is equal to the total number of non-increasing subsequences of length K+1 times (N-K-1)! (the number of ways to reach the longer subsequence) times K+1.
To summarize, suppose AK is the number of non-increasing subsequences of length K. Then the answer to this problem is sum over K of AK*(N-K)!-AK+1*(N-K-1)!*(K+1).
Solving the sub-problem
We've now reduced our problem to a much simpler one: find AK. This problem can be solved used a somewhat standard dynamic programming approach, with a twist to make it run faster.
First, let's assume that all input numbers are different, and between 0 and N-1. It's not hard to transform them in this way without changing the answer. If there are equal numbers, we'll slightly reduce the number to the right, so that non-increasingness of all subsequences is preserved.
Our dynamic programming problem will now be: what is the number of non-increasing subsequences of length P that end with number Q? Let's call that number BP,Q. We will find them in the order Qs appear in the sequence.
It's not hard to see that BP,Q is just the sum of BP-1,Q' for all numbers Q' that are greater than Q and appear before Q in the sequence. Since we process the states in the order Qs appear in the sequence, we just need to take the sum over all Q' that are greater than Q.
This is already a working solution for our problem, but it is a bit too slow: it runs in O(N3) which is a bit too much for N=8000. We have O(N2) states in our dynamic programming, and we need to find a sum of O(N) numbers to process each state. However, we can compute such sum faster! We just need an array-like data structure that supports changing elements and finding the sum of its suffix (over all Q' that are greater than Q), and the Fenwick tree is a data structure that does exactly that, performing each operation in O(logN) time, for a total running time of O(N2*logN).