Google Code Jam Archive — Round 1B 2013 problems
Overview
Round 1B attracted nearly 5000 participants fighting for the 1000 spots that gave qualification to Round 2. The first problem our contestants faced was game-based Osmos with a greedy solution; over 3500 contestants managed to figure it out. This was followed by Falling Diamonds, where you had to calculate the probability of getting a diamond; a significant number of contestants had a hard time with getting the small input right. See the analysis of the problem for our ideas on how to solve it!
The final problem of this round was Garbled Email, which was much more accessible than Round 1A's Good Luck, with over 200 successful submissions for the large. This required some insightful string manipulation to handle a huge dictionary we provided.
119 contestants managed to get a full score from this round, led by Indonesia's dolphinigle, who finished all the problems in a bit over an hour. To advance to Round 2 you needed either the large of one of the two more difficult problems, large of Osmos and the small of Falling Diamonds, or large of Osmos, small of Garbled Email, and a really impressive speed!
Congratulations to the top 1000, and we hope you enjoyed the problems in this round!
Cast
Problem A. Osmos written by Bartholomew Furrow. Prepared by Zhen Wang and Bartholomew Furrow.
Problem B. Falling Diamonds written by Onufry Wojtaszczyk. Prepared by Alex Fetisov and Tomek Czajka.
Problem C. Garbled Email written by Bartholomew Furrow. Prepared by Jonathan Wills and Bartholomew Furrow.
Contest analysis presented by Onufry Wojtaszczyk and Bartholomew Furrow. Solutions and other problem preparation by Igor Naverniouk, Ahmed Aly, Tomek Kulczynski, Hackson Leung, Karim Nosseir, Hao Pan, Md. Arifuzzaman Arif, Sean Henderson and John Dethridge.
A. Osmos
Problem
Armin is playing Osmos, a physics-based puzzle game developed by Hemisphere Games. In this game, he plays a "mote", moving around and absorbing smaller motes.
A "mote" in English is a small particle. In this game, it's a thing that absorbs (or is absorbed by) other things! The game in this problem has a similar idea to Osmos, but does not assume you have played the game.
When Armin's mote absorbs a smaller mote, his mote becomes bigger by the smaller mote's size. Now that it's bigger, it might be able to absorb even more motes. For example: suppose Armin's mote has size 10, and there are other motes of sizes 9, 13 and 19. At the start, Armin's mote can only absorb the mote of size 9. When it absorbs that, it will have size 19. Then it can only absorb the mote of size 13. When it absorbs that, it'll have size 32. Now Armin's mote can absorb the last mote.
Note that Armin's mote can absorb another mote if and only if the other mote is smaller. If the other mote is the same size as his, his mote can't absorb it.
You are responsible for the program that creates motes for Armin to absorb. The program has already created some motes, of various sizes, and has created Armin's mote. Unfortunately, given his mote's size and the list of other motes, it's possible that there's no way for Armin's mote to absorb them all.
You want to fix that. There are two kinds of operations you can perform, in any order, any number of times: you can add a mote of any positive integer size to the game, or you can remove any one of the existing motes. What is the minimum number of times you can perform those operations in order to make it possible for Armin's mote to absorb every other mote?
For example, suppose Armin's mote is of size 10 and the other motes are of sizes [9, 20, 25, 100]. This game isn't currently solvable, but by adding a mote of size 3 and removing the mote of size 100, you can make it solvable in only 2 operations. The answer here is 2.
Input
The first line of the input gives the number of test cases, T. T test cases follow. The first line of each test case gives the size of Armin's mote, A, and the number of other motes, N. The second line contains the N sizes of the other motes. All the mote sizes given will be integers.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is the minimum number of operations needed to make the game solvable.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 100.
Small dataset (Test set 1 - Visible)
1 ≤ A ≤ 100.
1 ≤ all mote sizes ≤ 100.
1 ≤ N ≤ 10.
Large dataset (Test set 2 - Hidden)
1 ≤ A ≤ 106.
1 ≤ all mote sizes ≤ 106.
1 ≤ N ≤ 100.
Sample
4 2 2 2 1 2 4 2 1 1 6 10 4 25 20 9 100 1 4 1 1 1 1
Case #1: 0 Case #2: 1 Case #3: 2 Case #4: 4
Notes
Although the size of motes is limited in the input files, Armin's mote may grow larger than the provided limits by absorbing other motes.
Osmos was created by Hemisphere Games. Hemisphere Games does not endorse and has no involvement with Google Code Jam.
B. Falling Diamonds
Problem
Diamonds are falling from the sky. People are now buying up locations where the diamonds can land, just to own a diamond if one does land there. You have been offered one such place, and want to know whether it is a good deal.
Diamonds are shaped like, you guessed it, diamonds: they are squares with vertices (X-1, Y), (X, Y+1), (X+1, Y) and (X, Y-1) for some X, Y which we call the center of the diamond. All the diamonds are always in the X-Y plane. X is the horizontal direction, Y is the vertical direction. The ground is at Y=0, and positive Y coordinates are above the ground.
The diamonds fall one at a time along the Y axis. This means that they start at (0, Y) with Y very large, and fall vertically down, until they hit either the ground or another diamond.
When a diamond hits the ground, it falls until it is buried into the ground up to its center, and then stops moving. This effectively means that all diamonds stop falling or sliding if their center reaches Y=0.
When a diamond hits another diamond, vertex to vertex, it can start sliding down, without turning, in one of the two possible directions: down and left, or down and right. If there is no diamond immediately blocking either of the sides, it slides left or right with equal probability. If there is a diamond blocking one of the sides, the falling diamond will slide to the other side until it is blocked by another diamond, or becomes buried in the ground. If there are diamonds blocking the paths to the left and to the right, the diamond just stops.
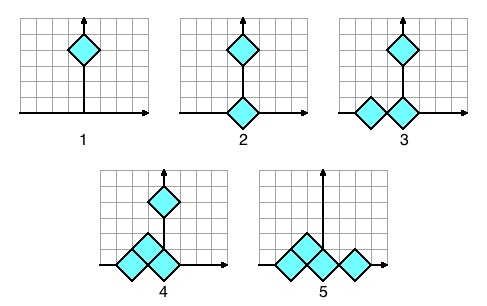
Consider the example in the picture. The first diamond hits the ground and stops when halfway buried, with its center at (0, 0). The second diamond may slide either to the left or to the right with equal probability. Here, it happened to go left. It stops buried in the ground next to the first diamond, at (-2, 0). The third diamond will also hit the first one. Then it will either randomly slide to the right and stop in the ground, or slide to the left, and stop between and above the two already-placed diamonds. It again happened to go left, so it stopped at (-1, 1). The fourth diamond has no choice: it will slide right, and stop in the ground at (2, 0).
Input
The first line of the input gives the number of test cases, T. T lines follow. Each line contains three integers: the number of falling diamonds N, and the position X, Y of the place you are interested in. Note the place that you are interested in buying does not have to be at or near the ground.
Output
For each test case output one line containing "Case #x: p", where x is the case number (starting from 1) and p is the probability that one of the N diamonds will fall so that its center ends up exactly at (X, Y). The answer will be considered correct if it is within an absolute error of 10-6 away from the correct answer. See the FAQ for an explanation of what that means, and what formats of floating-point numbers we accept.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 100.
-10,000 ≤ X ≤ 10,000.
0 ≤ Y ≤ 10,000.
X + Y is even.
Small dataset (Test set 1 - Visible)
1 ≤ N ≤ 20.
Large dataset (Test set 2 - Hidden)
1 ≤ N ≤ 106.
Sample
7 1 0 0 1 0 2 3 0 0 3 2 0 3 1 1 4 1 1 4 0 2
Case #1: 1.0 Case #2: 0.0 Case #3: 1.0 Case #4: 0.75 Case #5: 0.25 Case #6: 0.5 Case #7: 0.0
C. Garbled Email
Problem
Gagan just got an email from her friend Jorge. The email contains important information, but unfortunately it was corrupted when it was sent: all of the spaces are missing, and after the removal of the spaces, some of the letters have been changed to other letters! All Gagan has now is a string S of lower-case characters.
You know that the email was originally made out of words from the dictionary described below. You also know the letters were changed after the spaces were removed, and that the difference between the indices of any two letter changes is not less than 5. So for example, the string "code jam" could have become "codejam", "dodejbm", "zodejan" or "cidejab", but not "kodezam" (because the distance between the indices of the "k" change and the "z" change is only 4).
What is the minimum number of letters that could have been changed?
Dictionary
The dictionary contains W words of at least 1 and at most 10 lower-case characters and is given at the start of the input file. It is not a dictionary from any natural language, though it does contain some English words. The dictionary is the same for all test cases in a single input file. The dictionary is given in lexicographically increasing order and does not contain duplicate words.
Input
The first line of the input gives the number of words in the dictionary, W. Each of the next W lines contains a string of lower-case characters a-z representing a word in the dictionary. The next line of the input gives the number of test cases, T. T test cases follow. Each test case consists of a single line containing a string S, consisting of lower-case characters a-z.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is the minimum number of letters that could have been changed in order to make S.
Limits
Memory limit: 1GB.
W = 521196.
Each word in the dictionary contains at least 1 and at most 10 lower-case characters.
The dictionary is sorted in lexicographically increasing order.
The dictionary does not contain duplicate words.
The total number of characters in the dictionary is 3323296.
S is valid: it is possible to make it using the method described above.
Small dataset (Test set 1 - Visible)
Time limit: 30 seconds.
1 ≤ T ≤ 20.
1 ≤ length of S ≤ 50.
Large dataset (Test set 2 - Hidden)
Time limit: 60 seconds.
1 ≤ T ≤ 4.
1 ≤ length of S ≤ 4000.
Sample
9 aabea bobs code in jam oo operation production system 4 codejam cxdejax cooperationaabea jobsinproduction
Case #1: 0 Case #2: 2 Case #3: 1 Case #4: 1
Explanation
"code" and "jam" both appear in the dictionary. Although "cooperation" is an English word, it doesn't appear in the dictionary; "aabea" does.
Note that to make the sample case visible in the problem statement, the size of the dictionary in the sample case does not satisfy the limits.
Analysis — A. Osmos
There is an optimal solution where Armin chooses to absorb motes in order from smallest to largest (skipping removed motes).
If Armin's solution absorbs mote X before mote Y, and mote X is larger than mote Y, then he could change his solution to absorb Y right before X, without needing to perform any extra "add" or "remove" operations. So if Armin has an optimal solution, we can always change it into an optimal solution that absorbs motes in order of size.
Now we can limit our search to solutions that absorb motes in order of size. We could use a dynamic programming algorithm where the state is the number of motes considered, and Armin's mote's current size or the number of operations performed, but there is a simpler algorithm based on the following observation:
In an optimal solution, if Armin removes a mote, he also removes all motes of equal or greater size.To see this, consider a solution where there exist motes X and Y where X is smaller than or equal in size to Y, X is removed, and Y is absorbed. X could instead be absorbed immediately before Y is absorbed, which would save an operation by not removing X. So the solution cannot be optimal.
So to find an optimal solution, we only need to consider N+1 cases -- those where we try to absorb 0, 1, ... N of the original motes and remove the remainder.
To find how many operations are needed for each of these cases, we simulate Armin trying to absorb each mote in turn. If Armin's mote is not yet large enough to absorb the next mote, we add motes of size one less than Armin's mote's current size and absorb them, until Armin's mote is large enough.
This solution takes O(N2) time to run as written, which is fast enough given the input size limits. There is a small adjustment to it that will make it linear, though. Can you see it?
One final case to handle is when Armin's mote is of size 1, and so is unable to absorb any motes at all. We were generous and added this as a case in the sample input!
This mechanics for this problem were inspired by Osmos by Hemisphere Games.
Analysis — B. Falling Diamonds
This was a tricky problem, and solving the small often made the difference between advancing and not - in particular, solving all of this problem was enough to advance; as was solving the small of this problem and the large of Osmos.
The small case
For the small case, we had only twenty diamonds to deal with in each test case. Note that every diamond will do something non-deterministic at most once, when it falls point down on the point of another diamond (when it can slide in one of two directions). This means that we will have at most 220 different things that can happen when the diamonds fall, so we can simply try to enumerate all of them (note that there is actually less possible paths - for instance the first, fifth and sixth will never have a choice).
This is actually a bit tricky to do, since in each branch we have to keep track of what is the probability of reaching this branch — it is not only dependent on how many diamonds we processed so far, but rather on how many diamonds had a choice so far. After this is done, we need to figure out in how many of all the options the place we're interested in did get a diamond and add them all up. All this is not easy to get right, but it is doable, as over 900 of our contestants proved!
The large case
For the large test case, we will need to be smarter — simulating all the options is obviously not a choice for 106 diamonds. We will begin with the following observation:
The diamonds fall in layers. First a diamond falls at (0, 0), then diamonds fall into positions with |X| + |Y| = 2, only after all five of these are filled the positions with |X| + |Y| = 4 start filling, only after them the |X| + |Y| = 6 start filling, and so on.Indeed, note that the diamond sliding to one side does not change the layer it is in, since it always starts sliding in some (0, 2k) position, and the (0, 2k) position is always the last in a layer to be filled.
Thus, when N diamonds fall, the only uncertainty as to how they shape up is in the last layer, and this is what we have to calculate. If the place we are considering is not in this layer, we can respond immediately. Thus, we have only to figure out probabilities in the last layer.
The dynamic programming approach
First let's estimate how large the last layer can be. If we have at most a million diamonds, one can calculate there will be no more than 710 layers. When diamonds fall, the state of the layer can be described by two numbers — how many diamonds are on the left of the center (with negative X), and how many are to the right (we assume here there aren't enough diamonds to fill this layer, so the top spot with X = 0 will stay empty). This means that when the diamonds drop, there are roughly 500,000 different states to consider.
One can approach to this problem is dynamic programming. For each of the states possible for the last layer, we calculate the probability of reaching this state when the appropriate number of diamonds has dropped (each state determines the number of diamonds uniquely).
A formulaic approach
One can also notice that what matters is how many diamonds of the ones that hit the top decide to go left, and how many to go right. Which diamonds exactly are those does not matter for the final state. Thus, we can precalculate binomial coefficients (or rather binomial coefficients divided by 2D, where D is the number of diamonds falling into the layer), and — once we know which layer we're looking — sum up the options that lead to a diamond falling into the right place.
Analysis — C. Garbled Email
There are multiple approaches possible to this problem. For the small test case, one can use a dynamic programming approach to calculate for each prefix of the given word what's the smallest number of substitutions needed to form this word so that the last substitution was k characters ago, for k = 1, 2, 3, ...
For example, for the word "codejam", we will find that "c" cannot be formed without a substitution, but can be formed (for instance from "a") by a substitution 1 character away. We find this by going over all dictionary words. Then, we go over all dictionary words to try and form "co" (we can do this, for instance, from "do" with one substitution 2 characters ago). We can also consider one letter words to extend the "c" we already know how to form, but this won't work, since "o" isn't a word, and we're too near to the last substitution. Next goes "cod", which actually is a word, so can be formed with zero subsitutions. Next goes "code" — for this we have a number of choice, like combining the "c" we know how to form and "ode", or the "cod" and a one substitution to form "e" from "a", or — the best one, since requiring no subsitutions — just using the word "code".
In this fashion for each prefix and each distance of the last substitution we can find out what's the least number of substitutions needed to form this prefix by looking at all smaller prefixes (including the empty one), all smaller dictionary words, and figuring out whether we can combine them.
For the large test case, we can't afford to go over the whole dictionary that often. So, we start by building a hash table. For each dictionary word, we insert that word into the hash table, and also insert the word with each possible set of changed letters in the word replaced by '*' characters.
For example, for the word "coders", we store in the hash table:
coders*odersc*dersco*erscod*rscode*scoder**oder*
Each of the states where this is possible corresponds to a partial solution. We consider each possible way of adding one more word to create a longer partial solution. To do this, we try each combination of:
- The length of the next word, L (1 ≤ L ≤ 10).
- Each possible set of positions of changed letters in the next word, S.
The answer is the minimum number of changes found to produce the prefix that is the entire email.