Google Code Jam Archive — World Finals 2012 problems
Overview
The final round of Google Code Jam 2012 was hard-fought throughout, and suspenseful at its end. In a round where contestants were faced with two medium-difficulty problems and three very tough ones, the careful choice of which problems to attack was vital.
The contest for the highest ranks would come down to the very end. Six of the top eight contestants would make submissions in the last ten minutes of the four-hour contest, and three of them would earn points off of those submissions. At the end of the round, the scoreboard was as clear as mud: most of the points would come from Large submissions, and over ten of those would prove to be wrong.
The dust settled on a close scoreboard, whose final ordering came down to the problems contestants chose to solve and to the time it took them. In third place was Slovakia's misof, who solved C and earned partial points for D and E. In second, with his final submission to D coming seven minutes before the end of the contest, was the USA's neal.wu. The winner, with the same problems and a time nearly an hour and a half faster, was Poland's meret. He claims the title of Code Jam Champion, as well as a cool $10,000.
That's it for Google Code Jam 2012! With that exciting sendoff, we're really looking forward to seeing you all again in 2013.
Cast
Problem A. Zombie Smash Written by Andrei Missine. Prepared by Greg Tener and Andrei Missine.
Problem B. Upstairs/Downstairs Written by Bartholomew Furrow, with Petr Mitrichev and David Arthur. Prepared by John Dethridge and Bartholomew Furrow.
Problem C. Xeno-archaeology Written by David Arthur. Prepared by Onufry Wojtaszczyk and Igor Naverniouk.
Problem D. Twirling Towards Freedom Written by David Arthur. Prepared by Luka Kalinovcic and Igor Naverniouk.
Problem E. Shifting Paths Written and prepared by David Arthur.
Contest analysis presented by Bartholomew Furrow, Andrei Missine, Bartholomew Furrow, Onufry Wojtaszczyk, John Dethridge and David Arthur.
Solutions and other problem preparation provided by Adam Polak, Anton Georgiev, Irvan Jahja, Khaled Hafez, Mark Gordon, Nikolay Kurtov, Steve Thomas and Raymond Ho. Fun fact: David Arthur writes hard problems.
A. Zombie Smash
Problem
You are playing Zombie Smash: a game where the objective is to smash zombies with your trusty Zombie Smasher as they pop out of graves at the graveyard. The graveyard is represented by a flat 2D grid. Each zombie will pop out of a grave at some (X, Y) cell on the grid, stand in place for 1000 milliseconds (ms), and then disappear back into the grave. At most one zombie can stand around a grave at a time.
You can move to any one of the 8 cells adjacent to your location in 100ms; i.e., you can move North, East, South, West, NW, NE, SW, and SE of your current location. You may move through or stand on a cell even if it is currently occupied by a zombie. You can smash a zombie instantly once you reach the cell that the zombie is standing on, but once you smash a zombie it takes 750ms for your Zombie Smasher to recharge before you can smash another zombie. You may move around while Zombie Smasher is recharging. For example, immediately after smashing a zombie at (0, 0):
- It will take 750ms to reach and smash a zombie at (1, 1) or
- 2000ms to reach and smash a zombie at (20, 20).
You start at cell (0, 0) at the beginning of the game (time=0). After you play a level you would like to know how many zombies you could have smashed, if you had played optimally.
Input
The first line will contain a single integer T, the number of test cases. It is followed by T test cases, each starting with a line containing a single integer Z, the number of zombies in the level.
The next Z lines contain 3 space-separated integers each, representing the location and time at which a given zombie will appear and disappear. The ith line will contain the integers Xi, Yi and Mi, where:
- Xi is the X coordinate of the cell at which zombie
iappears, - Yi is the Y coordinate of the cell at which zombie
iappears, - Mi is the time at which zombie
iappears, in milliseconds after the beginning of the game. The time interval during which the zombie can smashed is inclusive: if you reach the cell at any time in the range [Mi, Mi + 1000] with a charged Zombie Smasher, you can smash the zombie in that cell.
Output
For each test case, output one line containing "Case #c: d", where c is the case number (starting from 1), and d is the maximum number of zombies you could have smashed in this level.
Limits
Memory limit: 1GB.
Time limit: 30 seconds per test set.
1 ≤ T ≤ 100.
-1000 ≤ Xi, Yi ≤ 1000.
0 ≤ Mi ≤ 100000000 = 108.
Two zombies will never be in the same location at the same time. In other words, if one zombie appears at (x, y) at time t, then any other zombie that appears at (x, y) must appear at or before (t - 1001), or at or after (t + 1001).
Test set 1 (Visible Verdict)
1 ≤ Z ≤ 8.
Test set 2 (Hidden Verdict)
1 ≤ Z ≤ 100.
Sample
3 4 1 0 0 -1 0 0 10 10 1000 10 -10 1000 3 1 1 0 2 2 0 3 3 0 5 10 10 1000 -10 10 1000 10 -10 1000 -10 -10 1000 20 20 2000
Case #1: 3 Case #2: 2 Case #3: 2
B. Upstairs/Downstairs
Problem
Konstantin and Ilia live in the same house. Konstantin lives upstairs, and enjoys activities that involve jumping, moving furniture around, and - in general - making noise. Ilia lives downstairs, and enjoys sleep.
In order to have a good evening, Konstantin wants to do at least K activities. Last night, Ilia asked Konstantin to try not to wake him up; and because Konstantin is a very nice neighbor, he agreed. Unfortunately, he took Ilia's request a bit too literally, and he will choose his activities in such a way as to minimize the probability that Ilia is woken up after falling asleep.
Each possible activity for Konstantin has an associated probability ai/bi. If Konstantin performs this activity, then at the end of it, Ilia will be awake with probability ai/bi, and asleep otherwise, regardless of whether he was asleep at the start. Moreover, for each possible activity Konstantin can perform it at most ci times (more than that would be boring, and Konstantin won't have a good evening if he's bored).
Konstantin wants to choose a number of activities to do, in order, so that:
- The total number of activities done is at least K.
- The ith activity is performed no more than ci times.
- The probability Q that Ilia is woken up one or more times during the course of the activities is as small as possible.
What is the smallest Q Konstantin can achieve while having a good evening? Note that Konstantin cannot tell whether Ilia is awake or asleep, and so he cannot adapt his activities using that information.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case starts with a pair of integers, N, K, on a line by themselves. N lines follow, each of which represents an activity that Konstantin can choose. Each of those lines is formatted as "ai/bi ci", indicating that there is an activity which would leave Ilia awake with probability ai/bi and which Konstantin can perform at most ci times without being bored.
Output
For each test case, output one line containing "Case #x: Q", where x is the case number (starting from 1) and Q is the smallest probability of Ilia waking up during the course of the activities that Konstantin performs. Answers with absolute or relative error no larger than 10-6 will be accepted.
Limits
Memory limit: 1GB.
1 ≤ T ≤ 100.
0 ≤ ai ≤ bi ≤ 1000000 for all i.
1 ≤ bi and 1 ≤ ci for all i.
1 ≤ K ≤ the sum of all ci in that test case.
Test set 1 (Visible Verdict)
Time limit: 30 seconds.
1 ≤ N ≤ 100.
The sum of all ci is no larger than 100 in each test case.
Test set 2 (Hidden Verdict)
Time limit: 60 seconds.
1 ≤ N ≤ 10000.
The sum of all ci is no larger than 106 in each test case.
Sample
3 4 1 1/2 3 1/5 2 2/5 1 2/2 2 3 2 1/2 2 1/3 2 3/4 2 3 3 99/100 1 1/2 2 1/50 3
Case #1: 0.000000000 Case #2: 0.083333333 Case #3: 0.015000000
C. Xeno-archaeology
Problem
Long ago, an alien civilization built a giant monument. The floor of the monument looked like this:
############### #.............# #.###########.# #.#.........#.# #.#.#######.#.# #.#.#.....#.#.# #.#.#.###.#.#.# #.#.#.#.#.#.#.# #.#.#.###.#.#.# #.#.#.....#.#.# #.#.#######.#.# #.#.........#.# #.###########.# #.............# ###############Each '#' represents a red tile, and each '.' represents a blue tile. The pattern went on for miles and miles (you may, for the purposes of the problem, assume it was infinite). Today, only a few of the tiles remain. The rest have been damaged by methane rain and dust storms. Given the locations and colours of the remaining tiles, can you find the center of the pattern?
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each one starts with a line containing N, the number of remaining tiles. The next N lines each contain Xi, Yi, and the tile colour (either '#' or '.').
Output
For each test case, output one line containing
Limits
Memory limit: 1GB.
Time limit: 30 seconds per test set.
1 ≤ T ≤ 50.
The list of coordinates in each test case will not contain duplicates.
Test set 1 (Visible Verdict)
1 ≤ N ≤ 100.
-100 ≤ Xi ≤ 100.
-100 ≤ Yi ≤ 100.
Test set 2 (Hidden Verdict)
1 ≤ N ≤ 1000.
-1015 ≤ Xi ≤ 1015.
-1015 ≤ Yi ≤ 1015.
Sample
6 1 0 0 . 1 0 0 # 3 0 0 # 0 1 # 1 0 # 5 50 30 # 49 30 # 49 31 # 49 32 # 50 32 # 2 -98 0 # 99 50 . 4 88 88 . 88 89 . 89 88 . 89 89 .
Case #1: 0 0 Case #2: 1 0 Case #3: 1 1 Case #4: 50 31 Case #5: 1 0 Case #6: Too damaged
D. Twirling Towards Freedom
Problem
"I say we must move forward, not backward;
upward, not forward;
and always twirling, twirling, twirling towards freedom!"
— Former U.S. Presidential nominee Kodos.
After hearing this inspirational quote from America's first presidential nominee from the planet Rigel VII, you have decided that you too would like to twirl (rotate) towards freedom. For the purposes of this problem, you can think of "freedom" as being as far away from your starting location as possible.
The galaxy is a two-dimensional plane. Your space ship starts at the origin, position
How far away can you move from the origin after M minutes?
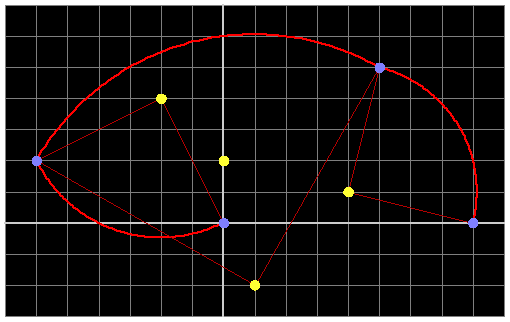
The image illustrates the first 3 rotations for a possible path in sample case 1. Note that this path is not necessarily a part of any optimal solution.
Input
The first line of the input gives the number of test cases, T. T test cases follow, beginning with two lines containing integers N and M. The next N lines each contain two integers, Xi and Yi, representing the locations of stars.
Output
For each test case, output one line containing "Case #x: D", where x is the case number (starting from 1) and D is the distance from the origin to the optimal final position. Answers with absolute or relative error no larger than 10-6 will be accepted.
Limits
Memory limit: 1GB.
1 ≤ T ≤ 100;
-1000 ≤ Xi ≤ 1000;
-1000 ≤ Yi ≤ 1000.
No two stars will be at the same location.
There may be a star at the origin.
Test set 1 (Visible Verdict)
Time limit: 30 seconds.
1 ≤ N ≤ 10.
1 ≤ M ≤ 10.
Test set 2 (Hidden Verdict)
Time limit: 60 seconds.
1 ≤ N ≤ 5000.
1 ≤ M ≤ 108.
Sample
3 4 1 -2 4 1 -2 4 1 0 2 1 4 -5 0 2 5 -1 1 -2 2
Case #1: 6.3245553203 Case #2: 10.0000000000 Case #3: 6.3245553203
E. Shifting Paths
Problem
You have been walking in the woods for hours, and you want to go home.
The woods contain N clearings labeled 1, 2, ..., N. You are now at clearing 1, and you must reach clearing N in order to leave the woods. Each clearing from 1 to N-1 has a left path and a right path leading out to other clearings, as well as some number of one-way paths leading in. Unfortunately, the woods are haunted, and any time you enter a clearing, one of the two outgoing paths will be blocked by shifty trees. More precisely, on your kth visit to any single clearing:
- You must leave along the left path if k is odd.
- You must leave along the right path if k is even.
- All paths are one-way, so you have no choice at each step: you must go forward through the one unblocked outgoing path.
You begin at clearing #1, and when you get to clearing #N, you can leave the woods. How many paths do you need to follow before you get out?
Input
The first line of the input gives the number of test cases, T. T test cases follow, each beginning with a line containing a single integer N.
N-1 lines follow, each containing two integers Li and Ri. Here, Li represents the clearing you would end up at if you follow the left path out of clearing i, and Ri represents the clearing you would end up at if you follow the right path out of clearing i.
No paths are specified for clearing N because once you get there, you are finished.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is the number of paths you need to follow to get to clearing N. If you will never get to clearing N, output "Infinity" instead.
Limits
Memory limit: 1GB.
Time limit: 30 seconds per test set.
1 ≤ T ≤ 30.
1 ≤ Li, Ri ≤ N for all i.
Test set 1 (Visible Verdict)
2 ≤ N ≤ 10.
Test set 2 (Hidden Verdict)
2 ≤ N ≤ 40.
Sample
2 4 2 1 3 1 2 4 3 2 2 1 2
Case #1: 8 Case #2: Infinity
Sample Explanation
In the first sample case, your route through the woods will be as shown below:
| Paths followed | Clearing | Path direction |
| 0 | 1 | Left |
| 1 | 2 | Left |
| 2 | 3 | Left |
| 3 | 2 | Right |
| 4 | 1 | Right |
| 5 | 1 | Left |
| 6 | 2 | Left |
| 7 | 3 | Right |
| 8 | 4 | - |
Analysis — A. Zombie Smash
Firstly, it is worth noting that the small dataset with only 8 zombies can be solved simply by evaluating each possible permutation for the order in which to smash zombies and keeping the best one. For each permutation, simply attempt to smash the zombies in the order given, skipping any zombies that cannot be reached on time. This simple approach has exponential time complexity and clearly will not scale for the large data set.
For the more efficient approach, let us start by considering the game state represented in an inefficient way and see how it can be made more efficient. We can represent the game state at any point in time with the following tuple:
- (Time, Location, Set of zombies already smashed)
- (Time last zombie was smashed, Last zombie smashed, Set of zombies already smashed)
Consider the state (T1, Z1, {Z1 …}) where we have just smashed zombie Z1 at time T1. The set of zombies already smashed contains Z1, and possibly a bunch of other zombies. Suppose that Z0 is a zombie that we have smashed earlier. There are two cases: either Z0 appears at an interval overlapping with Z1, or it has already appeared before Z1.
- If Z0 has already appeared before Z1 then by T1 it can no longer be at its grave (even if we haven’t smashed it) and explicitly tracking that it has already been smashed is unnecessary.
- Otherwise, if Z0 appears in an interval overlapping with Z1, is it possible that we will attempt to smash Z0 again, if we don’t keep track of it? Suppose that Z0 was smashed at T0, since the Zombie Smasher needs to recharge twice, Z0 will be already gone because it stands around for 1000ms and it takes 1500ms for the Zombie Smasher to recharge twice. Again, it is not necessary to explicitly track the set of zombies smashed to avoid smashing the same zombie twice.
In light of the above observations we can simplify the state to be:
- (Time last zombie was smashed, Last zombie smashed, Number of zombies already smashed)
The game starts at time 0 and location (0, 0). Based on this information, we can generate the initial frontier of zombies that can be reached and smashed on time. Given this frontier, the times and the locations at which zombies will appear, we can apply a modified Dijkstra’s Algorithm to find the set of game states that are reachable. Once we know those, we can simply return the maximum number of zombies smashed in a reachable state. Here is the pseudo-code:
solve():
all_states = Q = generateStates()
while Q is not empty:
s = Q.popMin()
if s.time = infinity:
break;
for each zombie z such that z ≠ s.zombie:
earliest_arrival_time = s.time + max(750,
dist(s.zombie, z))
if earliest_arrival_time ≤ z.appearance + 1000:
earliest_smash_time = max(z.appearance,
earliest_arrival_time)
Q.update(earliest_smash_time, z, s.smashed + 1)
// Scan for states with time < infinity, keeping the maximum
// number of zombies smashed to get the final answer.
return best_reachable_state(all_states)
generateStates():
states = {}
states.Add(0, nil, 0) // Include the initial state.
for each zombie z:
for zombies_killed from 1 to Z:
// For other reachable states this will be revised later.
earliest_smash_time = infinity
if zombiles_killed = 1:
earliest_arrival_time = dist((0, 0), z)
if earliest_arrival_time ≤ z.appearance + 1000:
earliest_smash_time = max(z.appearance,
earliest_arrival_time)
states.Add(earliest_smash_time, z, zombies_killed)
return states
Crude worst-case complexity analysis of the above: generateStates() will produce O(Z2) states as each element of the pair (Last zombie smashed, Number of zombies already smashed) can vary from 0 to Z independently. Each state will be iterated over at most once by the outer while loop of solve(), and the inner for loop of solve() will run over all zombies, costing another O(Z), assuming an efficient heap is used, giving O(Z3), which is fast enough for the large dataset where Z = 100. Lastly, a few contestants solved this problem with dynamic programming, keeping a 2D table with zombie index in one dimension and time since that zombie has popped up in the other dimension, maximizing on the total number of zombies smashed.
Analysis — B. Upstairs/Downstairs
Upstairs/Downstairs was a last-minute addition to the Finals, replacing a year-old problem proposal that had appeared on a separate contest two months before. This problem loosely mirrors an experience the author had once while on vacation. He was downstairs.
Solving this problem involves two observations and an algorithm. Before making our observations, let's start by writing out the formula for the quantity we want to minimize. pi will represent the probability that the ith activity Konstantin performs will result in Ilia being awake:
P(woken up) =
(1-p0) * (1 - (1-p1)(1-p2)*...* (1 - pK)) +
p0(1-p1) * (1 - (1-p2)(1-p3)*...*(1 - pK)) +
p0p1(1-p2) * (1 - (1-p3)(1-p4)*...*(1 - pK)) +
...
Observation 1: Noisy First
For our first observation, we'll look for a reason to prefer that Konstantin perform noisier or quieter activities earlier. Intuitively, we suspect that noisier activities should come first: a strategy that keeps Ilia awake and then tries to keep him asleep seems pretty reasonable.
Looking at the structure of the formula above, we can look for differences between how pi and pi+1 are used. Here are the terms in which swapping them would lead to a difference in the final result:
p0p1...pi-1(1-pi) * (1 - (1-pi+1)(1-pi+2)*...*(1 - pK)) +
Simplifying these two terms, we have:
p0p1...pi-1pi(1-pi+1) * (1 - (1-pi+2)*...*(1 - pK))
p0p1...pi-1 * [
This quantity is minimized by choosing
(1-pi) + pi(1-pi+1) -
(1-pi)(1-pi+1)...(1-pK) -
pi(1-pi+1)...(1-pK)]
= p0p1...pi-1 * [1 - pipi+1 - (1 - pi+1)(1 - pi+2)...(1 - pK)]
pi+1 < pi, which confirms the intuition that noisier activities should happen earlier. Repeatedly swapping adjacent activities like this shows that in an optimal solution, activities should be performed from noisiest to quietest.
Observation 2: Go Extreme!
Our original formula for P(woken up) is clearly linear in pi for all i. This quantity therefore must be minimized by taking either the largest possible value or the smallest possible value for pi.
Putting this observation together with the previous one, we can conclude that Konstantin should start by performing the K-q noisiest activities in order from noisiest to quietest, and then should perform the q quietest activities, also in order from noisiest to quietest. We'll call the first set of activities the prefix, and the others the suffix. Note that here we're considering an activity that can be repeated c times as c different activities.
Possible Algorithms
For the Small, it's sufficient to try all values of q. There are O(K) possible values, and evaluating each one naively takes O(sum(ci)) time, so the running time is O(sum(ci)2).
There are only two numbers we really need to keep track of for each possible suffix: the probability that Ilia will end up being woken up if he starts the suffix awake, and the probability that he will end up being woken up if he starts the suffix asleep. After precomputing those 2 values for each of the K possible suffixes, which we can do in O(K) time, we can simulate each possible prefix, also in O(K) time, and do a quick lookup for the corresponding suffix for each one. A little math produces the correct answer, in O(sum(ci)) time.
Another algorithm that boils down to the same thing involves treating Ilia's three states—awake, asleep, and woken up—as a 3x1 vector that can be operated on by matrices. For any activity, we can build a 3x3 transition matrix, looking like this:
[[p 0 0] [1-p 1-p 0] [0 p 1]]Ilia's initial state is:
[1 0 0]To build the transition matrix for a series of activities, we can multiply the activities' matrices together, with the noisiest activity on the right. In this way, we can compute a 3x3 matrix corresponding to each prefix of length up to K, and one for each suffix of length up to K, in
O(K) time. Then it's an O(1) operation to check the result for any given prefix/suffix pair: multiplying those two matrices by each other, then by Ilia's initial state. The algorithm ends up taking O(sum(ci)) time.
Note that the bolded entries of the transition matrix, above, correspond to the two numbers we cared about for each suffix in the previous algorithm.
Ternary Search Passed Test Cases, But...
Because this problem was prepared at the last minute, it didn't occur to us until during the contest to wonder whether ternary search would work for selecting q, the length of the suffix. We would have been happy with the answer either way, but we would have wanted test data that would break ternary search if the answer turned out to be "no".
It turned out that the answer was "no", and that none of our existing cases broke any ternary search that we found. Because of this, some contestants—most notably misof, who came third partly on the strength of the points he got from this problem—managed to submit ternary search solutions that passed our test data.
Sometimes it happens in Code Jam that contestants will come up with algorithms that don't work in general given the limits we've provided, but do work on our test data. We try to avoid situations of that sort, but they do happen. We think the consequences here weren't significant, for a few reasons: Implementing the ternary search is about as hard as implementing a correct solution, if not a little harder; the "hard part" of the problem was already done by that point; and if we'd come up with a breaking case, we'd have put it in the Small data as well as the Large. Contestants who implemented ternary search would have seen it was wrong in the Small, and taken the time to fix it. misof had plenty of time separating him from the fourth-place contestant, so the top three likely would not have changed.
Why Ternary Search Fails
Ternary search seems like it should work. Indeed, the function that we're minimizing, P(woken up), is strictly non-increasing and then strictly non-decreasing in q. Unfortunately, that isn't quite enough: it needs to be strictly decreasing and then strictly increasing; otherwise a large constant patch will leave the ternary search unable to tell which direction it should go in.
Here's an example case that breaks ternary search in principle, and breaks a few contestants' submissions in practice:
2
2 200
1/2 40
1/100 400
2 200
1/2 40
99/100 400
The correct answer is:
Case #1: 0.863976521
Case #2: 0.863976521
In the first case, the "1/2" activities are best not performed; but because they are at the very start of the list of activities, outnumbered severely by the "1/100" activities, a standard ternary search will find no difference between the two suffix lengths it tries. It will merely consider a different number of "1/100" activities to be part of the suffix as opposed to the prefix, and leave all the "1/2" activities in place. The second case is identical, but with "99/100" activities instead of "1/100" activities, which should defeat a ternary search that happens to choose the right direction in the first case.
Paweł i Gaweł
At dinner after the finals, several Polish contestants were shocked to discover that the problem was not based on a poem called Paweł i Gaweł. The similarity was entirely coincidental, as the contestants should have known: Gaweł, who (according to Google Translate's translation of that page) "invented the wildest frolics", lived downstairs. Still, in retrospect, we wish we'd named the problem after that poem, and perhaps had Gaweł minimize the probability that Paweł would go fishing.
Analysis — C. Xeno-archaeology
To begin with, let's try to formalize the rules of forming the pattern of tiles. If the center is at some position x, y, then the red tiles are those in positions x', y' for which the number max(|x - x'|, |y - y'|) is odd, while the blue tiles are those for which this number is even. This is because the formula max(|x - x'|, |y - y'|) = C for any C describes a square ring around x, y, and the rings alternate color with the parity of C
For the small problem, we can prove that if there exists a solution, there exists one with |X| + |Y| < 202. Thus, we can check all candidates for the center, for each one check whether all the tiles have the right colors, and output the best candidate. This will not run in time for the large data, of course, as we will have over 1030 candidate centers to check.
Single tile analysis
We may now assume we know the parity of x and y. We will simply check all four possibilities, finding the best possible choice of the center for each of the four assumptions, and then pick the one specified by the tie-breaking rules (or output "Too damaged" if none of the four assumptions led to finding a viable center for the pattern). This makes it easier to analyse the information gained by knowing the color of a single tile. Suppose the tile at some position x', y' is, say, red. This means max(|x - x'|, |y - y'|) has to be odd. Now, we know the parities of x, y, x' and y', and so:
- if both x - x' and y - y' are odd, then any choice of a center (satisfying the parity requirements for x and y) is going to fit our knowledge;
- if both x - x' and y - y' are even, then there is no solution satifying the parity requirements;
- if, say, x - x' is odd, while y - y' is even, we have to have |x - x'| ≥ |y - y'|
Note that in the third case, since the parities of x - x' and y - y' differ, it doesn't matter whether we use a strict inequality, as the equality case is eliminated from consideration by the parity assumptions. Thus, when considering regions defined by these inequalities, we can ignore problems related to "what happens on the edges of these regions", as - by the reasoning above - the edges will necessarily be eliminated from consideration by the parity assumptions.
The first and second cases are easy to analyse; the trick is to find out whether a solution exists (and if yes, find the best one) satisfying the set of conditions of the type |x - x'| ≥/≤ |y - y'| for various x' and y'. Transforming the condition |x - x'| ≥ |y - y'| we see it is equivalent to saying that one of the following has to hold:
- x + y ≥ x' + y' and x - y ≥ x' - y', or
- x + y ≤ x' + y' and x - y ≤ x' - y'.
Dividing the plane
The lines x + y = xi + yi and x - y = xi - yi (which are the boundaries of the constraint-satisfaction region for the input tiles) divide the plane into at most (N + 1)2 rectangles. The idea of our algorithm will be as follows:
- Iterate over the four sets of parity assumptions about the center
- Iterate over all rectangles formed by the boundary lines, and for each of them check whether it satisfies the constraints posed by all input tiles
- for each rectangle satisfying the constraints, find the best (according to the tie-resolution conditions) center candidate within it (if any)
- output the best of all center candidates found.
There are many ways to trim down the runtime of the constraint-checking phase for rectangles. One sample way is to process the rectangles "row-by-row", as follows: Take the set of rectangles with A ≤ x+y ≤ B, with A and B being some two adjacent boundary values. For each input tile (out of those that set any constraints on the center position), we have two areas of constraint satisfaction; but only one of them is compatible with A ≤ x+y ≤ B, because one of the areas satisfies the constraint x+y ≥ C, while the other has x+y ≤ C. This means that we know which area is the interesting one for this row; so we obtain a constraint on x - y that has to be satisfied by all the rectangles in this row. This will be either of the form x - y ≤ D, or x - y ≥ D. We take the largest of the lower bounds, the largest of the upper bounds, and obtain a rectangle that we have to check. This algorithm runs in O(N2) time, which will be easily fast enough.
A more advanced algorithm (using the sweep line technique) can be used to obtain a runtime of O(N logN) runtime. We will not describe it (as it is not necessary to obtain a fast enough program with the constraints given), but we encourage the reader to figure it out.
Finding the best point within a rectangle
This was the part of the problem that seemed to cause most difficulties for our contestants. There are two cases to consider here. Let's assume our rectangle is defined by A ≤ x+y ≤ B and C ≤ x-y ≤ D.
Let us define
g(k, l) = min(|k|, |l|) if k and l are of the same sign, 0 otherwise.
If g(A, B) = 0 and g(C, D) = 0, then the point (0, 0) is within our rectangle. In this case it suffices to check the near vicinity of the origin. Specifically:
- If both x and y are supposed to be even, (0, 0) is obviously the optimal solution.
- If both x and y are supposed to be odd, then the best four points, in order, are (1, 1), (1, -1), (-1, 1) and (-1, -1). If B ≥ 2 we can take (1, 1) and we're done. Otherwise, if D ≥ 2, we take (1, -1); and so on. If all the four points are infeasible, the rectangle contains no points satisfying the parity constraints.
- If , say, x is supposed to be odd, while y is even, the first eight candidates are (1, 0), (-1, 0), (3, 0), (1, 2), (1, -2), (-1, 2), (-1, -2), (-3, 0). Again, one can check that if none of them is feasible, the rectangle contains no points satisfying the parity constraints. The same happens when x is even and y is odd.
When (0, 0) is not within the rectangle, we first look for the smallest Manhattan distance of any point within the rectangle. It is equal to M := max(g(A, B), g(C, D)). As all the boundaries have parities disagreeing with the parity assumptions, the smallest Manhattan distance we can hope for is M + 1. We now have an interval of points with Manhattan distance M + 1 in our rectangle, the best one of them is the one with the highest X coordinate (out of the ones fulfilling the parity conditions). The one last special case to deal with here is when the interval contains only one point, and it has the wrong parities - in this case we need to look at distance M + 3 (the fact that one never needs to look at M + 5 is left as an exercise).
It was also possible to solve this problem in a number of other ways. A pretty standard one was to identify a number of "suspicious points" within a rectangle (the vicinity of (0, 0), the vicinity of the corners, and the vicinity of places where the coordinate axes intersect the edges of the rectangle) and check them all, taking the best solution.
Analysis — D. Twirling Towards Freedom
The Small Input
On most Google Code Jam problems, the small input can be solved without worrying about the running time. That was not the case here though. Even if N = 10 and M = 10, there are still 1010 different rotation patterns you could try. That is a lot!
There are various ways you could try to bring the running time down to a more manageable amount, but here is one fact that makes it easy:
- The 1st star you rotate around, the 5th star you rotate around, and the 9th star you rotate around should all be the same.
- The 2nd star you rotate around, the 6th star you rotate around, and the 10th star you rotate around should all be the same.
- The 3rd star you rotate around and the 7th star you rotate around should be the same.
- The 4th star you rotate around and the 8th star you rotate around should be the same.
Understanding Rotations
One of the biggest challenges here is just wrapping your head around the problem. How can you intuitively understand what it means to rotate something 100,000 times? The best way to do this is to roll up your sleeves and write down a couple formulas.
When dealing with rotations and translations of points on a plane, complex numbers provide an excellent notation:
- A point (x, y) can be represented as x + iy.
- Complex numbers can be added and subtracted just like vectors.
- Complex numbers can be rotated clockwise 90 degrees about the origin simply by multiplying them by -i.
We know that rotating a point P0 by 90 degrees about the origin will send it to -i * P0. However, what happens if we rotate it about a different point Q0? There is a standard formula for this situation that you may have already seen. The resulting point P1 satisfies the following:
P1 - Q0 = -i * (P0 - Q0)
This is our previous formula applied to the fact that rotating P0 - Q0 by 90 degrees about the origin must give you P1 - Q0. (Do you see why that is true? It's really just a coordinate change.) In our case, it will be helpful to group things a little differently in the formula:
P1 = -iP0 + Q0 * (1 - i)
Now, suppose we rotate P1 by 90 degrees about another point Q1, then by 90 degrees about another point Q2, and so on. What would happen to this formula? Let's write out a few examples:
- P2 = -iP1 + Q1 * (1 - i) = -P0 + Q1 * (1 - i) + Q0 * (-1 - i).
- P3 = -iP2 + Q2 * (1 - i) = iP0 + Q2 * (1 - i) + Q1 * (-1 - i) + Q0 * (-1 + i).
- P4 = -iP3 + Q3 * (1 - i) = P0 + Q3 * (1 - i) + Q2 * (-1 - i) + Q1 * (-1 + i) + Q0 * (1 + i).
- P5 = -iP4 + Q4 * (1 - i) = -iP0 + (Q4 + Q0) * (1 - i) + Q3 * (-1 - i) + Q2 * (-1 + i) + Q1 * (1 + i).
- etc.
From here, it's not too hard to guess the general formula. If the origin is rotated by 90 degrees about Q0, then Q1, and so on, all the way through Qm-1, then the final resulting point Pm is given by:
(1 - i) * (Qm-1 + Qm-5 + Qm-9 + ...) + (-1 - i) * (Qm-2 + Qm-6 + Qm-10 + ...) + (-1 + i) * (Qm-3 + Qm-7 + Qm-11 + ...) + (1 + i) * (Qm-4 + Qm-8 + Qm-12 + ...)
And once the formula is written down, it's not too hard to check that it always works. So anyway, is this simpler than the original problem formulation? It may look pretty complicated, but for the most part, you're now just adding points together here, and addition is easier than rotation!
Pick a Direction
We want to choose stars Q0, Q1, ..., Qm-1 in such a way as to make the following point as far away from the origin as possible:
(1 - i) * (Qm-1 + Qm-5 + Qm-9 + ...) + (-1 - i) * (Qm-2 + Qm-6 + Qm-10 + ...) + (-1 + i) * (Qm-3 + Qm-7 + Qm-11 + ...) + (1 + i) * (Qm-4 + Qm-8 + Qm-12 + ...)
There are different ways of thinking about things from here, but the key is always convex hulls.
Let X be the point furthest from the origin that we can attain, and more generally, let Xv be the point that is furthest in the direction of v that we can attain. Certainly, X = Xv for some v. (This is because X is surely the point that is furthest in the direction of X.) Therefore, it suffices to calculate Xv for all v, and we can then measure which of these is furthest from the origin to get our final answer.
So how do we calculate Xv for some given v? We want (1 - i) * Qm-1 to be as far as possible in the v direction, or equivalently, we want Qm-1 to be the star that is furthest in the (1 + i)*v direction. Of course, the same thing is true for Qm-5, Qm-9, etc. We should choose the same star for all of them. (This is the fact that we used for the small input solution!) Similarly, for Qm-2, Qm-6, etc., we want to choose the star is furthest in the (-1 + i)*v direction. In general, we want to choose stars from the original set that are as far as possible in the following directions: (1 + i)*v, (-1 + i)*v, (-1 - i)*v, (1 - i)*v.
We are now almost done (at least conceptually). First we find the convex hull of the stars and solve for one particular v. Now what happens when we rotate v? For a while, nothing will change, but eventually, one of the four directions we are trying to optimize will be perpendicular to an edge of the convex hull, and as a result, the optimal star will switch to the next point on the convex hull. This simulation can be done in constant time at each step, and there will be only O(N) steps since each star choice will rotate once around the convex hull.
At this point, we are done! We have found every Xv, and we can manually check each of them to see which one is best. The implementation here is tricky, but it is an example of a general technique called rotating calipers. You can find plenty more examples of it online. Or you can always download solutions from our finalists!
Bonus Question!
When we generated test data for this problem, we were surprised to find that we could not come up with a case to break solutions which misread "clockwise" as "counter-clockwise" in the problem statement. In fact, there is no such case! Can you see why?
Analysis — E. Shifting Paths
For the small dataset, we can directly simulate the process of walking through the forest. How many steps can this take? There are 210 states the trees in the clearings can be in, and 10 possible states for the clearing we are standing in. So if we reach the final clearing, it can't take more than 10 × 210 steps, and if we take that many steps without reaching the final clearing we know the answer is Infinity.
For the large dataset, 40 × 240 steps is too many to simulate directly, but can an input case approach this many?
A test case can be designed to make the clearings simulate an N-1 bit counter. The first clearing has both paths leading to the second clearing. Each clearing after that forms a chain where one path leads to the next clearing, and one path leads back to the first clearing. Whenever the trail leads back to the first clearing, the states of the clearings give the next N-1 bit number, and after all of those numbers have been produced, it can reach the final clearing. This will take at least 239 steps.
So we need a solution that will not simulate every step individually. In the previous example, we spend 221-2 steps in the first 20 clearings between each time we visit any of the last 20 clearings. If our program could detect that this always happens, it could simulate those 221-2 steps without having to do them all individually. We will only take 220-3 steps from any of the second twenty clearings, so the total runtime would be reasonable.
An implementation of this approach is to split the clearings into two sets A and B of roughly equal size. We then use dynamic programming to compute, for each location in A and each of the 2|A| states of the clearings in A, how many steps it will take to leave A, which clearing in B we will be leaving towards, and what state the clearings in A will be left in.
After this DP is done, our solution will take an amount of time proportional to the number of steps we take from clearings in B -- for each of those, we simulate that step, and if that takes us to a clearing in A, we look up the appropriate result of the DP from a table. So to make this solution efficient, we need to choose A and B so that only a small number of steps are taken from clearings in B.
Find the distance from each clearing to the final clearing, where distance is defined as the number of paths you need to take, assuming the state of the clearings is optimal. If the final clearing cannot be reached from some clearings, put those in a separate set. If we ever reach one of those, the answer is Infinity.
Choose B to be the closest half of the remaining clearings. There can be at most B × 2|B| steps taken from clearings in B, because we cannot repeat a state of B without reaching the final clearing. This can be only at most 20 × 220, so this solution is sufficiently fast.