Google Code Jam Archive — Round 2 2012 problems
Overview
Round 2 whittled down our field from 3000 to 500 contestants with a combination of very challenging problems. A theme in this round was the freedom to choose one of several ways to solve most of the problems we posed.
We began the round with a graph traversal problem that required one of a few possible insights to make it fast enough for the large input. This didn't stop 1630 of our contestants, though.
Aerobics is one of the problems that can be solved in very many ways, from rather grueling circle geometry to a nifty randomized solution requiring very little code. Next came Mountain View, an ad-hoc problem which required contestants to re-create an input that would match the provided output.
Finally came Descending in the Dark, a very challenging problem in which many contestants succumbed to the temptation of trying a randomized or heuristic solution. No one managed to solve the Large version of it, which was a very challenging DP!
Cast
Problem A. Swinging Wild Written by Onufry Wojtaszczyk. Prepared by Luka Kalinovcic and Onufry Wojtaszczyk.
Problem B. Aerobics Written by Onufry Wojtaszczyk. Prepared by Dustin Tseng and Onufry Wojtaszczyk.
Problem C. Mountain View Written by Onufry Wojtaszczyk. Prepared by Onufry Wojtaszczyk and Andrei Missine.
Problem D. Descending in the Dark Written by David Arthur. Prepared by Onufry Wojtaszczyk and David Arthur.
Contest analysis presented by Onufry Wojtaszczyk, Onufry Wojtaszczyk, Onufry Wojtaszczyk and David Arthur.
Solutions and other problem preparation by Igor Naverniouk, Adam Polak, Andrii Sydorchuk, Pedro Bello, Dave Walker, Bartholomew Furrow, Gary Sivek, Lucas Hosseini, John Dethridge, Petr Mitrichev, Sean Henderson, Tomek Czajka, Witek Jarnicki and Raymond Ho. It's possible Onufry Wojtaszczyk contributed somehow too.
A. Swinging Wild
Problem
You are standing on a ledge in the jungle, and your one true love is standing on a similar ledge at the other side of a swamp infested with snakes, crocodiles and a variety of other unpleasant denizens. Fortunately, there is a number of vines hanging from the canopy of the jungle over the swamp, even more fortunately, you somehow managed to get hold of the first of these vines (see figures below). The canopy of the jungle is at a constant height, and both the ledges are at the same height as the canopy. The vines are simply lines hanging from the canopy at certain points, with differing lengths.
If you happened to be a fictional hero, you would just go swinging wildly and yelling, at some point let go of the vine you hold, fly in the air for some time, catch another vine, swing again, and after a few repetitions you would be holding your one true love in your arms. Unfortunately, you are not a fictional hero, and if you tried that, probably yelling would be the only part you would manage well.
Your plan is a bit more cautious. You will swing on the vine you hold, but instead of letting go, you will catch hold of another vine. Then you will slowly and carefully climb up your original vine, so that the new vine you are holding will become horizontal - either to its full length, or up to the distance between the two vines, whichever is smaller. Then you will rest for a bit, and swing again, to repeat the process. Note that you do not have to catch the first vine you come up against while swinging, you might prefer to swing a bit further and catch some further-off vine instead. You can also climb up the vine you're currently swinging back and forth on to reduce the distance between you and the root of the vine. In effect, this means that you can catch any vine that your vine crosses while swinging. Note that you will not climb down a vine while swinging.
One other thing that sets you apart from any fictional hero is that before you start the whole rather risky procedure you would like to know whether it is actually possible to reach the other side of the jungle this way. And this is the question you have to answer in this problem.
Input
The first line of the input gives the number of test cases, T. T test cases follow. The first line of each test case contains the number N of vines. N lines describing the vines follow, each with a pair of integers di and li - the distance of the vine from your ledge, and the length of the vine, respectively. The last line of the test case contains the distance D to the ledge with your one true love. You start by holding the first vine in hand.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is a YES or a NO. Indicating whether it is possible for you to reach your one true love, given the rules above.
Limits
Memory limit: 1GB.
Time limit: 40 seconds per test set.
0 < di, li, D ≤ 109.
T ≤ 30.
di < di+1.
As you hold the first vine, d0 ≤ l0.
dN-1 < D.
Test set 1 (Visible Verdict)
1 ≤ N ≤ 100.
Test set 2 (Hidden Verdict)
1 ≤ N ≤ 10000.
There will be at most 60000 vines in all the test cases in total.
Sample
4 3 3 4 4 10 6 10 9 3 3 4 4 10 7 10 9 2 6 6 10 3 13 2 6 6 10 3 14
Case #1: YES Case #2: NO Case #3: YES Case #4: NO
In the first case, you hold the first vine 3 units away from where it is attached. You swing wildly, bypass the second vine and just barely catch the third. The picture below depicts the starting situation, and you are able to reach any vine that is rooted anywhere within the red interval:
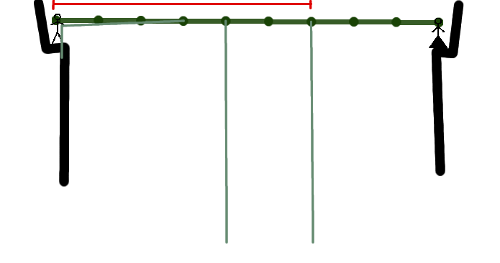
After resting, you climb down the third one and up the first, to find yourself three units from the start, touching the canopy and holding the first and third vines. Now you let go of the first vine, swing again and again just barely reach the ledge, where your one true love awaits. The picture below depicts the situation after you caught the third vine and climbed over to the root of the first one. Again, you could reach any vine rooted within the red interval:
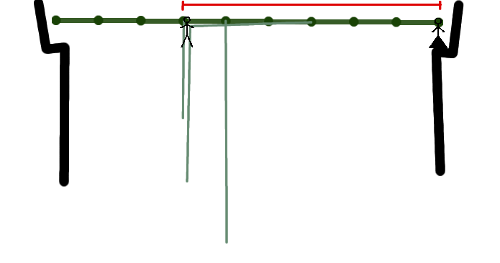
In the second case, you will not reach the third vine in the first swing, so your only choice is to catch the second. However, as it is attached four units from the start, you can (by going up the first vine) give yourself only one unit of swing - clearly too little to reach the third vine. Thus, you can't even reach the third vine, not to mention the other side of the swamp. Better go looking for some way around (or for a new true love).
In the third case, note that if you just swing on the first vine you hold, your path will not intersect the second vine - you have to climb up a bit while swinging (fortunately, you can) to reach the second vine. Remember, you can only climb up while swinging, you cannot climb down (because the vine going up is taut and you can put your weight on it, while the vine going down is swinging freely). In the fourth case, even though you can reach the second vine, it is too short to reach the final ledge.
B. Aerobics
Problem
The aerobics class begins. The trainer says, "Please position yourselves on the training mat so that each one of you has enough space to move your arms around freely, and not hit anybody else." People start milling around on the mat, trying to position themselves properly. Minutes pass, and finally the trainer is so annoyed that he asks you to write a program that will position all the people correctly, hoping it will be quicker than letting them figure it out for themselves!
You are given the dimensions (width and length) of the mat on which the class takes place. For every student, there is a circular area she has to have for herself, with radius equal to the reach of her arms. These circles can not intersect, though they can touch; and the center of each circle (where the student stands) has to be on the mat. Note that the arms can reach outside the mat. You know that there's plenty of space on the mat — the area of the mat is at least five times larger than the total area of the circles required by all the people in the class. It will always be possible for all the people to position themselves as required.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case consists of two lines. The first line contains three integers: N, W and L, denoting the number of students, the width of the mat, and the length of the mat, respectively. The second line contains N integers ri, denoting the reach of the arms of the ith student.
Output
For each test case, output one line containing "Case #n: y", where n is the case number (starting from 1) and y is a string containing 2N numbers, each of which can be an integer or a real number: x1, y1, x2, y2, etc., where the pair (xi, yi) is the position where the ith student should stand (with 0 ≤ xi ≤ W and 0 ≤ yi ≤ L).
As there will likely be multiple ways to position the students on the mat, you may output any correct positioning; but remember that you may not submit an output file more than 200kB in size.
Limits
Memory limit: 1GB.
Time limit: 40 seconds per test set.
1 ≤ T ≤ 50.
1 ≤ W, L ≤ 109.
1 ≤ ri ≤ 105.
The area of the mat is at least 5 times larger than the total area of the circles:
5*π*(r12 + ... + rN2) ≤ W*L.
Test set 1 (Visible Verdict)
1 ≤ N ≤ 10.
Test set 2 (Hidden Verdict)
1 ≤ N ≤ 103.
The total number of circles in all test cases will be ≤ 6000.
Sample
2 2 6 6 1 1 3 320 2 4 3 2
Case #1: 0.0 0.0 6.0 6.0 Case #2: 0.0 0.0 7.0 0.0 12.0 0.0
C. Mountain View
Problem
You are walking through the mountains. It turns out that in this mountain range there is a peak every kilometer, and there are no intermediate peaks. On every peak, you lie down for a rest, look forward, and perceive one of the peaks in front of you to be the highest one. The peak that looks like it's the highest might not really be the highest, for two reasons: there could be a higher peak that is obscured by another peak that's closer to you, and not as high; or you could be looking down, and a faraway peak could look higher than a nearby one.
To be precise, when we say that peak B looks like it's the highest from peak A we mean that B is further down the road than A; all peaks between A and B are below the line connecting the peaks A and B; and all the peaks that are further than B are below or on this line.
You don't know how high each peak is, but you have a very good memory; you've been on all the peaks; and you remember which peak looks like it's the highest from each of them. You would like to invent a set of heights for the peaks that is consistent with that information. Note that you were lying down when looking, so we assume you always looked from the ground level on each peak.
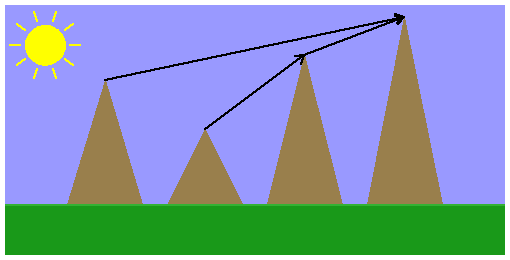
In this example, the fourth peak looks like it's the highest from the first and third peaks. When you're lying on the second peak, you can't see the fourth peak; the third one obscures it, and looks like it's the highest.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case consists of two lines. The first contains one number, N, the number of peaks in the range. You began your trip on peak 1 and went forward to peak N. The next line contains N-1 numbers xi. The i-th number denotes the index of the peak that appeared to be the highest from peak i (note that peak N is the last peak, so there are no other peaks to see from there).
Output
For each test case, output one line containing "Case #n: y1 y2 ... yN", where n is the case number (starting from 1) and yi is the height of the i-th peak. You can output any solution agreeing with the input data, except that all the heights you output have to be integers between 0 and 109, inclusive.
If no solution is possible, output "Case #n: Impossible" instead.
Limits
Memory limit: 1GB.
Time limit: 20 seconds per test set.
1 ≤ T ≤ 30.
i < xi ≤ N.
Test set 1 (Visible Verdict)
2 ≤ N ≤ 10.
Test set 2 (Hidden Verdict)
2 ≤ N ≤ 2000.
Sample
4 6 2 3 4 5 6 4 4 4 4 4 3 4 4 4 4 3 4
Case #1: 10 10 10 10 10 2 Case #2: 10 20 40 80 Case #3: Impossible Case #4: 5 3 6 8
D. Descending in the Dark
Problem
You are on the face of Mount Everest. You need to find shelter before you freeze, and it's dark! What do you do?
The good news is you have already memorized the layout of the mountain. It is a grid with certain squares impassable and other squares containing caves where you can rest for the night. The bad news is you don't know where you are, and it's too steep to climb up. All you can do is move left, right, or down.
Here is an example layout, with '.' representing a passable square, '#' representing an impassable square, and numbers representing caves.
###### ##...# #..#.# #...## #0#..# ####1# ######
Since it is so dark, you will move around by following a plan, which is a series of instructions, each telling you to move one square left, right, or down. If an instruction would take you to a passable square or to a cave, you will follow it. If it would take you to an impassable square, you will have to ignore it. Either way, you will continue on to the next step, and so on, until you have gone through the whole plan.
To help with your descent, you want to find out two things for each cave C:
- What squares is it possible to reach C from? We will label the set of these squares by SC, and the number of them by nC.
- Is there a single plan that, if followed from any square in SC, will finish with you at cave C? If so, we say the cave is lucky.
Note that you might pass by several caves while following a plan. All that matters is what square you finish on after executing all the steps, not what caves you visit along the way.
For example, in the layout above, cave 0 is lucky. There are 9 squares that it can be reached from (including itself), and the plan "left-left-down-down-left-down" will finish with you at the cave from any of those squares.
Input
The first line of the input gives the number of test cases, T. T test cases follow, beginning with a line containing integers R and C, representing the number of rows and columns in the mountain layout.
This is followed by R lines, each containing C characters, describing a mountain layout. As in the example above, a '#' character represents an impassable square, a '.' character represents a passable square, and the digits '0'-'9' represent caves (which are also passable squares).
Output
For each test case, first output one line containing "Case #x:", where x is the case number (starting from 1). For each cave C, starting with 0 and counting up from there, write a line "C: nC LC". Here, C is the cave number, nC is the number of squares you can reach the cave from, and LC is either the string "Lucky" or the string "Unlucky", as defined above.
Limits
Memory limit: 1GB.
Time limit: 40 seconds per test set.
There will be between 1 and 10 caves inclusive.
If there are d caves, they will be labeled with the digits {0, 1, ..., d - 1}, and no two caves will have the same label.
All squares on the boundary of the mountain layout will be impassable.
1 ≤ T ≤ 20.
Test set 1 (Visible Verdict)
3 ≤ R, C ≤ 10.
Test set 2 (Hidden Verdict)
3 ≤ R, C ≤ 60.
Sample
2 7 5 ##### ##0## ##1.# ##2## #3..# #.#.# ##### 7 6 ###### ##...# #..#.# #...## #0#..# ####1# ######
Case #1: 0: 1 Lucky 1: 3 Lucky 2: 4 Unlucky 3: 7 Lucky Case #2: 0: 9 Lucky 1: 11 Unlucky
- For cave 0, you can use the empty plan. If you can reach the cave at all, you are already in the right place!
- For cave 1, you can use the plan right-down-left.
- For cave 3, you can use the plan right-right-left-down-down-down-left.
Analysis — A. Swinging Wild
Translating to a graph problem
To analyse the problem, let us begin with describing the state we can be in at any particular point during traversing the swamp. It is easy to see that we need two items of information to describe this state - which vine are we currently holding on to, and how far away from the root are we holding it.
Once we have such a description, we can frame the problem as a path-finding problem in a graph. We start in the state (0, d0), and we want to any state (i, p) with p + di ≥ D (to simplify, we can also add an artificial N+1st vine where our true love stands and demand that we reach the state (N, p) for any p).
The transitions between states (or, in other words, edges in the graph) are allowed swings we can make. If we currently hold vine i, at p units away from the root, we can swing to any vine j rooted between di - p and di + p, and the new length will be the minimum of |di - dj| and lj. Note that the only use of climbing up a vine is to catch a vine that would be too short to be within our swing path - so we implicitly include it in the transitions described above (and thus do not need extra transitions from (i, p) to (i, p-1)).
Limiting the number of nodes
As described, we could have a large number of states (as there are very many possible vine lengths. A crucial fact to notice is that the second part of the state (the length away from root) is uniquely determined by the previous vine we got here from; and it is independent of where did we hold it (assuming we held it far enough to actually reach this state). This means that there are at most N2 states we will ever consider, as each is determined by a pair of vine indices.
We can now solve the small input. We have a graph with N2 nodes and at most N edges from each node, and we want to verify whether a path between some two nodes exists (we can merge all the target nodes into one node for simplicity). As we have at most N3 edges in total, any standard graph traversal algorithm (like BFS or DFS) will allow us to solve the problem.
Limiting the number of edges
For the large input, a O(N3) solution will be unsatisfactory, and we need a bit more subtlety. There is a number of tricks one can use to beat down the complexity. One is to make use again of the fact that the target node depends only on the vine we start from, and not on the position at which we hold it. This means that there are in fact at most N edges from a given vine - if we manage to reach some vine j from a given vine i when holding it at position A, we do not need to check this edge when considering moves from vine i held at position B (because even if we reach vine j, we will arrive in a state that we have already analysed). Thus, we need to make at most N2 edge traversals to visit all reachable nodes. There are various techniques to actually code this (for instance, for each vine, we could order the other vines by distance from this vine, and each time process this list from the closest vine and remove all traversed edges), we encourage you to explore the options.
An alternative for the large problem
An alternative is to notice another fact - the position part of the state (that is, the distance away from the root that you hold the vine at) never increases. This is because if you swing from vine i to vine j, it means you were holding i at least |di - dj| away from the root, while this quantity is at the same time an upper bound on the position you will hold vine j at.
This means that we can use Dijkstra's algorithm to find, for each vine, the maximum position we can hold this vine at - we treat the decreasing vine position as increasing time, and in each step we analyse what lengths could we obtain for each vine by moving from the current vine, and then choose the vine with the largest length to analyse. This will give us a O(N2logN) solution, which should be fast enough.
Going even faster
A fun fact is that this problem can be solved faster than O(N2), although you didn't need to notice this to solve our data sets. The key fact here is that if you can pass the swamp at all, you can always do it without going backwards (that is, you always catch a vine that's in front of you, you never swing back). An easy way to use this observation is to modify the Dijkstra's algorithm mentioned above to process the vines from first to last, which will turn O(N2logN) into O(N2).
To go down to O(N), we need one more trick. Notice that if we can reach a vine, we will get the largest (meaning best) position if we swing to it from a vine that is as far away as possible. As we move only forward, this means that as soon as we can reach any particular vine, we should note the position achieved and we never need to check any other way of reaching it. This means we can get an O(N) solution by keeping track of the vine we are currently processing and farthest we have reached so far, and from each vine trying to update only vines that we have not reached as yet. As each vine will be updated at most once, and read at most once, we will do O(N) operations.
We encourage you to flesh out the details and try to prove the "never go back" lemma - it's not trivial!
Analysis — B. Aerobics
The key to this problem lies in realizing that there really is a lot of space on the mat to take advantage of, and a number of different approaches will work.
For the small input, putting the circles along one of the longer edge, and - if it runs out - along the opposite edge will work. The precise analysis of why they fit is somewhat tedious, so we will skip it in favor of describing two solutions that can also deal with the large input.
A randomized solution
The large input is a more interesting case. We will describe two solutions that allow one to solve this problem. The first one will be randomized. (If you solved the Equal Sums problem in Round 1B, you should already realize how helpful randomized algorithms can be!).
We will order the circles by decreasing radius. We will then take the circles one by one, and for each circle try to place it on the mat at a random point (that is, put the center of the circle at a random point on the mat). We then check whether it collides with any circle we have placed previously (by directly checking all of them). If it does collide, we try a different random point and repeat until we find one that works. When we succeed in placing all the circles, we're done.
Of course, if we manage to place all the circles, we have found a correct solution. The tricky part is why we will always find a good place to put the new circle in a reasonable time. To see this, let's consider the set of "bad points" - the points where we cannot put the center of a new circle because it would cause a collision. If we are now placing circle j with radius rj, then it will collide with a previously placed circle i if and only if the distance from the new center to the center of circle i is less than ri + rj. This means that the "bad points" are simply a set of circles with radii ri + rj.
What is the total area of the set of bad points? Well, since the set is a group of circles, the area is at most the sum of the areas of the circles. (It can be less because the circles can overlap, but it cannot be more). As we are placing the circles ordered by decreasing radius, we know rj ≤ ri, so the area of the ith "bad" circle is at most π * (2ri)2 = 4π ri2. Here is where we will use that the mat is so large - we see that the total bad area is always at most 80 percent of the mat. Therefore, we have at least a 1 in 5 chance of choosing a good center on every attempt. In particular, it is always possible to find a good center, and it will take us only a few tries.
For each attempt, we have to make O(N) simple checks, and we expect to make at most 5N attempts, so the expected time complexity of this algorithm is O(N2) - easily fast enough.
A deterministic solution
As usual, if we are willing to deal with a bit more complexity in the code, we can get rid of randomness in the solution, taking advantage of all the extra space we have in a different way. One sample way to do this follows.To each circle of radius R we attach a 4R * 2R rectangle as illustrated below:

The top edge of the rectangle passes through the center of the circle. The bottom edge, the left edge, and the right edge are all at a distance of 2R from the center of the circle.
We now place circles one at a time, starting from the ones with the larger radius. We always place each circle in the topmost (and if we have a choice, leftmost) point not covered by any of the rectangles we have already drawn.
An argument similar to the one used in the randomized solution proves that if we place a circle like that, it does not collide with any of the previously placed circles. As we place each point in the topmost available point, the centers of the previously placed circles are necessarily above the last one placed, and so if our new circle would collide with one of the previous ones, it would have to be in the rectangle we associated with it.
Now notice that the areas of all the rectangles we place is the sum of 8R2 = 8 / π times the total area of the circles - which is easily less than the area of the mat. This means we always can place the next circle within the mat.
This solution is somewhat more tricky to code than the previous one (because we have to find the topmost free point, instead of just choosing a random one), but still easier than if we tried to actually stack circles (instead of replacing them by rectangles).
Analysis — C. Mountain View
This problem gives you a lot of freedom in how you approach it, as it is OK to output any sequence of peak heights matching the input data. What follows is one of the possible solutions, but others are possible.
First notice that if from peak 3 we perceive peak 7 as highest, then from peaks 4, 5 and 6 I can surely see no farther than 7, as the peaks have to lie below the line connecting peaks 3 and 7, and no peak after 7 lies above that line (or it would appear higher from peak 3). If this condition is not satisfied, we can safely return "impossible".
So, begin with peak 1, then go to the one appearing to be highest from it, then the apparent highest from it, and so on. Give all these peaks height of 109. Note this sequence necessarily ends on peak N (as it is strictly increasing).
Now sequentially take the first peak A that we haven't assigned a height to yet. As it's the first non-assigned, the previous peak (A-1) has necessarily been assigned, and we can look at the peak that appears highest from A-1. Suppose it's B. We know that when we start a sequence of apparently highest peaks from A, it has to contain at B - it cannot skip B, because the whole sequence has to lie below the [(A-1), B] line), and it is strictly increasing. If the sequence jumps over B, we return "impossible".
Assume the line [(A-1), B] has slope T; our construction will guarantee that T is an integer (notice the slope of the first line is zero). We will want all the peaks on the sequence starting at A to lie on a line passing through peak B and with slope T+1; this determines the line uniquely. If we do it this way, we will not spoil visibilities built before (because the whole line is below the line connecting A-1 and B), and in the sequence for each peak the apparently highest peak will be the next peak in the sequence (as they are all in one line, no peaks with constructed heights lie between A and B, and all the peaks after B are invisible, because they lie below the line connecting (A-1) and B, and thus, even more so, below the line connecting A and B (which has larger slope).
We continue in this fashion. We can check that at any moment of our construction:
- If we assume the peaks that we have not constructed yet do not stand in the way (have, say, a height of zero), then for each peak we already constructed the peak appearing to be the highest is the one we expect to appear highest.
- For any constructed peak A, either A+1 is constructed as well, or no peak between A and the peak visible from A has its height constructed.
- Adding a new sequence upholds these invariants, which proves that when we end, the visibilities are all OK.
Notice that we increase the slope by one for each sequence, so it is at most N at the end, and so the lowest we can get is 109 - N2; thus the heights are all positive.
Analysis — D. Descending in the Dark
The main challenge in this problem is determining whether a cave is lucky. The set of all possible states is huge, so a complete search over all plans is simply not going to work. Fortunately, there is one observation we can use to greatly simplify the task.
Eliminating Backtracking
Fix a cave C, and recall that SC denotes the set of squares from which C can be reached. We will build up our plan one instruction at a time.
Let X be the set of squares that you can be in if you start in SC and follow the plan so far. If X contains a square not in SC, we know the plan cannot work for every starting position. Otherwise, we can be 100% sure that the plan so far is fine! This is because the set of possible squares we are in has either stayed the same or gotten strictly smaller. In particular, if there was a plan that worked from the starting position, we can append it to what we have done so far, and it will still work.
So what does this mean? As long as we don't do a move that adds a square not in SC to the set of possible squares X, we can go ahead and do that move, and it will still be possible to finish. In particular, we can always move left and right whenever we want, since moving left or right can never move you out of SC.
All You Need Is Down!
Even with the previous observation, we still have work to do. We now know all the moves that can be done safely, but the state space is still huge. We can't find just any move; we need one that makes progress.
Here is where it is important that you cannot go up the mountain. Suppose you can add a Down move to the plan, satisfying the following two properties:
- There is at least one position in X from which you can actually move down. (Without this, the Down move will never do anything, and so is useless!)
- There is no position in X from which a down move will take you outside of XC.
Since the sum of the heights is a positive integer, you will eventually have to stop making Down moves. At that point, you are stuck in one or more horizontal intervals. If there is just one interval and it contains the cave, the plan can be finished successfully. Otherwise, you're screwed! And remember, since this set of squares is a subset of what you started with, you were in fact screwed from the start.
Can You Go Down?
Only one question remains: given a set of positions X reachable from the start, can you come up with a valid plan that includes at least one Down move?
X must be contained in a set of horizontal intervals, bounded by impassable squares to the left and right. Since it is always safe to move left and right, we can keep moving left until X is actually just the leftmost square in each of these intervals. If we cannot make progress from that situation, we have already shown we are lost.
As we perform left and right moves from there, our position within each interval might change. However, note that if two intervals have the same length, our relative horizontal positions within them will always be the same. Therefore, let's define xj to be our relative horizontal position within all intervals of length j. (In particular, xj = 0 if we are in the leftmost position, and xj = j - 1 if we are in the rightmost position.)
Lemma: It is possible to reach position (x1, x2, ...) using left and right moves if and only if xi ≤ xj ≤ xi + j - i for all i < j.
Proof: First we show xi ≤ xj. This is true initially. If it ever failed after some sequence of moves, it would be because xi and xj were equal, and then either:
- We moved left, and only xj was able to move.
- We moved right, and only xi was able to move.
Conversely, any set of positions with xi ≤ xj ≤ xi + j - i really can be reached via the following algorithm:
- Start with each xi = 0.
- Loop from i = largest interval length down to 2.
- Move i-2 + xi - xi-1 times to the right, and then i-2 times to the left.
We are now essentially done. We need to determine if there is set of positions {xi} that can be reached for which it is safe to move down. Once you have gotten this far, you can finish it off with dynamic programming. Here is some pseudo-code that determines whether there is a set of positions from which it is possible to move down and make progress:
old_safety = [SAFE] * (n+1)
for length in {n, n-1, ..., 1}:
for i in [0, length-1]:
pos_safety[i] = best(old_safety[i], old_safety[i+1])
if moving down leaves SC:
pos_safety[i] = UNSAFE
elif moving down is legal and pos_safety[i] == SAFE:
pos_safety[i] = SAFE_WITH_PROGRESS
old_safety = pos_safety
return (pos_safety[0] == SAFE_WITH_PROGRESS)
This is a good starting point, but you would still have to tweak it to actually record what the right xi is for all i.
Putting it all together, we repeatedly use the above algorithm to see if it is possible to make a down move. If so, we do it and repeat. Otherwise, we stop. If the only remaining interval is the one containing the cave, then that cave is lucky. Otherwise, it is not!
Since there are no correct submissions for the large input during the contest, we provide here a full java solution (by Petr Mitrichev) so everyone can use it to generate correct outputs for various inputs.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class Dark {
static class Segment {
int len;
long goodExitMask;
long badExitMask;
}
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
int numTests = Integer.parseInt(reader.readLine());
for (int testId = 0; testId < numTests; ++testId) {
String[] parts = reader.readLine().split(" ", -1);
if (parts.length != 2) throw new RuntimeException();
int rows = Integer.parseInt(parts[0]);
int cols = Integer.parseInt(parts[1]);
String[] field = new String[rows];
for (int r = 0; r < rows; ++r) {
field[r] = reader.readLine();
if (field[r].length() != cols) throw new RuntimeException();
}
System.out.println("Case #" + (testId + 1) + ":");
for (char caveId = '0'; caveId <= '9'; ++caveId) {
int cr = -1;
int cc = -1;
for (int r = 0; r < rows; ++r)
for (int c = 0; c < cols; ++c)
if (field[r].charAt(c) == caveId) {
cr = r;
cc = c;
}
if (cr < 0) continue;
boolean[][] reach = new boolean[rows][cols];
reach[cr][cc] = true;
int nc = 1;
while (true) {
boolean updated = false;
for (int r = 0; r < rows; ++r)
for (int c = 0; c < cols; ++c)
if (reach[r][c]) {
if (r > 0 && field[r - 1].charAt(c) != '#' && !reach[r - 1][c]) {
reach[r - 1][c] = true;
++nc;
updated = true;
}
if (c > 0 && field[r].charAt(c - 1) != '#' && !reach[r][c - 1]) {
reach[r][c - 1] = true;
++nc;
updated = true;
}
if (c + 1 < cols && field[r].charAt(c + 1) != '#' && !reach[r][c + 1]) {
reach[r][c + 1] = true;
++nc;
updated = true;
}
}
if (!updated) break;
}
List<Segment> segments = new ArrayList<Segment>();
for (int r = 0; r <= cr; ++r)
for (int c = 0; c < cols; ++c)
if (reach[r][c] && (c == 0 || !reach[r][c - 1])) {
int c1 = c;
while (reach[r][c1 + 1]) ++c1;
Segment s = new Segment();
s.len = c1 - c + 1;
for (int pos = c; pos <= c1; ++pos) {
if (r + 1 < rows && field[r + 1].charAt(pos) != '#') {
if (reach[r + 1][pos])
s.goodExitMask |= 1L << (pos - c);
else
s.badExitMask |= 1L << (pos - c);
}
}
segments.add(s);
}
while (true) {
int maxLen = 0;
for (Segment s : segments)
maxLen = Math.max(maxLen, s.len);
long[] badByLen = new long[maxLen + 1];
for (Segment s : segments) {
badByLen[s.len] |= s.badExitMask;
}
long[] possible = new long[maxLen + 1];
possible[1] = 1;
for (int len = 1; len <= maxLen; ++len) {
possible[len] &= ~badByLen[len];
if (len < maxLen) {
possible[len + 1] = possible[len] | (possible[len] << 1);
}
}
for (int len = maxLen; len > 1; --len) {
possible[len - 1] &= possible[len] | (possible[len] >> 1);
}
List<Segment> remaining = new ArrayList<Segment>();
for (Segment s : segments)
if ((s.goodExitMask & possible[s.len]) == 0) {
remaining.add(s);
}
if (remaining.size() == segments.size()) break;
segments = remaining;
}
System.out.println(caveId + ": " + nc + " " + (segments.size() == 1 ? "Lucky" : "Unlucky"));
}
}
}
}