Google Code Jam Archive — Round 1C 2012 problems
Overview
Round 1C was the last chance to get to round 2, with the top 1000 advancing.
Problem A was an easy graph theory problem, and it was first finished in under 8 minutes! Any algorithm for counting paths between nodes sufficed to solve the problem.
Problem C was a dynamic programming problem, similar to the standard Longest Common Subsequence problem. The input strings each consisted of a small number of runs of equal letters, but each run could be very large. Since the strings can be so large, standard algorithms for solving the LCS problem had to be modified to take advantage of the special form of the input, making this problem much more challenging.
Problem B was a subtle physics problem that turned out to be the hardest in the set. It appears to require dynamic programming with a state that includes the position, velocity, and time of the car. But some careful reasoning shows that there's always an optimal strategy that consists of only two phases -- staying still for a period of time, then using the maximum acceleration, with no braking, until reaching the destination. This simplifies the mathematics considerably, as we only need to figure out how long to wait.
mystic won the round by a comfortable margin, finishing the whole set in under an hour. Congratulations to the 1000 advancers!
Cast
Problem A. Diamond Inheritance Written and prepared by Khaled Hafez.
Problem B. Out of Gas Written by Bartholomew Furrow. Prepared by Bartholomew Furrow and Yiu Yu Ho.
Problem C. Box Factory Written by David Arthur. Prepared by David Arthur and Luka Kalinovcic.
Contest analysis presented by John Dethridge, Onufry Wojtaszczyk, and John Dethridge again.
Solutions and other problem preparation by Igor Naverniouk, Adam Polak, Luka Kalinovcic, John Dethridge, Alexander Georgiev, Sean Henderson, Ahmed Aly, Muntasir Khan and Nikolay Kurtov.
A. Diamond Inheritance
Problem
You are asked to help diagnose class diagrams to identify instances of diamond inheritance. The following example class diagram illustrates the property of diamond inheritance. There are four classes: A, B, C and D. An arrow pointing from X to Y indicates that class X inherits from class Y.
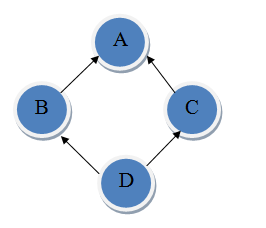
In this class diagram, D inherits from both B and C, B inherits from A, and C also inherits from A. An inheritance path from X to Y is defined as a sequence of classes X, C1, C2, C3, ..., Cn, Y where X inherits from C1, Ci inherits from Ci + 1 for 1 ≤ i ≤ n - 1, and Cn inherits from Y. There are two inheritance paths from D to A in the example above. The first path is D, B, A and the second path is D, C, A.
A class diagram is said to contain a diamond inheritance if there exists a pair of classes X and Y such that there are at least two different inheritance paths from X to Y. The above class diagram is a classic example of diamond inheritance. Your task is to determine whether or not a given class diagram contains a diamond inheritance.
Input
The first line of the input gives the number of test cases, T. T test cases follow, each specifies a class diagram. The first line of each test case gives the number of classes in this diagram, N. The classes are numbered from 1 to N. N lines follow. The ith line starts with a non-negative integer Mi indicating the number of classes that class i inherits from. This is followed by Mi distinct positive integers each from 1 to N representing those classes. You may assume that:
- If there is an inheritance path from X to Y then there is no inheritance path from Y to X.
- A class will never inherit from itself.
Output
For each diagram, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is "Yes" if the class diagram contains a diamond inheritance, "No" otherwise.
Limits
Memory limit: 1GB.
Time limit: 40 seconds per test set.
1 ≤ T ≤ 50.
0 ≤ Mi ≤ 10.
Test set 1 (Visible Verdict)
1 ≤ N ≤ 50.
Test set 2 (Hidden Verdict)
1 ≤ N ≤ 1,000.
Sample
3 3 1 2 1 3 0 5 2 2 3 1 4 1 5 1 5 0 3 2 2 3 1 3 0
Case #1: No Case #2: Yes Case #3: Yes
B. Out of Gas
Problem
Your car is out of gas, and you want to get home as quickly as possible! Fortunately, your home is at the bottom of a hill and you (in your car) are at the top of it. Unfortunately, there is a car in front of you, and you can't move past it. Fortunately, your brakes are working and they are very powerful.
You start at the top of the hill with speed 0 m/s at time 0 seconds. Gravity is pulling your car down the hill with a constant acceleration. At any time, you can use your brakes to reduce your speed, or temporarily reduce your acceleration, by any amount.
How quickly can you reach your home if you use your brakes in the best possible way?
Input
The first line of the input gives the number of test cases, T. T test cases follow. The first line of each test case contains three space-separated numbers: a real-valued number D, the distance in meters to your home down the hill; and two integers, N and A. The distance D will be given in exactly 6 decimal places.
N lines follow, each of which contains two space-separated, real-valued numbers: a time ti in seconds, and a position xi in meters. The ti and xi values will be given in exactly 6 decimal places.
One line follows, with A space-separated, real-valued numbers ai, which are accelerations in m/s2. The accelerations will be given in exactly 2 decimal places.
The other car's position is specified by the (ti, xi) pairs. The car's position at time ti seconds is xi meters measured from the top of the hill (i.e. your initial position). The car travels at constant speed between time ti and ti+1. The positions and times will both be given in increasing order, with t0=0.
For example, if t5=10, x5=20, t6=20, x6=40, then 10 seconds after the start, the other car is 20 meters down the hill; 15 seconds after the start, the other car is 30 meters down the hill; and 20 seconds after the start, the other car is 40 meters down the hill.
Output
For each test case, output one line containing "Case #c:", where c is the case number (starting from 1). Then output A lines, the ith of which contains the minimum number of seconds it takes you to reach your home if your acceleration down the hill due to gravity is ai, and you use your brakes in the best possible way. Answers within an absolute or relative error of 10-6 of the correct answer will be accepted. There should be no blank lines in the output.
Notes
Position and Acceleration: An object with a constant acceleration a m/s2 and starting speed of v0 m/s will move a distance of v0*t + 0.5*a*t2 after t seconds.
2 m/s2 with an initial speed of 0 m/s, and the other car is stopped at x=1, it will take exactly 1 second to reach the other car.
The other car: You may never pass the other car, which means that at no time shall your distance down the hill be greater than that of the other car. It may be equal. The cars should be considered as point masses.
Output values: You can print as many decimal places as you like in the output. We will read and compare your answers with ours, and at that time we will be using 10-6 as a threshold for inaccuracy. So 25, 25.0 and 25.000000 are the same from our perspective. Trailing zeros after the decimal point does not matter.
Limits
Memory limit: 1GB.
1 ≤ T ≤ 20.
1.0 ≤ D ≤ 104.
1.0 ≤ ai ≤ 9.81.
0.0 ≤ ti ≤ 105.
0.0 ≤ xi ≤ 105.
ti < ti+1.
xi < xi+1.
t0 = 0
xN-1 ≥ D.
Test set 1 (Visible Verdict)
Time limit: 60 seconds.
1 ≤ N ≤ 2.
1 ≤ A ≤ 10.
Test set 2 (Hidden Verdict)
Time limit: 120 seconds.
1 ≤ N ≤ 2000.
1 ≤ A ≤ 250.
Sample
3 1000.000000 2 3 0.000000 20.500000 25.000000 1000.000000 1.00 5.00 9.81 50.000000 2 2 0.000000 0.000000 100000.000000 100.000000 1.00 1.01 10000.000000 3 1 0.000000 0.000000 10000.000000 0.100000 10000.100000 100000.000000 1.00
Case #1: 44.7213595 25.000000 25.0 Case #2: 50000.0 50000.0 Case #3: 10140.974143
C. Box Factory
Problem
You own a factory with two assembly lines. The first assembly line makes boxes, and the second assembly line makes toys to put in those boxes. Each type of box goes with one type of toy and vice-versa.
At the beginning, you pick up a box from the first assembly line and a toy from the second assembly line. You then have a few options.
- You can always throw out the box and pick up the next one.
- You can always throw out the toy and pick up the next one.
- If the box and toy are the same type, you can put the toy in the box, and send it out to customers.
Warning: The two assembly lines make a lot of boxes and toys. However, they tend to make one kind of thing for a long period of time before switching.
Input
The first line of the input gives the number of test cases, T. T test cases follow.
Each test case begins with a line contains two integers N and M. It is followed by a line containing 2 * N integers a1, A1, a2, A2, ..., aN, AN, and another line containing 2 * M integers b1, B1, b2, B2, ..., bM, BM.
This means that the first assembly line will make a1 boxes of type A1, then a2 boxes of type A2, etc., until it finishes with aN boxes of type AN. Similarly, the second assembly will make b1 toys of type B1, followed by b2 toys of type B2, etc., until it finishes with bM toys of type BM.
A toy can be matched with a box if and only if they have the same type number.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1), and y is the largest number of boxed toys that you can send out to customers.
Limits
Memory limit: 1GB.
Time limit: 30 seconds per test set.
1 ≤ T ≤ 100.
1 ≤ ai, bi ≤ 1016.
1 ≤ Ai, Bi ≤ 100.
Test set 1 (Visible Verdict)
1 ≤ N ≤ 3.
1 ≤ M ≤ 100.
Test set 2 (Hidden Verdict)
1 ≤ N, M ≤ 100.
Sample
4 3 3 10 1 20 2 25 3 10 2 30 3 20 1 3 5 10 1 6 2 10 1 5 1 3 2 10 1 3 2 5 1 3 5 10 1 6 2 10 1 5 1 6 2 10 1 6 2 5 1 1 1 5000000 10 5000000 100
Case #1: 35 Case #2: 20 Case #3: 21 Case #4: 0
Analysis — A. Diamond Inheritance
We are given a directed graph, and have to determine if there is a pair of nodes (X,Y) such that there are two or more paths from X to Y.
For each node, we do a depth-first search with that node as the root. If during the depth-first search we reach the same node twice, then we must have followed two different paths to get to that node from the root node, so we have found a pair (X,Y). Conversely, if there are two paths between X and Y, we will reach Y at least twice when doing a DFS from X. So if this algorithm finds no pair (X,Y), then none exists in the graph.
If there are V nodes and E edges in a graph, then a DFS is O(V+E) in general. But each DFS will never follow more than V edges, because after following that many edges, some node will have been reached twice, so we can stop at that point. Therefore this algorithm is O(V2).
We can also just use a variation of Floyd's algorithm, which is O(V3), but very simple to write. With only 1000 nodes in the graph, a fast implementation will finish within the time limit.
Analysis — B. Out of Gas
This was a hard problem to wrap your head around, as evidenced by the results. The final solution was, however, surprisingly simple (although the argumentation for it is not).
Let us first consider a single case, with a single acceleration value a, and an arbitrarily large N. Suppose some strategy S1 takes you home in time T. Obviously a*T2 / 2 ≥ D, as a*T2 / 2 is the distance we travel if we start accelerating immediately and never brake.
We can propose an alternate strategy S2: first stop and wait for time T - sqrt(2 D/ A), and then start accelerating full speed and never brake. This will also bring you home in time T.
We have to prove that if S1 did not collide with the other car, neither will S2. We prove this by checking that S2 arrives at any point between the top of the hill and your home no earlier than S1.
Assume S1 was at some point X later than S2. Notice that the speed of S1 coming into X had to be larger than the speed of S2 — otherwise even accelerating full speed will not let S1 catch up with S2. But it is impossible to achieve a faster speed at X than S2: strategy S2 accelerated all the way from the top of the hill to X.
So, now we only need to consider strategies such as S1. We now just need to determine how long do we need to wait on the top of the hill.
One last thing to notice is that if the other car moves at constant speed between xi and xi+1, and our strategy does not put us in front of the other car at xi or at xi+1, then it does not intercept the other car in any intermediate point either. We know that because if we did intercept it in some intermediate point, it would mean that we were moving faster than the other car at the time of interception; and since we're accelerating, and the other car's speed is constant, we would end up in front of it at xi+1. Therefore passing the other car between xi and xi+1 leads to a contradiction, and it must be the case that we don't pass it.
With this reasoning complete, we now have two possible algorithms. One is a binary search: To check if a given waiting time T is long enough, we just need to check all the N points at which the other car can change its speed. To achieve a precision of 10-6, we will need around 40 iterations in the binary search. This means we solve each test case in O(N A) time, with the constant 40 hidden in the big-O notation — fast enough.
If we are worried about the constant factor of 40, we can also iterate over all points xi, and for each calculate the minimum waiting time needed not to intercept the other car at this point: ti - sqrt(2xi/a) for all i such that xi < D (you also have to include the moment where the other car reaches your house). This will make our solution run in O(N A) time without the pesky constant.
Analysis — C. Box Factory
This problem is a variation of the Longest Common Subsequence problem, which is to find the longest string of characters which occurs as a subsequence of each of two strings (a string S is a subsequence of a string T if S occurs in T, possibly with more characters inserted between the elements of S.) In this case, the first "string" is the sequence of types of each box produced by the factory, and the second "string" is the sequence of types of each toy produced by the factory.
A dynamic programming algorithm for this problem is to find the maximum number of toys that could be placed in boxes using the first x boxes and the first y toys. Let this value be f[x][y]. Then f[x][y] is equal to the maximum of:
- f[x-1][y]
- f[x][y-1]
- f[x-1][y-1]+1
Unfortunately, even though the number of runs of boxes and toys is small, the total number of boxes and toys can be very large, so this algorithm is not practical. But we can modify it so that f[x][y] will be the maximum number of toys that could be placed in boxes using the first x runs of boxes and the first y runs of toys. Now f[x][y] is the maximum of:
- f[x-1][y]
- f[x][y-1]
- f[a][b]+g(a,b,x,y), for all a<x, b<y
This algorithm is O(n4). Another improvement can reduce this again to O(n3), which we leave as an exercise to the reader!