Google Code Jam Archive — Qualification Round 2012 problems
Overview
Google Code Jam 2012 has begun, and our contestants have made a huge showing! We have 15692 qualifiers, out of 20613 people who downloaded at least one input. We had contestants representing 149 different regions of the world, using 73 programming languages. All those numbers are records for us!
This year marked a change to our rules: before, every problem had to have one Small input and one Large input. This year we led off with a problem that had only a Small input, and we might make other problems that are unusual in that way as the contest goes on.
Cast
Problem A. Speaking in Tongues Written and prepared by David Arthur.
Problem B. Dancing With the Googlers Written by Bartholomew Furrow. Prepared by Onufry Wojtaszczyk and Bartholomew Furrow.
Problem C. Recycled Numbers Written by David Arthur. Prepared by David Arthur and Sean Henderson.
Problem D. Hall of Mirrors Written by David Arthur. Prepared by Bartholomew Furrow.
Contest analysis presented by David Arthur, Tomek Czajka, Ahmed Aly, and David Arthur again.
Solutions and other problem preparation by Igor Naverniouk, Adam Polak, Andrei Missine, John Dethridge, Jon Calhoun, Luka Kalinovcic, Khaled Hafez, and Tim Kirchner.
A. Speaking in Tongues
Problem
We have come up with the best possible language here at Google, called Googlerese. To translate text into Googlerese, we take any message and replace each English letter with another English letter. This mapping is one-to-one and onto, which means that the same input letter always gets replaced with the same output letter, and different input letters always get replaced with different output letters. A letter may be replaced by itself. Spaces are left as-is.
For example (and here is a hint!), our awesome translation algorithm includes the following three mappings: 'a' -> 'y', 'o' -> 'e', and 'z' -> 'q'. This means that "a zoo" will become "y qee".
Googlerese is based on the best possible replacement mapping, and we will never change it. It will always be the same. In every test case. We will not tell you the rest of our mapping because that would make the problem too easy, but there are a few examples below that may help.
Given some text in Googlerese, can you translate it to back to normal text?
Solving this problem
Usually, Google Code Jam problems have 1 Small input and 1 Large input. This problem has only 1 Small input. Once you have solved the Small input, you have finished solving this problem.
Input
The first line of the input gives the number of test cases, T. T test cases follow, one per line.
Each line consists of a string G in Googlerese, made up of one or more words containing the letters 'a' - 'z'. There will be exactly one space (' ') character between consecutive words and no spaces at the beginning or at the end of any line.
Output
For each test case, output one line containing "Case #X: S" where X is the case number and S is the string that becomes G in Googlerese.
Limits
Time limit: 20 seconds.
Memory limit: 1GB.
There is only one test set which has visible verdict.
1 ≤ T ≤ 30.
G contains at most 100 characters.
None of the text is guaranteed to be valid English.
Sample
3 ejp mysljylc kd kxveddknmc re jsicpdrysi rbcpc ypc rtcsra dkh wyfrepkym veddknkmkrkcd de kr kd eoya kw aej tysr re ujdr lkgc jv
Case #1: our language is impossible to understand Case #2: there are twenty six factorial possibilities Case #3: so it is okay if you want to just give up
B. Dancing With the Googlers
Problem
You're watching a show where Googlers (employees of Google) dance, and then each dancer is given a triplet of scores by three judges. Each triplet of scores consists of three integer scores from 0 to 10 inclusive. The judges have very similar standards, so it's surprising if a triplet of scores contains two scores that are 2 apart. No triplet of scores contains scores that are more than 2 apart.
For example: (8, 8, 8) and (7, 8, 7) are not surprising. (6, 7, 8) and (6, 8, 8) are surprising. (7, 6, 9) will never happen.
The total points for a Googler is the sum of the three scores in that Googler's triplet of scores. The best result for a Googler is the maximum of the three scores in that Googler's triplet of scores. Given the total points for each Googler, as well as the number of surprising triplets of scores, what is the maximum number of Googlers that could have had a best result of at least p?
For example, suppose there were 6 Googlers, and they had the following total points:
29, 20, 8, 18, 18, 21. You remember that there were 2 surprising triplets of scores, and you want to know how many Googlers could have gotten a best result of 8 or better.
With those total points, and knowing that two of the triplets were surprising, the triplets of scores could have been:
10 9 10 6 6 8 (*) 2 3 3 6 6 6 6 6 6 6 7 8 (*)The cases marked with a (*) are the surprising cases. This gives us 3 Googlers who got at least one score of 8 or better. There's no series of triplets of scores that would give us a higher number than 3, so the answer is 3.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case consists of a single line containing integers separated by single spaces. The first integer will be N, the number of Googlers, and the second integer will be S, the number of surprising triplets of scores. The third integer will be p, as described above. Next will be N integers ti: the total points of the Googlers.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is the maximum number of Googlers who could have had a best result of greater than or equal to p.
Limits
Time limit: 40 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 100.
0 ≤ S ≤ N.
0 ≤ p ≤ 10.
0 ≤ ti ≤ 30.
At least S of the ti values will be between 2 and 28, inclusive.
Test set 1 (Visible Verdict)
1 ≤ N ≤ 3.
Test set 2 (Hidden Verdict)
1 ≤ N ≤ 100.
Sample
4 3 1 5 15 13 11 3 0 8 23 22 21 2 1 1 8 0 6 2 8 29 20 8 18 18 21
Case #1: 3 Case #2: 2 Case #3: 1 Case #4: 3
C. Recycled Numbers
Problem
Do you ever become frustrated with television because you keep seeing the same things, recycled over and over again? Well I personally don't care about television, but I do sometimes feel that way about numbers.
Let's say a pair of distinct positive integers (n, m) is recycled if you can obtain m by moving some digits from the back of n to the front without changing their order. For example, (12345, 34512) is a recycled pair since you can obtain 34512 by moving 345 from the end of 12345 to the front. Note that n and m must have the same number of digits in order to be a recycled pair. Neither n nor m can have leading zeros.
Given integers A and B with the same number of digits and no leading zeros, how many distinct recycled pairs (n, m) are there with A ≤ n < m ≤ B?
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case consists of a single line containing the integers A and B.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1), and y is the number of recycled pairs (n, m) with A ≤ n < m ≤ B.
Limits
Memory limit: 1GB.
Time limit: 30 seconds per test set.
1 ≤ T ≤ 50.
A and B have the same number of digits.
Test set 1 (Visible Verdict)
1 ≤ A ≤ B ≤ 1000.
Test set 2 (Hidden Verdict)
1 ≤ A ≤ B ≤ 2000000.
Sample
4 1 9 10 40 100 500 1111 2222
Case #1: 0 Case #2: 3 Case #3: 156 Case #4: 287
Are we sure about the output to Case #4?
Yes, we're sure about the output to Case #4.
D. Hall of Mirrors
Problem
You live in a 2-dimensional plane, and one of your favourite places to visit is the Hall of Mirrors. The Hall of Mirrors is a room (a 2-dimensional room, of course) that is laid out in a grid. Every square on the grid contains either a square mirror, empty space, or you. You have width 0 and height 0, and you are located in the exact centre of your grid square.
Despite being very small, you can see your reflection when it is reflected back to you exactly. For example, consider the following layout, where '#' indicates a square mirror that completely fills its square, '.' indicates empty space, and the capital letter 'X' indicates you are in the center of that square:
###### #..X.# #.#..# #...## ######If you look straight up or straight to the right, you will be able to see your reflection.
Unfortunately in the Hall of Mirrors it is very foggy, so you can't see further than D units away. Suppose D=3. If you look up, your reflection will be 1 unit away (0.5 to the mirror, and 0.5 back). If you look right, your reflection will be 3 units away (1.5 to the mirror, and 1.5 back), and you will be able to see it. If you look down, your reflection will be 5 units away and you won't be able to see it.
It's important to understand how light travels in the Hall of Mirrors. Light travels in a straight line until it hits a mirror. If light hits any part of a mirror but its corner, it will be reflected in the normal way: it will bounce off with an angle of reflection equal to the angle of incidence. If, on the other hand, the light would touch the corner of a mirror, the situation is more complicated. The following diagrams explain the cases:
In the following cases, light approaches a corner and is reflected, changing its direction:
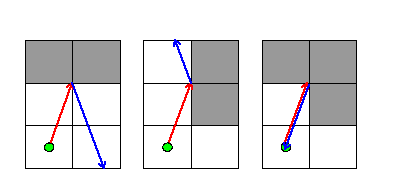
In the first two cases, light approached two adjacent mirrors at the point where they met. Light was reflected in the same way as if it had hit the middle of a long mirror. In the third case, light approached the corners of three adjacent mirrors, and returned in exactly the direction it came from.
In the following cases, light approaches the corners of one or more mirrors, but does not bounce, and instead continues in the same direction:
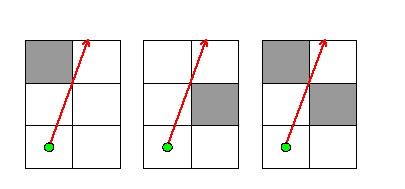
This happens when light reaches distance 0 from the corner of a mirror, but would not have to pass through the mirror in order to continue in the same direction. In this way, a ray of light can pass between two mirrors that are diagonally adjacent to each other -- effectively going through a space of size 0. Good thing it's of size 0 too, so it fits!
In the final case, light approaches the corner of one mirror and is destroyed:
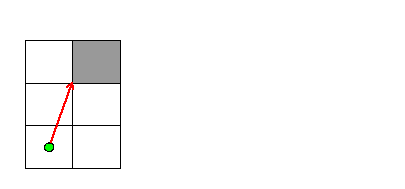
The mirror was in the path of the light, and the ray of light didn't approach the corners of any other mirrors.
Note that light stops when it hits you, but it has to hit the exact centre of your grid square.
How many images of yourself can you see?
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case starts with a line containing three space-separated integers, H, W and D. H lines follow, and each contains W characters. The characters constitute a map of the Hall of Mirrors for that test case, as described above.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is the number of reflections of yourself you can see.
Limits
Memory limit: 1GB.
Time limit: 60 seconds per test set.
1 ≤ T ≤ 100.
3 ≤ H, W ≤ 30.
1 ≤ D ≤ 50.
All characters in each map will be '#', '.', or 'X'.
Exactly one character in each map will be 'X'.
The first row, the last row, the first column and the last column of each map will be entirely filled with '#' characters.
Test set 1 (Visible Verdict)
There will be no more than 2W+2H-4 '#' characters.
Test set 2 (Hidden Verdict)
The restriction from the Small dataset does not apply.
Sample
6 3 3 1 ### #X# ### 3 3 2 ### #X# ### 4 3 8 ### #X# #.# ### 7 7 4 ####### #.....# #.....# #..X..# #....## #.....# ####### 5 6 3 ###### #..X.# #.#..# #...## ###### 5 6 10 ###### #..X.# #.#..# #...## ######
Case #1: 4 Case #2: 8 Case #3: 68 Case #4: 0 Case #5: 2 Case #6: 28
In the first case, light travels exactly distance 1 if you look directly up, down, left or right.
In the second case, light travels distance 1.414... if you look up-right, up-left, down-right or down-left. Since light does not travel through you, looking directly up only shows you one image of yourself.
In the fifth case, while the nearby mirror is close enough to reflect light back to you, light that hits the corner of the mirror is destroyed rather than reflected.
Analysis — A. Speaking in Tongues
In most Google Code Jam problems, each test case is completely separate and nothing you learn from one will be useful in another. This problem was different however:
"Googlerese is based on the best possible replacement mapping, and we will never change it. It will always be the same. In every test case."
We meant it when we said this! There really is just one mapping, and the main challenge here is figuring out what it is. Fortunately, there is a lot we can learn from the sample input and output. For example, by looking at the first word in the first line, we know that "our" becomes "ejp" in Googlerese, so 'o' -> 'e', 'u' -> 'j', and 'r' -> 'p'. If you go through the entire text, you will that there is almost enough information to reconstruct the entire mapping:
'a' -> 'y' 'b' -> 'n' 'c' -> 'f' 'd' -> 'i' 'e' -> 'c' 'f' -> 'w' 'g' -> 'l' 'h' -> 'b' 'i' -> 'k' 'j' -> 'u' 'k' -> 'o' 'l' -> 'm' 'm' -> 'x' 'n' -> 's' 'o' -> 'e' 'p' -> 'v' 'q' -> ??? 'r' -> 'p' 's' -> 'd' 't' -> 'r' 'u' -> 'j' 'v' -> 'g' 'w' -> 't' 'x' -> 'h' 'y' -> 'a' 'z' -> ???
We just need to figure out how to translate 'q' and 'z'. But if you read the problem statement carefully, you will notice there was one more example we gave you! "a zoo" gets translated to "y qee". This means that 'z' gets mapped to 'q'.
Next we have to figure out what 'q' gets mapped to. For this part, you need to remember that every letter gets mapped to something different. And if you look carefully, there is already a letter getting mapped to everything except for 'z'. This leaves only one possibity: 'q' must get mapped to 'z'.
And now we have the full translation mapping, and all we need to do is write a program to apply it to a bunch of text. Here is a solution in Python:
translate_to_english = {
' ': ' ', 'a': 'y', 'b': 'h', 'c': 'e', 'd': 's',
'e': 'o', 'f': 'c', 'g': 'v', 'h': 'x', 'i': 'd',
'j': 'u', 'k': 'i', 'l': 'g', 'm': 'l', 'n': 'b',
'o': 'k', 'p': 'r', 'q': 'z', 'r': 't', 's': 'n',
't': 'w', 'u': 'j', 'v': 'p', 'w': 'f', 'x': 'm',
'y': 'a', 'z': 'q'}
for tc in xrange(1, int(raw_input()) + 1):
english = ''.join(
[translate_to_english[ch] for ch in raw_input()])
print 'Case #%d: %s' % (tc, english)
Analysis — B. Dancing With the Googlers
Clever contestants will have noticed that this problem might be based on an actual television show. The author of the problem found himself watching an episode of Dancing With the Stars (the show and its distributor, BBC Worldwide, do not endorse and are not involved with Google Code Jam), and having forgotten whether any of the contestants had earned a score of at least 8 from any of the judges.
The judges on that show very often agree within 1 point of each other, and it really is surprising when they disagree by so much. There are a few key observations that help us solve this problem:
- Any non-surprising score is expressed uniquely by an unordered triplet of judges' scores. 21 must be 7 7 7; 22 must be 7 7 8; 23 must be 7 8 8.
- There only a few kinds of surprising scores. 21 could be 6 7 8; 22 could be 6 8 8; 23 could be 9 7 7. There's a repeating pattern of surprising scores that extends from 2 (0, 0, 2) to 28 (8, 10, 10).
- The repeating pattern stops at 2 and 28 because 1 and 29 can't be surprising: we can't use (-1, 1, 1) for 1: -1 is not allowed as a score. We also can't use (9, 9, 11) for 29.
Putting all of these facts together, we can easily construct a mapping from each total score to its best result if it's surprising, and to its best result if it isn't surprising:
unsurprising(0) = 0 unsurprising(1) = 1 unsurprising(2) = 1 unsurprising(n) = unsuprising(n-3) + 1 unsurprising(n) = ceiling(n/3), for 0 <= n <= 30 surprising(2) = 2 surprising(3) = 2 surprising(4) = 2 surprising(5) = 3 surprising(n) = surprising(n-3) + 1 surprising(n) = ceiling((n-1)/3) + 1, for 2 <= n <= 28
Many contestants wrote an initial solution that didn't take into account that 0, 1, 29 and 30 can't be surprising, and so failed one of our sample inputs. That's what they're there for!
One way to build the tables of unsurprising(n) and surprising(n) that doesn't require so much thought could involve writing three loops to go through all possible sets of judges' scores, checking whether each combination of three was valid or surprising, and building the maps that way.
Now, for each value ti we have one of three cases:
- unsurprising(ti) >= p. This Googler can be "good" (i.e. have a maximum score of at least p) even with an unsurprising triplet.
- 2 <= ti <= 28 and surprising(ti) >= p > unsurprising(ti). This Googler can be "good" only by using a surprising triplet.
- Otherwise, the Googler can't be "good".
Analysis — C. Recycled Numbers
Many contestants got stuck in this problem because of the sample test case number 4. Let's say n is 1212, then after moving 1 or 3 digits you will get 2121, hence the pair (1212, 2121) will be counted twice if you count all possible moves. You can avoid this by breaking out of the loop once you reach the original number again, which will happen after moving 2 digits in the above example.
For the small input you can simply check for each pair (n, m), A ≤ n < m ≤ B, whether it satisfies the conditions mentioned in the problem statement, and whether you can obtain m by moving some digits from the back of n to the front without changing their order. To check if you can obtain m from n simply try to move all possible groups of digits from n and check if what you get is m. The digit shifting can be done using string manipulation or mathematical expressions, both will run within the time limit.
But the previous solution will not run within the time limit for the large test cases. So here is another solution which should run within the time limit. For each number n, A ≤ n ≤ B, try to move all possible groups of digits from its back to its front and check if the resulting number satisfies the conditions or not. If it does satisfy the conditions then increment the result. Don't forget to avoid counting the same number twice.
Here is a sample solution:
int solve(int A, int B) {
int power = 1, temp = A;
while (temp >= 10) {
power *= 10;
temp /= 10;
}
int result = 0;
for (int n = A; n <= B; ++n) {
temp = n;
while (true) {
temp = (temp / 10) + ((temp % 10) * power);
if (temp == n)
break;
if (temp > n && temp <= B)
result++;
}
}
return result;
}
Analysis — D. Hall of Mirrors
To keep things exciting, we ended the qualification round with Hall of Mirrors: a truly challenging problem. It is difficult to see how to get started, and then it is even more difficult to actually get the implementation right!
How To Understand Mirrors
The first step in solving this problem is reducing the set of all light ray angles to something that you can actually check. And to do that, it is helpful to use a famous trick for thinking about mirrors. Look at the two diagrams below. Do you see why they are really illustrating the exact same thing?
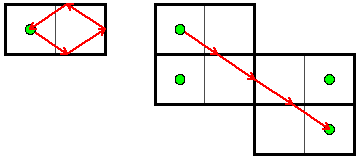
In the left picture, there is a light ray in a 2x1 room that reflects off three mirrors, and then ends back where it started. Let's focus on where the light ray reflects off the bottom mirror. Instead of drawing the reflected light ray, let's take the entire room, and draw it reflected about this mirror. We can then draw the rest of the light ray's path in this picture. This is illustrated in the left diagram below:
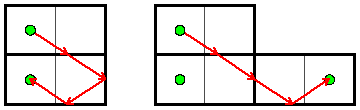
Next, once the light ray hits the right mirror, we can again draw the entire room reflected about that mirror, and then continue drawing the rest of the path there. Finally, we can do the same thing for the one remaining mirror to get the original picture from above. This kind of drawing has two really nice properties for us:
- The light ray is perfectly straight, and it never bends or turns.
- No matter how many reflections we do, and no matter where they are, the reflected position of your starting point will always be in the middle of some square.
The Small Input
If you get this far, you can either try to solve just the small input or both the small and the large. The small input isn't that much smaller really, but it is simpler because you cannot have mirrors in the middle of rooms. This means that we can take the original room and repeatedly reflect it about each of the four walls to cover the whole plane. This is shown below:
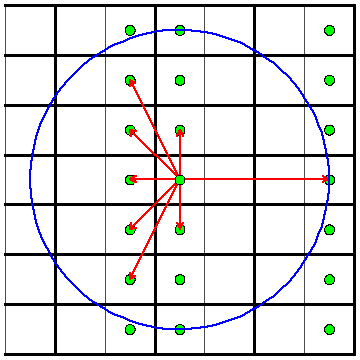
Now let's look at your position in each of these reflected rooms. We claim that these give precisely the directions you can look in order to see a reflection of yourself. Try tracing through a few cases and you will see why.
So to solve the problem, you can iterate over all of these positions that are within distance D of you, and count how many unique directions they give. (Remember that the light ray stops once it returns to you, so if two reflections are in precisely the same direction, only one is visible.)
The Large Input
The large input is not any harder conceptually, but you will have to do some more implementation. The idea is to iterate over all squares within distance D of your starting location, and to follow light rays that are directed towards each of these squares. In particular, how many of these light rays return to the starting position after distance D? The challenge of following rays through a 2-dimensional grid is called "ray casting", and solving it efficiently was the key to Wolfenstein 3D and other games of that era.
This isn't too hard in theory, but the implementation can get nasty if you do not set things up carefully. One approach that helps is to first focus on rays that are moving more vertically than they are horizontally. Then, iterate over each horizontal line the ray touches. Between each of these steps, it will touch 0 or 1 vertical lines, making the processing fairly straightforward (except for corners!).
If you are stuck, try looking through the submitted solutions.