Google Code Jam Archive — Round 3 2011 problems
Overview
At the start of Round 3, a few contestants glanced at the picture of a polygon in problem A and immediately jumped to problem D instead. The first few submissions were brute force solutions to D-small. Problem A, however, turned out not to be as scary as it looked, and acrush took an early lead by solving it in under 10 minutes.
A large number of contestants chose to start with problem B instead, and omeometo went for problem C. For quite some time, he remained the only one to have solved C correctly.
At the 30 minute mark, nika, andrewzta, vepifanov, KennyHORROR, zyz915 and acrush held the top 6 spots with solutions to both A and B. Forty minutes into the contest, everyone in the top 25 had correctly solved two problems. No one had three yet, although winger had A and C instead of A and B, which held him in first place.
Just short of one hour into the competition, nika became the first contestant to solve three problems correctly. He had also already had D-small at that point, which gave him a commanding, 22-point lead over Gennady.Korotkevich, who was in second place despite a failed B-large. Of course, he probably did not know that at the time.
More and more solutions to problem C continued to come in, but with less than an hour left to go there were still no attempts on D-large. With 45 minutes left to go, the top 25 contestants all had 69 points, which meant having solved everything except for D-large, and there were still no attempts at the fiendishly difficult problem.
In the end, only linguo managed to solve D-large, earning him a well-deserved first place. He went with Python this time instead of choosing a more esoteric language.
Congratulations to the top 25. We hope to see you in Tokyo!
Cast
Problem A. Irregular Cakes Written and prepared by Jorge Bernadas Saragoza.
Problem B. Dire Straights Written by Patrick Nguyen and David Arthur. Prepared by Tomek Czajka.
Problem C. Perpetual Motion Written by David Arthur. Prepared by Luka Kalinovcic.
Problem D. Mystery Square Written by David Arthur. Prepared by David Arthur and Petr Mitrichev.
Contest analysis by Jonathan Calhoun, Luka Kalinovcic and David Arthur.
Solutions and other problem preparation by Yiming Li, David Arthur, Igor Naverniouk, Luka Kalinovcic, Tomek Czajka, John Dethridge, Patrick Nguyuen, Petr Mitrichev, Md. Arifuzzaman Arif, Jorge Bernadas Saragoza and Onufry Wojtaszczyk.
A. Irregular Cakes
Problem
Mary the Mathematician has a bakery that she founded some years ago, but after all this time she has become bored with always baking the same rectangular and circular cakes. For her next birthday, she wants to bake an irregular cake, which is defined as the area between two "polylines" between x=0 and x=W. These polylines will be called the lower boundary and the upper boundary.
Formally, a polyline is defined by a sequence of points (P0, P1, ..., Pn) going from left to right. Consecutive points are connected to form a sequence of line segments, which together make up the polyline.
Today is Mary's birthday and she has baked an irregular cake bounded by two polylines with L points and U points respectively. After singing "Happy Birthday," she wants to make G-1 vertical cuts to split the cake into G slices with equal area. She can then share these cake slices with all her guests. However, the irregular cake shape makes this task pretty tricky. Can you help her decide where to make the cuts?
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case begins with a line containing four integers: W (the cake's width), L (the number of points on the lower boundary), U (the number of points on the upper boundary) and G (the number of guests at the party).
This is followed by L lines specifying the lower boundary. The i-th line contains two integers xi and yi, representing the coordinates of the i-th point on the lower boundary. This is followed by U more lines specifying the upper boundary. The j-th line here contains two integers xj and yj, representing the coordinates of the j-th point on the upper boundary.
Output
For each test case, output G lines. The first line should be "Case #x:" where x is the case number (starting from 1). The next G-1 lines should contain the x-coordinates at which cuts must be made, ordered from the leftmost cut to the rightmost cut.
Answers with a relative or absolute error of at most 10-6 will be considered correct.
Limits
1 ≤ T ≤ 100.
1 ≤ W ≤ 1000.
2 ≤ L ≤ 100.
2 ≤ U ≤ 100.
All coordinates will be integers between -1000 and 1000, inclusive.
The x-coordinate of the leftmost point of both boundaries will be 0.
The x-coordinate of the rightmost point of both boundaries will be W.
Points in the same boundary will be sorted increasingly by x-coordinate.
Points in the same boundary will have different x-coordinates.
The lower boundary will always be strictly below the upper boundary for all x between 0 and W, inclusive. (In other words, the lower boundary will have a smaller y-coordinate than the upper boundary at every x position.)
Memory limit: 1GB.
Small dataset (Test set 1 - Visible)
2 ≤ G ≤ 3.
Time limit: 30 seconds.
Large dataset (Test set 2 - Hidden)
2 ≤ G ≤ 101.
Time limit: 60 seconds.
Sample
2 15 3 3 3 0 6 10 8 15 9 0 10 5 11 15 13 8 3 4 2 0 2 5 4 8 3 0 5 3 4 4 7 8 5
Case #1: 5.000000 10.000000 Case #2: 4.290588
B. Dire Straights
Problem
You are playing a card game, where each card has an integer number written on it.
To play the game, you are given some cards — your hand. Then you arrange the cards in your hand into straights. A straight is a set of cards with consecutive values; e.g. the three cards {3, 4, 5}, or the single card {7}. You then receive a number of dollars equal to the length of the shortest straight. If you have no cards, you can form no straights, so you get zero dollars.
You will be given a series of test cases, each of which describes the cards you will have in your hand. Find the maximum number of dollars you can receive for each test case.
Input
The first line of the input contains the number of test cases, T. Each test case consists of one line. Each line contains N, the number of cards in your hand, followed by N integers giving the numbers on those cards. These numbers are all space-separated.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is the maximum number of dollars you can receive.
Limits
1 ≤ T ≤ 100
The numbers on the cards are between 1 and 10000.
Memory limit: 1GB.
Small dataset (Test set 1 - Visible)
0 ≤ N ≤ 10
Time limit: 30 seconds.
Large dataset (Test set 2 - Hidden)
0 ≤ N ≤ 1000
Time limit: 60 seconds.
Sample
4 10 1 2 3 4 5 10 9 8 7 6 8 101 102 103 104 105 106 103 104 0 5 1 2 3 4 9
Case #1: 10 Case #2: 4 Case #3: 0 Case #4: 1
In case 1, you have ten cards numbered 1 to 10, so you make one straight of length 10, and get 10 dollars.
In case 2, you could make two straights {101,102,103,104,105,106} and {103,104} and get 2 dollars. But it would be better to make {101,102,103,104} and {103,104,105,106} and get 4 dollars.
In case 4, the card with the number 9 must be in a straight containing only that card. So you get 1 dollar.
In case 3, you have zero cards, so you get zero dollars. You don't get money for nothing.
C. Perpetual Motion
Problem
Have you ever been to the Google Lemming Factory? It is a very unusual place. The floor is arranged into an R x C grid. Within each grid square, there is a conveyor belt oriented up-down, left-right, or along one of the two diagonals. The conveyor belts move either forwards or backwards along their orientations, and you can independently choose which of the two possible directions each conveyor belt should move in.
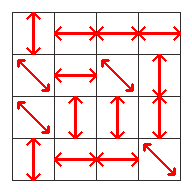
Currently, there is a single lemming standing at the center of each square. When you start the conveyor belts, each lemming will move in the direction of the conveyor belt he is on until he reaches the center of a new square. All these movements happen simultaneously and take exactly one second to complete. Afterwards, the lemmings will all be on new squares, and the process will repeat from their new positions. This continues forever, or at least until you turn off the conveyor belts.
- When a lemming enters a new square, he continues going in the direction he was already going until he reaches the center of that square. He will not be affected by the new conveyor belt until the next second starts.
- If a lemming moves off the edge of the grid, he comes back at the same position on the opposite side. For example, if he were to move diagonally up and left from the top-left square, he would arrive at the bottom-right square. By the miracle of science, this whole process still only takes 1 second.
- Lemmings never collide and can always move past each other without difficulty.
Here are two ways of assigning directions to each conveyor belt from the earlier example:
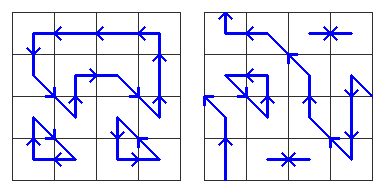
In both cases, we avoid ever sending two lemmings to the center of the same square at the same time.
Given an arbitrary floor layout, calculate N, the number of ways to choose directions for each conveyor belt so that no two lemmings will ever end up in the center of the same square at the same time. The answer might be quite large, so please output it modulo 1000003.
Input
The first line of input gives the number of test cases, T. T test cases follow. Each begins with a line containing positive integers R and C.
This is followed by R lines, each containing a string of C characters chosen from "|-/\". Each character represents the orientation of the conveyor belt in a single square:
- '
|' represents a conveyor belt that can move up or down. - '
-' represents a conveyor belt that can move left or right. - '
/' represents a conveyor belt that can move up-right or down-left. - '
\' represents a conveyor belt that can move up-left or down-right.
Output
For each test case, output one line containing "Case #x: M", where x is the case number (starting from 1), and M is the remainder when dividing N by 1000003.
Limits
1 ≤ T ≤ 25.
Memory limit: 1GB.
Small dataset (Test set 1 - Visible)
3 ≤ R ≤ 4.
3 ≤ C ≤ 4.
Time limit: 30 seconds.
Large dataset (Test set 2 - Hidden)
3 ≤ R ≤ 100.
3 ≤ C ≤ 100.
Time limit: 60 seconds.
Sample
3 3 3 |-/ ||| --| 3 4 ---- |||| \\// 4 4 |--- \-\| \||| |--\
Case #1: 2 Case #2: 0 Case #3: 16
D. Mystery Square
Problem
I have written down a large perfect square in binary, and then replaced some of the digits with question marks. Can you figure out what my original number was?
Input
The first line of the input gives the number of test cases, T. T test cases follow, one per line. Each line contains S: a perfect square written in binary, but with some of the digits replaced by question marks.
Output
For each test case, output one line containing "Case #x: N", where x is the case number (starting from 1) and N is a perfect square written in binary, obtained by replacing each '?' character in S with either a '0' character or a '1' character.
Limits
1 ≤ T ≤ 25.
S begins with '1'.
S contains only the characters '0', '1', and '?'.
In every test case, there is exactly one possible choice for N.
Memory limit: 1GB.
Small dataset (Test set 1 - Visible)
S is at most 60 characters long.
S contains at most 20 '?' characters.
Time limit: 30 seconds.
Large dataset (Test set 2 - Hidden)
S is at most 125 characters long.
S contains at most 40 '?' characters.
Time limit: 60 seconds.
Sample
3 1??? 1 10??110??00??1000??
Case #1: 1001 Case #2: 1 Case #3: 1011110110000100001
Analysis — A. Irregular Cakes
Before we can start solving the problem, we first need to know how to calculate the area of the cake, so we know how much cake each party-goer is going to eat. We are guaranteed that this is a non-intersecting polygon in the limits, so we can use the equation:
2*Area = sum(Xi * Yi+1 - Xi+1 * Yi) for i = 0 to N-1.
For this to work the first and last points in the polygon must be the same point. That is, X0 = XN and Y0 = YN. The list of points must also be in counterclockwise order. This can be achieved by iterating over all points in L, and then iterating over all points in U in reverse order.
Once we know the total area of the cake, we need to determine how much cake to give each guest. Since there are G guests, we can evenly calculate this number as AreaPerGuest = Area / G.
Finally we are ready to determine where to cut the cake. This can be solved a variety of ways, but here we will discuss using a binary search as this is often the simplest algorithm to code. To obtain a piece of cake with an area of AreaPerGuest, we know that the vertical cut will have an X coordinate between 0 and W, so we do a binary search over this range. For each cut point we try during the search, we compute the area of the cake to the left of that cut. If it produces a piece of cake with area greater than AreaPerGuest, we update the upper bound of our search. If we choose a cut that produces a piece of cake with area less than or equal to AreaPerGuest, we update the lower bound of our search. This search will eventually converge to the correct cut point with sufficient accuracy.
If G=2, then we are done. If G > 2, then the binary search can be repeated to find the other cuts. The second cut point should be placed such that the area of cake to the left of that cut is AreaPerGuest * 2, the third cut point should be placed so that the area of cake to the left of that cut is AreaPerGuest * 3, and so on.
At each iteration of the binary search, we need to calculate the area of a polygon using part of L, U, and a line on an arbitrary X coordinate, which requires more work than computing the area of the whole cake. The first thing to note is that we can use all points in L and U that have X coordinates such that 0 <= Xi <= Xcut, where Xi is the X coordinate of point i, and Xcut is the X coordinate of the cut. Next we need to determine the Y coordinates of our Xcut points on L and U. If we find two consecutive points A and B in L such that Ax <= Xcut and Bx >= Xcut, we can use line intersection to find the intersection of line AB and the vertical line defined by Xcut. Once we know these two new points the area of the cut piece of cake can be calculated.
This problem can also be solved with a linear time solution in O(N+G). The basic premise is to split the cake into trapezoids, and iterate from left to right accumulating the total area. Any time a trapezoid needs to be split for a cut, a quadratic equation is used to determine where to cut the cake. This approach only requires the basic formula for the area of a trapezoid, which is (a+b)/2 * h, where a and b are the lengths of the bases, and h is the height of the trapezoid.
More information:
Polygon area
Binary search
Analysis — B. Dire Straights
Dire Straights had one of the easiest small datasets for round 3. Several brute force or backtracking solutions that followed the rules could come up with a valid answer in the allotted time, so rather than look at the small dataset, we will instead examine the large. The large dataset requires some insight into a greedy approach.
For a problem like this, a good strategy is to think of how you might try to solve this problem by hand. A very intuitive strategy is to first put all the cards in order, then start setting the cards down on the table, creating a new straight whenever necessary. Since our goal is to make the length of the shortest straight as long as possible, then one idea that seems like it might work is to always increase the length of the shortest straight when we have a choice. Now we need only to prove that this choice is optimal.
Suppose we have two straights, one from a to b, another from c to d, such that a < c <= d < b.
a-------b
c-----d
Notice that we can replace these two straights with straights from a to d and c to b (this change is illustrated below), and this does not decrease the score. In fact, this change has the potential to increase the score.
a------d
c------b
This shows that we can always make sure that a straight that started later never ends before one that started earlier. Hence, attaching the next card to the shortest straight is optimal.
Finally, the size of every straight is examined and the length of the shortest straight is the total score achieved in Dire Straights.
Analysis — C. Perpetual Motion
The first thing we need to notice is that if two lemmings do not end up in the same square after one second, they will never end up in the same square. That is because after one second there will be exactly one lemming in each square, and the state is exactly the same as the second before.
The number of combinations for the conveyor belt directions is 2R·C, so we can afford to try all of them to solve the easy input and count how many combinations lead to all lemmings being in different squares after one second.
To solve the hard input, we'll have to take a look at the problem from a graph theory perspective. Suppose we created a bipartite graph like this:
- For each cell (r, c), create two nodes startr, c and endr, c.
- Create an edge between startr1, c1 to endr2, c2 if there is a way to choose the direction of the conveyor belt in cell (r1, c1) such that the lemming ends up in (r2, c2) after one second.
All start nodes will end up being incident to exactly two edges because there are exactly two different cells where a lemming can end up in one second starting from any given cell. End nodes, on the other hand, can be incident to 0-8 edges, depending on the conveyor belt orientations of the neighbouring cells.
Let's observe the graph some more. There are two rules that apply:
- If there are no edges incident to a node endr, c then no lemming can end up in cell (r, c) in one second, so there will be two lemmings in some other cell no matter how we direct the conveyor belts. In that case the answer is simply 0, so we can proceed to the next test case.
- If there is a node endr2, c2 incident to only one edge leading to startr1, c1 then we have no other choice but to direct the conveyor belt on the cell (r1, c1) to lead to the cell (r2, c2). Then we can simply remove both endr2, c2 and startr1, c1 from the graph along with all the incident edges.
We can apply these rules iteratively until they can not be applied anymore.
Let N be the number of start nodes left after the above process is done. The number of end nodes is also equal to N, because we removed them in pairs.
The number of edges incident to each start node is still equal to two, so total the number of edges is equal to 2·N because the graph is bipartite. We also know that each end node is now incident to at least two edges, because the above rules do not apply anymore.
But, if any of the end nodes had more than two incident edges then the number of edges incident to all the end nodes combined would be greater than 2·N. This would contradict the fact that the number of edges is equal to 2·N. Therefore, the number of edges incident to each end node is also equal to two.
Any graph having all node degrees equal to two is in fact a set of cycles. For bipartite graphs, the length of each cycle is even. So, we are left with K cycles of even length which we can solve independently and multiply the individual numbers to get the final number.
To solve the circle, select any cell (r1, c1) and pick a conveyor belt direction. The lemming ends up in (r2, c2). Now remove startr1, c1 and endr2, c2 from the graph along with incident edges. This will break up the cycle, and we can proceed to apply rule #2 until we decide the conveyor belt for all the remaining cells. Because the cycle has even length and we always remove nodes in pairs, the rule #1 will never apply.
We can pick the direction of the cell (r1, c1) in two ways. So the answer for any cycle is always 2. So the final answer is equal to 2K (modulo 1000003).
Analysis — D. Mystery Square
This problem may have a simple statement, but make no mistake: it is really hard. Unless you have a small army of computers working in parallel, there is no way to try all 240 possible values. You need a way to limit your search.
The key observation is that for the most part, a perfect square is uniquely determined by both the first half of its digits, and by the second half. Either one suffices. So the high-level idea is to pick the half that has fewer question marks in it, try all possible ways of filling the question marks, deduce what the rest of the number has to be, and then see if it works. Before we get into the details though, let's talk about one nasty little implementation detail that you can't help but notice.
Dealing with big integersIf a binary number has 120 digits, there is obviously no way to fit it into a standard 64-bit integer! And that means arithmetic can be a nuisance. Here are a few ways you can deal with this extra complication:
- Use Java and take advantage of the BigInteger class.
- In g++, you can use the little known __uint128_t type.
- Roll your own BigInteger functions for 128 bits. In practice you only need Square and SquareRoot. The first is doable with grade-school long multiplication formulas and some care. The second can be done with a binary search.
- Use an external library such as GMP.
Hopefully you remembered your Fair Warning from last year, and were prepared! Even so, we would have loved to let you work on only 64-bit integers if we could, but it turns out computers are so fast today that you can simply loop over ALL 64-bit perfect squares in a few seconds. The problem becomes pretty boring in that case.
Filling in a perfect square top-downAll right, so with that detail of the way, let's get down to the solution. If you know the first half of the digits in a perfect square, how can you easily figure out the rest? For example, let's look at 10110????? (in binary).
Notice the square root has to be at least sqrt(1011000000) and at most sqrt(1011011111). In fact, there is only one integer that is between these two, and it is 11011! So we can just see if 110112 matches 10110?????, and then we're done. And this always works. If a number X has 2t digits, then its square root Y has t digits, and (Y+1)2 = Y2 + 2Y + 1, which already differs from Y2 in more than the last t digits.
So in summary: once we know the first half of the digits in N, we can just replace the ? characters with 1, take the square root, round down, and that is the only possible option.
Filling in a perfect square bottom-upThe other half of the solution is not much harder conceptually, but the devil is in the details. If you know the second half of the digits in a perfect square, how can you easily figure out the rest? For example, let's look at ????011001.
Getting started is actually tricky, but let's suppose we have figured out the last two binary digits of the square root are 01.
- The square root must then be 4A + 1 for some integer A. Its square is 16A2 + 8A + 1 = 8A + 1 mod 16. However, we know that the square is 9 mod 16, and hence A must be odd. Therefore, the square root must end in 101.
- We now know the square root must be 8B + 5 for some integer B. Its square is then 64B2 + 80B + 25 = 16B + 25 mod 32. However, we know that the square is 25 mod 32, and hence B must be even. Therefore, the square root must end in 0101.
- Continuing in this way, we can use the last k+1 digits of N to calculate the last k digits of its square root. If you know just over half of the digits in N, this is enough to completely determine the square root. As above, we can now just check if it works, and then we're done.
This technique always works, subject to two condition: (a) N must be odd, and (b) you must already know the last two digits of the square root. You might enjoy writing down the formula in both failure cases, and seeing what goes wrong.
Let's think about (b) first. If N is odd, then the square root must also be odd, and so the last digit must be 1. There is no easy way to determine what the second last digit has to be in advance, but who cares? Just try both of them, and see which one works!
Next let's suppose N is even. Since it is a perfect square, it must actually be a multiple of 4, and N/4 is also a perfect square. So we can just cut the last two digits off of N, repeat until N becomes odd, and then solve as above. In fact, this trick is pretty much required. If N is odd, then the last k digits are enough to find k-1 digits in the square root. If N is even though, then the last k digits may only be enough to find k/2 digits in the square root.
Of course, we might not know whether N is even or odd in advance. If the last digit is a '?' character, then we just try both possibilities and see what happens.
Remark: This whole approach works only because 2 is prime. If we were working base-10, then an even number that is not a multiple of 10 would be pretty nasty to deal with!
Putting it all togetherHere is the full solution:
- Assume that N is odd, if possible.
- If N has more question marks in its bottom half than in its top half, then iterate over all possible ways of filling in the top half question marks, deduce the whole number, and see if it works.
- If N has more question marks in its top half than in its bottom half, then iterate over all possible ways of filling in the bottom half question marks, deduce the whole number, and see if it works.
- Now assume that N is even, if possible. Fill in the last two digits as zero, and repeat from the very beginning (potentially solving either top-down or bottom-up) for N/4.
The parenthetical comment in the last part is actually quite important! Consider the following input for example: "10010000010000011100000110110010001???????????????????????????????????000000000??000000000000000?0000000000000000000000??00". Most of the '?' characters are in the first half, so it is tempting to just start from the back and never re-evaluate your decision. However, there are only '0' characters back there, and they will not give you much information. To run fast enough in this case, you need to start from the front after eliminating some of the 0's.