Google Code Jam Archive — World Finals 2010 problems
Overview
This was our most difficult round ever. Two problems, E and F, remained unsolved in the end -- a floating point geometry problem and a tricky backtracking problem.
marek.cygan put the first entry onto the scoreboard just under 14 minutes into the competition with a correct submission of B-small. The rest of the round was a turbulent race, with many re-orderings of the top 5.
For the first 47 minutes of the competition, two-time defending champion ACRush had no submissions. He seemed to be looking at the screen, writing something on paper, but not typing. At 47m13s, he submitted a correct solution to C-small and quickly followed that 3 minutes later with a correct submission to D-small, making his presence in the top 10 known to all.
By this point, it had become clear that B was the most tractable problem of the round. Every one of the top 10 finishers ended up solving B, D and A-small. Nine of the top ten contestants solved C. The top 5 spots ended up being decided based on A-large, E-small and F-small.
At the 2h28m mark, earl became the first contestant to crack open problem E. One minute later, ACRush solved E-small as well and moved into the top spot for the next four minutes, until Egor solved D and took the #1 spot away from ACRush.
Egor ended up winning the title of Code Jam 2010 Champion with a definitive 11-point lead over 2nd-placed krijgertje. Burunduk1 took 3rd place, having been the only contestant to solve F-small correctly, which gave him a 6-point lead over ACRush, who finished in 4th. In 5th was marek.cygan, with B, C, D and A-small.
The last few minutes of the round saw a flurry of 11 submissions from ACRush on F-small, all incorrect. In total, 6 contestants solved E-small, but none of their solutions could pass E-large, which required one to detect and short-circuit loops in the ninja's rope. Although Egor and Eryx attempted E-large during the last minute, both of their solutions timed out.
Congratulations to all of the competitors. We hope to see you back next year.
Cast
Problem A. Letter Stamper Written by Cosmin Negruseri. Prepared by Xiaomin Chen and David Arthur.
Problem B. City Tour Written by Cosmin Negruseri. Prepared by David Arthur and Ante Derek.
Problem C. Candy Store Written by Bartholomew Furrow. Prepared by David Arthur and Bartholomew Furrow.
Problem D. Travel Plan Written by Cosmin Negruseri. Prepared by Petr Mitrichev.
Problem E. Ninjutsu Written by Igor Naverniouk and Junbin Teng. Prepared by Igor Naverniouk, Bartholomew Furrow, Tomek Czajka, and Derek Kisman.
Problem F. The Paths of Yin Yang Written by Xiaomin Chen. Prepared by Xiaomin Chen, David Arthur, and Derek Kisman.
Contest analysis presented by David Arthur, Xiaomin Chen, Derek Kisman, Igor Naverniouk, and Cosmin Negruseri.
Solutions and other problem preparation provided by Marius Andrei and John Dethridge.
A. Letter Stamper
Problem
Roland is a high-school math teacher. Every day, he gets hundreds of papers from his students. For each paper, he carefully chooses a letter grade: 'A', 'B' or 'C'. (Roland's students are too smart to get lower grades like a 'D' or an 'F'). Once the grades are all decided, Roland passes the papers onto his assistant - you. Your job is to stamp the correct grade onto each paper.
You have a low-tech but functional letter stamp that you use for this. To print out a letter, you attach a special plate to the front of the stamp corresponding to that letter, dip it in ink, and then apply it to the paper.
The interesting thing is that instead of removing the plate when you want to switch letters, you can just put a new plate on top of the old one. In fact, you can think of the plates on the letter stamp as being a stack, supporting the following operations:
- Push a letter on to the top of the stack. (This corresponds to attaching a new plate to the front of the stamp.)
- Pop a letter from the top of the stack. (This corresponds to removing the plate from the front of the stamp.)
- Print the letter on the top of the stack. (This corresponds to actually using the stamp.) Of course, the stack must actually have a letter on it for this to work.
Given a sequence of letter grades ('A', 'B', and 'C'), how many operations do you need to print the whole sequence in order? The stack begins empty, and you must empty it when you are done. However, you have unlimited supplies of each kind of plate that you can use in the meantime.
For example, if you wanted to print the sequence "ABCCBA", then you could do it in 12 operations, as shown below:
|
Operation |
Printed so far |
Stack |
0. -
|
-
|
-
|
Input
The first line of the input file contains the number of cases, T. T test cases follow, one per line. Each of these lines contains a single string S, representing the sequence of characters that you want to print out in order.
Output
For each test case, output one line containing "Case #x: N", where x is the case number (starting from 1) and N is the minimum number of stack operations required to print out S.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
S is a non-empty string containing only the letters 'A', 'B', and 'C'.
Small dataset (Test set 1 - Visible)
1 ≤ T ≤ 100.
S has at most 100 characters.
Large dataset (Test set 2 - Hidden)
1 ≤ T ≤ 20.
S has at most 7000 characters.
Sample
2 ABCCBA AAABAAB
Case #1: 12 Case #2: 13
B. City Tour
Problem
During summer time, old cities in Europe are swarming with tourists who roam the streets and visit points of interest.
Many old cities were built organically and not according to some architecture plan, but, strangely, their growth exhibits a similar pattern: the cities started from three points of interest, with each pair being connected by a bidirectional street; then, gradually, new points of interest were added. Any new point of interest was connected by two new bidirectional streets to two different previous points of interest which were already directly connected by a street.
A tourist visiting such a city would like to do a tour visiting as many points of interest as possible. The tour can start at any point of interest and must end at the same point of interest. The tour may visit each street at most once and each point of interest at most once (with the exception of the first point of interest which is visited exactly twice).
You are given the description of how the city grew. Find the largest number of different points of interest a single tour can visit in this city.
Input
The first line of the input file contains the number of cases, T. T test cases follow.
Each case begins with the integer N - the total number of points of interest in the city. Points are denoted with numbers from 1 to N; numbers 1, 2, and 3 denote the three original points when the city started, while numbers 4, ..., N denote the other points in the order they were added to the city.
The next N-3 lines each contain a pair of space-separated integers A, B, indicating that the corresponding point of interest was connected by streets to points A and B. First of these lines corresponds to point number 4, second to point number 5, etc.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is the largest number of points of interest a tour can visit in this city.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 50.
Small dataset (Test set 1 - Visible)
4 ≤ N ≤ 15.
Large dataset (Test set 2 - Hidden)
4 ≤ N ≤ 1000.
Sample
2 5 1 2 2 1 6 1 2 1 4 4 5
Case #1: 4 Case #2: 6
C. Candy Store
Problem
Owning a candy store is tough! You have to optimize all kinds of things. Lately you've been selling a very popular kind of candy called Whizboppers. These candies become rotten very quickly, which gives them the following properties:
- You must buy new Whizboppers from your supplier every morning.
- You must sell Whizboppers in the boxes you bought from your supplier that morning.
Every day up to k people visit your store, and, starting from the first person, they will choose an integer number of cents to spend on Whizboppers: between 1 and C cents inclusive. You're going to sell Whizboppers for 1 cent per gram; so if a person wants to spend 4 cents, you will give that person exactly 4 grams of candy. You might do this by giving the person a 4-gram box, or perhaps a 2-gram box and two 1-gram boxes.
What is the minimum number of boxes you need to order so that, no matter what amount each person orders, you can always give all of the people the mass of Whizboppers they want?
Note: When a person chooses how much candy to buy, you know what other people have already bought, but you don't know what future people will buy.
For example, if up to 2 people visit your store every day, and they spend up to 2 cents each (k=2, C=2), you could buy four 1-gram boxes from your supplier. But you can do better: if you buy two 1-gram boxes and one 2-gram box, you can satisfy your customers. Here's how:
First Person Boxes given Second Person Boxes given
--------------------------------------------------------
2 cents 1 x 2-gram 2 cents 2 x 1-gram
1 cent 1 x 1-gram
-----------------------------------------------------
1 cent 1 x 1-gram 2 cents 1 x 2-gram
1 cent 1 x 1-gram
Regardless of what the first person orders, you can give out boxes so that the second person can still get the right amount of candy. So for k=2, C=2, you can serve any sequence of orders with 3 boxes.
Input
The first line of the input gives the number of test cases, T. T lines follow, each of which contains two integers: k and C, the maximum number of people and the maximum number of cents each person may spend.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is the minimum number of boxes you need to order every day.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 100.
Small dataset (Test set 1 - Visible)
1 ≤ k ≤ 20.
1 ≤ C ≤ 3.
Large dataset (Test set 2 - Hidden)
1 ≤ k ≤ 1000.
1 ≤ C ≤ 1012.
Sample
4 1 5 2 2 10 3 2 50
Case #1: 3 Case #2: 3 Case #3: 19 Case #4: 11
Explanation
In the first case, you can buy one 1-gram box and two 2-gram boxes. In the second case, you can buy two 1-gram boxes and one 2-gram box.
D. Travel Plan
Problem
In a yet-to-be-announced and rechecked discovery by Antarctic astronomers, it is written that there are N inhabited planets in space, all lying along the same straight line, with the i-th planet lying at coordinate Xi along the line (i = 1, 2, ..., N). Earth is the first planet, lying at coordinate zero, so X1 will always be equal to 0.
Being very excited about this fact, you start planning a trip to visit all the planets. Since unknown planets can be dangerous, you want to visit each planet exactly once before returning to Earth. You have F units of fuel, and you want to spend as much of it on this trip as possible so that your final landing on Earth is safer. Your spaceship is pretty basic and can only fly along a straight line from any planet i to any other planet j, consuming |Xi-Xj| units of fuel along the way. It can't turn without landing.
So you need to create a travel plan that requires at most F units of fuel, starts from Earth, visits each of the other planets exactly once, and then returns to Earth. If there are several such plans, you should find the one that consumes most fuel. Output the amount of fuel consumed.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case description starts with a line containing the number of planets N. The next line contains N numbers Xi, the coordinates of the planets. The next line contains the amount of fuel F that you have.
Output
For each test case, output one line containing either "Case #x: NO SOLUTION", when there's no such travel plan, or "Case #x: y", where x is the case number (starting from 1) and y is the maximum amount of fuel consumed.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
1 ≤ F ≤ 1017.
-1015 ≤ Xi ≤ 1015.
X1=0.
All Xi are different.
Small dataset (Test set 1 - Visible)
1 ≤ T ≤ 100.
2 ≤ N ≤ 10.
Large dataset (Test set 2 - Hidden)
1 ≤ T ≤ 20.
2 ≤ N ≤ 30.
Sample
3 3 0 10 -10 40 5 0 1 2 3 4 13 5 0 1 2 3 4 7
Case #1: 40 Case #2: 12 Case #3: NO SOLUTION
E. Ninjutsu
Problem
Ninjutsu is the martial art of the mysterious Japanese assassins, ninja. As a beginner in the practice of ninjutsu, your first task is to master the use of the grappling hook.
A grappling hook is a technologically-advanced device consisting of a hook tied to some (very strong and very thin) rope. Proper use of a grappling hook involves throwing the hook at a target and hoping that it catches.
This time, it did! You are now hooked onto a target that is located at (0,
0). Your rope extends to the left, and you're at the end of it; when you jump,
you will start swinging counter-clockwise around the target. There are other
targets located to the right and above (0, 0), at (xi,
yi)) with
Your rope currently has length R, but you may choose to cut it down to
any shorter length r (including non-integers) before you start swinging.
As such, you will start at
What is the maximum number of bends you can put into the rope with one swing? A bend happens when your rope touches a target and then rotates some non-zero number of degrees around that target. The rope will always remain perfectly straight (again, this is possible because you are a ninja), except at bends.
Example

In the example above, there are 6 points:
- (0, 0),
- (3, 1),
- (12, 4),
- (14, 5),
- (13, 7), and
- (7, 10).
If, however, you cut the rope by 0.18 units, you will not have enough
length to reach point
(0, 0)--(12, 4)--(14, 5)--(13, 7)--(12, 4)--(14, 5)and will end up orbiting point
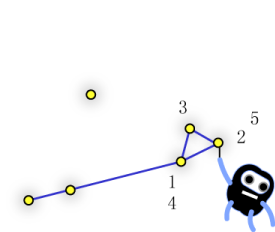
Case #1 in the sample input below represents this example.
Input
The input will start with a line containing T, the number of test cases to follow. Each test case will start with two integers together on a line: N and R. The next N lines will each contain a pair of integers -- xi and yi -- the coordinates of the targets, starting with the target at (0, 0).
Output
For each test case, output a line of the form "Case #C: k", where C is the 1-based case number, and k is the maximum number of bends that can be made in the rope in one swing.Limits
Time limit: 60 seconds per test set.Memory limit: 1GB.
1 ≤ T ≤ 100
All target coordinates are integers.
All targets will be at different locations.
The first target listed will be located at (0, 0).
There will be at least one value of r that gives an optimal solution and has the property that a rope of length
Small dataset (Test set 1 - Visible)
1 ≤ N ≤ 101 ≤ R ≤ 1,000
0 ≤ xi ≤ 1,000
0 ≤ yi ≤ 1,000
Large dataset (Test set 2 - Hidden)
1 ≤ N ≤ 1,0001 ≤ R ≤ 109
0 ≤ xi ≤ 109
0 ≤ yi ≤ 109
Sample
6 6 24 0 0 3 1 12 4 14 5 13 7 7 10 2 1 0 0 2 0 2 1 0 0 1 0 2 10 0 0 4 0 3 50 0 0 9 0 10 0 3 12 0 0 3 0 3 4
Case #1: 5 Case #2: 0 Case #3: 0 Case #4: 2 Case #5: 12 Case #6: 3
F. The Paths of Yin Yang
So, If and Else grow out of each other;
Hardness and Tractability complete each other;
Long int and Short int shape each other;
High bits and Low bits determine each other;
Music and Voice give harmony to each other;
Push_front and Push_back give sequence to each other.
-- Tao Te Ching, Laozi, Zhou dynasty, ancient China.
Translated (loosely) by yours truly.
Problem
Given an rectangular grid of N rows and M columns, each cell can be labeled black (Yin) or white (Yang). Two cells are neighbors if they share a common unit-length edge segment. The grid is valid if all the black cells form a path, and all the white cells form a path. A path is a set S of cells defined as follows:
- The cells form a connected piece. From each cell in
S, you can reach any other cell inSby moving between neighbors withinS. - Exactly two cells in
Shave exactly one neighbor inSeach. These are the "ends" of the path. - Every other cell in
Shas exactly two neighbors inS.
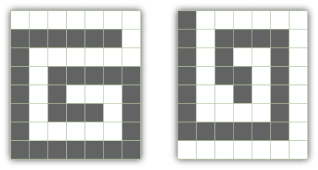
For example, in the picture below, the first grid is valid, while the second grid is not -- although the black cells form a path, the white cells do not.
Given N and M, compute the number of valid grids. Note that symmetry doesn't matter -- as long as two valid grids differ in one position they are considered different, even if one can be rotated or flipped to the other.
Input
The first line of the input will be a single integer T, the number of test cases. T lines follow, each of which contains two integers separated by a space: "N M", as defined above.
Output
For each test case, output a line in the form "Case #x: A", where x is the case number, starting from 1, and A is the number of valid grids of the specified size.
Limits
Memory limit: 1GB.
1 ≤ T ≤ 50
Small dataset (Test set 1 - Visible)
Time limit: 30 seconds per test set.
4 ≤ N, M ≤ 10
Large dataset (Test set 2 - Hidden)
Time limit: 120 seconds per test set.
For 80% of the test cases, 4 ≤ N, M ≤ 50
For 90% of the test cases, 4 ≤ N, M ≤ 70
For all test cases, 4 ≤ N, M ≤ 100
Sample
3 4 4 4 6 5 5
Case #1: 24 Case #2: 44 Case #3: 48
Analysis — A. Letter Stamper
The problem idea originated from the report of one of Robert Tarjan's talks, where a quadratic solution for four letters was claimed. We found the easier three-letter version was already very interesting, and presented it to you as the first problem for this Code Jam final.
We note that the general case where the alphabet size is not restricted to a small constant such as 3 can be solved by dynamic programming in O(n^3). It had appeared in several programming contests before.
The current state is characterized by a pair (S, K), where S is the suffix of the input string you still need to print (so the next letter you need to print is the head of S), and K is the stack. For each situation, we need to decide if the next step is a push, a pop, or a print.
We state some rules that are satisfied by an optimal sequence. These will make the solution quite clear. There can be other optimal sequences, but you can always reduce them to one that satisfies these conditions.
Rule 1. If the first letter of S is the same as the top of K, then the next step is a print.
Rule 2. You never need to push the letter that's already on top of the stack. Therefore no letters appears on the stack twice in a row.
Rule 3. Immediately after you push a letter X, the next step is to print X.
The rules above are trivial and we omit the reasoning. But it might worth spending a little time convincing yourself formally.
Rule 4. There should never be three consecutive letters in the stack of the form XYX.
Let us justify this rule. Suppose an optimal solution has XYX on the stack. Let's modify it. At some point the top of the stack is XY and we were going to push another X. Instead, we will pop the Y. Then we continue as before, until we were going to pop the second X that now doesn't exist. Instead, we will push Y, arriving at the same state as before. This way we have shortened the stack while achieving a solution of the same length. By induction you can keep simplifying the solution until all 4 rules are satisfied.
Rule 4, together with Rule 2, implies that the stack always contains a cycle of 3 letters, e.g. ABCABCABC.... The state of the stack then is completely defined by the first two letters and the stack height. There are only 6 patterns, and the height of the stack is never bigger than n. Hence the number of possible states (S, K) is O(n^2). This gives a quadratic dynamic programming solution.
Analysis — B. City Tour
This proved to be the easiest problem in the finals for the experienced competitors.
We get some insight into the problem by noticing the graph resembles a tree. These graphs are actually called partial 2-trees. We can actually build a tree if we follow the way the graph is constructed. We build another graph that associates a node to each new added cycle of length this cycle shares an edge to an old cycle so we add an edge between the two respective nodes in the second graph. This way we have built the tree decomposition of these graphs. As on trees many problems that are hard to solve on general graphs have polynomial algorithms on this type of graphs.
Let's solve the related problem of finding the longest path in a tree. We can use dynamic programming and depth first search. We mark a node as a root. Every path in the tree has exactly one node that is closest to the root and this node splits the path in two downward paths. Now for each node in the tree we compute the longest downwards path that starts in it. To find the largest path in the tree we look at each node and at the two longest paths that start in it's children. This solves the problem in linear time.
The solution for our original problem is pretty similar. For each edge (x,y), we compute the cycle that contains it and and all the other nodes in the cycle have larger indexes. Let's call this a downward cycle since it goes the opposite direction of where the initial three nodes are. To find that number we have to look at all higher indexed nodes that were connected to this edge and try to use them as intermediary points in the cycle. So for a given intermediary point z we can build a cycle by looking at the longest downward cycle that contains the edge (x,z) and the longest downward cycle that contains the edge (z,y), use all the edges, add edge (x,y) and remove the edges (x,z) and (z,y).
We also compute the largest downward cycle which contains these two nodes but doesn't contain this edge, this is a union of the cycle that goes through these nodes and the second largest path from which we remove the edge (x,y).
And here is some code that does implements this solution:
int best_so_far = 0;
int best(int x, int y, int N, int[][] a) {
int max_len = 2;
int second_max_len = -1;
for (int i = Math.max(x, y) + 1; i < N; i++) {
if (a[x][i] * a[y][i] > 0) {
int len = best(x, i, N, a) + best(y, i, N, a) - 1;
if (len > max_len) {
second_max_len = max_len;
max_len = len;
} else if (len > second_max_len) {
second_max_len = len;
}
}
}
best_so_far = Math.max(max_len, best_so_far);
best_so_far = Math.max(max_len + second_max_len - 2,
best_so_far);
return max_len;
}
Another cool solution is based on the idea of contracting each node of degree two. We replace it with an edge which has the weight equal to the sum of the weights of the two incoming edges. It's a pretty neat idea and we'll let you figure out the details on your own.
Analysis — C. Candy Store
Summary
At first this problem seems intimidating. There are a huge number of ways customers can order, and even once you've decided which boxes to order, verifying that all possible scenarios are covered is non-trivial.
But as it turns out, a greedy algorithm for choosing the boxes, and a greedy approach to handing them out, ends up working! And as with most greedy problems, the difficulty lies only in convincing yourself that it works. It's actually the easiest problem in the set to implement. The only thing you must overcome is self-doubt!
Proof
Suppose that part of our order is a set of boxes with total weight N grams, with no box larger than X = floor(N/k)+1. Furthermore, suppose that we know these boxes have the property that if the k customers' orders don't total more than N grams, these boxes can be used greedily to satisfy their orders. "Greedily" means that when a customer comes to the store, you simply find the largest box that is less than or equal to his order, and give it to him, repeating until you've filled his order exactly. This is our inductive hypothesis: a guarantee that this strategy works.
Now, suppose we order another box with weight X (ie, floor(N/k)+1) grams, making a new set of boxes with total weight N+X grams (and note that no box is larger than floor((N+X)/k)+1, trivially). Suppose the k customers order no more than N+X grams. What happens if we apply the greedy strategy? Well, as soon as we see an order of ≥ X cents, we will use this new X-gram box on it immediately. If we now pretend that the customer instead ordered X fewer cents, then we know the greedy strategy with the rest of the boxes works. The choices made by the strategy are unchanged aside from the use of the new box. If it turns out that there is NO order of ≥ X cents, then the total is at most k*(X-1) ≤ k*(N/k) = N grams. The new box can't ever be used, so the greedy strategy does the same thing for these orders that it did before, and thus it works.
So using induction, we now have what I'll call "The Algorithm", which constructs sets of boxes that work greedily. We start with 0 boxes, and keep adding new boxes of size floor("total sum so far"/k)+1. eg, first we'll add k boxes of size 1 (which we obviously need), then a box of size 2, and so on.
Ok, now how do we prove that this is the best we can do? Suppose we've ordered some set S of boxes that works. Sort the boxes from smallest to largest, and consider the first box that is larger than would be chosen by "The Algorithm" based on all the boxes smaller than it. In other words, if this box is of size Y, and N is the total of all the boxes smaller than it, Y > X = floor(N/k)+1. (Note that X ≤ C since N < k*C.) What happens if the customers all order X cents? None of the boxes of size Y or greater can be used, and the total is k*X > N, so all the boxes smaller than Y don't add up to enough to handle them. This can't possibly work, regardless of strategy.
Thus, every box in S, considered in sequence, is no larger than would be added by "The Algorithm" based on the previous boxes. But if any box chosen is STRICTLY smaller, then "The Algorithm"'s later selections will all be reduced accordingly (it is monotonic in that sense). Since S must have sum at least k*C, if we ignore S and instead order an equal number of boxes using "The Algorithm", their sum will be at least k*C as well. This proves that "The Algorithm" is the best we can do.
Implementation
"The Algorithm" is really, really simple to code. In fact, this is a complete implementation of a Candy Store solution:
long long T, k, C, prob = 1;
for (cin >> T; T--;) {
cin >> k >> C;
long long sum = 0, num_boxes = 0;
while (sum < k*C) {
num_boxes++;
sum += (sum / k) + 1;
}
cout << "Case #" << prob++ << ": " << num_boxes << endl;
}
Other Cool Stuff
The observant among you may have noticed that this solution is very general, and remains unchanged even if we vary the problem a little. For instance:
- The bound C is effectively useless. We can throw it out and let customers order any amount, as long as the TOTAL order is no more than k*C.
- We can do no better even if we're told all the customers' orders in advance (at the beginning of the day). The "online" solution is just as good as an "offline" one.
- We can do no better even if we constrain the customers to all order the same amount as each other. This was actually the original proposed form of the problem.
Analysis — D. Travel Plan
As with City Tour, this problem is closely related to Hamiltonian cycles. The good news is that here, the graph consists only of points on a line, and is therefore much easier to analyze. The bad news is we aren't looking for just any Hamiltonian cycle, or even the shortest one; we are looking for one of a particular length. A question this precise requires a complete search of some kind.
The simplest approach is to try all possible travel plans one at a time. This is much too slow for the large input, but it is fine for the small input.
Given that N ≤ 30 throughout, you might next think to try a dynamic programming solution that tracks how far you have gone and which nodes you have visited so far. Unfortunately, this is also too slow - large values of F are a big problem!
A 3N solution
The first key step to solving this problem is to go from N! time to 3N time.
We first divide the line into intervals I1, I2, ..., IN-1. Let tj denote the number of times that the travel plan crosses interval Ij, and let dj denote the length of interval Ij. Then the total length of the travel plan is exactly t1 * d1 + t2 * d2 + ... + tN-1 * dN-1. So this means that all we need to do is figure out what each tj should be.
The big question is what tj values are possible? Well, let's take a look.
- Each
tjmust be positive.
Reason: Iftj = 0, then the travel plan never crosses the corresponding interval, and therefore cannot visit every planet. - For each
j,tj - tj-1must be -2, 0, or 2.
Reason: LetPdenote the planet between the intervalsIj-1andIj. In our travel plan, we can stop atPat most once. Every other time, we must travel through, which contributes 1 to bothtj-1andtj. The one time we do hit the planet, we come in along one interval, and then leave along one interval. (These two intervals may or may not be the same.) This part of the travel plan contributes either (a) 1 to bothtj-1andtj, or (b) 2 to one of these values, and 0 to the other. Regardless,tj - tj-1must be -2, 0, or 2. -
t0andtN-1must both be 2.
Reason: Consider the "outside interval"I-1that is past the furthest planets. The travel plan cannot traverse this interval, sot-1 = 0. The observation here now follows immediately from the previous two. - Every choice of
tjsatisfying the previous conditions can be achieved by a legal travel plan.
Reason: We can construct such a travel plan by scanning from left to right across the intervals. At any given time during the construction, we will have decided what the travel plan does to the left of some planetP. Specifically, for each trip left ofP, we will know what the trip does until it goes right ofPagain. We will not however know what happens between these visits, or even what order they occur in.
Now, suppose we want to extend our partial travel plan past the next intervalIj. Iftj = tj-1 - 2, then we need to merge two of our current trips via a stop toP, and extend the rest alongIj. Iftj = tj-1 + 2, then we add a new trip that goes alongIj, stops atP, and then goes back again. In the final case we just extend each trip alongIj, having one stop atPwithout changing direction.
If you think about this for a while, you should be able to convince yourself that this method does indeed generate a valid travel plan.
Okay! We can now describe a 3N time solution to the original problem. Given tj-1, there are at most 3 possible choices for tj. Trying each one in turn, we can iterate over all possible assignments for the tj's, and then pick the one that leads to the optimal length travel plan.
A 3N/2 solution
Even this 3N time algorithm is too slow however. Fortunately, there is a very handy trick for situations like this.
Let's consider the middle interval IN/2 and some fixed value for tN/2. Using the approach described above, we can enumerate in 3N/2 time all choices for t1, t2, ..., tN/2-1 that are consistent with tN/2. Let A be the set of all possible values t1 * d1 + t2 * d2 + ... + tN/2 * dN/2 that can be achieved in this way.
Similarly, we can calculate B, the set of all possible values of tN/2+1 * dN/2+1 + tN/2+2 * dN/2+2 + ... + tN-1 * dN-1 that are consistent with tN/2. All this takes 3N/2 time. What's left is to find two numbers in A and B whose sum is as close as possible to F without exceeding it. One efficient way to do this is to sort B, and then for each element in A, use binary search to decide which element in B you should try matching it with. That gives a O(3N/2 * N) solution.
This can be improved to O(3N/2) by rearranging the formula a little: t1 * (d1 + ... + dN/2) + (t2 - t1) * (d2 + ... + dN/2) + ... + (tN/2 - tN/2-1) * dN/2. The list of these sums can be generated in sorted order iteratively by repeated merging while adding new terms. The difference tj+1 - tj is always one of -2, 0, 2, so we need to merge 3 sorted lists to add a new term.
When we have the two lists A and B in sorted order, we can process them in linear time with a single scan using two pointers.
Analysis — E. Ninjutsu
Getting something discrete
A fact that jumps out immediately is that this problem is not discrete. The rope length that gives an optimal solution might be a real number, and there does not seem to be a way to ensure that this number is rational or discrete in any other way.
Given any real-valued rope length, we can simulate and count the bends, but this number is not a convex function of the rope length, so ternary search is out.
What we really wish we could do is dynamic programming, where the state is a triple -- the point we are currently swinging around, the direction the end of the rope is pointing in, and the length of the rope. Two of these values are real numbers. However, let's see how many different real values we actually need to care about.
As we are swinging the end of the rope around some point P, nothing interesting happens until the moving segment of the rope touches another point, Q. At that... point, we need to make a decision -- we could either bend the rope and switch to swinging around point Q, or cut the rope at exactly point Q and continue swinging around P. There are at most N2 pairs of points, so we only need to consider at most N2 different directions. That takes care of the second DP parameter.
What about the rope length? Using the same reasoning as above, we can show that there is only a finite number of rope lengths that are interesting. Firstly, note that bending the rope does not change its length. Whenever we swing around point P and hit point Q, there is a binary decision -- is the rotating rope segment longer than the distance from P to Q, or shorter?
In other words, the interval of real numbers between 0 and R can be split into a finite number of of sub-intervals, such that the number-of-bends function has a constant value on each sub-interval. This observation suggests the following, naive dynamic programming (DP) solution. The DP state is a pair of points (P, Q) and a real-valued rope length, r. The answer is the maximum number of bends we can achieve by continuing to spin around point P, if we are currently poining in the direction of point Q and have a swinging segment of the rope of length r. To be a bit more precise, we will actually need to have twice as many states -- one for poining in the direction of Q, and one for poining 180 degrees away from Q. We need the second kind of state for the situation when we decide to bend the rope and continue swinging around Q. At that point, we will start pointing in the direction 180 degrees away from Q. One way to implement this solution is simply to use a point, a 2D vector and a length as the state, instead of two points and a length.
Next, let's get rid of the real-valued length as a DP parameter. Because
rope length only changes when we decide to cut it, we can replace the
real-valued length parameter with an integer -- the number of bends since the
last time we have cut the rope. Let's also replace the first two parameters
with the pair of points that caused the cut. We are now interested in all
situations of the following sort -- we were swinging around point P,
with the end of the rope poining in the direction
Floating point issues
We now have an almost completely discrete problem. The only place where floating point numbers are necessary is in the testing of whether the current rope length is long enough to hit some given point, or does the rope's end pass underneath that point? Given the guarantee that the optimal solution works for a long range of rope lengths (0.999999), we can avoid floating point rounding trouble by being conservative: only assume that the rope can hit a point if its length is longer by at least, say, 0.5 than the distance to the point. If it is shorter than that, then certainly such a solution doesn't work for a long enough range of rope lengths, so it's not the optimal solution by the guarantee.
Dealing with loops
The naive solution is too slow. Consider, for example, the case where we
have a rope of length 109 and two points:
First, let's reorganize the naive DP solution a bit to make loop detection
easier. We will have a simpler, three-parameter state and use a memoized
recursive function. Each call of the function will correspond to a situation of
the following kind -- we are spinning around a point P, with the end of
the rope pointing in the direction
Inside the function, we will simulate the wrapping of the rope and make
recursive calls in situations when we decide to cut the rope further. If we
simulate the wrapping process naively, we may need to make a huge number of
recursive calls. Instead, imagine that we find ourselves in a situation
where we have just bent the rope around some point A, and we are about
to bend it again around some point B. If this is not the first time we
have seen the pair
Once we detect a loop, we can choose the number of full revolutions we want to make before we cut the rope and enter inside the convex hull of the points we are looping around. Clearly, it never makes sense to cut off more than one whole loop perimeter. We would be throwing away free rope bends. The optimal number of revolutions is, thus, the total remaining rope length, divided by the perimeter of the loop, floored, minus one.
Putting together a complete solution
We now have a DP solution with O(N^3) states and O(N^2) work per state (linear number of recursive calls; linear amount of work to find the next point for each call). We can speed this up by precomputing next points for each state, but this is not necessary. It turns out that the number of reachable states is small enough for this solution to pass.
Remaining difficulty is in dealing with collinear points. Since all coordinates are integers, this should be done exactly, without using floating point computations.
Analysis — F. The Paths of Yin Yang
Plenty and void grow from each other;
hard and easy foster each other;
long and short shadow each other;
elegance and mudanity prosper together;
music and voice complement each other;
back and front stay together;
they last forever.
This version, translated by our colleague Yifan Shi, is certainly closer to the original meaning of the text.
Impressions
One may discover a series of observations in attacking this problem. Some are obvious, while others need some hard work and inspiration. Our algorithm searches all the possible solutions and counts them. Imagine yourself to be a detective facing such an empty rectangular board. Your job is to reveal all the possible solutions, quickly.
For any solution, as the problem stated, almost all the points have degree (number of neighboring squares with the same color as itself) 2; and there are exactly 4 points having degree 1. Let us call the points with degree 1 end points;
Once we have decided all the degrees, we can try to reconstruct the
color of each square by brute force search. Suppose in a general case,
we have colored a square A, and we also colored all but only
one of its neighbor B, then we do not need to try both
black and white for B, it is decided by the color of the
other squares, and the degree of A.
This gives us a much faster way to recover all the solutions than searching
blindly. One can see that if all the colors of the first row are decided,
and we proceed from top down, then in each step we always have a square
(in fact close to M squares) who is in the same situation as
A above. So, once we decided the combination
(color of the first row, the position of the 4 end points),
all we have to do is to check in O(NM) time if a solution arises.
There are 2M ways to color the first row, and
Θ((NM)4) ways to pick the end points.
Both numbers are too big. One may easily see most of the 2M
colorings of the first row will obviously fail to give a solution,
as we will discuss in the next section. After that, we will work on
how to reduce the number of positions for the end points.
A bit of Topology
Rather than looking at the first row, let us consider the outer loop of the board. That is, the positions on the boundary. It is easy to see that they cannot be of the same color -- the outer loop must contain both black and white squares.
We can say much more about the outer loop. It must be exactly one segment of black squares, and the rest is exactly one segment of white squares! The reason can be seen from the picture on the left below. If there are at least two black segments (and hence at least two white segments), there is no way one can connected both the black pieces and white pieces from the inside of the board.

The second picture shows a forbidden configuration for a 2 by 2 square. If we have a chessboard-like situation, there is no way to connect both black squares and white squares.
Position for end points
Suppose A is a white end point, and B is its sole white neighbor, as in the picture below.
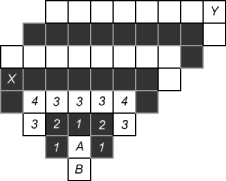
- Because
Ahas no other white neighbors, so the positions labeled with1must be black. - To avoid 2 by 2 chessboard, the positions labeled with
2must be black as well. - Because the first row labeled with 1 and 2 has no other black neighbors, so the positions labeled with
3must be white. - To avoid 2 by 2 chessboard, the positions labeled with
4must be white as well.
X is a point on the boundary, and it is also the place where black and white squares meet on the boundary. Yet we can continue the deduction along the other direction, until we get a point Y on the boundary as well.
This gives a nice connection between the end points and the outer loop. From an end point, we draw two diagonal rays (both with 135 degrees to its neighbor with the same color), both rays hit the boundary either at a corner, or at a point where the black and white squares meet on the outer loop.
Let us summarize our algorithm. We start by fixing the outer loop as a segment of black squares and the rest white. Then from each corner we draw a diagonal line; also from each point on the outer loop that is next to a different color on the loop, we draw one diagonal line going away from the neighbor with the different color. Thus we have 8 diagonals. These diagonals will produce no more than 16 intersections. Those are all the possible positions for the end points.
There are O((N+M)2) ways to fix the outer loop, and thus O((N+M)2) ways to fix the outer loop and the end points. For each of these, one can check if a solution arises in O(MN) time. So the running time is O(MN(N+M)2). The constant is not very small, but tolerable. And one can reduce it using symmetry.
Below is one of a good solution. We may see how the end points and outer loop are connected by the diagonals.
