Google Code Jam Archive — Round 1C 2010 problems
Overview
This last sub-round of round 1 saw the largest number of contestants and the largest amount of controversy. Problem A was about permutations masquerading as a geometry problem. Problem B was a crazy twist on Binary Search. And Problem C was a combination of parsing, dynamic programming and clever trickery.
Load Testing turned out to be the most unusual problem. We received dozens of requests for additional hints and explanations of sample test cases. It was a challenge for the judges to explain the problem as clearly as possible while remaining fair to all contestants. If our responses seemed harsh and unhelpful at times, please know that we tried our best to remain as fair as possible. Perhaps the analysis of Problem B can help clear up any remaining confusion.
ZhukovDmitry finished all 3 problems in just over 38 minutes, closely followed by darnley, who was only 22 seconds behind. aytawgf took the third place in just under one hour of total time.
Congratulations to the 3000 contestants who have advanced to Round 2.
Cast
Problem A. Rope Intranet Written by Cosmin Negruseri. Prepared by Petr Mitrichev.
Problem B. Load Testing Written by Bartholomew Furrow. Prepared by Petr Mitrichev and Bartholomew Furrow.
Problem C. Making Chess Boards Written and prepared by Igor Naverniouk.
Contest analysis presented by Petr Mitrichev, Igor Naverniouk, and Cosmin Negruseri.
Solutions and other problem preparation provided by David Arthur, Xiaomin Chen, Ante Derek, and John Dethridge.
And a special thanks to Martin Gardner, whose books have inspired and educated many of us.
A. Rope Intranet
Problem
A company is located in two very tall buildings. The company intranet connecting the buildings consists of many wires, each connecting a window on the first building to a window on the second building.
You are looking at those buildings from the side, so that one of the buildings is to the left and one is to the right. The windows on the left building are seen as points on its right wall, and the windows on the right building are seen as points on its left wall. Wires are straight segments connecting a window on the left building to a window on the right building.
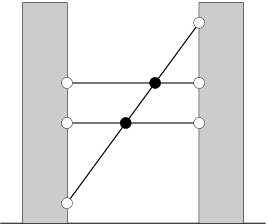
You've noticed that no two wires share an endpoint (in other words, there's at most one wire going out of each window). However, from your viewpoint, some of the wires intersect midway. You've also noticed that exactly two wires meet at each intersection point.
On the above picture, the intersection points are the black circles, while the windows are the white circles.
How many intersection points do you see?
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each case begins with a line containing an integer N, denoting the number of wires you see.
The next N lines each describe one wire with two integers Ai and Bi. These describe the windows that this wire connects: Ai is the height of the window on the left building, and Bi is the height of the window on the right building.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is the number of intersection points you see.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 15.
1 ≤ Ai ≤ 104.
1 ≤ Bi ≤ 104.
Within each test case, all Ai are different.
Within each test case, all Bi are different.
No three wires intersect at the same point.
Small dataset (Test set 1 - Visible)
1 ≤ N ≤ 2.
Large dataset (Test set 2 - Hidden)
1 ≤ N ≤ 1000.
Sample
2 3 1 10 5 5 7 7 2 1 1 2 2
Case #1: 2 Case #2: 0
B. Load Testing
Problem
Now that you have won Code Jam and been hired by Google as a software engineer, you have been assigned to work on their wildly popular programming contest website.
Google is expecting a lot of participants (P) in Code Jam next year, and they want to make sure that the site can support that many people at the same time. During Code Jam 2010 you learned that the site could support at least L people at a time without any errors, but you also know that the site can't yet support P people.
To determine how many more machines you'll need, you want to know within a factor of C how many people the site can support. This means that there is an integer a such that you know the site can support a people, but you know the site can't support a * C people.
You can run a series of load tests, each of which will determine whether the site can support at least X people for some integer value of X that you choose. If you pick an optimal strategy, choosing what tests to run based on the results of previous tests, how many load tests do you need in the worst case?
Input
The first line of the input gives the number of test cases, T. T lines follow, each of which contains space-separated integers L, P and C in that order.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is the number of load tests you need to run in the worst case before knowing within a factor of C how many people the site can support.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 1000.
2 ≤ C ≤ 10.
L, P and C are all integers.
Small dataset (Test set 1 - Visible)
1 ≤ L < P ≤ 103.
Large dataset (Test set 2 - Hidden)
1 ≤ L < P ≤ 109.
Sample
4 50 700 2 19 57 3 1 1000 2 24 97 2
Case #1: 2 Case #2: 0 Case #3: 4 Case #4: 2
Explanation
In Case #2, we already know that the site can support between 19 and 57 people. Since those are a factor of 3 apart, we don't need to do any testing.
In Case #4, we can test 48; but if the site can support 48 people, we need more testing, because 48*2 < 97. We could test 49; but if the site can't support 49 people, we need more testing, because 24 * 2 < 49. So we need two tests.
C. Making Chess Boards
Problem
The chess board industry has fallen on hard times and needs your help. It is a little-known fact that chess boards are made from the bark of the extremely rare Croatian Chess Board tree, (Biggus Mobydiccus). The bark of that tree is stripped and unwrapped into a huge rectangular sheet of chess board material. The rectangle is a grid of black and white squares.
Your task is to make as many large square chess boards as possible. A chess board is a piece of the bark that is a square, with sides parallel to the sides of the bark rectangle, with cells colored in the pattern of a chess board (no two cells of the same color can share an edge).
Each time you cut out a chess board, you must choose the largest possible chess board left in the sheet. If there are several such boards, pick the topmost one. If there is still a tie, pick the leftmost one. Continue cutting out chess boards until there is no bark left. You may need to go as far as cutting out 1-by-1 mini chess boards.
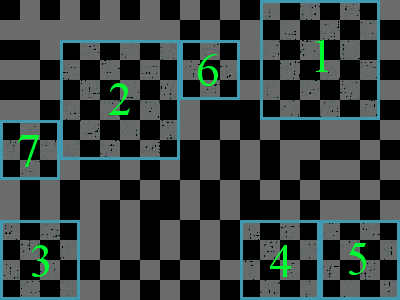
Here is an example showing the bark of a Chess Board tree and the first few chess boards that will be cut out of it.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each one starts with a line containing the dimensions of the bark grid, M and N. N will always be a multiple of 4. The next M lines will each contain an (N/4)-character hexadecimal integer, representing a row of the bark grid. The binary representation of these integers will give you a strings of N bits, one for each row. Zeros represent black squares; ones represent white squares of the grid. The rows are given in the input from top to bottom. In each row, the most-significant bit of the hexadecimal integer corresponds to the leftmost cell in that row.
Output
For each test case, output one line containing "Case #x: K", where x is the case number (starting from 1) and K is the number of different chess board sizes that you can cut out by following the procedure described above. The next K lines should contain two integers each -- the size of the chess board (from largest to smallest) and the number of chess boards of that size that you can cut out.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 100;
N will be divisible by 4;
Each hexadecimal integer will contain exactly N/4 characters.
Only the characters 0-9 and A-F will be used.
Small dataset (Test set 1 - Visible)
1 ≤ M ≤ 32;
1 ≤ N ≤ 32.
Large dataset (Test set 2 - Hidden)
1 ≤ M ≤ 512;
1 ≤ N ≤ 512;
The input file will be at most 200kB in size.
Sample
4 15 20 55555 FFAAA 2AAD5 D552A 2AAD5 D542A 4AD4D B52B2 52AAD AD552 AA52D AAAAA 5AA55 A55AA 5AA55 4 4 0 0 0 0 4 4 3 3 C C 4 4 6 9 9 6
Case #1: 5 6 2 4 3 3 7 2 15 1 57 Case #2: 1 1 16 Case #3: 2 2 1 1 12 Case #4: 1 2 4
The first example test case represents the image above.
Analysis — A. Rope Intranet
This problem was easier than it could have been, since the constraints don't require you to write an efficient solution. To solve it you can simply iterate through each pair of ropes and test if they intersect. Checking for intersection can be done in various ways. One way is to write the two line equations and then solve a system of linear equations with two variables to find the intersection point. An easier solution is to simply check if the order of the ends of the pair of ropes on the first building is the opposite of the order of the ends of the ropes on the second building. This translates to the code:
(A[i] - A[j]) * (B[i] - B[j]) < 0This algorithm takes O(n2) and it's fast enough to solve our problem.
This problem is very similar to the classic one which asks for the number of inversions within a given permutation. An inversion for a permutation p is a pair of two indexes i < j such that pi > pj. Let's see why these problems are equivalent. If ra is the rank of A[i] when we sort A and rb is the rank of B[i] when we sort B, then the ropes problem becomes the inversion count problem on the permutation p where pra = rb for each i.
This new problem is a good application for divide and conquer algorithms, and can be solved in O(n log n) time. Merge sort can be adapted nicely to not only sort an array, but count the number of inversions as well. Other solutions use data structures like segment trees, augmented balanced binary search trees or augmented skip lists.
Number of inversions in a permutationAnalysis — B. Load Testing
Understanding the sample cases
In order to solve this problem, one first needs to get a feeling of what's asked, and looking at the sample cases is a good way to achieve that.
Take a look at the first sample case. The answer given is 2. How do we achieve the result with just 2 loadtests? Let's make a couple guesses. Suppose we do a loadtest that checks if the site supports 100 users. If we learn that the site can't support 100 users, then we're done: we know we can support 50 users but can't support 100 which is 50*2. However, if we learn that the site can actually support 100 users, we have a very difficult task at hand now: we have only one loadtest left, and we know that the site can support 100 users but can't support 700. Is it possible to solve it?
Suppose we now loadtest to check if the site supports 300 users. If we learn that the site can't support 300 users, then we've failed to solve the problem: we know we can support 100, but can't support 300 - but 300 is more than 100*2, so we don't have enough knowledge. Moreover, this actually helps us to prove that our loadtest must test for 200 users or less, otherwise we will hit the same issue.
Now we know that our second loadtest must use at most 200 users. But even when it's exactly 200, suppose we learn that our site can actually support all of them. Then we've failed to solve the problem again: we know we can support 200, but can't support 700 - but 700 is more than 200*2.
So there's no good choice for our second loadtest. It means that the choice of the first loadtest was wrong - 100 users is too small for it.
What have we learned?
However, we've learned an important lesson in our failed attempt to understand the example case: when we have only one loadtest left, and we know that the site can support L people but can't support P people, we must loadtest with such number X that L*C>=X, and at the same time X*C>=P. The first inequality will help us solve the problem when the loadtest fails, and the second one is helpful if the loadtest succeeds.
Since there's no such number X for L=100, P=700, C=2, our first attempt above has failed.
The question now is: how to check if such X exists? From the first equation, we get X<=L*C. From the second one, we get X>=P/C. Such X exists if and only if L*C>=P/C, which means L*C2>=P. Forgetting the formulas, the upper bound of our range should be at most C2 times more than the lower bound. In that case, we can just take X=L*C for our only loadtest.
The second attempt at understanding the first sample case
Equipped with this knowledge, we get back to the first sample case. 100 was wrong since 100*22=100*4<700. Maybe we should loadtest for 300 people first? If the loadtest succeeds, then we will have one loadtest left, 300 people OK, 700 people not OK, and since 300*4>=700, we can solve the problem. However, what if the loadtest doesn't succeed? We know that our system can support 50 people but can't support 300 people and have only one loadtest left. Since 50*4<300, we can't do that. So the choice of 300 was also wrong.
What if we try 200 as the first loadtest? In case it succeeds, we get one loadtest, 200 OK, 700 not OK, 200*4>=700 - we can do that. In case it fails, we get 50 OK, 200 not OK, 50*4>=200 - we can do that as well. So we've finally figured out the algorithm to solve the first sample case using just 2 loadtests:
Loadtest for 200 people. If the site can support 200 people: Loadtest for 400 people. If the site can't support 200 people: Loadtest for 100 people.
What have we learned?
So how do we figure out if two loadtests are enough? This is actually surprisingly similar to the study of the one loadtest case.
When we have two loadtests left, and we know that the site can support L people but can't support P people, we must loadtest with such number X that L*C2>=X, and at the same time X*C2>=P. The first inequality will help us solve the problem using one remaining loadtest when the loadtest fails, and the second one is helpful if the loadtest succeeds.
Using the same argument as above, one can see that such number X exists if and only if L*C4>=P (we got C4 as C2*C2).
More loadtests?
Now it's not so hard to figure out what happens with more than two loadtests. It's possible to solve the problem using three loadtests if and only if L*C8>=P. For four loadtests, we get L*C16>=P. And so on. That pretty much describes the solution for this problem.
Understanding the sample cases, attempt 3
Now we can finally figure out the algorithm to solve the third sample case: L=1, P=1000, C=2. In order to do this in four loadtests, our first loadtest can be for L*C8=256:
Loadtest for 256 people. If the site can support them:
Loadtest for 512 people.
If we can't support 256 people:
Loadtest for 16 people. If the site can support them:
Loadtest for 64 people. If the site can support them:
Loadtest for 128 people.
If we can't support 64 people:
Loadtest for 32 people.
If we can't support 16 people:
Loadtest for 4 people. If the site can support them:
Loadtest for 8 people.
If we can't support 4 people:
Loadtest for 2 people.
This looks quite similar to the binary search algorithm, but performed on exponential scale.
Conclusion
We started solving this problem by trying to understand the answers for the sample cases, and by the time we actually understood them, we already have a complete solution. The only remaining thing is to implement the solution carefully avoiding the integer overflow issues.
Analysis — C. Making Chess Boards
Finding the largest chess board
First, we need a quick way to find the largest chess board. There is classic dynamic programming trick that goes like this. Let's compute, for each cell
if (board[i - 1][j] != board[i][j] &&
board[i][j - 1] != board[i][j] &&
board[i - 1][j - 1] == board[i][j]) {
larg[i][j] = 1 + min(larg[i - 1][j],
larg[i][j - 1],
larg[i - 1][j - 1]);
}
In a single, linear-time, row-by-row scan, we can compute the values of larg[][] for all cells.
Finding the chess board to remove
Now that we have larg[][], it is very easy to find the first chess board that we should cut out. Its bottom-right corner is in the cell that has the largest possible value in larg[][]. If there are several such cells, we use the tie-breaking rules described in the problem and choose the one that comes first in lexicographic order of
We can do this in linear time by scanning larg[][], but since we will have to do this many times, it is better to make a heap of triples of the form
(-larg[i][j], i, j)and take the smallest element from that heap. This way, we are sorting all cells by decreasing size, then by increasing row, then by increasing column. As long as we can update this heap efficiently after cutting out a chess board, we can always retrieve the smallest element in
Removing the chess board and updating larg[][]
Consider removing the first 6x6 chess board from the example input described in the problem statement. How should we update larg[][]? First of all, we can fill the 6x6 square of cells with zeros because there are no more chess boards to be removed from those locations. But that is not all. There are other cells that might need to be updated. Where are they, and how many of them are there?
Naively, we can simply recompute the values of all non-zero cells in larg[][] and continue. If we do that, we will have a
First of all, notice that we do not need to update rows above or to the left of the 6x6 square. Any square chess boards whose bottom-right corners are in those areas still exist and can be cut out later. The only chess boards that we need to worry about are those that overlap the 6x6 board that we have just removed. Also, notice that we have just removed the largest possible chess board, so we only need to care about remaining boards of size 6 or smaller. Where can their bottom-right corners lie in order for those boards to overlap our board? They must be in the 12x12 square whose center is at
That's an area of size
Updating the heap
Each time we update larg[][], we must also update the heap that lets us find the next board to remove. This means finding and removing an old entry, as well as inserting a new entry. With pointers from cells to heap elements, or by using a balanced binary search tree, both steps can be done in
In total, this algorithm runs in