Google Code Jam Archive — Round 3 2009 problems
Overview
This round featured some of the toughest problems we could come up with. Of the four we posed, only one was a somewhat "standard" problem in any sense; the others all required ingenuity or insight of some sort. All the problems were solved, though only barely; KOTEHOK, the only contestant to solve D-large, didn't have time to solve enough other problems to make it into the top 25.
For the judges, this was by far the most fun round to watch. bmerry, a familiar figure at the top of the scoreboard, took the lead with half an hour to go, and held onto it. ACRush, who won last year's competition and finished Round 2 with more than half the time to spare, got off to a slow start: he was briefly out of the top 25 before roaring into 5th place 2 hours in and holding on to claim his spot in the final. And, of course, we love to see all of the different colours on the scoreboard: if they can all make it, this year's finalists will represent 15 different countries.
Congratulations to everyone who made it this far, and special congratulations to the top 25, who win a trip to Mountain View, California and a chance to compete in the Google Code Jam 2009 World Finals!
Cast
Problem A. EZ-Sokoban Written by Mohamed Eldawy. Prepared by Tomek Czajka and Marius Andrei.
Problem B. Alphabetomials Written and prepared by Xiaomin Chen.
Problem C. Football Team Written by John Dethridge. Prepared by Ante Derek, Xiaomin Chen and John Dethridge.
Problem D. Interesting Ranges Written by Petr Mitrichev. Prepared by Pablo Dal Lago and Bartholomew Furrow.
Contest analysis presented by Xiaomin Chen, Tomek Czajka, Bartholomew Furrow, and Petr Mitrichev.
Solutions and other problem preparation provided by Petr Mitrichev and Igor Naverniouk.
A. EZ-Sokoban
Problem
Sokoban is a famous Japanese puzzle game. Sokoban is Japanese for "warehouse keeper". In this game, your goal is to push boxes to their designated locations in the warehouse. To push a box, the area behind the box and in front of the box must be empty. This is because you stand behind the box when pushing and you can push only one box at a time. You cannot push a box out of the board and you cannot stand outside the board when pushing a box.For example, in this picture:

Sokoban was proved to be a P-Space complete problem, but we deal with an easier variation here. In our variation of Sokoban, boxes have strong magnets inside and they have to stick together almost all the time. Under "stable" conditions, all boxes should be connected, edge to edge. This means that from any box we can get to any other box by going through boxes that share an edge. If you push a box and boxes are no longer connected, you are in "dangerous mode". In dangerous mode, the next push must make the boxes connected again.
For example, in this picture:



A Sokoban puzzle consists of a board, initial configuration of the boxes and the final configuration (where we want the boxes to be at the end). Given an EZ-Sokoban puzzle, find a solution that makes the minimum number of box moves, or decide that it can't be solved. The final and initial configurations will not be in "dangerous" mode.
To simplify things, we will assume that you, the warehouse keeper, can jump at any time to any empty spot on the board.
Input
The first line in the input file contains the number of cases, T.Each case consists of several lines. The first line contains R and C, the number of rows and columns of the board, separated by one space. This is followed by R lines. Each line contains C characters describing the board:
- '.' is an empty spot
- '#' is a wall
- 'x' is a goal (where a box should be at the end)
- 'o' is a box
- 'w' is a both a box and a goal
Output
For each test case, output
Case #X: Kwhere X is the test case number, starting from 1, and K is the minimum number of box moves that are needed to solve the puzzle or -1 if it cannot be solved.
Limits
Memory limit: 1 GB.
1 ≤ R,C ≤ 12
Small dataset
Time limit: 30 seconds.
1 ≤ the number of boxes ≤ 2
Large dataset
Time limit: 45 seconds.
1 ≤ the number of boxes ≤ 5
Sample
4 5 4 .... #..# #xx# #oo# #..# 7 7 .###### .x....# .x....# ..#oo.# ..#...# .###### .###### 4 10 ########## #.x...o..# #.x...o..# ########## 3 4 .#x. .ow. ....
Case #1: 2 Case #2: 8 Case #3: 8 Case #4: 2
B. Alphabetomials
Problem
As we all know, there is a big difference between polynomials of degree 4 and those of degree 5. The question of the non-existence of a closed formula for the roots of general degree 5 polynomials produced the famous Galois theory, which, as far as the author sees, bears no relation to our problem here.
We consider only the multi-variable polynomials of degree up to 4, over 26 variables, represented by the set of 26 lowercase English letters. Here is one such polynomial:
aber+aab+c
Given a string s, we evaluate the polynomial on it. The evaluation gives p(S) as follows: Each variable is substituted with the number of appearances of that letter in S.
For example, take the polynomial above, and let S = "abracadabra edgar". There are six a's, two b's, one c, one e, and three r's. So
p(S) = 6 * 2 * 1 * 3 + 6 * 6 * 2 + 1 = 109.
Given a dictionary of distinct words that consist of only lower case letters, we call a string S a d-phrase if
S = "S1 S2 S3 ... Sd",where Si is any word in the dictionary, for 1 ≤ i ≤ d. i.e., S is in the form of d dictionary words separated with spaces. Given a number K ≤ 10, your task is, for each 1≤ d ≤ K, to compute the sum of p(S) over all the d-phrases. Since the answers might be big, you are asked to compute the remainder when the answer is divided by 10009.
Input
The first line contains the number of cases T. T test cases follow. The format of each test case is:
A line containing an expression p for the multi-variable polynomial, as described below in this section, then a space, then follows an integer K.
A line with an integer n, the number of words in the dictionary.
Then n lines, each with a word, consists of only lower case letters. No word will be repeated in the same test case.
We always write a polynomial in the form of a sum of terms; each term is a product of variables. We write at simply as t a's concatenated together. For example, a2b is written as aab. Variables in each term are always lexicographically non-decreasing.
Output
For each test case, output a single line in the form
Case #X: sum1 sum2 ... sumKwhere X is the case number starting from 1, and sumi is the sum of p(S), where S ranges over all i-phrases, modulo 10009.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 100.
The string p consists of one or more terms joined by '+'. It will not start nor end with a '+'. There will be at most 5 terms for each p. Each term consists at least 1 and at most 4 lower case letters, sorted in non-decreasing order. No two terms in the same polynomial will be the same.
Each word is non-empty, consists only of lower case English letters, and will not be longer than 50 characters. No word will be repeated in the same dictionary.
Small dataset
Time limit: 30 seconds.
1 ≤ n ≤ 20
1 ≤ K ≤ 5
Large dataset
Time limit: 60 seconds.
1 ≤ n ≤ 100
1 ≤ K ≤ 10
Sample
2 ehw+hwww 5 6 where when what whether who whose a+e+i+o+u 3 4 apple orange watermelon banana
Case #1: 15 1032 7522 6864 253 Case #2: 12 96 576
C. Football Team
Problem
A football team will be standing in rows to have a photograph taken. The location of each player will be given by two integers x and y, where y gives the number of the row, and x gives the distance of the player from the left edge of the row. The x values will be all different.
In order to make the photo more interesting, you're going to make sure players who are near each other have shirts of different colors. To do this, you set the following rule:
For each player P:
- The closest player to the right of P in the same row, if there is such a player, must have a different shirt color.
- The closest player to the right of P in the previous row, if there is such a player, must have a different shirt color.
- The closest player to the right of P in the next row, if there is such a player, must have a different shirt color.
More formally, if there is a player at (x1,y1) and (x2,y2), where x1<x2, then those two players must have different shirt colors if:
- y1 - 1 ≤ y2 ≤ y1 + 1, and
- there is no x3 such that there is a player at (x3, y2) and x1 < x3 < x2.
Find the minimum number of distinct shirt colors required so that this is possible.
Input
The first line of input contains a single integer T, the number of test cases. Each test case starts with a line that contains an integer N, the number of players, followed by N lines of the form
x yeach specifying the position of one player.
Output
For each test case, output
Case #X: cwhere X is the test case number, starting from 1, and c is the minimum number of colors required.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1 GB.
1 ≤ T ≤ 100
1 ≤ x ≤ 1000
The values of x will all be different.
Small dataset
1 ≤ y ≤ 15
1 ≤ N ≤ 100
Large dataset
1 ≤ y ≤ 30
1 ≤ N ≤ 1000
Sample
3 3 10 10 8 15 12 7 5 1 1 2 1 3 1 4 1 5 1 3 1 1 2 2 3 1
Case #1: 1 Case #2: 2 Case #3: 3
D. Interesting Ranges
Problem
A positive integer is a palindrome if its decimal representation (without leading zeros) is a palindromic string (a string that reads the same forwards and backwards). For example, the numbers 5, 77, 363, 4884, 11111, 12121 and 349943 are palindromes.
A range of integers is interesting if it contains an even number of palindromes. The range [L, R], with L ≤ R, is defined as the sequence of integers from L to R (inclusive): (L, L+1, L+2, ..., R-1, R). L and R are the range's first and last numbers.
The range [L1,R1] is a subrange of [L,R] if L ≤ L1 ≤ R1 ≤ R. Your job is to determine how many interesting subranges of [L,R] there are.
Input
The first line of input gives the number of test cases, T. T test cases follow. Each test case is a single line containing two positive integers, L and R (in that order), separated by a space.
Output
For each test case, output one line. That line should contain "Case #x: y", where x is the case number starting with 1, and y is the number of interesting subranges of [L,R], modulo 1000000007.
Limits
Time limit: 45 seconds per test set.
Memory limit: 1 GB.
Small dataset
1 ≤ L ≤ R ≤ 1013Large dataset
1 ≤ L ≤ R ≤ 10100Sample
3 1 2 1 7 12 110
Case #1: 1 Case #2: 12 Case #3: 2466
Analysis — A. EZ-Sokoban
This is a state space search problem: given a set of states (positions on the board), an initial state and a final state, and rules for state transformations, find a sequence of moves that transforms the initial state to the final state. In our case, the problem asks for the length of the shortest such sequence of moves.
Conceptually, we can represent such a state space as a graph. The nodes of the graph are the possible positions, and the edges are the allowed moves. The problem then becomes: find the shortest path in the graph. The standard algorithm to solve this graph problem is breadth-first search.
Let's estimate the number of nodes in the graph. Assuming the maximum number of boxes (5), first estimate the number of positions where all the boxes are connected. 5 connected boxes form a pentomino. There are 63 different pentominoes, counting all rotations and reflections. Each of these can be positioned at no more than 12*12 different positions. Hence we get an upper bound of 63*12*12 = 9072 connected positions. It is a little more difficult to estimate the "dangerous" positions accurately, but we can see that from each connected position there are not too many moves, so we can guess that the total is not going to be too large for our computer to handle.
One approach would be to first generate the graph with all the edges explicitly, and then run the breadth-first-search on it. Another is to not store the graph at all, but compute the possible moves (edges) from a given position as we go, and only store the set of visited positions in a data structure.
Some details to work out are:
- How to represent positions. A simple list of box coordinates can work. One can also use a whole-board bit-mask.
- How to look up positions. We need this to see if a position has already been visited, or to avoid constructing the same node in the graph multiple times. We can use some kind of a dictionary data structure - a hash table or a binary search tree.
- How to generate moves. Just try moving all the boxes in every direction, if the space in front and in the back of the box is empty. We also have to make sure that we don't move from a dangerous position to another dangerous position.
- How to check whether a position is dangerous. To do this, we need to check if our 1 to 5 boxes are all connected. This can be represented as another, small graph problem (graph connectivity). We run another breadth-first-search on the little graph, where the nodes are the boxes and the edges indicate whether two boxes touch. Another approach would be to pre-generate all polyominoes of sizes up to 5, store them in a hash table, and then look up the shape appearing in a given position.
Analysis — B. Alphabetomials
1. Product of two sets
The problem was created during a short walk in Manhattan in a summer evening. At first there came the picture of an N by M matrix. Let A be a set of N words {Ai | 1 ≤ i ≤ N}, and B be a set of M words {Bj | 1 ≤ j ≤ M}. For any word X, let us denote X(c) the number of occurrences of character c in X. In the (i,j)-entry of the matrix, we write, say, the product Ai('a')Bj('a')Bj('b'). What is the sum of all the entries in the matrix?
One can compute the NM terms one by one. But it is easy to see, as you can sum them row by row, as well as column by column, it is nothing but the full expansion of the following expression
(1) ∑X ∈ A, Y ∈ BX('a')Y('a')Y('b') = ∑X ∈ AX('a') ∑Y ∈ BY('a')Y('b').i.e., you can compute the sum on A and B separately, then compute their product.
What if, as in our problem, instead of writing Ai('a')Bj('a')Bj('b') for the (i,j)-entry, we write Z('a')2Z('b'), where Z is the concatenation of Ai and Bj? i.e., we do not care which 'a's are from the first set, and which are from the second. In this case we do not have something as simple as (1). But, we can reduce it if we do care which of the 'a's are from the first set. We use a somehow simplified notation (which is closer to our problem statement) -- the symbol a now also represent the number of 'a's in a string. For a fixed string Z that is a concatenation of words from A and B, let a1 denote the number of 'a's contributed by the first set, and a2 the number of 'a's contributed by the second set. For each entry in the matrix, we write a2b, this is equal to (a1+a2)2(b1+b2). Expand it, we have
(2) ∑X ∈ A, Y ∈ B a2b = ∑X ∈ A, Y ∈ B (a1+a2)2(b1+b2)In the last step, for each summand, since the characters from the first set and those from the second set are nicely separated, we can apply the same reason for (1).
= ∑X ∈ A, Y ∈ B (a12b1 + a12b2 + 2a1a2b1 + 2a1a2b2 + a22b1 + a22b2)
= ∑A,B (a12b1) + ∑A,B (a12b2) + 2∑A,B (a1a2b1) +
2∑A,B (a1a2b2) + ∑A,B (a22b1) + ∑A,B (a22b2)
= ∑A a2b ∑B 1 + ∑A a2 ∑B b + 2∑A ab ∑B a +
2∑A a ∑B ab + ∑A b ∑B a2 + ∑A 1 ∑B a2b
2. Product of ten sets
Our problem asks to compute the sum of expressions such like a2b over the product of a dictionary set by itself up to 10 times. (Or more generally, we can think of the product of 10 sets.) The size of the product set is the huge number n10. But if we use the same trick as in the previous section, write a2b as(a1 + a2 + ... + a10)2 (b1 + b2 + ... + b10)and expand it. Then we reduce the problem to at most KD easier problems, where D is the maximal degree (K ≤ 10 and D ≤ 4 in our problem). Each of the easier problems can be solved similar as in (1).
This gives one solution to our problem. Focus on one monomial a time. We are basically choosing the origin (one of the ten sets) for each letter in the monomial, so each set gets a sub-monomial, which can be expressed as a subset of the indices of the letters in the original monomial.
We pre-compute ∑X ∈ Aq(X) for each sub-monomial q, there are at most 16 of these. Then for each of the KD "easier problems", the computation involves only multiplying K of the pre-computed numbers.
3. Speedups
The solution above can be easily sped up to solve for much bigger K and slightly bigger D, if one compute the summations incrementally, do the product of two sets in each step (you call it dynamic programming or not).
First, we compute the sum for A × A, not only for the monomial, but for all its sub-monomials. Then we compute the sums over A3. Now we can view A3 as A2 × A. Each sub-monomial can be expanded to at most 2D terms, and every one of them submit to the simple trick in (1). Because we already have the summation of A2 on any sub-monomial, each of the 2D problems can be solved in constant time. The running time of this solution is mostly dominated by O(3DK) for each monomial form the input.
Observe the last line in (2), notice that we only have one dictionary set in our problems, so we can ignore the subscripts -- A, B, etc are the same set. There are other speedups available along this line by exploring the symmetry in indices. We omit the details.
4. The theory behind it
In case you are familiar with discrete probability, you may well know that probability theory provides some powerful abstract machinery for counting. What we went through so far are just some easy exercises in probability. And solving this problem with the abstract theory in mind certainly speeds up your thinking and boosts your confidence in the solution.
Especially, we went through the important fact that the expectation of the product of K random variables equals to the product of the expectation of each of the variables, given that the K random variables are mutually independent. The interested readers may carry the formal correspondences out.
Analysis — C. Football Team
0. Drawing the graph
It is clear from the statement that this is a graph coloring problem -- on 1000 vertices. But certainly this is not the end of the story. There must be something special that makes this famous NP-complete problem solvable in this contest.
Represent each player with a vertex, and draw an edge between two players if they cannot use the same color. Obviously we can just draw the graph with each player in his position (x, y).
So there are at most 30 rows of players. Can this help? Observing this fact leads to solutions that are good enough for the small dataset, but not for the large tests.
On each row, the edges form a horizontal line segment from the leftmost point to the rightmost. All the other edges are between two adjacent rows. And more importantly, it is not hard to observe and prove the following:
- If there are at least two edges between two adjacent rows, then all these edges together with the horizontal row edges form triangles.
- If you draw all the edges using straight line segments, none of the edges cross each other in the middle.
- One color is enough if and only if there are no edges.
- In a general graph, it is well known that the graph is 2-colorable if and only if there are no odd cycles. In our problem, it is even simpler than that. One can prove that whenever there is a cycle, there must also exist a triangle. So, the graph is 2-colorable if and only if it is a tree, as well as if and only if there is no triangles.
So this is a good news: besides the simple special cases, all we need to decide is whether the answer is 3 or 4. Unfortunately it is also known that even this problem is NP-complete in general.
As we mentioned earlier, we are dealing with a special case of even planar graphs. It is mostly triangulated, and nicely positioned in rows with all edges only from adjacent rows. It turns out that there are many solutions to this problem. Let us describe a few in the rest of this writing. In all the solutions, we try to color the graph with just 3 colors A, B,and C, and if this fails, the answer is 4. Also, to simplify our writing, we assume every point has degree at least 3 -- otherwise we can simply remove it without changing the 3-colorability.
1. The colors are pretty much forced
Pick any triangle. Its vertices must be colored with different colors. We color them with A, B,and C. Now, there might be another triangle next to it. i.e., sharing an edge e with it. In that triangle, two vertices of e are already colored; if the third one is not, its color is decided now!
From another point of view, this is simply the following: Whenever there is a vertex with two adjacent neighbors colored, we color it with the third color.
Because every color is forced, the answer is 4 as soon as we see a conflict.
We can do this forced coloring almost all the way. It is easy to see we only need to pause a little when there is a cut point. But this is not hard either: the point separates the graph into an upper part and a lower part, as long as we can color both parts with 3 colors, we can paste them together.
2. The dual graph
There is a deeper concept revealed in the solution above. We were actually considering the dual graph of a planar graph, which itself is also planar. Each face (in our problem, each triangle) in the original graph becomes a point, and two points are connected if the two faces share an edge.
If you are familiar with the algorithm that 2-colors a graph and detects odd cycles, you may find it very similar to our solution above. We are going to argue that our original graph is 3-colorable if and only if the dual graph is 2-colorable (with one color for all the clockwise triangles).
Observe that if the original graph is 3-colorable, and one triangle gets its three vertices colored A, B, C in clockwise order, then any triangle adjacent to it must have its vertices colored A, B, C in counter-clockwise order. Thus, the original graph being 3-colorable implies its dual is 2-colorable.
The proof of the reversed direction is also not hard to envisage, but it involves more details and requires some additional conditions on our graph. One easy way to prove it is with induction on rows.
3. The local property
The solution above does not allow a much simpler implementation. But it leads to an even nicer observation. We call a vertex in the original graph an inner vertex if it is surrounded by triangles in all the directions. The following fact gives the simplest solution to our problem:
The graph is 3-colorable if and only if there is no inner vertex with odd degree.The rest of this section is devoted to the proof of this fact. If you feel that some of the claims about the planar graph and its dual are not obvious, try to draw some and convince yourself.
Any inner vertex v with degree d is surrounded by d triangles sharing the same vertex. In the dual, they give a cycle of length d that enclose v in the middle.
One direction of the proof is easier. If v has odd degree, then we see an odd cycle in the dual, therefore the original graph is not 3-colorable.
Now assume there is any odd cycle, let us pick C -- the one with the smallest enclosing area. We claim that C must enclose only one inner vertex, and therefore we find an inner point with odd degree. This can be proved in several ways with some details. Basically, if there are two inner vertices enclosed, one can find a path that separates them and hit C in two places. This divides the enclosing area of C into two smaller areas, and it is not hard to see one of the areas must be enclosed by an odd cycle. This contradicts the assumption that C is the odd cycle with smallest area, and completes the sketched proof of our short solution.
In the picture below, there is a big cycle with length 9, and v is an inner vertex surrounded by a cycle with length 5.
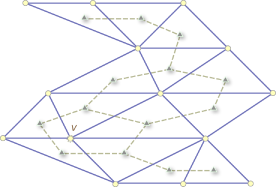
4. Other solutions
We mention two brute-force solutions that are good enough for the small dataset. In order to use them for the large dataset, one needs to optimize a great deal, and possibly just discover one of keys for the polynomial solutions as mentioned above.Again, we look at the original graph. We assume the graph is connected, and every vertex has degree at least 3.
Notice that there are at most 30 rows. One can fix the color of the first vertex in each row. There are 2rows ways of doing this (as opposed to 3rows). Once this is fixed, all the rest of the coloring is determined, for a reason similar to the one explained in Section 1.
Another solution is dynamic programming: do a sweep from the right to the left, and remember the color of the first vertex to the right on each row. Notice that you cannot do this from left to right, since knowing the color of only one vertex on a row is not enough in that direction.
More information
Graph coloring - Four color theorem - Dual graph
The solution with the local property resembles very much a theorem of Heawood from 1898: that a maximal planar graph is 3-colorable if and only if every degree is even. A more general theorem, which implies our solution, can be found in the paper A new 3-color criterion for planar graphs by Krzysztof Diks, Lukasz Kowalik, and Maciej Kurowski.
Analysis — D. Interesting Ranges
1. How big can the answer be?
First, let's get a crude upper bound on the answer. More specifically, if L=1 and R=N, there are N*(N+1)/2 subsegments of [L,R]. Not all of them will contain an even number of palindromes, but a significant part (roughly half) will.
So even for the small input we might get more than 10^25 segments in the answer; it's obvious we can't enumerate them one by one. We have to figure out a way to process them in bulks.
2. First optimization
The first idea required to solve the small dataset helps us reduce the number of segments to consider from O(N^2) to O(N). To achieve that, we rely on the following observation: [L,R] can be represented as [0,R] minus [0,L-1]; thus it contains an even number of palindromes if and only if [0,L-1] and [0,R] both contain even or both contain odd number of palindromes.
But how exactly does that help us? Suppose we know which of [0,X] segments contain even number of palindromes (we'll call them just "even 0-segments" further on) and which contain odd number of palindromes ("odd 0-segments"). We know that each interesting segment corresponds to exactly one pair of even 0-segments or to exactly one pair of odd 0-segments. But this is true the other way around as well: each pair of distinct even 0-segments corresponds to exactly one interesting segment, and so does each pair of distinct odd 0-segments! (when X is between L-1 and R, inclusive).
That means that if there are A even 0-segments and B odd 0-segments, the answer is A*(A-1)/2+B*(B-1)/2.
2. Second optimization
But we can't even afford O(N) running time since N is 10^13 even in the small dataset! So we have to do another optimization.
Let's write out an infinite string of zeroes and ones, with X-th symbol (0-based) being equal to 0 if [0,X] contains an even number of palindromes, and equal to 1 if [0,X] contains an odd number of palindromes. What we need to find in this problem is how many zeroes (number A above) and ones (number B above) are there in the substring starting with (L-1)-th character and ending with R-th character of this string.
This string looks like this: 1010101010011111111111000000000001111111111100...
Now we can spot the second optimization: zeroes and ones tend to go in big blocks in this string. More specifically, one changes to zero or vice versa only when we pass a palindrome. And there are only O(sqrt(N)) palindromes up to N - so the number of groups of consecutive zeros or ones in the first N characters is O(sqrt(N)).
All groups except maybe two boundary ones fit into [L-1,R] segment entirely. So we just need to sum them all and handle the boundary ones carefully, and we get an O(sqrt(N)) algorithm that is sufficient to solve the small dataset.
We can also reduce the number of boundary groups to consider from two to one relying on the fact that the number of zeroes/ones in [L-1,R] is the number of zeroes/ones in [0,R] minus the number of zeroes/ones in [0,L-2].
3. Third optimization
So what about the large one? Sqrt(10^100)=10^50, so we're definitely not there yet.
The final optimization idea still relies on the above infinite string of zeroes and ones. You might have noticed already that many blocks of ones and zeroes have the same length. For example, block of ones from 11 to 21 has length 11, and so is the block of zeroes from 22 to 32, ones from 33 to 43, zeroes from 44 to 54, and so on.
This is because of the fact that a palindrome number is uniquely determined by its first half. For example, consider 6-digit palindrome number 127721. What is the next 6-digit palindrome number? 128821. It's followed by 129921, 130031, and so on. As you can see, in most cases the difference between two consecutive 6-digit palindrome numbers is 1100 (change of +1 in two middle digits). And the difference between two consecutive palindrome numbers is exactly the length of the block of ones/zeroes!
But there are also some blocks which have length different from usual. For example, the block of zeroes from 88 to 98 still has 11 numbers, but the block of ones from 99 to 100 has just two numbers; then follow several blocks of 10 (zeroes from 101 to 110; ones from 111 to 120; ...; zeroes from 181 to 190), then we have a block of 11 ones from 191 to 201.
The above explanation about consecutive palindromes allows us to understand why there are such unusual-length blocks. It happens in two cases: when the amount of digits in the palindrome changes, and when the middle digit of the starting palindrome of the block is 9. The first several unusual-length blocks are: zeroes from 9 to 10, ones from 99 to 100, ones from 191 to 201, ones from 292 to 302, ..., ones from 898 to 908, ones from 999 to 1000, ones from 1991 to 2001, ones from 2992 to 3002, and so on.
And here comes the final step. All such unusual-length blocks except the one from 9 to 10 consist of ones! Or, in other words, all blocks of zeroes have the same length within palindromes of the same amount of digits, except the block from 9 to 10.
Why? Because there's ten blocks between two consecutive palindromes with a 9 in the middle (with the only exception being 9 and 99), and ten is an even number. That's why every time we have a 9 in the middle, we start a block of ones.
And that allows us to calculate in one step the total amount of zeroes in the part of our infinite string that corresponds to one amount of digits in the palindrome. That means we can calculate the overall amount of zeroes in any segment in O(number of digits in the maximal palindrome) steps. Of course, we have to be careful near L and R.
And what about the amount of ones? It's equal to the total length minus the amount of zeroes :)
4. Modulo calculations
With the numbers in the input being quite big, the above calculations have to be performed carefully.
Some programming languages allow easy calculations with arbitrarily long numbers. But what if we use a language without this feature? Luckily, we're asked to find the answer modulo a (relatively) small number M.
That allows us to perform most calculations modulo M, and thus use only small numbers in those calculations. The calculations we need to find the answer are: addition, multiplication, subtraction and division by 2. The first three are performed in a standard way (first calculate the answer in integers, then take it modulo M). The fourth one is made possible by the fact that the modulo used in the problem is odd. When we divide a number X by 2 modulo M, we get just X/2 if X is even, and (X+M)/2 when x is odd. One can easily check that multiplying by 2 gets X back in both those cases.