Google Code Jam Archive — Round 2 2009 problems
Overview
Code Jam contestants never cease to surprise us, and their performance on this round was no exception. Our tough implementation problem proved to be so tough that only 10% more people solved it than our tough algorithmic problem; and so many people were familiar with the theorems needed for Problem C that 362 of you breezed right through it. Meanwhile Russia and East Asia dominated the top 10, with 9 out of the 10 top spots. But with all else said and done, first place was no surprise to anyone: ACRush, 2008 Code Jam Champion, finished all four problems less than halfway through the competition, and almost 30 minutes faster than everyone else.
Congratulations to the top 500 competitors, who will win a Code Jam t-shirt and advance to the next round!
Cast
Problem A. Crazy Rows Written by Cosmin Negruseri. Prepared by Igor Naverniouk and Marius Andrei.
Problem B. A Digging Problem Written by Mohamed Eldawy. Prepared by Ante Derek, Marius Andrei and Jonathan Wills.
Problem C. Stock Charts Written by Bartholomew Furrow. Prepared by Xiaomin Chen and Bartholomew Furrow.
Problem D. Watering Plants Written by John Dethridge. Prepared by Tomek Czajka and John Dethridge.
Contest analysis presented by Xiaomin Chen, Cosmin Negruseri, Bartholomew Furrow and John Dethridge.
Solutions and other problem preparation provided by Pablo Dal Lago, Petr Mitrichev, Fábio Moreira and Ruoming Pang.
A. Crazy Rows
Problem
You are given an N x N matrix with 0 and 1 values. You can swap any two adjacent rows of the matrix.
Your goal is to have all the 1 values in the matrix below or on the main diagonal. That is, for each X where 1 ≤ X ≤ N, there must be no 1 values in row X that are to the right of column X.
Return the minimum number of row swaps you need to achieve the goal.
Input
The first line of input gives the number of cases, T. T test cases follow.
The first line of each test case has one integer, N. Each of the next N lines contains N characters. Each character is either 0 or 1.
Output
For each test case, output
Case #X: Kwhere X is the test case number, starting from 1, and K is the minimum number of row swaps needed to have all the 1 values in the matrix below or on the main diagonal.
You are guaranteed that there is a solution for each test case.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1 GB.
1 ≤ T ≤ 60
Small dataset
1 ≤ N ≤ 8
Large dataset
1 ≤ N ≤ 40
Sample
3 2 10 11 3 001 100 010 4 1110 1100 1100 1000
Case #1: 0 Case #2: 2 Case #3: 4
B. A Digging Problem
Problem
The cave is on fire and there is smoke everywhere! You are trying to dig your way to the bottom of the cave where you can breathe. The problem is that there are some air holes inside the cave, and you don't want to fall too much or you will get hurt.
The cave is represented as an R x C matrix with air holes and solid rock cells. You start at position (1, 1), which is in the top-left corner. You can move one cell at a time, left or right, if that cell is empty (an air hole). After moving, if the cell below is empty, you fall down until you hit solid rock or the bottom of the cave. The falling distance must be at most F,or you will get hurt. You must reach the bottom of the cave without getting hurt. While falling you cannot move left or right.
You can also "dig", turning a cell that contains solid rock into an air hole. The cell that you dig can be one of two cells: the one to your right and below, or the one to your left and below. The cell above the one you are digging has to be empty. While falling you cannot dig.
Your goal is not only to get to the bottom of cave, but also to "dig" as few cells as possible.
Let's describe the operations with a concrete example:
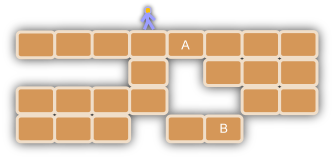
You start at (1, 1) and move right 3 times to position (1, 4), just like the picture.
You dig the rock at position (2, 5). Cell "A" becomes empty.
You move right one position and since there is no cell below you fall 3 cells to position (4, 5).
You dig the rock at position (5, 6). Cell "B" becomes empty.
You move right one position and since there is no cell below you fall 1 cell to position (5, 6).
You have reached the bottom of the cave by digging 2 cells.
Input
The first line of input gives the number of cases, N. N test cases follow. The first line of each case is formatted as
R C Fwhere R is the number of rows in the cave, C is the number of columns in the cave, and F is the maximum distance you can fall without getting hurt.
This is followed by R, rows each of which contains C characters. Each character can be one of two things:
- # for a solid rock
- . for an air hole
Output
For each test case, output one line in the format
Case #X: No/Yes [D]where X is the case number, starting from 1. Output "No" if you cannot reach the bottom of the cave. Output "Yes D" if the bottom of the cave can be reached and the minimum number of cells that need digging is D.
Limits
Memory limit: 1 GB.
1 ≤ N ≤ 50
1 ≤ F < R
Small dataset
Time limit: 40 seconds.
2 ≤ R ≤ 10
2 ≤ C ≤ 6
Large dataset
Time limit: 60 seconds.
2 ≤ R ≤ 50
2 ≤ C ≤ 50
Sample
3 2 2 1 .# ## 3 3 1 ... ### ### 3 2 1 .. #. ..
Case #1: No Case #2: Yes 3 Case #3: No
C. Stock Charts
Problem
You're in the middle of writing your newspaper's end-of-year economics summary, and you've decided that you want to show a number of charts to demonstrate how different stocks have performed over the course of the last year. You've already decided that you want to show the price of n different stocks, all at the same k points of the year.
A simple chart of one stock's price would draw lines between the points (0, price0), (1, price1), ... , (k-1, pricek-1), where pricei is the price of the stock at the ith point in time.
In order to save space, you have invented the concept of an overlaid chart. An overlaid chart is the combination of one or more simple charts, and shows the prices of multiple stocks (simply drawing a line for each one). In order to avoid confusion between the stocks shown in a chart, the lines in an overlaid chart may not cross or touch.
Given a list of n stocks' prices at each of k time points, determine the minimum number of overlaid charts you need to show all of the stocks' prices.
Input
The first line of input will contain a single integer T, the number of test cases. After this will follow T test cases on different lines, each of the form:
n k price0,0 price0,1 ... price0,k-1 price1,0 price1,1 ... price1,k-1 ... pricen-1,0 pricen-1,1 ... pricen-1,k-1
Where pricei,j is an integer, the price of the ith stock at time j.
Output
For each test case, a single line containing "Case #X: Y", where X is the number of the test-case (1-indexed) and Y is the minimum number of overlaid charts needed to show the prices of all of the stocks.
Limits
Memory limit: 1 GB.
1 ≤ T ≤ 100
2 ≤ k ≤ 25
0 ≤ pricei,j ≤ 1000000
Small Input
Time limit: 20 seconds.
1 ≤ n ≤ 16
Large Input
Time limit: 30 seconds.
1 ≤ n ≤ 100
Sample
3 3 4 1 2 3 4 2 3 4 6 6 5 4 3 3 3 5 5 5 4 4 6 4 5 4 5 2 1 1 2 2 5 4 4 4 4 1
Case #1: 2 Case #2: 3 Case #3: 2
D. Watering Plants
Problem
In your greenhouse you have a number of plants which you need to water.
Each of the plants takes up an area which is a circle. No two of the plants overlap or touch each other.
You are going to buy two sprinklers. Each of the sprinklers will spray everything within a circle of radius R with water.
One of the sprinklers will run in the morning, and one will run at night. For you to be satisfied that a plant will get enough water, either the whole area of the plant must be watered in the morning, or the the whole area of the plant must be watered at night. So each of the circles representing a plant must be completely in one or both of the two circles representing the area the sprinklers can water.
Given the location and radius of each of the plants, find the minimum radius R so that it is possible to place the two sprinklers to water all the plants. The sprinklers will be installed on the ceiling, so a sprinkler's position can be inside the area of a plant.
Input
- One line containing an integer C, the number of test cases in the input file.
- One line containing N, where N is the number of plants you have.
- N lines, one for each plant, containing three integers "X Y R", where (X, Y) are the coordinates of the center of the plant, and R is the radius of the plant.
Output
For each test case:
- One line containing the string "Case #x: R" where x is the number of the test case, starting from 1, and R is the minimum radius of the sprinklers.
Limits
Memory limit: 1 GB.
All numbers in the input file are integers.
1 ≤ X ≤ 1000
1 ≤ Y ≤ 1000
1 ≤ R ≤ 100
Small Input
Time limit: 30 seconds.
1 ≤ C ≤ 10
1 ≤ N ≤ 3
Large Input
Time limit: 60 seconds.
1 ≤ C ≤ 30
1 ≤ N ≤ 40
Sample
2 3 20 10 2 20 20 2 40 10 3 3 20 10 3 30 10 3 40 10 3
Case #1: 7.000000 Case #2: 8.000000
In the first case, a sprinkler of radius at least 7 centered at (20,15) will water the first two plants. A sprinkler of radius at least 3 will water the plant at (40,10).
In the second case, one of the two sprinklers will need a radius of at least 8. Note that the plant at (30,10) must be covered entirely by one of the two sprinklers.
Analysis — A. Crazy Rows
Reformulation of the problem
It is easy to see, for each row, only the position of the last '1' matters. We can re-formulate the problem
CR: Given a list of numbers (a0, ... aN-1). You are allowed to swap adjacent numbers. Find the minimum number of swaps needed so that the i-th number is at most i in the final configuration.
The well known special case
Perhaps many of you know the following special case.CR*: Given a permutation (x0, ... xN-1) of the numbers 0 to N-1. You are allowed to swap adjacent numbers. Find the minimum number of swaps needed in order to sort the list in increasing order.Perhaps you also know the complete solution to CR*. It is very simple and elegant, and important to our problem. So we produce here.
Solution (to CR*). Define the disorder of the list to be the number of pairs i < j, where xi > xj. In one swap (of adjacent numbers), the total number of disorder is changed by exactly one. (Check it!) Therefore, let the disorder of initial configuration be D, you need at least D swaps. D swaps is also sufficient -- as long as the list is not sorted, there exist adjacent pairs in wrong order. You can swap any of such pairs and decrease the disorder by 1. ◊
In particular,
(1) One type of optimal solutions of CR* involves first to swap the number 0 all the way to the left, then let it stay there forever.
Solution to our problem
Imagine we know which of the ai's will finally go to position 0, and which one will go to position 1, etc., then we can simply use the algorithm for CR*. But there might be multiple candidates for a single position. For example, there might be several i's such that ai = 0, and even some ai = -1.
Below is the judge's C++ solution. b[i] is the "decoded" position where a[i] will be in the final configuration. The algorithm says: For those candidates for position 0, pick the leftmost one. Then in the rest, for those candidates for position 1, pick the leftmost one. And so on.
// -1 means no position is assigned for a[j].
for(i=0;i<N;i++) b[j]=-1;
for(i=0;i<N;i++) {
for(j=0;j<N;j++) if(b[j]<0 && a[j]<=i) {
b[j]=i; break;
}
}
int r=0;
for(i=0;i<N;i++) for(j=i+1;j<N;j++)
if(b[i]>b[j]) r++;
// output r as the answer
Note that, once the b[i]'s are fixed, you only need to count the disorders as in CR*; no real swapping needs to be simulated.
Proof of our solution
The key observation is, for multiple candidates for position 0, you will never need to swap any two of them. Suppose you do swap, say u and v, both are at most 0. I can simply ignore it, and pretend that they are swapped (i.e., exchange the roles of u and v thereafter). The final configuration is still a good one. Thus we proved that, for all the candidates for position 0, the leftmost one, call it u*, will finally go to position 0.
Now, imagine we have decoded the final positions for every one. Then (1) tells us that there is one solution where we first move u* all the way to the left, and never worry about it again. Therefore we now face the next question: Which of the rest of the numbers should go to position 1?
This is exactly the same problem, but with one number fewer. ◊
Analysis — B. A Digging Problem
The setup of this problem, where you can go left, right and down but never up hints that some dynamic programming solution is the way to go, but the details are a bit involved.
When we're on a row we need to know which are the rock cells that were dug previously so that we know how much we can move left or right. This means that we could have a state in our algorithm be (i, j, air_holes) where i is the current row, j is the current column and air_holes is the set of cells on row i that were dug previously or were empty. Filling the values for these states in the whole matrix would take exponential time as air_holes can take on as many as 2^C values. This would be enough to solve the small input, but for the large we need to improve our algorithm a bit.
First let's observe that it only makes sense to dig out cells that will form a connected empty zone. After we fall one row, we'll be able to use just the current zone of empty boxes. Now our state is (i, j, start, end) where start is the starting column index of the current empty zone and end is the index of the zone's end column. This idea yields a polynomial solution, as we have O(R * C^3) possible states and there are at most C^2 different states that we can create on the next row.
But we can improve on this solution. It doesn't make sense to change directions after we started to dig; if we're moving right, it doesn't matter how many empty cells we have on the left. This changes the state to (i, j, dir, count) where dir is the current direction (left or right), and count is the number of empty cells in that direction. This reduces the state space to O(R * C^2).
The implementation details are somehow tricky, and you have to make sure you don't fall more than F steps -- a detail we've skipped here. There are many possible ways to implement this problem, some of which result in much simpler code than others. We encourage you to download and study various correct implementations from the scoreboard.
Before the contest began, we evaluated this problem as the second easiest in the contest; but the many details needed to solve it resulted in this problem having the second-smallest number of successful solutions.
Something related
If you are among our older contestants, this problem may bring back sweet memories of the classic game Lode Runner, and perhaps memories of many happy days associated with it.
Analysis — C. Stock Charts
It will come as no great surprise, but the author of this problem came up with it while reading a local newspaper's end-of-year economics summary, seeing a number of overlaid charts in it and then wondering how to minimize the number of charts needed.
Charts and DAGs
Consider two simple charts: A and B. They can be related to each other in one of three ways: all of A's values can be strictly less than all of B's values (A < B), in which case they can appear on the same overlaid chart; their lines can cross (A \ B), in which case they can't appear on the same overlaid chart; or all of A's values can be strictly greater than all of B's values (A > B), in which case they can appear on the same overlaid chart.
Given this sort of relationship we can construct a graph, where the nodes are simple charts and there is an edge from A to B iff A > B. This gives us a directed, acyclic graph that is its own (non-reflexive) transitive closure. Any directed path in the DAG represents a valid composite chart. To solve the problem, then, we want to find the minimum number of paths that we need so that all nodes are part of exactly one path.
How would we find the paths? We may start from a chart that is relatively high, then find one below it, and keep adding lower charts, until we cannot find more. This completes our first overlaid charts. We start the same process for the second path, and so on. In any step, there might be several choices for the next chart we can use. In order to minimize the number of paths, we need to make a good choice in each step.
Now, behold, the Aha moment of this problem.
Solution from maximum matching
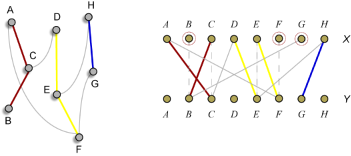
For the DAG with n points, we make a bipartite graph with n points on each side. Draw an edge from XA to YB if the relation A > B holds, i.e., B can be the next chart below A. Observe (yes, you really need to see it, instead of hear it!) how any path in the DAG corresponds to a series of edges in the bipartite graph; and how any matching of the bipartite graph corresponds to a way to partition the DAG into paths. Any unmatched point XA on the left side corresponds to the lowest point on a path (the lowest chart on an overlaid graph). Each path has exactly one such point. We want to minimize the number of paths, the same as minimizing the number of unmatched points on the left side. That is, we want to find the maximum matching in a bipartite graph.
Here is the judge's solution in C++.
namespace Solver {
int N,K;
bool cbn[111][111]; // can be next
int prev[111];
bool visited[111];
bool FindNextDfs(int a) {
if(a<0) return true;
if(visited[a]) return false;
visited[a]=true;
for (int i=0;i<N;i++) if(cbn[a][i]) {
if(FindNextDfs(prev[i])) {
prev[i]=a;
return true;
}
}
return false;
}
int Solve(const vector<vector<int> >& stock) {
N=stock.size(); K=stock[0].size();
int i,j,k;
for(i=0;i<N;i++) {
for(j=0;j<N;j++) {
if(i==j) cbn[i][j]=false;
else {
cbn[i][j]=true;
for(k=0;k<K;k++)
if(stock[i][k]<=stock[j][k]) cbn[i][j]=false;
}
}
}
memset(prev, -1, sizeof(prev));
int ret=0;
for(i=0;i<N;i++) {
memset(visited, 0, sizeof(visited));
if(!FindNextDfs(i)) ret++;
}
return ret;
}
Note that this is indeed the bipartite matching program. We named the variables as if we are really constructing the set of paths and unaware of the bipartite graph. In fact, it's a worthy exercise to go over this without bipartite matching in your mind.
This completes the solution of our problem. But we may continue with more stories.
Theoretical background
In combinatorics, DAGs are called partially ordered sets, or posets. A directed path is called a chain in the poset. An independent set in the DAG, corresponding to a set of points where no '>' relation holds between any two of them, is called an anti-chain. Our problem is then, given a poset, find the minimum number of chains needed to cover all the points.
If we see an anti-chain of size α, we need at least α chains to cover the set, because each chain can contain at most one of these points. Suppose we find the maximum anti-chain to be of size α*, we know the answer must be at least α*. Is this enough though?
We are ready to introduce one of the classical theorems in combinatorics.
Theorem (Dilworth 1950) In a poset, the minimum number of chains needed to cover the whole set equals the size of the biggest anti-chain.
Dilworth's theorem is closely related to other classical theorems in combinatorics. In fact it is equivalent to Hall's marriage theorem on bipartite graphs, and the max-flow-min-cut theorem.
The number in Dilworth's theorem is (naturally) called the width of the poset. Our algorithm above thus finds the width of a poset. Interested readers might find, in our input file, perturbed copies of the following posets:
- The complete Boolean lattice: All the 2k subsets of a k-element set, where A > B if B is a subset of A. All the ⌈k/2⌉-subsets form a maximum anti-chain of size (k choose ⌈k/2⌉), and indeed we can partition the Boolean lattice into this many chains. (This is called the Sperner's theorem.)
- All the integers from 1 to n, A > B if A is a multiple of B. The set of all the prime numbers seems to be a big anti-chain. But it is not big enough. We leave it as an exercise to prove that the width of this poset is ⌈n/2⌉.
More information
Partially ordered set - Dilworth's theorem
Analysis — D. Watering Plants
This problem involves finding circles that enclose other circles. The problem of finding a circle surrounding a set of points is the fairly well-known minimal enclosing circle problem, but changing the points to circles makes the problem slightly trickier.
One solution is to do a binary search to find the minimum sprinkler radius. This reduces the problem to the problem of determining whether two sprinklers of a given radius can cover all the plants. To solve this, we can make the assumption that any sprinkler used in the solution either:
- covers exactly one plant, or
- the boundary of the sprinkler touches the boundary of at least two of the plants it covers.
- a sprinkler centered on each plant, and
- for each pair of plants, the set of sprinklers covering those plants and touching their boundary (there are 0, 1, or 2 of these per pair.)
A second solution is to directly find the minimum sprinkler radius. To do this, we can use a slightly different simplifying assumption -- that every sprinkler either:
- covers exactly one plant (using the same radius as the plant),
- covers two plants which touch the edge of the sprinkler and whose centers are collinear with the center of the sprinkler, or
- covers three plants which touch the edge of the sprinkler.
Finding the circle which touches 3 given circles is harder than the equivalent problem for 3 points. Here are three possible approaches:
- The set of points where a sprinkler can be centered in order to touch two plants is a hyperbola, so we could algebraically compute the intersection of two of those hyperbolae.
- We can use a gradient-descent approach to find numerically the point minimizing the function from potential centers of sprinklers to the radius required for a sprinkler centered at that location to cover all three plants.
- We can subtract from the radius of each of the three plants the radius of the smallest plant, then compute an inversion about that plant's center. Then we find appropriate tangents to the two inverted plants, re-invert to find the corresponding circle, and add back the radius of the smallest plant.