Google Code Jam Archive — APAC Semifinal 2008 problems

The Simple Solution

Let us visualize this problem. Each animal is characterized as a pair (H, W), which can be viewed as a point in the two dimensional Cartesian coordinate system. For each animal that is known to be a bird, we color it red. For each animal known to be a non-bird, we color it blue. The problem states that there exists a rectangle such that a point is red if and only if it is in the rectangle. The problem is trivial if there are no red points. From now on we assume there are red points.

For any two distinct points U and V, there is naturally a rectangle determined by U and V. It is the smallest rectangle containing both U and V, with the four corners U, V, (H_U, W_V), and (H_V, W_U). When U and V are on the same horizontal or vertical line, the rectangle degenerates to a segment. Formally, the rectangle contains all the points (H, W) such that

(|H - H_U| + |W - W_U|) + (|H - H_V| + |W - W_V|) = |H_U - H_V| + |W_U - W_V|.

We have the following proposition.

If U and V are two red points, and R be the rectangle determined by U and V; then any point in R must also be red, since any rectangle containing both U and V must contain R.

For the set of all red points in the input, there is also naturally a smallest rectangle, R₀, that contains all of them. There are different ways to define this rectangle:

• (a) The intersection of all the rectangles that contain all the red points.
• (b) The union of all the rectangles determined by U and V, where (U, V) range over all the red point pairs.
• (c) The rectangle with four corners A=(H_min, W_min), B=(H_min, W_max), C=(H_max, W_min), and D=(H_max, W_max), where the min and max are taken over all the red points.

The interested reader may check the equivalence of the above definitions.

Now, given a point X, we want to know if it is a bird or not. Clearly, if X is inside R₀, then it must be bird. Otherwise, we may pretend it is red, and compute the new rectangle R' based on (c). This can be done in a constant number of comparisons. If there is a blue point from the input that lies in R', then X must not be a bird. Otherwise, X might (taking R' as the red rectangle) or might not (taking R₀ as the red rectangle) be a bird.

By the limits of this problem, a Θ(NM) algorithm is fast enough. That is, we simply take any blue input point, and check if that is inside R'.

Further Discussion

Another way to view the last step of the solution, when the query point X is given, is to see whether there is a known red point Y such that the rectangle determined by X and Y contains any blue point. It is enough to check Y = A, B, C, or D as in (c). To check this, we do not need to go over all the blue input points. There are standard pre-processing techniques that can reduce the query time from N to log N.

For example, for A, we can define two sets based on the blue inputs: those points that are higher (along the W-axis) than A (call them A₁) and the rest of the A points (A₂ = A - A₁). The task of determining whether there is a blue point between X and A becomes the query of lowest or highest point in the range between H_X and H_A.

This problem is a sheep in wolf's clothing. However, it must have been very convincing wolf's clothing! Fewer competitors solved it than any other problem, despite the simplicity of the actual solution. Since this was an onsite round, they were all experienced competitors; in some sense, that worked against them.

Why does the problem seem so hard? To a practiced eye, it has all the trappings of a horrible exponential search. You have 5 actions to choose from on each day, and the results of those actions don't tend to overlap, leading to an exponential number of possible states. Furthermore, even the subtlest change in a nation's strength can drastically affect the final outcome, so at each step the entire state of the world matters. This makes a Dynamic Programming-based solution look unlikely. And due to the chaotic nature of the rules, there's unlikely to be a greedy strategy that works in all cases.

So a horrible exponential search seems essential. On a 50x50 grid of numbers between 0 and 1000, this is clearly intractable! Give up and go home. No, wait... it's supposed to be solvable somehow, right? How could that be?

Well, if you try a few cases by hand, you'll soon realize why: everyone ends up killing their neighbors really, really quickly. A random map tends to stabilize (no living neighbors) in only 4-6 days. It's actually very difficult to come up with a case that takes longer. The more you try, the more you'll realize just how difficult it is; the army sizes required grow exponentially, and the tighter you pack them the sooner they all die. The map size doesn't turn out to matter much - it's the army size bound of 1000 that really sets the cap on how long you'll need to search.

What exactly is this cap? That's a really tough question. For instance, if army sizes are unbounded, there is no small limit. Here's a simple (2n-2)x2 case that takes n days to stabilize:
1 2 4 8 ... 2^2n-3
1 2 4 8 ... 2^2n-3

However, the army sizes must grow exponentially relative to the number of days. Here's a simple proof: on day n, let S_n be the strength of the strongest nation that still has living neighbors. Let N be any nation with strength ≥ S_n/2. Suppose that after 8 days N still has strength ≥ S_n/2. Then it must have killed all its neighbors, since none had strength ≥ S_n (that is, any neighbor would die after at most 2 attacks). So every such N either ends up isolated or weaker than S_n/2 after 8 days. Thus, S_n+8 ≤ S_n/2. This puts a strict bound of 8(log₂S_n+1) more days before all nations are dead or isolated.

Unfortunately, for army sizes of 1000 this bound of 80 days still isn't very helpful. The bound can be improved with tighter reasoning, but due to the compact, constrained nature of the grid, the "true" bound is probably much smaller - around 9-10 days! However, we don't know how to prove a bound anywhere near this. If you can think of a way, let us know! :)

The worst test case in our data had an answer of "9 day(s)". So as it turns out, even a straight brute force solution (on the worst-case order of 50x50x5⁹) would suffice to solve it. Adding simple pruning heuristics and memoization can potentially also help, but isn't necessary.

Incidentally, one potential coding error you could make is to assume that effects can only propagate at one grid square per day. The "speed of light" (as it's known in cellular automata) is actually two grid squares per day, because if an army's neighbor changes, it may choose to attack its opposite neighbor instead. In the "9 day(s)" test case, there are nations 13 squares away from yours that end up affecting the answer. So if you tried to speed up your solution by considering only the local region around your nation, you'd have to be careful not to make it too local.

In the end, all it took to get this problem was bravery (or foolishness). If you code it properly and try it, it works! It's just a question of how well you can convince yourself that the simple solution has a hope of working. You certainly wouldn't want to download the Large dataset and then realize your solution was too slow...

The problem explicitly states that the contestant has an infinite number of degrees of freedom. She can bet ANY fraction of her current amount. This makes it impossible to brute force over all of the possible bets. The trick is to discretize the problem.

Following one of the principles in problem solving, we look at the easier cases. The problem is easy if there is one round. We suggest you do it for the case when there are two rounds. It is not hard, but it reveals the interesting nature of the problem. The figure below illustrates the situation in the second-to-last round, the last round and after the last round.

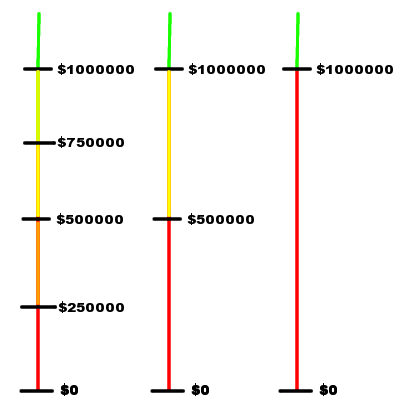
The colors represent different probability zones. All sums in a probability zone share the same probability of winning. The important sums are marked and labeled.

If we know the probability of winning for all sums in the next round P_next(sum), then the probability of winning in this round is:

p * P_next(sum + stake) + (1 - p) P_next(sum - stake),

where stake is the amount we are betting.

Now, given the existence and location of the important sums in the next round, we can find the locations of the important sums in this round. The figure below illustrates how we find these sums. The midpoints between the important sums of the next round become important in this round. I.e in the case of the green point in figure 2, we can move up by lowering the stake, and we can move down by increasing the stake, without changing the end probability. The probability of the blue, green and red points is the same. This also illustrates that the probability in a 'probability zone' which is limited by two important sums is equal to the probability at the lower important sum.

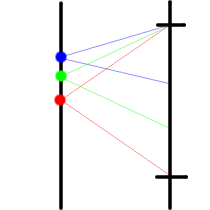
Conclusion: The important sums of round i are the union of the important sums of round (i+1) and their midpoints. We need to consider $0 an important sum in the last round because we can't bet more than we have.

Now, we only need to compute probabilities at the important sums, bootstrapping at 1.0 for $1000000, and 0.0 for $0 in the last round. Then, going backwards, we fill the probabilities at the important sums in the previous rounds.

By the limits of the input, we may try all the stakes that lead to important points in the next round. It is an interesting question whether there are mathematical properties that could reduce the complexity of this computation, but that is beyond the scope of this analysis.

This problem is a classical graph problem called subtree isomorphism. As an interesting note, the modern era in art history actually starts far earlier than the so called classical period in computer science.

In this problem, we are given two trees T₁ and T₂. We are going to decide if T₂ is isomorphic to any subtree of T₁. The general sub-graph isomorphism problem is notoriously hard. But as you perhaps have seen many times, when the things come to trees, it is very solvable. The problem is actually well studied, and is a standard exercise in algorithm design.

First, a bit of terminology. Just for convenience, in our discussion, for two rooted trees, we say one fits into the other if there us an isomorphism that maps the former to a subtree of the latter such that the root is mapped to the other's root.

We may fix T₂ and consider it as a tree rooted at vertex 0. We do not know which vertex of T₁ corresponds to 0 of T₂ in the isomorphism. But we may try each vertex in T₁, and see if T₂ fits into T₁.
For a concrete example, let's say we root T₁ at vertex x. Assume that there are 3 children of 0 in T₂ -- y₁, y₂, and y₃. Assume that there are 5 children of x in T₁ -- x₁. x₂, x₃. T₂ fits into T₁ if and only if we can find that the subtree at y₁ fits into the subtree at x_i for some i, the subtree at y₂ fits into the subtree at x_j for some other j ≠ i, and the subtree at y₃ fits into the subtree at x_k for some k ≠ i, k ≠ j.

The solution for this problem as follows. Once we have fixed the root x, each vertex has a level in its tree. For each vertex u in T₁ and v in T₂, if they have the same level (just a bit of reasonable optimization, not necessary for this problem), we want to decide if the subtree at v fits into the subtree at u. We do this from bottom up, the deeper levels first.
For any such pair (u, v) with children { u_i | i = 1,2,... } and { v_j | j = 1,2,... }, we know which v_j fits into which u_i since we are doing the computations bottom up. We find a fit if and only if we can find, for each v_j, a distinct u_i such that v_j fits into u_i. This is clearly a bipartite graph matching problem.

We leave it an exercise to prove that the algorithm, runs in O(N²M²) time. There are algorithms with better complexities. For interested readers, we refer to the following paper
R. Shamir, D. Tsur, "Faster Subtree Isomorphism", Journal of Algorithm, 33, 267-280 (1999).
which contains a recent result as well as references to earlier works.

More information

Subtree Isomorphism - Graph Isomorphism - Bipartite Matching