Google Code Jam Archive — Round 3 2008 problems
Overview
The last online round of Google Code Jam 2008 turned out to be an exciting feast of dynamic programming, plane geometry, discrete geometry, basic graph search, bipartite matching, combinatorics and number theory -- all in the time span of two hours. The problems got more challenging, and the contest more and more exciting.
Before the game, our own Tomek Czajka took a look at the problems and made some amazing conjectures about the contest statistics. One of them was that the first person would complete all the problems in 100 minutes. This conjecture was proved by bmerry in a very nice way. All the problems were finished at the 98th minute. In addition, bmerry add 4 minutes of penalty for a wrong submission. The only other player with a perfect score was yuhch123, a Chinese high school student, with a correct submission in the last 5 minutes of the contest.
In 3rd position was halyavin, seemingly only seconds away from the last submission. In the last 5 minutes, many contestants (including 13 of the top 20) submitted something correct.
Credits
Problem A. How Big Are the Pockets? Written and prepared by Xiaomin Chen.
Problem B. Portal Written by Mohamed Eldawy. Prepared by Frank Chu and Mark Gordon.
Problem C. No Cheating Written by Yintao Yu. Prepared by Mark Gordon and Yintao Yu.
Problem D. Endless Knight Written by Junbin Teng. Prepared Xiaomin Chen.
Contest analysis presented by Xiaomin Chen and Cosmin Negruseri.
A. How Big Are the Pockets?
Problem
Professor Polygonovich, an honest citizen of Flatland, likes to take random walks along integer points in the plane. He starts from the origin in the morning, facing north. There are three types of actions he makes:
- 'F': move forward one unit of length.
- 'L': turn left 90 degrees.
- 'R': turn right 90 degrees.
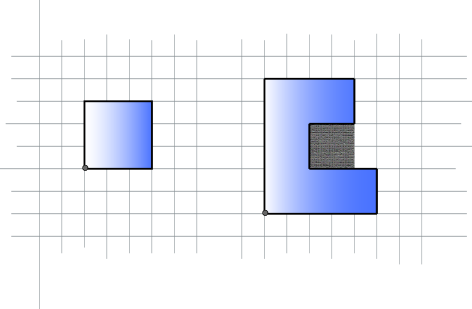
At the end of the day (yes, it is a long walk!), he returns to the origin. He never visits the same point twice except for the origin, so his path encloses a polygon. In the following picture the interior of the polygon is colored blue (ignore the points x, y, z, and w for now; they will be explained soon):

Notice that as long as Professor Polygonovich makes more than 4 turns, the polygon is not convex. So there are pockets in it.
Warning! To make your task more difficult, our definition of pockets might be different from what you may have heard before.
The gray area below indicates pockets of the polygon.

Formally, a point p is said to be in a pocket if it is not inside the polygon, and at least one of the following two conditions holds.
- There are boundary points directly both east and west of p; or
- There are boundary points directly both north and south of p.
Boundary points are the points traversed by Mr. Poligonovich on his walk (these include all points, not just those with integer coordinates).
Consider again the first picture from above. Point x satisfies the first condition; y satisfies both; z satisfies the second one. All three points are in pockets. The point w is not in a pocket.
Given Polygonovich's walk, your job is to find the total area of the pockets.
Input
The first line of input gives the number of cases, N. N test cases follow.
Each test case has the description of one walk of Professor Polygonovich. It starts with an integer L. Following are L "S T" pairs, where S is a string consisting of 'L', 'R', and 'F' characters, and T is an integer indicating how many times S is repeated.
In other words, the input for one test case looks like this:
S1 T1 S2 T2 ... SL TL
The actions taken are the concatenation of T1 copies of S1, followed by T2 copies of S2, and so on.
The "S T" pairs for a single test case may not all be on the same line, but the strings S will not be split across multiple lines. The second example below demonstrates this.
Output
For each test case, output one line containing "Case #X: Y", where X is the 1-based case number, and Y is the total area of all pockets.
Limits
Time limit: 60 seconds per test set.
Memory limit: 1GB.
1 ≤ N ≤ 100
1 ≤ T (bounded from above by constraints in the problem statement,
"Small dataset" and "Large dataset" sections)
The path, when concatenated from the input strings, will not have two
consecutive direction changes (that is, there will be no 'LL', 'RR', 'LR', nor
'RL' in the concatenated path). There will be at least one 'F' in the path.
The path described will not intersect itself, except at the end, and it will
end back at the origin.
Small dataset (Test set 1 - Visible)
1 ≤ L ≤ 100
The length of each string S will be between 1 and 16, inclusive.
The professor will not visit any point with a coordinate bigger than 100 in
absolute value.
Large dataset (Test set 2 - Hidden)
1 ≤ L ≤ 1000
The length of each string S will be between 1 and 32, inclusive.
The professor will not visit any point with a coordinate bigger than 3000 in
absolute value.
Sample
2 1 FFFR 4 9 F 6 R 1 F 4 RFF 2 LFF 1 LFFFR 1 F 2 R 1 F 5
Case #1: 0 Case #2: 4
The following picture illustrates the two sample test cases.
B. Portal
Problem
PortalTM is a first-person puzzle/platform game developed and published by Valve Software. The idea of the game was to create two portals on walls and then jump through one portal and come out the other. This problem has a similar idea but it does not assume you have played Portal.
For this problem you find yourself in a R by C grid. Additionally there is a delicious cake somewhere else in the grid. You're very hungry and wish to arrive at the cake with as few moves as possible. You can move north, south, east or west to an empty cell. Additionally, you have the ability to create portals on walls.
To help you get to the cake you have a portal gun which can shoot two types of portals, a yellow portal and a blue portal. A portal is created by shooting your portal gun either north, south, east or west. This emits a ball of energy that creates a portal on the first wall it hits. Note that for this problem shooting the portal gun does not count as a move. If you fire your portal gun at the cake, the energy ball will go right through it.
After creating a yellow portal and a blue portal, you can move through the yellow portal to arrive at the blue portal or vice versa. Using these portals you may be able to reach the cake even faster! You can only use portals after you create both a yellow and a blue portal.
Consider the following grid:
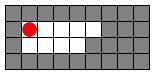
Gray cells represent walls, white cells represent empty cells, and the red circle indicates your position.
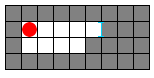
Suppose you shoot a blue portal east. The portal is created on the first wall it hits, resulting in:
Now suppose you shoot a yellow portal south:
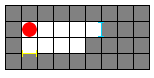
Next you move south once:
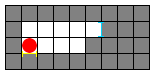
Now comes the interesting part. If you move south one more time you go through the yellow portal to the blue portal:
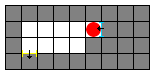
There can only be one yellow portal and one blue portal at any time. For example if you attempt to create a blue portal to the west the other blue portal will disappear:
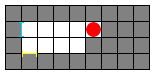
A portal disappears only when another portal of the same color is fired.
Note that the portals are created on one side of the wall. If a wall has a portal on its east side you must move into the wall from the east to go through the portal. Otherwise you'll be moving into a wall, which is improbable.
Finally, you may not put two portals on top of each other. If you try to fire a portal at a side of a wall that already has a portal, the second portal will fail to form.
Given the maze, your initial position, and the cake's position, you want to find the minimum number of moves needed to reach the cake if it is possible. Remember that shooting the portal gun does not count as a move.
Input
The first line of input gives the number of cases, N. N test cases follow.
The first line of each test case will contain the integers R and C separated by a space. R lines follow containing C characters each, representing the map:
.indicates an empty cell;#indicates a wall;Oindicates your starting position; andXindicates the cake's position.
There will be exactly one O and one X character per
case.
Cells outside of the grid are all walls and you may use them to create portals.
Output
For each test case you should output one line containing "Case #X: Y" (quotes for clarity) where X is the number of the test case and Y is the minimum number of moves needed to reach the cake or "THE CAKE IS A LIE" (quotes for clarity) if the cake cannot be reached.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
Small dataset (Test set 1 - Visible)
N = 200
1 ≤ R, C ≤ 8
Large dataset (Test set 2 - Hidden)
N = 50
1 ≤ R, C ≤ 15
Sample
3 4 7 .O..##. .#..... .#.#### .#...X. 5 5 O.... ..... ..... ..... ....X 1 3 O#X
Case #1: 4 Case #2: 2 Case #3: THE CAKE IS A LIE
Here is the sequence of moves for the first case (note that shooting the portal gun does not count as a move):
- Move one step east.
- Shoot a blue portal north.
- Shoot a yellow portal south.
- Move one step north through the blue portal.
- Shoot a blue portal east.
- Move one step south through the yellow portal.
- Move one step west.
- Eat your delicious and moist cake.
PortalTM is a trademark of Valve Inc. Valve Inc. does not endorse and has no involvement with Google Code Jam.
C. No Cheating
Problem
A local high school is going to hold a final exam in a big classroom. However, some students in this school are always trying to see each other's answer sheet during exams!
The classroom can be regarded as a rectangle of M rows by N columns of unit squares, where each unit square represents a seat.
The school principal decided to set the following rule to prevent cheating:
Assume a student is able to see his left, right, upper-left, and upper-right
neighbors' answer sheets. The assignment of seats must guarantee that nobody's
answer sheet can be seen by any other student.
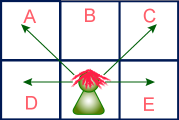
As in this picture, it will not be a good idea to seat anyone in A, C, D, or E because the boy in the back row would be able to see their answer sheets. However, if there is a girl sitting in B, he will not be able to see her answer sheet.
Some seats in the classroom are broken, and we cannot put a student in a broken seat.
The principal asked you to answer the following question: What is the maximum number of students that can be placed in the classroom so that no one can cheat?
Input
The first line of input gives the number of cases, C. C test cases follow. Each case consists of two parts.
The first part is a single line with two integers M and N: The height and width of the rectangular classroom.
The second part will be exactly M lines, with exactly N characters in each of these lines. Each character is either a '.' (the seat is not broken) or 'x' (the seat is broken, lowercase x).
Output
For each test case, output one line containing "Case #X: Y", where X is the case number, starting from 1, and Y is the maximum possible number of students that can take the exam in the classroom.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
C = 20
Small dataset (Test set 1 - Visible)
1 ≤ M ≤ 10
1 ≤ N ≤ 10
Large dataset (Test set 2 - Hidden)
1 ≤ M ≤ 80
1 ≤ N ≤ 80
Sample
4 2 3 ... ... 2 3 x.x xxx 2 3 x.x x.x 10 10 ....x..... .......... .......... ..x....... .......... x...x.x... .........x ...x...... ........x. .x...x....
Case #1: 4 Case #2: 1 Case #3: 2 Case #4: 46
D. Endless Knight
Problem
In the game of chess, there is a piece called the knight. A knight is special
-- instead of moving in a straight line like other pieces, it jumps in an "L"
shape. Specifically, a knight can jump from square (r1, c1) to (r2, c2) if and
only if
In this problem, one of our knights is going to undertake a chivalrous quest of moving from the top-left corner (the (1, 1) square) to the bottom-right corner (the (H, W) square) on a gigantic board. The chessboard is of height H and width W.
Here are some restrictions you need to know.
- The knight is so straightforward and ardent that he is only willing to move towards the right and the bottom. In other words, in each step he only moves to a square with a bigger row number and a bigger column number. Note that, this might mean that there is no way to achieve his goal, for example, on a 3 by 10 board.
- There are R squares on the chessboard that contain rocks with evil power. Your knight may not land on any of such squares, although flying over them during a jump is allowed.
Your task is to find the number of unique ways for the knight to move from the top-left corner to the bottom-right corner, under the above restrictions. It should be clear that sometimes the answer is huge. You are asked to output the remainder of the answer when divided by 10007, a prime number.
Input
Input begins with a line containing a single integer, N. N test cases follow.
The first line of each test case contains 3 integers, H, W, and R. The next R lines each contain 2 integers each, r and c, the row and column numbers of one rock. You may assume that (1, 1) and (H, W) never contain rocks and that no two rocks are at the same position.
Output
For each test case, output a single line of output, prefixed by "Case #X: ", where X is the 1-based case number, followed by a single integer indicating the number of ways of reaching the goal, modulo 10007.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
1 ≤ N ≤ 100
0 ≤ R ≤ 10
Small dataset (Test set 1 - Visible)
1 ≤ W ≤ 100
1 ≤ H ≤ 100
1 ≤ r ≤ H
1 ≤ c ≤ W
Large dataset (Test set 2 - Hidden)
1 ≤ W ≤ 108
1 ≤ H ≤ 108
1 ≤ r ≤ H
1 ≤ c ≤ W
Sample
5 1 1 0 4 4 1 2 1 3 3 0 7 10 2 1 2 7 1 4 4 1 3 2
Case #1: 1 Case #2: 2 Case #3: 0 Case #4: 5 Case #5: 1
Analysis — A. How Big Are the Pockets?
(i). Computing the area of the polygon
As Polygonovich walks, the interior of the polygon either always stays on his right side, or always on his left side. This is by no means a trivial fact. The polygon can be so complicated that given a poriton of the walk in the middle, one has no way to decide whether the left side is the interior, or the right side is. Let us accept this fact and assume the former case -- his right hand always touches the interior of the polygon.
Fix a vertical bar of unit width, observe the interaction between P, Polygonovich's walk, and B, the vertical bar.
- P crosses B an even number of times. Because the walk is closed, and any time Polygonovich crosses from the left to the right, the next time he must cross in the other direction. From top down, we label them as the 1st crossing, the 2nd one, and so on.
-
Furthermore, look down at B from high above. In the beginning, it is outside
the polygon. Every time it encounters an edge of P, it changes from being
outside the polygon to being inside and vice versa. So, a unit square on B
is inside the polygon if and only if it is between some
(2k-1)-st crossing and(2k)-th crossing. -
Note that if the polygon is always on the right-hand side, then we know that
the
(2k-1)-st crossing is always from left to right, and the(2k)-th one is from right to left.
Given any unit square U, we can decide whether it is in the polygon by counting the number of left-to-right crossings vertically above U, minus the number of right-to-left crossings above U. We can have a little counter inside U, and each time there is a left-to-right crossing above U, we increase the counter by 1; and for the right-to-left crossings, decrease the counter by 1.
After these mental exercises, we make the final jump back to the interaction between P and B. We may imagine a bounding box outside the polygon so that there are finitely many counters, and we now consider the area, it is nothing other than the summation of all the counters. To compute the area, we do the following.
Set A = 0 in the beginning. Walk along P, for each horizontal edge from left to right at height h, we increment A by h. This is the effect of this edge on all the counters for the unit squares below. And for each edge from right to left at height h, we decrement A by h.
All the time we assume the interior is always on the right hand side. In the opposite case, the highest edge on each bar will be a right-to-left cross, and all of the reasoning above is similar with only a difference in signs. So if we ever find that A is negative at the end, we can negate it and get the right area.
We note that this is just a special case of the simple algorithm for computing polygon areas in general. However, isn't the pictures nice, in the special form of integer grids and axis-parallel edges?
(ii). Computing the area of the polygon plus the pockets
The polygon plus the pockets gives staircases in four (NE, NW, SE, SW) directions. A formal proof would be tedious. A picture with a good example should suffice.
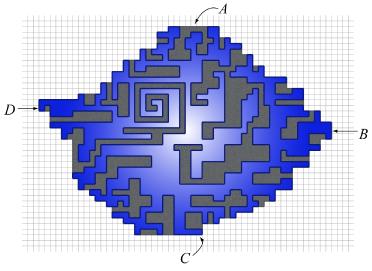
As in the picture, let A be any one of the topmost edges, C be the bottommost
edge, B the right-most, and D the left-most one. We have 4 staircases: one
from A to B, one from B to C, one from C to D, and one from D to A.
Theoretically speaking, these are formed by the maximal points with respect to
four directions, and each of these staircases can be computed in
t(x) := the topmost polygon edge to cross the strip.
b(x) := the bottommost polygon edge to cross the strip.
H(x) := the topmost polygon edge or pocket on that strip.
L(x) := the bottommost polygon edge or pocket on that strip.
For x between A and B, H(x) is the maximum t(x') for all x' between x and B.
We may compute H(x) as follows
H(x) = t(x) for the last strip for x = (the second last strip) down to A H(x) = max(H(x+1), t(x))
The values on the other staircases can be computed in the same manner.
On strip x, the polygon plus pockets are the unit squares between L(x) and
H(x). So we can sum
(iii). Solve our problem
(ii) minus (i).
Analysis — B. Portal
The challenge in this problem was mainly coding a bug-free solution. It was pretty obvious that solving it involved using a shortest path algorithm. And as you can see, even some people in the top 20 skipped this problem to go for other ones, which were more difficult to figure out, but easier to code.
Let's look at bmerry's solution, because it is very readable, and he was the winner of this round. Then I will continue with some other, more efficient solutions.
A state of the game corresponds to the position of the player in the maze and the positions of the two portals, if they exist. This solution considers the map of the maze indexed from 1 so the values (0, 0) for the coordinates of the portals mean that the portals do not exist.
At each step, the player can create a new portal, move one step North, South, East or West or, if he is currently near a portal, and another portal exists, travel from one portal to the other one. The first type of move can be made instantaneously while the second and third types take one turn.
One optimization step is to find, for each cell, the positions of the portals that can be created from that cell, since you don't want to take O(R + C) every time you need to find the possible moves from a state.
If each move took exactly one turn, then the classic breadth-first search
algorithm could provide us with the answer, but in this graph with two types
of weights for the edges it seems like we need Dijkstra's shortest path
algorithm. In fact, we can still use an algorithm very similar to breadth
first search. The tweak is that instead of adding a new state of the same cost
with the current state at the end of the state queue, we add it at the
beginning. This way the states will be expanded in the order of their costs,
which is exactly what Dijkstra's algorithm does. The complexity of this
algorithm is
Code
Here is bmerry's code, modified slightly and with some additional comments.
struct state {
int r;
int c;
// portal rows
int pr[2];
// portal columns
int pc[2];
};
#define ADDR(state) state.r][state.c] \
[state.pr[0]][state.pc[0]] \
[state.pr[1]][state.pc[1]
static unsigned char prio[16][16][16][16][16][16];
static const int dr[4] = {-1, 0, 1, 0};
static const int dc[4] = {0, -1, 0, 1};
int main() {
int cases;
cin >> cases;
for (int cas = 0; cas < cases; cas++) {
cin >> R >> C;
grid.clear();
grid.resize(R + 2);
state start;
memset(&start, 0, sizeof(start));
grid[0] = string(C + 2, '#');
grid[R + 1] = grid[0];
for (int i = 1; i <= R; i++) {
string line;
cin >> line;
grid[i] = "#" + line + "#";
if (grid[i].find("O") != string::npos) {
start.r = i;
start.c = grid[i].find("O");
grid[i][start.c] = '.';
}
}
memset(prio, 255, sizeof(prio));
prio[ADDR(start)] = 0;
deque<state> q;
q.push_back(start);
int ans = -1;
while (!q.empty()) {
state cur = q.front();
unsigned char pri = prio[ADDR(cur)];
if (grid[cur.r][cur.c] == 'X') {
ans = pri;
break;
}
q.pop_front();
for (int d = 0; d < 4; d++) {
int hr = cur.r;
int hc = cur.c;
do {
hr += dr[d];
hc += dc[d];
} while (grid[hr][hc] != '#');
hr -= dr[d];
hc -= dc[d];
// adding a new portal
for (int p = 0; p < 2; p++) {
state nxt = cur;
nxt.pr[p] = hr;
nxt.pc[p] = hc;
if (prio[ADDR(nxt)] > pri) {
prio[ADDR(nxt)] = pri;
// We push the state at the
// front since adding a portal
// is instantaneous.
q.push_front(nxt);
}
}
}
for (int d = 0; d < 4; d++) {
state nxt = cur;
nxt.r += dr[d];
nxt.c += dc[d];
if (grid[nxt.r][nxt.c] != '#') {
if (prio[ADDR(nxt)] > pri + 1) {
prio[ADDR(nxt)] = pri + 1;
q.push_back(nxt);
}
}
}
if (cur.pr[0] > 0 && cur.pr[1] > 0)
for (int p = 0; p < 2; p++)
if (cur.pr[p] == cur.r &&
cur.pc[p] == cur.c) {
state nxt = cur;
nxt.r = cur.pr[1 - p];
nxt.c = cur.pc[1 - p];
if (prio[ADDR(nxt)] > pri + 1) {
prio[ADDR(nxt)] = pri + 1;
q.push_back(nxt);
}
}
}
printf("Case #%d: ", cas + 1);
if (ans == -1)
printf("THE CAKE IS A LIE\n");
else
printf("%d\n", ans);
}
return 0;
}
The restrictions on the inputs in the problem are small enough so that this solution passes all the tests. There are other, more efficient solutions which we thought of.
Other solutions
It does not make sense to create the starting portal before actually being able to jump through it. This way we can improve the previous solution and get the complexity down to O((R*C)2).
As we have just seen, premature portal creation is the root of complexity, so
let's think now of the destination portal. Once we have created a destination
portal, we need to move as quickly as possible to the nearest wall, create a
starting portal, walk through it and arrive at the destination. So what we can
do is just keep R*C states and move from one to another by either going North,
West, South or East or do a teleport move which takes a few turns. We can
compute in O(R*C) how much time each teleport move takes by doing a breadth
first search starting from all the cells in the maze where a portal can be
created. Now we can use Dijkstra's algorithm to find the shortest path. The
final algorithm can have either
More Information
Dijkstra's algorithm - Breadth First Search
Analysis — C. No Cheating
Programming contests have certainly changed over the years. Nowadays, dynamic programming is a trivial matter to many, and bipartite matching is no longer a secret idea. More than half of the contestants solved the small datasets of this problem, and 77 passed the large tests.
Small dataset (Test set 1 - Visible)
The small tests can be solved using dynamic programming. The main idea is to do this row by row.
The naive dynamic programming has states (R1, r), where r is the row number and R1 is the possible configurations of the current row. In order to compute the value of (R1, r), (the maximum number of students who can be put in the first r rows, with the r-th row identical to R1), one can loop through all of the possible values of R2 and use the value of (R2, r-1).
A more sophisticated approach also goes row by row, but in each row, we do it
by squares. The states are (S, r, c), where (r, c) is the current position,
and S is the bitmap for up to n positions before (r, c). These are all the
squares to the left on the same row, and all the squares from the
One may estimate the number of states to be
Large dataset (Test set 2 - Hidden)
Well, but universities do have very large classrooms. The large dataset has tests with 80 rows and 80 columns.
The key idea is to see through the puzzle and notice that this is a standard graph problem. Let each square be a node. What the problem requires is to pick a set of nodes, such that some pairs of nodes cannot be picked together. Let us draw an edge between each such pair of nodes. This is the well-known problem of finding a maximum independent set of the graph. While the general independent set problem is NP-hard, we do know that the problem is tractable on bipartite graphs. A-ha! The graph is indeed bipartite, because all of the edges are between a square in odd-numbered columns and squares in even-numbered columns.
We can easily find the
maximum matching
on bipartite graphs. Let's see how a maximum matching can help us solve the
problem. Let's assume that the size of the matching is X, and the
number of nodes in the graph is N. Notice that the the maximum
independent set cannot contain more than
In general, we have the following relations between the important graph
parameters. For a graph
-
The complement of an independent set is a vertex cover, and vice versa. So
α(G) + μ(G) = |V|. -
To cover all the edges, we need one vertex from any edge of a matching. So
μ(G) ≥ m(G) . -
If G is bipartite, then
μ(G) = m(G) . Equivalently,α(G) + m(G) = |V| .
The last fact can be proved directly, or as a consequence of Hall's theorem, or as an application of the powerful max-flow-min-cut theorem. Below we provide a constructive proof that suits to our problem.
Proof
We will prove that
We have proved that in any bipartite graph, the size of the maximum independent set equals the size of the graph minus the size of the maximum matching.
Code
We believe that many contestants have the standard bipartite matching algorithm prepared. You may download many nice samples from the scoreboard. Below we show a sample solution which keeps the bipartite graph only in mind, and actually runs the matching algorithm on the board itself. From the judges:
int C, N, M;
string bd[100];
int nbx[100][100], nby[100][100], v[100][100];
int T=0;
bool dfs(int a, int b) {
if (a<0) return true;
if(v[a][b]==T) return false;
v[a][b]=T;
for (int i=a-1;i<=a+1;i++)
for (int j=b-1;j<=b+1;j+=2)
if (i>=0 && i<M && j>=0 && j<N && bd[i][j]=='.') {
if (dfs(nbx[i][j], nby[i][j])) {
nbx[i][j]=a; nby[i][j]=b;
nbx[a][b]=i; nby[a][b]=j;
return true;
}
}
return false;
}
int play() {
memset(nbx,-1,sizeof(nbx));
memset(nby,-1,sizeof(nby));
memset(v, -1, sizeof(v)); T=-1;
int rst=0;
for(int i=0;i<M;i++) for(int j=0;j<N;j++) {
if (bd[i][j]=='.') {
rst++;
if (j%2) {
T++;
if (dfs(i,j)) rst--;
}
}
}
return rst;
}
int main() {
cin>>C;
for (int i=1; i<=C; i++) {
cin>>M>>N;
for (int r=0;r<M;r++) cin>>bd[r];
cout<<"Case #"<<i<<": "<<play()<<endl;
}
return 0;
}
More Information
Maximum independent set - Bipartite Matching
Analysis — D. Endless Knight
The small dataset can be solved by simple, two-dimensional dynamic programming. In fact, this is obviously the easiest dataset most of the contestants found in this round, with 884 correct submissions. Quite on the contrary, the large dataset turns out to be the most difficulty for this round, solved by only 32 contestants.
Below we outline three tricks one may use in this problem.
Section A. A nice simplification
Most people are familiar with lattice walks from (0, 0) to (m, n), where each step one can either increase row by 1 or increase column by 1. The total number of such walks is the binomial number (m+n) choose n. One simple reason is that the set of paths is bijective to the ways you choose m steps for vertical moves among the (m+n) steps.
If there are no rocks, one can see that the situation in this problem is quite similar. In fact, they are essentially the same. After a nice transformation of the input, we can forget about the knight and focus on the normal lattice walks.
In our problem, the two kinds of moves the knight can make correspond to the
vectors
r' (2, 1) + c' (1, 2) = (r, c) - (1, 1).
Solving, we get r+c = 2 mod 3, and
r' = r - 1 - (r+c-2)/3, and c' = c - 1 - (r+c-2)/3.
We illustrate using the following picture.
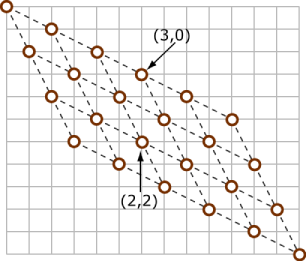
When reading the input, we can transform the points to the new system, and throw away any points that are not reachable. Assume the destination is reachable, otherwise we can simply output 0. We can also disregard any rock with row number or column number that exceeds the destination. In short, we are now in a rectangular lattice in the new coordinate system.
Section B. A key idea
Notice that there is an important restriction in our problem: there are at most 10 rocks. The key idea to our solution -- although other solutions are possible as well -- is the inclusion-exclusion principle.
Let S be any subset of rocks (including the empty set). Define f(S) to be the number of ways we can walk from the origin to destination and hitting every rock in S, and possibly hitting some other rocks.
Number of paths that do not hit any rock = ΣS f(S) (-1)|S|.
Also note: we refer to the Round 1C problem Ugly Numbers. There we needed to consider the multiples of 2, 3, 5, and 7. Some solutions can be viewed as an application of the inclusion-exclusion principle, although this is not necessary for solving that problem.
Section C. N choose K mod 10007?
Now we need to calculate f(S) for any S. Let's sort rocks in S from left to
right, and for rocks on the same column, pick the higher one first. It should
be clear that if some later rock is higher than some earlier ones, then f(S) =
0 -- there is no way to hit all the rocks in S.
Otherwise, the sorted set S forms a chain from the top-left corner to the
lower-right corner
(0, 0) =: (r0, c0) → (r1, c1) → ... → (rk+1, ck+1) := destination
We can view any path hitting all the k rocks as (k+1) stages. f(S) is the product of the number of ways we can do each stage. (This is another important counting principle. It is so important and obvious that usually people don't call it by name. But it does have a name -- the multiplication rule.)
Now, we are back to the classical problem in the beginning of this analysis.
Let
So, is this the end of the story? Not yet. Many contestants failed this
problem because it is tricky to compute A choose B mod 10007 quickly and
correctly. In this problem, both A and B can be on the order of
108. To compute A choose B mod P for a prime number P, one needs
some tricks. There are many clever ways you can find, like pre-computing N!
for all N, pre-computing the inverse of each number mod P, utilizing the
periodicity of the numbers in factorials.
What we want to introduce below is a nice theorem that is not as well known as
it should be. It removes all the worries about the multiples of P. It is not a
difficult theorem, but looks very cute and especially useful for this problem.
Lucas' Theorem: Suppose (ntnt-1...n0) and (ktkt-1...k0) are the representation of n and k in base P, where P is a prime number. Then (n choose k) is the product of (ni choose ki) in ZP.
The following is the choose function from Reid's beautiful Haskel code.
choose :: Int -> Int -> Int10007
choose n k | k > n = 0
choose n k | n < 10007 =
product [ (fromIntegral i) :: Int10007 | i <- [n-k+1..n] ]
/ product [ (fromIntegral i) :: Int10007 | i <- [1..k] ]
choose n k = choose qn qk * choose rn rk
where (qn, rn) = n $$$\mathbf{divMod}$$$ 10007
(qk, rk) = k $$$\mathbf{divMod}$$$ 10007
More information
The inclusion-exclusion principle -
Lucas' Theorem -
Staircase walk
For the study of lattice points, we refer to any standard text in Discrete
Geometry.