Google Code Jam Archive — Round 2 2008 problems
Overview
This was another exciting round with four cute problems.
- A: An easy exercise in dynamic programming.
- B: A puzzle in 2d geometry.
- C: A problem with a beautiful picture in 3d geometry... but the judges overlooked a step in the solution.
- D: A standard dynamic programming on graphs hidden behind a clever reduction.
This round caused some minor trouble for the judges. All four sample solution writers overlooked a key step in the reasoning, and the team had to spend a whole evening rejudging the problem. Fortunately, the change did not have a substantial effect on the list of advancers. This is the only time this year when we had an error in the judges' solutions, and we dodged the bullet. We hope to have zero mistakes in the future!
Thanks to all the participants, especially neal.wu, who first suspected that we had an error and pointed it out.
Credits
Problem A. Cheating a Boolean Tree Written by Xiaomin Chen. Prepared by Mark Gordon
Problem B. Triangle Areas Written by Petr Mitrichev and Igor Naverniouk. Prepared by Igor Naverniouk and Xiaomin Chen.
Problem C. Star Wars Written by Cosmin Negruseri. Prepared by the Code Jam team.
Problem D. PermRLE Written by Petr Mitrichev. Prepared Mark Gordon.
Contest analysis presented by Xiaomin Chen and Cosmin Negruseri.
A. Cheating a Boolean Tree
Problem
For this problem we will consider a type of binary tree that we will call a boolean tree. In this tree, every row is completely filled, except possibly the last (deepest) row, and the nodes in the last row are as far to the left as possible. Additionally, every node in the tree will either have 0 or 2 children.
What makes a boolean tree special is that each node has a boolean value associated with it, 1 or 0. In addition, each interior node has either an "AND" or an "OR" gate associated with it. The value of an "AND" gate node is given by the logical AND of its two children's values. The value of an "OR" gate likewise is given by the logical OR of its two children's values. The value of all of the leaf nodes will be given as input so that the value of all nodes can be calculated up the tree.
The root of the tree is of particular interest to us. We would really like for the root to have the value V, either 1 or 0. Unfortunately, this may not be the value the root actually has. Luckily for us, we can cheat and change the type of gate for some of the nodes; we can change an AND gate to an OR gate or an OR gate to an AND gate.
Given a description of a boolean tree and what gates can be changed, find the minimum number of gates that need to be changed to make the value of the root node V. If this is impossible, output "IMPOSSIBLE" (quotes for clarity).
Input
The first line of the input file contains the number of cases, N. N test cases follow.
Each case begins with M and V. M represents the number of nodes in the tree and will be odd to ensure all nodes have 0 or 2 children. V is the desired value for the root node, 0 or 1.
M lines follow describing each of the tree's nodes. The Xth line will describe node X, starting with node 1 on the first line.
The first (M−1)/2 lines describe the interior nodes. Each line contains G and C, each being either 0 or 1. If G is 1 then the gate for this node is an AND gate, otherwise it is an OR gate. If C is 1 then the gate for this node is changeable, otherwise it is not. Interior node X has nodes 2X and 2X+1 as children.
The next (M+1)/2 lines describe the leaf nodes. Each line contains one value I, 0 or 1, the value of the leaf node.
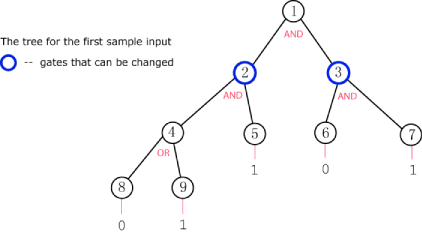
To help visualize, here is a picture of the tree in the first sample input.
Output
For each test case, you should output:
Case #X: Y
where X is the number of the test case and Y is the minimum number of gates that must be changed to make the output of the root node V, or "IMPOSSIBLE" (quotes for clarity) if this is impossible.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
1 < N ≤ 20
Small dataset (Test set 1 - Visible)
2 < M < 30
Large dataset (Test set 2 - Hidden)
2 < M < 10000
Sample
2 9 1 1 0 1 1 1 1 0 0 1 0 1 0 1 5 0 1 1 0 0 1 1 0
Case #1: 1 Case #2: IMPOSSIBLE
In case 1, we can change the gate on node 3 to an OR gate to achieve the
desired result at the root.
In case 2, only the root can be changed but changing it to an OR gate does
not help.
B. Triangle Areas
Problem
Ten-year-old Tangor has just discovered how to compute the area of a triangle. Being a bright boy, he is amazed by how many different ways one can compute the area. He also convinced himself that, if all the points of the triangle have integer coordinates, then the triangle's area is always either an integer or half of an integer! Isn't that nice?
But today Tangor is trying to go in the opposite direction. Instead of taking
a triangle and computing its area, he is taking an integer A and trying
to draw a triangle of area
More precisely, the sheet of graph paper is divided into an
Given the integer A, help Tangor find three integer points on the sheet
of graph paper such that the area of the triangle formed by those points is
exactly
Input
One line containing an integer C, the number of test cases in the input file.
The next C lines will each contain three integers N, M, and A, as described above.
Output
For each test case, output one line. If there is no way to satisfy the condition, output
Case #k: IMPOSSIBLE
where k is the case number, starting from 1. Otherwise, output
Case #k: x1 y1 x2 y2 x3 y3
where k is the case number and (x1, y1), (x2, y2), (x3, y3) are any three integer points on the graph paper that form a triangle of area A/2.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
0 ≤ C ≤ 1000
1 ≤ A ≤ 108
Small dataset (Test set 1 - Visible)
1 ≤ N ≤ 50
1 ≤ M ≤ 50
Large dataset (Test set 2 - Hidden)
1 ≤ N ≤ 10000
1 ≤ M ≤ 10000
Sample
3 1 1 1 1 2 64 10 10 1
Case #1: 0 0 0 1 1 1 Case #2: IMPOSSIBLE Case #3: 1 1 2 3 5 8
C. Star Wars
Problem
Near the planet Mars, in a faraway galaxy eerily similar to our own, there is
a fight to the death between the imperial forces and the rebels. The rebel
army has N ships which we will consider as points
If the cruiser is placed at
(|xi - x| + |yi - y| + |zi - z|) / pi
Your task is to find the position for the cruiser that minimizes the power required for its transmitter, and to output that power.
Input
The first line of input gives the number of cases, T. T test cases follow.
Each test case contains on the first line the integer N, the number of ships in the test case.
N lines follow, each line containing four integer numbers xi, yi, zi and pi, separated by single spaces. These are the coordinates of the i-th ship, and the power of its receiver. There may be more than one ship at the same coordinates.
Output
For each input case, you should output:
Case #X: Y
where X is the number of the test case and Y is the minimal power that is enough to reach all the fleet's ships. Answers with a relative or absolute error of at most 10-6 will be considered correct.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 10
0 ≤ xi, yi, zi
≤ 106
1 ≤ pi ≤ 106
Small dataset (Test set 1 - Visible)
1 ≤ N ≤ 10
Large dataset (Test set 2 - Hidden)
1 ≤ N ≤ 1000
Sample
3 4 0 0 0 1 1 2 0 1 3 4 0 1 2 1 0 1 1 1 1 1 1 3 1 0 0 1 2 1 1 4 3 2 3 2
Case #1: 3.50000000 Case #2: 0.00000000 Case #3: 2.33333333
In the first test case, the four ships have coordinates (0, 0, 0), (1, 2, 0), (3, 4, 0), (2, 1, 0) and powers 1, 1, 1, 1 respectively. We can place a cruiser with the power 3.5 at the coordinates (1.5, 2, 0) which will be able to reach all the ships.
In the second case we can place the cruiser right on top of the ship, with transmitter power 0.
D. PermRLE
Problem
You've invented a slight modification of the run-length encoding (RLE) compression algorithm, called PermRLE.
To compress a string, this algorithm chooses some permutation of integers between 1 and k, applies this permutation to the first k letters of the given string, then to the next block of k letters, and so on. The length of the string must be divisible by k. After permuting all blocks, the new string is compressed using RLE, which is described later.
To apply the given permutation p to a block of k letters means to place the p[1]-th of these letters in the first position, then p[2]-th of these letters in the second position, and so on. For example, applying the permutation {3,1,4,2} to the block "abcd" yields "cadb". Applying it to the longer string "abcdefghijkl" in blocks yields "cadbgehfkilj".
The permuted string is then compressed using run-length encoding. To simplify, we will consider the compressed size of the string to be the number of groups of consecutive equal letters. For example, the compressed size of "aabcaaaa" is 4; the first of the four groups is a group of two letters "a", then two groups "b" and "c" each containing only one letter, and finally a longer group of letters "a".
Obviously, the compressed size may depend on the chosen permutation. Since the goal of compression algorithms is to minimize the size of the compressed text, it is your job to choose the permutation that yields the smallest possible compressed size, and output that size.
Input
The first line of input gives the number of cases, N. N test cases follow.
The first line of each case will contain k. The second line will contain S, the string to be compressed.
Output
For each test case you should output one line containing "Case #X: Y" (quotes for clarity) where X is the number of the test case and Y is the minimum compressed size of S.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
N = 20
S will contain only lowercase letters 'a' through 'z'
The length of S will be divisible by k
Small dataset (Test set 1 - Visible)
2 ≤ k ≤ 5
1 ≤ length of S ≤ 1000
Large dataset (Test set 2 - Hidden)
2 ≤ k ≤ 16
1 ≤ length of S ≤ 50000
Sample
2 4 abcabcabcabc 3 abcabcabcabc
Case #1: 7 Case #2: 12
Analysis — A. Cheating a Boolean Tree
This is an easy exercise in dynamic programming.
Let us define for each node v in the tree,
If v is a leaf with input value 0, then F(v, 0) = 0 -- no gate needs to be
changed; and F(v, 1) can be assigned to -1 or some really big value to
indicate "mission impossible".
If v has two children, u and w, and the gate at v is OR, then F(v, 0) can be
computed by taking the better of the following options.
- Do not change the gate and use the plan for F(u, 0) and F(w, 0);
- Change the gate to AND and use the plan for F(u, 0);
- Change the gate to AND and use the plan for F(w, 0).
So
F(v, 0) = min{ F(u, 0) + F(w, 0), 1 + F(u, 0), 1 + F(w, 0) }.
The other cases are similar. One can compute the F values iteratively bottom-up or recursively top-down.
In addition to the solution above, we introduce some interesting observations.
Look closely at the formula above. Suppose we want the output 0 at the top,
when you start a top-down computation, you will only use values F(_, 0) and
never use any F(_, 1). Similarly, if the desired output at the top is 1, you
will never need to care about the values for F(_, 0). Furthermore, in
computing F(v, 1), you never want to change an OR gate to an AND gate. The
deep reason for these is that, when there is no negation gate involved, the
circuit computes a monotone function, and you will never want to change an
output from 1 to 0 in the middle.
By de Morgan's law, if we interchange all the input values, change all the
gates to the opposite type, and change the desired output from 0 to 1 (or 1 to
0), we obtain a dual problem, and the minimum number of gates one needs to
change remains the same. So we can assume that the desired value is 1 (or 0,
depends on your taste), and forget about implementing half of the cases.
Analysis — B. Triangle Areas
This problem was originally in the form of a little puzzle: For how many numbers is the area possible? The answer is that there are MN such numbers, for any integer 0 < A ≤ MN, we can find a triangle with area A/2 formed by integer points on the graph paper.
The following picture gives the key step in the proof, as well as a solution to our problem.
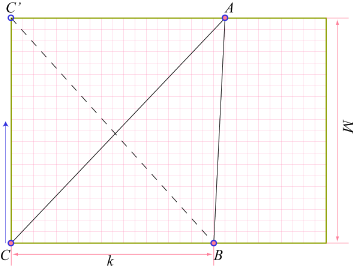
Assume the integer part of A/M is k, we have kM ≤ A ≤ (k+1)M. Denote S(XYZ) the area of triangle ΔXYZ. Clearly 2S(ABC) = kM and 2S(ABC') = (k+1)M. Now take a point C* from your pocket, put it on C, and move it up towards C', one unit at a time. What can we say about the quantity 2S(ABC*)?
- It starts with kM and ends with (k+1)M.
- It is monotone increasing because the distance from C* to AB is monotone.
- It is always an integer.
- The journey takes exactly M steps.
Putting these together, the simple conclusion is that 2S(ABC*) will hit every integer between kM and (k+1)M, including A.
Exercises
(1) For the careful readers, there is one more thing we did not prove yet. There is no way to form a triangle on the graph paper with an area bigger than MN/2. Find a simple reason for this.
(2) We argued that 2S(ABC*) must hit A because it will hit every integer between kM and (k+1)M. Reason directly that, while C* is moving upward, S(ABC*) will increase by 0.5 every time C* moves one unit higher.
Analysis — C. Star Wars
This problem offers a nice excursion into some basic pictures in algebra and geometry, and certainly some programming basics.
The problem is to find the smallest power Y0, such that there is a position where power Y0 is good enough to reach all of the ships. Clearly, any power bigger than Y0 is big enough, while any power smaller than Y0 is not. So, the first step towards the solution is to use the binary search. Reduce the problem of finding the smallest Y to a sequence of easier problems of deciding whether a given Y is big enough. Below we can focus on the decision problem for a given Y instead of the original optimization problem.
For a given Y, we have a requirement that each ship i satisfies
(1) (|xi - x| + |yi - y| + |zi - z|) ≤ piY
Geometrically, this means that the point (x, y, z) for the cruiser must be in the octahedron centered at (xi, yi, zi). Each of the N ships gives one octahedron, and a good position for the cruiser exists if and only if all these N octahedra intersect.
Algebraically, (1) is equivalent to the following set of inequalities (prove it!)
x + y + z ≤ xi + yi + zi + piY x + y + z ≥ xi + yi + zi - piY x + y - z ≤ xi + yi - zi + piY x + y - z ≥ xi + yi - zi - piY x - y + z ≤ xi - yi + zi + piY x - y + z ≥ xi - yi + zi - piY -x + y + z ≤ -xi + yi + zi + piY -x + y + z ≥ -xi + yi + zi - piY
For the geometrically inclined, each octahedron is associated with one of the four directions given by the vectors (1, 1, 1), (1, 1, -1), (1, -1, 1) and (-1, 1, 1). Each pair of inequalities states that the projection (the inner product) of (x, y, z) on a given direction vector must be in a certain range.
Now we have the problem of solving a set of inequalities of the form
A ≤ x + y + z ≤ B C ≤ x + y - z ≤ D E ≤ x - y + z ≤ F G ≤ -x + y + z ≤ H
where A, B, C, D, E, F, G and H are given. In general, this is a linear program. But it is such a trivial one that we do not need to pull out any serious linear programming algorithms.
Certainly, for the solution to exist, we must have A ≤ B, C ≤ D, E ≤ F, and G ≤ H. But these conditions are not enough. The inequalities can be rewritten as
A - x ≤ y + z ≤ B - x G + x ≤ y + z ≤ H + x C - x ≤ y - z ≤ D - x -F + x ≤ y - z ≤ -E + x
As long as y + z and y - z have solutions, we can get y and z. We want to see whether there is an x such that the range [A - x, B - x] intersects [G + x, H + x], and the range [C - x, D - x] intersects [-F + x, -E + x].
It is easy to see that in order for the first two ranges to intersect, we must have
(2) x in [(A - H) / 2, (B - G) / 2].
And for the other two ranges, we must have
(3) x in [(C + E) / 2, (D + F) / 2].
The last step of our solution is simply to decide whether the two intervals in (2) and (3) have a non-empty intersection.
Analysis — D. PermRLE
Section A. The Hamiltonian cycle in a small world
A Hamilton cycle in a graph is a cycle that visits each node exactly once. Given a weighted, directed, complete graph on n nodes, there are (n-1)! distinct Hamiltonian cycles. It is well known that the problem of finding the shortest (or longest) Hamilton cycle is NP-hard. It is also known to many contestants that, for n as small as 20, dynamic programming makes a difference of n*2n vs. n!, which is the difference between a second and an eternity.
Let's have a look at the n*2n DP trick, in case you have not seen it before.
Without loss of generality, we may view node 0 as the start point of the cycle, as well as its end point. For any subset A of the node set V and any node x in A, we define
dp[A][x] := The shortest path that starts from x, visits each point in A exactly once and ends up at node 0. (*)
To clarify, 0 does not necessary belong to A, but we do count the length of the edge from the last point to node 0. Thus the problem of finding the shortest Hamilton cycle is just dp[V][0]. (Convince yourself, maybe looking at (*).)
We need to compute dp[A][x]. For the easy cases where A = {x}, the answer is
just the length of edge x→0. Otherwise, we focus on the first step of the
path. If the first step is x→y, with edge length q, then we pay
- length(x→0), if A = {x}.
- min { dp[A - x][y] + length(x→y) | y in A - x }, if |A|>1.
Section B. Wrap everything into a small world
For any string, define the number of switches to be the number of times adjacent characters are different in the string. We want to find a permutation that transforms S to one S' where the number of switches is minimal. Assume the length of S is mk. Then S can be viewed as a string with m blocks of length k.
Now we introduce a visual aid to simplify our writing. Let us draw the string S as m rows, each block on a single row. The key image is to count the number of switches one column at a time.
Let us take a semi-concrete example. Suppose that at one point we have decided that 5 is permuted to the 7th position, and that 2 goes to the 8th position. Then without knowing the rest of the permutation, we can inspect the 5th and 2nd characters in each block. Suppose that in Z of the blocks the 5th and the 2nd characters are different, then we know that in any such permutation, we will have to pay the price of Z.
The one exception is the last element of the permutation. In all cases but one, we simply wrap around to the beginning because the end of each k-block touches the beginning of the next k-block in the string, except for the last character in the string. We can handle both cases if we fix the last element of the permutation by trying all possibilities.
Next, we reduce our problem to the one in Section A. Suppose we fix T as the last element in the permutation. Define a weighted, directed, complete graph G on k vertices {1, 2, ..., k}. The weight on the edge x→y is
- the number of blocks where the x-th character is different from the y-th character in the same block. (if x ≠ T)
- the number of blocks (excluding the last one) where the x-th character is different from the y-th character in the next block. (if x = T)
It is easy to check that for any permutation, the number of switches is the same as the length of the corresponding Hamiltonian cycle in G.
We have k different choices for T. For each T, finding the shortest Hamilton cycle takes O(2k k) time. The construction of the graph takes O(k2m) = O(k |S|) time for each T; it is also easy to construct in O(k2m) time the graphs for all the T's. The running time of the solution is O(2k k2 + k |S|).