Google Code Jam Archive — Round 1A 2008 problems

In spite of the geometric flavor in the name of this problem, it is truly a story of two arrays.

There are two permutations involved. However, after you fix the permutation for V₁, you have complete freedom in choosing the permutation for V₂. It is clear that the first permutation really does not matter. The important thing is which x_i gets to be matched to which y_j.

To make thinking easier, we may assume that the first permutation has

x1 ≤ x2 ≤ ... ≤ xn. (1)

And our task is to match the y's to the x's so that the scalar product is as small as possible.

At this point, if you need a little exercise in the middle: Think about the case n = 2, and just use a concrete example. What you will surely discover is that, in order to achieve the minimum scalar product, you always want to match the smaller x_i with the bigger y_j.

What we would like to prove is: under condition (1), one of the optimal solutions is of the form

  y1 ≥ y2 ≥ ... ≥ yn. (2)

The rigorous proof of (2) is given at the end of this analysis. For an easy reading, we point out that the key step is really the n = 2 case. If x < x' and y < y', then

(xy + x'y') - (xy' + x'y) = (x - x')(y - y') > 0. (*)

So we prefer to match bigger y's with smaller x's.

Therefore, this problem is solved by the following simple algorithm.

sort(v1.begin(), v1.end());
sort(v2.begin(), v2.end(), greater<int>());
long long ret = 0;
for (int i = 0; i < n; i++)
  ret += (long long)(v1[i]) * v2[i];

Proof of (2). We prove that any permutation that does not satisfy (2) can be transformed into one satisfying (2), and in each step we do not increase the scalar product.
Indeed, any unsorted array can be transformed to a sorted one by only interchanging adjacent elements that are out of order. (For more rigorous readers: prove this, maybe by counting the number of flipped pairs in the array.)
At each step, some x = x_i is matched to some y, and x' = x_i+1 is matched to some y' so that y ≤ y'. We interchange y and y' in this step. The inequality similar to (*), with > replaced by ≥, tells us that the scalar product is not increased in this step. ◊

More information:

The Scalar product

On the surface, this problem appears to require solving the classic problem "Satisfiability," the canonical example of an NP-complete problem. The customers represent clauses, the milkshake flavors represent variables, and malted and unmalted flavors represent whether the variable is negated.

We are not evil enough to have chosen a problem that hard! The restriction that makes this problem easier is that the customers can only like at most one malted flavor (or equivalently, the clauses can only have at most one negated variable.)

Using the following steps, we can quickly find whether a solution exists, and if so, what the solution is.

1. Start with every flavor unmalted and consider the customers one by one.
2. If there is an unsatisfied customer who only likes unmalted flavors, and all those flavors have been made malted, then no solution is possible.
3. If there is an unsatisfied customer who has one favorite malted flavor, then we must make that flavor malted. We do this, then go back to step 2.
4. If there are no unsatisfied customers, then we already have a valid solution and can leave the remaining flavors unmalted.

Notice that whenever we made a flavor malted, we were forced to do so. Therefore, the solution we got must have the minimum possible number of malted flavors.

With clever data structures, the above algorithm can be implemented to run in linear time.

More information:

The Satisfiability problem - Horn clauses

This problem with a simple statement was in fact one of the hardest in Round 1. The input restrictions for the small input were chosen so that straightforward solutions in Java or Python, which have arbitrary-precision numbers, would fail. The trick was calculating √5 to a large enough precision and not using the default double value. It turned out that using the Windows calculator or the UNIX bc tool was enough to solve the small tests as well.

Solving the large tests was a very different problem. The difficulty comes from the fact that √5 is irrational and for n close to 2000000000 you would need a lot of precision and a lot of time if you wanted to use the naive solution.

The key in solving the problem is a mathematical concept called conjugation. In our problem, we simply note that (3 - √5) is a nice conjugate for (3 + √5). Let us define

(1)     α := 3 + √5,   β := 3 - √5,   and X_n := αⁿ + βⁿ.

We first note that X_n is an integer. This can be proved by using the binomial expansion. If you write everything down you'll notice that the irrational terms of the sums cancel each other out.

(2)    

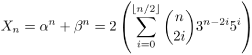
Another observation is that βⁿ < 1, so X_n is actually the first integer greater than αⁿ. Thus we may just focus on computing the last three digits of X.

A side note. In fact, βⁿ tends to 0 so quickly that that our problem would be trivial if we asked for the three digits after the decimal point. For all large values of n they are always 999.

Based on (1) and (2), there are many different solutions for finding the last three digits of X_n.

Solution A. [the interleave of rational and irrational]

One solution goes like this: αⁿ can be written as (a_n + b_n√5), where a_n and b_n are integers. At the same time, βⁿ is exactly (a_n - b_n√5) and X_n = 2a_n. Observe that

(3)     α^{(n + 1)} = (3 + √5)(a_n + b_n√5) = (3a_n + 5b_n) + (3b_n + a_n)√5.

So a_{n + 1} = 3a_n + 5b_n and b_{n + 1} = 3b_n + a_n. This can be written in matrix form as

(4)    

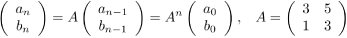
Since α⁰ = 1, we have (a₀, b₀) = (1, 0).

Now we use the standard fast exponentiation to get Aⁿ in O(log n) time. Note that we do all operations modulo 1000 because we just need to return the last three digits of a_n.

Here's some Python code that implements this solution:

def matrix_mult(A, B):
  C = [[0, 0], [0, 0]]
  for i in range(2):
    for j in range(2):
      for k in range(2):
        C[i][k] = (C[i][k] + A[i][j] * B[j][k]) % 1000
  return C

def fast_exponentiation(A, n):
  if n == 1:
    return A
  else:
    if n % 2 == 0:
      A1 = fast_exponentiation(A, n/2)
      return matrix_mult(A1, A1)
    else:
      return matrix_mult(A, fast_exponentiation(A, n - 1))

def solve(n):
  A = [[3, 5], [1, 3]]
  A_n = fast_exponentiation(A, n)
  return (2 * M_n[0][0] + 999) % 1000

Solution B. [the quadratic equation and linear recurrence]

Experienced contestants may notice there is a linear recurrence on the X_i's. Indeed, this is not hard to find -- the conjugation enters the picture again.

Notice that

(5)     α + β = 6, and α β = 4.

So α and β are the two roots of the quadratic equation x² - 6x + 4 = 0. i.e.,

(6)     α² = 6α - 4, and β² = 6β - 4.

Looking at (1) and (6) together, we happily get

(7)     X_n+2 = 6X_n+1 - 4X_n.

Such recurrence can always be written in matrix form. It is somewhat redundant, but it is useful:

From here it is another fast matrix exponentiation. Let us see radeye's perl code that implements this approach here:

sub mul {
    my $a = shift ;
    my $b = shift ;
    my @a = @{$a} ;
    my @b = @{$b} ;
    my @c = ($a[0]*$b[0] + $a[1]*$b[2],
             $a[0]*$b[1] + $a[1]*$b[3],
             $a[2]*$b[0] + $a[3]*$b[2],
             $a[2]*$b[1] + $a[3]*$b[3]) ;
    @c = map { $_ % 1000 } @c ;
    return @c ;
}
sub f {
    my $n = shift ;
    return 2 if $n == 0 ;
    return 6 if $n == 1 ;
    return 28 if $n == 2 ;
    $n -= 2 ;
    my @mat = (0, 1, 996, 6) ;
    my @smat = @mat ;
    while ($n > 0) {
        if ($n & 1) {
            @mat = mul([@mat], [@smat]) ;
        }
        @smat = mul([@smat], [@smat]) ;
        $n >>= 1 ;
    }
    return ($mat[0] * 6 + $mat[1] * 28) % 1000 ;
}
sub ff {
   my $r = shift ;
   $r = ($r + 999) % 1000 ;
   $r = "0" . $r while length($r) < 3 ;
   return $r ;
}
for $c (1..<>) {
    $n = <> ;
    print "Case #$c: ", ff(f($n)), "\n" ;
}

Solution C. [the periodicity of 3 digits]

For this problem, we have another approach based on the recurrence (7). Notice that we only need to focus on the last 3 digits of X_n, which only depends on the last 3 digits of the previous two terms. The numbers eventually become periodic as soon as we have (X_i, X_i+1) and (X_j, X_j+1) with the same last 3 digits, where i < j. It is clear that we will enter a cycle no later than 10⁶ steps. In fact, for this problem, you can write some code and find out that the cycle has the size 100 and starts at the 3rd element in the sequence. So to solve the problem we can just brute force the results for the first 103 numbers and if n is bigger than 103 return the result computed for the number (n - 3) % 100 + 3.

Solution D. [the pure quest of numbers and combinatorics]

Let us see one more solution of different flavor. Here is a solution not as general as the others, but tailored to this problem, and makes one feel we are almost solving this problem by hand.

Let us look again at (2). We want to know X_n mod 1000. We know from the chinese remander theorem that if we can find X_n mod 8 and X_n mod 125, then X_n mod 1000 is uniquely determined.
(a) For n > 2, X_n mod 8 is always 0. Since 5ⁱ ≡ 1 (mod 4), 3^n-2i ≡ 1 or -1 (mod 4) depending on n, so, for n > 2,

(b) To compute X_n mod 125, we only need to worry about i=0,1,2. All the rest are 0 mod 125. In other words, all we need to compute is

There are various ways to compute the elements in the above quantity. The exponents can be computed by fast exponentiation, or using the fact that 3ⁿ mod 125 is periodic with cycle length at most 124. The binomial numbers can be computed using arbitrary precision integers in languages like Java and Python, or with a bit careful programming in languages like C++.

More information:

Binomial numbers - Linear recurrence - Exponentiation - Chinese remainder theorem