Google Code Jam Archive — Qualification Round 2008 problems
Overview
This was the inaugural round for Google Code Jam 2008, and the first real contest run on our own platform! Over 11044 people competed, and 6744 of them solved at least one full problem to advance to Round 1. 576 participants solved all the datasets correctly, including our fun little geometry problem.
We had competitors from 118 different countries, 104 of which had at least one qualifier; India, the United States and China were the top three in participants.
And finally, perhaps the most exciting fact about our qualification round: contestants used over 40 programming languages to solve the problems.
We hope you liked the problems! Congratulations to the people who qualified, and good luck in the remaining rounds!
Credits
Problem A. Saving the Universe Written by Mohamed Eldawy. Prepared by Patrick Nguyen.
Problem B. Train Timetable Written by William Rucklidge. Prepared by Cosmin Negruseri, Ante Derek, and Igor Naverniouk.
Problem C. Fly Swatter Written by Andrew Warner. Prepared by Marius Andrei and Igor Naverniouk.
Contest analysis presented by Cosmin Negruseri and Xiaomin Chen.
A. Saving the Universe
Problem
The urban legend goes that if you go to the Google homepage and search for "Google", the universe will implode. We have a secret to share... It is true! Please don't try it, or tell anyone. All right, maybe not. We are just kidding.
The same is not true for a universe far far away. In that universe, if you search on any search engine for that search engine's name, the universe does implode!
To combat this, people came up with an interesting solution. All queries are pooled together. They are passed to a central system that decides which query goes to which search engine. The central system sends a series of queries to one search engine, and can switch to another at any time. Queries must be processed in the order they're received. The central system must never send a query to a search engine whose name matches the query. In order to reduce costs, the number of switches should be minimized.
Your task is to tell us how many times the central system will have to switch between search engines, assuming that we program it optimally.
Input
The first line of the input file contains the number of cases, N. N test cases follow.
Each case starts with the number S -- the number of search engines. The next S lines each contain the name of a search engine. Each search engine name is no more than one hundred characters long and contains only uppercase letters, lowercase letters, spaces, and numbers. There will not be two search engines with the same name.
The following line contains a number Q -- the number of incoming queries. The next Q lines will each contain a query. Each query will be the name of a search engine in the case.
Output
For each input case, you should output:
Case #X: Ywhere X is the number of the test case and Y is the number of search engine switches. Do not count the initial choice of a search engine as a switch.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
0 < N ≤ 20
Small dataset (Test set 1 - Visible)
2 ≤ S ≤ 10
0 ≤ Q ≤ 100
Large dataset (Test set 2 - Hidden)
2 ≤ S ≤ 100
0 ≤ Q ≤ 1000
Sample
2 5 Yeehaw NSM Dont Ask B9 Googol 10 Yeehaw Yeehaw Googol B9 Googol NSM B9 NSM Dont Ask Googol 5 Yeehaw NSM Dont Ask B9 Googol 7 Googol Dont Ask NSM NSM Yeehaw Yeehaw Googol
Case #1: 1 Case #2: 0
In the first case, one possible solution is to start by using Dont Ask, and
switch to NSM after query number 8.
For the second case, you can use B9, and not need to make any switches.
B. Train Timetable
Problem
A train line has two stations on it, A and B. Trains can take trips from A to B or from B to A multiple times during a day. When a train arrives at B from A (or arrives at A from B), it needs a certain amount of time before it is ready to take the return journey - this is the turnaround time. For example, if a train arrives at 12:00 and the turnaround time is 0 minutes, it can leave immediately, at 12:00.
A train timetable specifies departure and arrival time of all trips between A and B. The train company needs to know how many trains have to start the day at A and B in order to make the timetable work: whenever a train is supposed to leave A or B, there must actually be one there ready to go. There are passing sections on the track, so trains don't necessarily arrive in the same order that they leave. Trains may not travel on trips that do not appear on the schedule.
Input
The first line of input gives the number of cases, N. N test cases follow.Each case contains a number of lines. The first line is the turnaround time, T, in minutes. The next line has two numbers on it, NA and NB. NA is the number of trips from A to B, and NB is the number of trips from B to A. Then there are NA lines giving the details of the trips from A to B.
Each line contains two fields, giving the HH:MM departure and arrival time for that trip. The departure time for each trip will be earlier than the arrival time. All arrivals and departures occur on the same day. The trips may appear in any order - they are not necessarily sorted by time. The hour and minute values are both two digits, zero-padded, and are on a 24-hour clock (00:00 through 23:59).
After these NA lines, there are NB lines giving the departure and arrival times for the trips from B to A.
Output
For each test case, output one line containing "Case #x: " followed by the number of trains that must start at A and the number of trains that must start at B.
Limits
Time limit: 30 seconds per test set.
Memory limit: 1GB.
Small dataset (Test set 1 - Visible)
1 ≤ N ≤ 20
0 ≤ NA, NB ≤ 20
0 ≤ T ≤ 5
Large dataset (Test set 2 - Hidden)
1 ≤ N ≤ 100
0 ≤ NA, NB ≤ 100
0 ≤ T ≤ 60
Sample
2 5 3 2 09:00 12:00 10:00 13:00 11:00 12:30 12:02 15:00 09:00 10:30 2 2 0 09:00 09:01 12:00 12:02
Case #1: 2 2 Case #2: 2 0
C. Fly Swatter
Problem
What are your chances of hitting a fly with a tennis racquet?
To start with, ignore the racquet's handle. Assume the racquet is a perfect ring, of outer radius R and thickness t (so the inner radius of the ring is R−t).
The ring is covered with horizontal and vertical strings. Each string is a cylinder of radius r. Each string is a chord of the ring (a straight line connecting two points of the circle). There is a gap of length g between neighbouring strings. The strings are symmetric with respect to the center of the racquet i.e. there is a pair of strings whose centers meet at the center of the ring.
The fly is a sphere of radius f. Assume that the racquet is moving in a straight line perpendicular to the plane of the ring. Assume also that the fly's center is inside the outer radius of the racquet and is equally likely to be anywhere within that radius. Any overlap between the fly and the racquet (the ring or a string) counts as a hit.
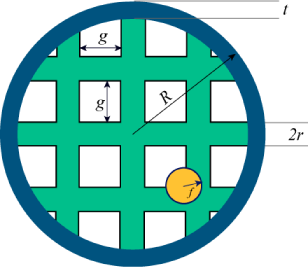
Input
One line containing an integer N, the number of test cases in the input file.
The next N lines will each contain the numbers f, R, t, r and g separated by exactly one space. Also the numbers will have exactly 6 digits after the decimal point.
Output
N lines, each of the form "Case #k: P", where k is the number of the test case and P is the probability of hitting the fly with a piece of the racquet.
Answers with a relative or absolute error of at most 10-6 will be considered correct.
Limits
Time limit: 60 seconds per test set.
Memory limit: 1GB.
f, R, t, r and g will be positive and smaller or equal to 10000.
t < R
f < R
r < R
Small dataset (Test set 1 - Visible)
1 ≤ N ≤ 30
The total number of strings will be at most 60 (so at most 30 in each direction).
Large dataset (Test set 2 - Hidden)
1 ≤ N ≤ 100
The total number of strings will be at most 2000 (so at most 1000 in each direction).
Sample
5 0.250000 1.000000 0.100000 0.010000 0.500000 0.250000 1.000000 0.100000 0.010000 0.900000 0.000010 10000.000000 0.000010 0.000010 1000.000000 0.400000 10000.000000 0.000010 0.000010 700.000000 1.000000 100.000000 1.000000 1.000000 10.000000
Case #1: 1.000000 Case #2: 0.910015 Case #3: 0.000000 Case #4: 0.002371 Case #5: 0.573972
Analysis — A. Saving the Universe
The first task in the new Google Code Jam is about, no surprise, search engines, and also, the grandiose feat of saving the universe in a parsimonious way. However, putting all the fancies aside, the problem itself is easy.
List all queries one by one, and break them up into segments. Each segment will be an interval where we use one search engine, and when we cross from one segment to another we will switch the search engine we use. What can you say about each segment? Well, one thing for sure is:
Never ever ever have all S different search engines appear as queries in one segment. (*)Why is this? Because if all S names appeared in one segment, then any search engine used for that segment will encounter at least one query that is the same as its name, thus exploding the universe!
Working in the opposite direction, (*) is all we need to achieve; as long as you can partition the list of queries into such segments, it corresponds to a plan of saving the universe. You don't even care about which engine is used for one segment; any engine not appearing as a query on that segment will do. However, you might sometimes pick the same engine for two consecutive segments, laughing at yourself when you realize it; why don't I just join the two segments into one? Because your task is to use as few segments as possible, it is obvious that you want to make each segment as long as possible.
This leads to the greedy solution: Starting from the first query, add one query at a time to the current segment until the names of all S search engines have been encountered. Then we continue this process in a new segment until all queries are processed.
Sample code in C++, where st is the set of queries in the current segment, q is the next query, and count is the number of switches.
st.clear();
count = 0;
for (int i=0; i<Q; i++) {
getline(cin, q);
if (st.find(q) == st.end()) {
if (st.size() == S-1) {
st.clear();
count++;
}
st.insert(q);
}
}
If st is a hashset, you expect the solution run in O(n) time. Note that this solution uses the fact that each query will be a search engine name and so we can ignore the list of names provided in the input.
Let us justify that the greedy approach always gives the optimal answer. Think of the procedure as Q steps, and we want to show that, for each i, there is (at least) one optimal choice which agrees with us on the first i steps. We do this inductively for i = 0, then i = 1, and so on. The proposition for i = Q when proven true will imply that our algorithm is correct.
So, the key points in the inductive step i:
- If adding the next query will explode the universe, we must start a new segment. Any optimal choice agrees with us for the first (i-1) steps must also do that.
- If adding the next query will not explode the universe, we do not start a new segment. We know there is an optimal solution R agreed with us for (i-1) steps. Even if in R a new segment is started at step i, we can modify it a little bit. Let R' be the plan that agrees with R, but instead of starting a new segment on the i-th step, we delay this to the (i+1)st. It is clear that R' will also make the universe safe, and has no more switches than R does. So, R' is also an optimal solution, and agrees with our choice for the first i steps.
The similar lines of justifications work for many greedy algorithms, including the well beloved minimum spanning trees.
Analysis — B. Train Timetable
This problem can be solved with a greedy strategy. The simplest way to do this is by scanning through a list of all the trips, sorted by departure time, and keeping track of the set of trains that will be available at each station, and when they will be ready to take a trip.
When we examine a trip, we see if there will be a train ready at the departure station by the departure time. If there is, then we remove that train from the list of available trains. If there is not, then our solution will need one new train added for the departure station. Then we compute when the train taking this trip will be ready at the other station for another trip, and add this train to the set of available trains at the other station. If a train leaves station A at 12:00 and arrives at station B at 13:00, with a 5-minute turnaround time, it will be available for a return journey from B to A at 13:05.
We need to be able to efficiently identify the earliest a train can leave from a station; and update this set of available trains by adding new trains or removing the earliest train. This can be done using a heap data structure for each station.
Sample Python code provided below that solves a test case for this problem:
def SolveCase(case_index, case):
T, (tripsa, tripsb) = case
trips = []
for trip in tripsa:
trips.append([trip[0], trip[1], 0])
for trip in tripsb:
trips.append([trip[0], trip[1], 1])
trips.sort()
start = [0, 0]
trains = [[], []]
for trip in trips:
d = trip[2]
if trains[d] and trains[d][0] <= trip[0]:
# We're using the earliest train available, and
# we have to delete it from this station's trains.
heappop(trains[d])
else:
# No train was available for the current trip,
# so we're adding one.
start[d] += 1
# We add an available train in the arriving station at the
# time of arrival plus the turnaround time.
heappush(trains[1 - d], trip[1] + T)
print "Case #%d: %d %d" % (case_index, start[0], start[1])
Luckily Python has methods that implement the heap data structure operations. This solution takes O(n log n) time, where n is the total number of trips, because at each trip we do at most one insert or one delete operation from the heaps, and heap operations take O(log n) time.
Analysis — C. Fly Swatter
This was the hardest problem of the set, as we can see from the submission statistics, but 652 people succeeded in solving it correctly.
The first step in solving this problem involves a standard trick. Instead of looking for the region that will hit the fly's circular body, we look for the region where the center of the fly must avoid. The problem is thus transformed into an equivalent one where we thicken the size of the racquet to t + f and the radius of the strings from r to r + f. And we consider the fly to be simply a single point, only focusing on its center.
Now the main problem is to find the area of the holes (the areas between the strings, or between the strings and the racquet), and divide it by the area of the disc corresponding to the original racquet. It is easy to see this gives the probability that the racquet does not hit the fly.
A simplifying observation is that we can just look at the first quadrant of the circle, because the racquet is symmetrical.
Now we can go through each square gap in the racquet and check a few cases. Each case consists in computing the area of intersection between the square and the circle representing the inside of the racquet. The case where the square is totally inside or totally outside the circle is easy. The cases left when one corner, two or three corners of the square are inside the circle and the other corners are outside. There are no other cases because we just look at the intersection of a quarter of the circle with small squares.
Each of these cases can be solved by splitting the intersection area into triangles and a circular segment. Here's some code that does this:
double circle_segment(double rad, double th) {
return rad*rad*(th - sin(th))/2;
}
double rad = R-t-f;
double ar = 0.0;
for (double x1 = r+f; x1 < R-t-f; x1 += g+2*r)
for (double y1 = r+f; y1 < R-t-f; y1 += g+2*r) {
double x2 = x1 + g - 2*f;
double y2 = y1 + g - 2*f;
if (x2 <= x1 || y2 <= y1) continue;
if (x1*x1 + y1*y1 >= rad*rad) continue;
if (x2*x2 + y2*y2 <= rad*rad) {
// All points are inside circle.
ar += (x2-x1)*(y2-y1);
} else if (x1*x1 + y2*y2 >= rad*rad &&
x2*x2 + y1*y1 >= rad*rad) {
// Only (x1,y1) inside circle.
ar += circle_segment(rad, acos(x1/rad) - asin(y1/rad)) +
(sqrt(rad*rad - x1*x1)-y1) *
(sqrt(rad*rad - y1*y1)-x1) / 2;
} else if (x1*x1 + y2*y2 >= rad*rad) {
// (x1,y1) and (x2,y1) inside circle.
ar += circle_segment(rad, acos(x1/rad) - acos(x2/rad)) +
(x2-x1) * (sqrt(rad*rad - x1*x1)-y1 +
sqrt(rad*rad - x2*x2)-y1) / 2;
} else if (x2*x2 + y1*y1 >= rad*rad) {
// (x1,y1) and (x1,y2) inside circle.
ar += circle_segment(rad, asin(y2/rad) - asin(y1/rad)) +
(y2-y1) * (sqrt(rad*rad - y1*y1)-x1 +
sqrt(rad*rad - y2*y2)-x1) / 2;
} else {
// All except (x2,y2) inside circle.
ar += circle_segment(rad, asin(y2/rad) - acos(x2/rad)) +
(x2-x1)*(y2-y1) -
(y2-sqrt(rad*rad - x2*x2)) *
(x2-sqrt(rad*rad - y2*y2)) / 2;
}
}
printf("Case #%d: %.6lf\n", prob++, 1.0 - ar / (PI*R*R/4));
This solution takes O(S2) time, where S is the number of vertical strings of the racquet. It's not hard to come up with an O(S) solution because there are at most 4S border squares which can be found efficiently, but the previous solution was fast enough.
Instead of solving the problem exactly, an iterative solution which approximates the area to the needed precision would have also worked. One such solution uses divide and conquer by splitting the square into four smaller squares and then checking the simple cases where the squares are totally inside or totally outside the square. In the cases where the circle and square intersect just recurse if the current square is larger than some chosen precision. An observation is that we can divide every length by the radius of the racquet because it gets canceled in the division between the area of the gaps in the racquet and the disc area. This observation helps the iterative solution since we can make the number of iterations smaller. Here's some sample code:
double intersection(double x1, double y1,
double x2, double y2) {
// the normalized radius is 1
if (x1*x1 + y1*y1 > 1) {
return 0;
}
if (x2*x2 + y2*y2 < 1) {
return (x2-x1) * (y2-y1);
}
// EPS2 = 1e-6 * 1e-6
if ((x2-x1)*(y2-y1) < EPS2) {
// this trick helps in doing 10 or 100 times less
// iterations than we would need to get the same
// precision if we just return 0;
return (x2-x1) * (y2-y1) / 2;
}
double mx = (x1 + x2) / 2;
double my = (y1 + y2) / 2;
return intersection(x1, y1, mx, my) +
intersection(mx, y1, x2, my) +
intersection(x1, my, mx, y2) +
intersection(mx, my, x2, y2);
}